Fórum: PÁLYÁZAT

[1] [2]

Szeretnél hozzászólni? Jelentkezz be.

2004-10-17 13:09:39

B. 3737. megoldása

Azért választottam ezt a feladatot, mert a sorszáma különleges.

A feladat:

Egy konvex négyszög bármely két szemközti oldalára teljesül, hogy az oldalak középpontjai közötti távolság fele a hosszuk összegének. Bizonyítandó, hogy a négyszög rombusz.

Megoldás:

1. ábra: Az ABCD négyszögben $k \le \frac{a+c}{2}$ , ugyanis F₁ F F₃ $\Delta$ oldalai: k, $\frac{a}{2}$ , $\frac{c}{2}$ ( $\frac{a}{2}$ , $\frac{c}{2}$ középvonalak DCB ill. DBA $\Delta$ -ben) Ezt a háromszög-egyenlőtlenség miatt állíthatjuk.

Hasonlóan: $l \le \frac{b+d}{2}$

A feladat szerint: $k=\frac{b+d}{2}$ és $l=\frac{a+c}{2}$

$\frac{b+d}{2}\le \frac{a+c}{2}$ és $\frac{a+c}{2}\le \frac{b+d}{2}$

Ebből következik: $\frac{b+d}{2}= \frac{a+c}{2}$ $\implies$ k= l

2. ábra: A feladat állításából: $k=\frac{a+c}{2}$ $\rightarrow$ a és c oldal fölé emelt Thálész-körök k középvonalon érintik egymást az E pontban. E-ből a és c oldal derékszögben látszik. Ilyen érintési pont nyilván csak egy van.

Hasonlóan: az l középvonalon is van egy F pont, melyből b és d oldal derékszögben látszik, és ilyen pont is csak egy van.

3. ábra: A négyszög oldalainak középpontjai mindig parallelogrammát határoznak meg. Ezen parallelogramma átlói a középvonalak. Mivel beláttuk, hogy ezek egyenlő hosszúak, ez a parellelogramma téglalap. A téglalap oldalai párhuzamosak a négyszög átlóival $\rightarrow$ az átlók tehát derékszögben metszik egymást az M pontban.

4. ábra: M pontból a és c oldal derékszögben látszik $\rightarrow$ M pont rajta van k középvonalon

M pontból b és d oldal is derékszögben látszik $\rightarrow$ M pont rajta van l középvonalon

Tehát: M pont a középvonalak metszéspontja

5. ábra: Látható, hogy az átlók szimmetriatengelyei az F₁ F₂ F₃ F₄ téglalapnak, így BD tengelyre F₁ tükörképe: F₂, B tükörképe pedig önmaga, így: F₁B=F₂B, mivel F₁ és F₂ felezőpontok, ezért AB=BC. Hasonlóan: AD=DC és AD=AB $\rightarrow$

Tehát a négyszög rombusz.

[10] lorantfy

2004-10-17 10:06:19

Kedves ScarMan!

Kösz a megoldást! A feladat szövege kimaradt:

C. 741. Szerkesszünk háromszöget, ha adott két oldala, a és b, továbbá tudjuk, hogy (a szokásos jelölésekkel) $\alpha$ =2 $\beta$ .

Előzmény: [9] ScarMan, 2004-10-17 00:25:01

[9] ScarMan

2004-10-17 00:25:01

A C.741 feladatra adott megoldásommal szeretnék részt venni a pályázaton:

Az ábrán látható háromszögben BAC<)=2CBA<)

BAC szögfelezője: AD. ABD háromszög AB oldalán fekvő szögei megegyeznek -> AD=BD:=x ADC háromszög oldalai tehát: b, x, a-x ADC háromszög DAC szöge megegyezik ABC háromszög ABC szögével, a BCA szögben megegyeznek, ezért ADC<)=BAC<), és ADC háromszög hasonló ABC háromszöghöz. Megfelelő oldalaik aránya is megegyezik, ezért:

b/a = (a-x)/b

Mivel a, b adott, a párhuzamos szelők tételét felhasználva meg tudjuk szerkeszteni a-x -et: -vegyünk fel két egy pontból induló félegyenest -egy félegyenesre vegyük fel a és b szakaszt -a másik félegyenesre b szakaszt -a és b végpontjai kössük össze -az összekötő szakasszal párhuzamos szakaszt indítsunk az először felvett b végpontjából, ez kimetszi a-x szakaszt

Ha a szakaszból kimetszünk a-x -et, megkapjuk x-et.

Ezekután ismerjük b-t, x-et, a-x -et, ezekkel meg tudjuk szerkeszteni ACD háromszöget. A CD egyenest meghosszabítva és rámérve a-t, megkapjuk B pontot, így ABC háromszöget.

[8] lorantfy

2004-10-05 22:21:31

Kedves Érdeklődők!

Örömmel tudatom veletek, hogy a TYPOTEX KIADÓ jutalomkönyveket ajánlott fel a PÁLYÁZAT-on résztvevőknek!

Minden résztvevő könyvjutalomban részesül.

Az alább felsorolt könyvek közül választhattok a helyezések sorrendjében.

Azt hiszem érdemes előkeresni egy múlt évi B vagy C megoldást és feltenni ebbe a topikba!

HOLICS László : Versenyfeladatok 3. (1998-2000) Az OKTV Fizikaversenyek feladatai és megoldásai

VERMES Miklós : Az Eötvös-versenyek feladatai 1. (1959-1988)

VANNAY László : Fizikai összefoglaló és példatár

Keith DEVLIN : Matematika: a láthatatlan megjelenítése

LOVÁSZ László - PELIKÁN József - VESZTERGOMBI Katalin :Kombinatorika - az általános és középiskolai matematika szakkörök számára

POGÁTS Ferenc : Varga Tamás matematikai versenyek 1. (1988-1992)

HRASKÓ András (szerkesztő) : Új matematikai mozaik

RÁBAI Imre : Felvételi és próbafelvételi feladatok 1999-2000

ERLICHNÉ BOGDÁN Katalin : Kísérletezz! - Kis fizikusok szakköri munkafüzet

[7] lorantfy

2004-09-30 12:34:28

Kedves Érdeklődők!

A PÁLYÁZAT határidejét meghosszabbítom október 31-ig. Remélem addig érkezik még pár megoldás!

[6] lorantfy

2004-09-26 09:33:07

Kedves Suhanc!

Köszönöm a megoldásodat! Ezzel a feladattal én is sokat vacakoltam, hogy találjak egy "látványos" megoldást. Egyenlőre ott tartunk, hogy alig jön megoldás a pályázatra, nem hogy kizárjuk a Tiédet. Azért összevetem a hivatalos megoldással.

Előzmény: [5] Suhanc, 2004-09-25 20:40:00

[5] Suhanc

2004-09-25 20:40:00

Kedves lászló!

Az alábbi feladatra adott megoldásom szerintem a hivatalostól eltérő, amennyiben azonban a pályázat értékelői ezt máshogy véleményezik, szeretnék elnézést kérni, és jelen megoldásomat a versenyből kizáratni!

B.3665. Adott a síkon tizenhárom pont úgy, hogy közülük bármely öt között van négy, amelyek egy körön vannak. Bizonyítsuk be, hogy az adott pontok közül legalább hat egy körön van.

Megoldás: Tekintsük a 13 pont közül A; B; C pontokat,és egy, az általuk meghatározott körön rajta nem lévő X pontot! Ha ilyen X pont nem létezik, akkor a 12 pont egy körön van tehát készen vagyunk! Ha létezik, a maradék 9 pont legyen D₁;D₂;...D₉! Ekkor egy-egy lépésben tekintsük A;B; C; X; D_i pontokra a feladat állítását! Mivel X nincs rajta ABC háromszög köréírt körén, ezért D_i ABC; ABX; ACX;BCX háromszögek köréírt körei közül az egyiken rajta van, a feladat szövegének megfelelően. Mivel 9 említett D pontunk van, a skatulyaelv értelmében a fent említett négy kör közül lesz olyan, amelyen legalább három D pont van rajta, így összeségében azon a körön legalább hat pont van a fenti 13 pont közül.

Előzmény: [1] lorantfy, 2004-08-27 12:23:10

[4] lorantfy

2004-09-24 11:38:29

Kedves Balázs!

Köszönöm a megoldásodat! Azt hittem már nem lesz pályázó, de megtört a jég! Remélem szeptember végéig érkeznek még megoldások!

Előzmény: [3] Strenner Balázs, 2004-09-23 16:53:29

[3] Strenner Balázs

2004-09-23 16:53:29

B.3711. Az s₁,s₂,...,s₂₀₀₄ nemnegatív valós számok összege 2, továbbá tudjuk, hogy

s₁s₂+s₂s₃+...+s₂₀₀₃s₂₀₀₄+s₂₀₀₄s₁=1.

Határozzuk meg ezen feltételek mellet az S=s₁²+s₂²+...+s₂₀₀₄² kifejezés lehetséges legkisebb és legnagyobb értékét.

Megoldás: Nem megy az általánosság rovására, ha az s_i-k (egyik) legnagyobbikának s₁-et vesszük. Felírhatjuk, hogy

(s₁+s₂+..+s₂₀₀₄)s₁-(s₁s₂+s₂s₃+...+s₂₀₀₃s₂₀₀₄+s₂₀₀₄s₁)=2s₁-1,

ezért

s₁²-s₂s₃+s₃(s₁-s₄)+s₄(s₁-s₅)+...+s₂₀₀₃(s₁-s₂₀₀₄)=2s₁-1.

(1)

s₁ a számok között a legnagyobb, ezért s₁² $\ge$ s₂s₃,és s_i(s₁-s_i+1) $\ge$ 0 és ebből az adódik, hogy (1) jobb oldala is nemnegatív, tehát

2s₁-1 $\ge$ 0,

amiből

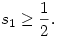$s_1\ge \frac12.$

(2)

(1)-ből adódik, hogy

(s₁-1)²=s₃(s₂+s₄-s₁)-s₄(s₁-s₅)-s₅(s₁-s₆)-...-s₂₀₀₃(s₁-s₂₀₀₄).

(3)

Most tegyük fel hogy s₁ $\ne$ 1, azaz (3) mindkét oldala pozitív. Mivel s_i(s₁-s_i+1) alakú tagok mindegyike nemnegatív, szükséges, hogy s₃(s₂+s₄-s₁)>0 legyen, ami csak akkor lehet, ha

s₂+s₄>s₁

(4)

(3)-at átalakítva kapjuk, hogy

(s₁-1)²=-s₃(s₁-s₂)+s₄(s₃+s₅-s₁)-s₅(s₁-s₆)-...-s₂₀₀₃(s₁-s₂₀₀₄),

(5)

amiből az előbbihez hasonló okoskodással

s₃+s₅>s₁

(6)

adódik. Ilyen átalakítással kapjuk még, hogy

s₆+s₈>s₁

(7).

(4), (6), és (7) felhasználásával kapjuk, hogy

s₁+s₂+s₃+s₄+s₅+s₆+s₈>4s₁ $\ge$ 2,

ami ellentmondás, hiszen 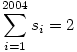$\sum_{i=1}^{2004} s_i=2$ .

Ezek szerint s₁=1, vagyis (3) jobb oldala 0. s₃=0, ugyanis ellenkező esetben s₂+s₄<1, és így s₃(s₂+s₄-s₁)<0, amiből s_i(s₁-s_i+1) $\ge$ 0 miatt az adódik, hogy (3) jobb oldala negatív. Ezzel a gondolatmenettel igazolható (5)-ből, hogy s₄=0, és (3) jobb oldalának további átrendezéséből pedig az, hogy s_i=0, ha i=3,4,5,...,2003.

Innentől már egyszerű a dolgunk, hiszen tudjuk, hogy s₁=1 és s₂+s₂₀₀₄=1, és S=s₁²+s₂²+s₂₀₀₄² maximumát és minimumát keressük.

S=s₁²+s₂²+s₂₀₀₄²=1+(s₂+s₂₀₀₄)²-2s₂s₂₀₀₄=2-2s₂s₂₀₀₄

s₂s₂₀₀₄ minimuma 0, mondjuk s₂=0 esetén, tehát S maximuma 2.

A számtani-mértani közép közti összefüggés szerint

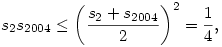
$s_2s_{2004}\le \left(\frac{s_2+s_{2004}}2 \right)^2=\frac14,$

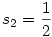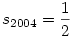ha $s_2=\frac12$ és $s_{2004}=\frac12$ .

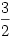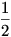Ezek alapján S minimuma $\frac32$ , ekkor az egyik s_i=1, két "szomszédja" $\frac12$ , S maximuma pedig 2, ha két szomszédos s_i értéke 1.

Strenner Balázs 12.o.

Teleki Blanka Gimnázium, Székesfehérvár

[2] lorantfy

2004-09-13 10:09:40

Kedves Érdeklődő!

Tényleg semmi mást nem kell tenned, csak előkeresni egy múlt évi C vagy B megoldásodat és beírni ide a topikba!

[1] lorantfy

2004-08-27 12:23:10

PÁLYÁZAT

1. Pályázhatnak azok az általános és középiskolai diákok, akik az elmúlt tanévben B vagy C pontversenyben vettek részt.

2. A pályázóknak az elmúlt év B vagy C pontversenyének egy saját - a hivatalos megoldásvázlattól eltérő - érdekes megoldását kellene feltennie a Fórum, Pályázat témakörébe.

3. A pályázat kezdődjön a feladat leírásával. A megoldás legyen részletes, diákok számára érthető, áttekinthető formában leírva. A képleteket, matematikai jelöléseket a TeX segítségével kell beírni! Geometriai feladatokhoz ábrát kell mellékelni! A pályamunkákat a többi téma feladataihoz hasonlóan sorszámozzuk!

4. A pályamunkákat a mai naptól 2004. szeptember 30-ig lehet feltenni.

5. Az értékelést a Fórum rendszeres látogatóiból összeálló bírálóbizottság fogja végezni.

6. Díjazás: 1. díj 5000 Ft, 2. díj 3000 Ft, 3. díj 2000 Ft.

7. Egy ember több pályamunkát is feltehet, de csak egy díjban részesülhet, a legjobb munkája alapján

Jó munkát kívánok!

Lorántfy László

[1] [2]

Már regisztráltál?
Új vendég vagy?