Sziasztok! Érdekelne a véleményetek a következő írásról:
A csúcshatás következménye: a nemkonzervatív, nempotenciálos elektromos tér
A könyvekből és a mai tankönyvekből az elektromos tér konzervatív jellege tűnik ki. A következő könyvben is erre az állításra ad példát a szerző. Baranyi Károly: A fizikai gondolkodás iskolája c. könyvében (Akadémiai Kiadó, Budapest, 1992, 2. rész 123. oldal ) az elektromos térerősséget magyarázó példájában egy folyóhoz hasonlítja az elektromos térerősséget, és azt mondja ki, hogy a sűrűsödő erővonalak, melyek az 1.20. ábra alsó részén látható módon jellemzik az elektromos teret, nem származhatnak elektromos állapotú testektől, tehát az elektromos tér csak olyan lehet, ahogy az a 1.20. ábra felső részén látható.(Az erővonalak egymástól egyenlő távolságra helyezkednek el, tehát nem sűrűsödnek; és nem ,ritkulnak.)Az idézet itt olvasható
Érdekes jelenség ebből a szempontból a folyóvíz sebességének a mélységtől való függése. Igen gyakran azt tapasztaljuk, hogy az áramlási sebesség a mélységgel arányosan csökken. Minél mélyebben megyünk a víz felszíne alá, annál kisebb az áramlási sebesség. Ha most egy kis vízalatti járművel leereszkedünk a víz felszíne alá, és a meder közelében a sodrással szemben hajózunk egy bizonyos távolságot, majd felemelkedve egyirányba megyünk a sodrással, akkor ezen a zárt görbén a folyó kis járművünkön pozitív munkát végez. Hasonló a helyzet az 1.20. ábrán látható erőtér esetében. Zárt görbén körbehaladva a tér által végzett munka nem nulla, az egyik szakaszon ugyanis nagyobb az elektromos erő, mint a másik szakaszon. Az ilyen tér - ha van ilyen - nem származhat elektromos állapotú testektől.
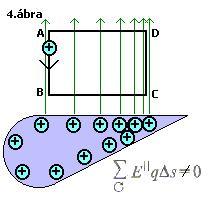
A szerző véleménye szerint az elektrosztatika második alaptörvénye minden elektromos térre érvényes: Az elektrosztatikus térben zárt görbén mozgó q töltésű testen az elektromos tér nulla munkát végez. (1.18.ábra) A tétel kimondása előtt feltették, hogy az elektromos tér jellemzésére szolgáló erővonalak a valóságban nem sűrűsödnek; és nem is ritkulnak, ez esetben a törvény teljesen helytálló. A valóságban azonban ilyen sűrűsödő erővonalakkal rendelkező elektromos térre van példa. Bizonyára közismert jelenség a csúcshatás: Az elektromos töltéssel rendelkező vezető csúcsos (hegyes) részeinél nagyobb az elektromos térerősség (mivel ott nagyobb a töltéssűrűség), mint a vezető többi, csúccsal nem rendelkező részeinél. Ezt a jelenséget mutatja be a 82.2 ábra (Fizika tankönyv 10. osztályosok részére, 82.oldal, Mozaik Kiadó Szeged,2002) Szépen látszanak a sűrűsödő erővonalak. Mozgassunk most végig képzeletben egy pozitív ,q, töltést az ABCD téglalap oldalai mentén (4.ábra). Az ábrán jól látszik, hogy a BC pontok között mozgatva a töltést, az elektromos tér nem végez munkát, ahogy a DA pontok között sem, hiszen az erővonalakra merőlegesen mozog a töltés. Az AB pontok között mozgatva a töltést -E1xq, míg a CD pontok közt mozgatva E2xq erőt fejt ki az elektromos tér. Mivel a megtett út AB és CD esetén ugyanakkora, -E1xqxs=-W1, és E2xqxs=W2, és E2>E1, ezért 0< -W1+W2. Ezért csúccsal rendelkező elektromosan töltött vezetőkre nem érvényes az elektrosztatika második alaptörvénye. Ezt a következő módon is beláthatjuk: ha egy pozitív ,q, töltést az A pontból a C pontba akarunk juttatni, kétféleképpen tehetjük meg: vagy az ABC vagy az ADC útvonalon. Ekkor az elektromos tér által végzett munka függ az útvonaltól (-W1<-W2), tehát a vizsgált elektromos tér nem konzervatív, így nem lehet bevezetni a potenciál fogalmát sem.
Farkas György farkas.gyorgy@free.agria.hu
|