| [1109] Alma | 2012-05-31 16:20:24 |
 Nem úgy értem, hogy a középső kondenzátor fegyverzetén van nulla töltés, hanem azokon a "szigeteken", ahol Lajos bácsi fekete pontjai vannak. A három darab (felső vagy alsó) szigethez kapcsolódó fegyverzet össztöltéséről állítom, hogy nulla.
|
| Előzmény: [1107] Lajos bácsi, 2012-05-31 15:45:34 |
|
|
| [1107] Lajos bácsi | 2012-05-31 15:45:34 |
 "Azt is ki kell használni, hogy a középső csomópontokban 0 az össztöltés"
Miért lenne 0? Ha az alsó és felső ágakban a sorrend egyforma lenne (20,40 és 20,40), akkor elfogadható lenne a 0 érték, de nem így van, tehát mindenképpen jut töltés a C5-re is.
Más szóval két, párhuzamosan kapcsolt, kapacitív feszültségosztó "csuszkája" nem azonos állásban van.
|
| Előzmény: [1106] Gézoo, 2012-05-31 15:31:04 |
|
|
|
| [1104] Alma | 2012-05-31 13:12:22 |
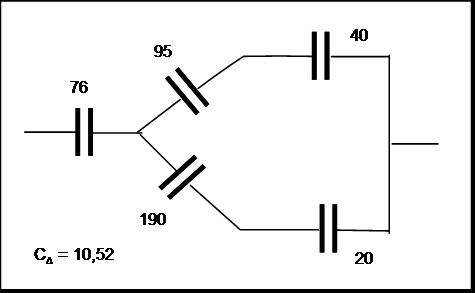
 Nekem kereken C=30uF jött ki. A csillag delta átalakítás egy lehetőség, de tapasztalatom szerint számolásígényesebb más módszereknél. Ha felhasználjuk a C1=C4, C2=C3 egyenlőségeket, akkor szimmetria alapján elég messzire el lehet jutni. Fel kell írni, hogy a rendszer két végén +Q és -Q töltés van, ami valahogy megoszlik a két ág között. Azt is ki kell használni, hogy a középső csomópontokban 0 az össztöltés. Ez alapján egy alkalmas Q1 paraméterrel a C1, C2, C5 kondenzátorok feszültsége rendre Q1/C1, (Q-Q1)/C2 és (Q-2Q1)/C5. Ezek után fel kell írni mondjuk a bal hurokra, hogy a hurokban nincs eredő feszültség (Kirchhoff):
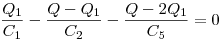
Ebből meghatározod Q1-et, és kiszámolod az egyik ág mentén az összfeszültséget. Ami adódik a kapacitásra:

Érdemes megfontolni a C5=0, C5= , C1=C2 eseteket. Az én képletem mindegyik szélsőséges esetben a várt képletet adja. , C1=C2 eseteket. Az én képletem mindegyik szélsőséges esetben a várt képletet adja.
|
|
| [1103] Gézoo | 2012-05-31 08:38:19 |
 "Én ezt nem merném állítani! "
Azt írtam, hogy "Ránéztéből" ..
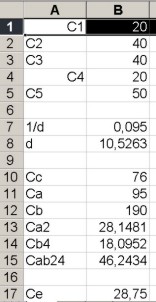
Egyébként valami nem stimmel nálam, mert két eltérő úton is kiszámoltam az eredő kapacitást a C1-C3 közös pontja és a C2-C4 közös pontja között, de nekem ez jött ki:
|
 |
| Előzmény: [1102] Lajos bácsi, 2012-05-31 08:15:14 |
|
| [1102] Lajos bácsi | 2012-05-31 08:15:14 |
 "Vagyis már szemre a baloldali csomópont 1/3 potenciálon van..."
Én ezt nem merném állítani!
A C1<C2, (soros kapcsolásnál csak azonos Q van) ezért Uc1>Uc2, de ez csak az áthidaló ág nélkül igaz.
|
| Előzmény: [1101] Lajos bácsi, 2012-05-31 07:41:43 |
|
| [1101] Lajos bácsi | 2012-05-31 07:41:43 |
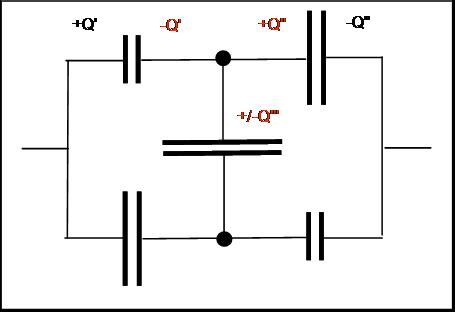
 Töltésmegoszlás áthidaló ággal. (A kondenzátorok rajzjelének nagysága érzékeltetni kívánja a kapacitások arányait, 20,40, 50 uF) Az áthidaló ág töltésének polaritását csak számolás útján lehet meghatározni. A "kucu" összefüggés alapján tudható, ugyanakkora Q töltés esetén, ha nagy az C, akkor kicsi lesz az U.
Csak soros kapcsolásnál a töltések azonosak. Ha tehát 2x nagyobb a kapacitás (40 uF), akkor a feszültség fele lesz a másikénak. Ez az alsó ágra is igaz.
Az áthidaló ág jelenléte módosítja ezeket a töltéseket, így csak logika alpján nehéz lenne eldönteni az ág polaritását.
Most, hogy tudjuk a kérdező 10.-es. Nem hiszem, hogy ennél többet kellene tudnia.
|
 |
| Előzmény: [1100] Lajos bácsi, 2012-05-31 07:22:54 |
|
|
|
|
|
| [1096] Fálesz Mihály | 2012-05-31 03:34:01 |
 A feladathoz nincs feltétlenül szükség csillag-deltára. Leírom, hogyan lehet egy ilyet kiszámolni egy lineáris egyenletrendszer megoldásával.
Azért, hogy az irányokat ne tévesszük össze, mindegyik kondenzátoron kijelölünk egy "pozitív" irányt, amerre a feszültséget és a töltést mérjük. Nem baj, ha az irányokat nem találjuk el; ha a feszültség a másik irányban van, a feszültség és a töltés is negatív lesz.
Mondjuk a jelen esetben az első négy kondenzátornál a jobbfelé mutató irány, az ötödiken a felfelé mutató irány legyen a "pozitív".
Tegyük fel, hogy a rendszerre U=1V feszültséget kapcsolunk; a feszültségeket (ha tetszik, potenciálokat) mondjuk a balolali ponthoz viszonyítva mérjük. A baloldali pontban tehát 0, a jobboldalon U, a felső pontban U1, az alsón U2. Az egyenletrendszerünkben az ismeretlenek az U1 és az U2.
Az egyes kondenzátorokon a feszültség és a töltés:
| kondenzátor |
feszültség |
töltés |
| 1. |
U1 |
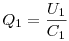 |
| 2. |
1V-U1 |
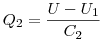 |
| 3. |
U2 |
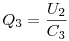 |
| 4. |
1V-U2 |
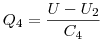 |
| 5. |
U1-U2 |
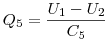 |
|
A felső és az alsó pontok körül a töltések összege nulla, ebből kapsz egy lineáris egyenletrendszert:
+Q1-Q2+Q5=0, +Q3-Q4-Q5=0
Innen már csak nagy levegőt veszel, behelyettesíted, megoldod.
A végén az eredő kapacitás 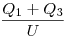 . .
(Remélem, nem írtam el túl sok helyen....)
|
| Előzmény: [1095] bkriszta, 2012-05-30 23:01:18 |
|
| [1095] bkriszta | 2012-05-30 23:01:18 |
 És nem tudnál abban segíteni, hogy hogy kell írnom az adatok alapján egy olyan esetet hogy ez hogyan működik, a töltés hogy oszlik szét és hogyan kell meghatározni az eredő kapacitást. Nagyon köszönöm az eddigi segítséget is, nem is gondoltam volna hogy valaki fog válaszolni. De tényleg csak nagyon alapfeladatokat csinálunk órán, és legkésőbb holnap estig ki kellene számolnom, és nagyon sok az ismeretlen dolog abból, amit leírtatok, viszont nekem ezen múlna az év végi jegyem és fizikás különtanárt is próbáltam keresni,de akit találtam az pont nem ért rá.... Szóval nekem most nagyon fontos lenne a segítségetek!
|
|
| [1094] Gézoo | 2012-05-30 22:38:46 |
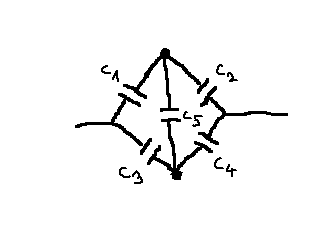
 Az adatokról már ránézésre látszik, hogy keresztben azonosak a kapacitások nagyságai: Felül C1=20 uF, a másik ágon felül C3=40 uF,
alul pedig pont fordítva:
C2=40 uF, és a másik ágon alul C4=20 uF,
Vagyis már szemre a baloldali csomópont 1/3 potenciálon van, a jobboldali pedig 2/3 potenciálon.
Ezt a feltételezést a kapacitív ellenállások segítségével ellenőrizned kellene..
|
| Előzmény: [1092] bkriszta, 2012-05-30 22:28:54 |
|
| [1093] Lajos bácsi | 2012-05-30 22:32:06 |
 A megoldáshoz a csillag-delta átalakításra van szükség. Ezt egy kicsit komplikált lenne itt elmondani. Nézz utána itt.
Egy kis rávezetés: A sorosan kapcsolt kondenzátorok lemezein a töltések azonosak. A közbülső lemezekre - galvanikus kapcsolat nem lévén - csak a villamos megosztás útján válnak szét a töltések. Éppen ezért ezek azonos nagyságúak, és csak az előjelük különböző.
Ha két ilyen ágat kapcsolunk párhozamosan, akkor az ágankénti töltések eltérhetnek. A párhuzamos kapcsolás miatt az ágak feszültsége azonos. A Q=C.U összefüggés alapján belátható, hogy amelyik ágnak nagyobb a kapacitása, annak nagyobb lesz a töltése is.
A Q=C.U összefüggés alapján a C1 és C3 kapacitások feszültsége eltérhetnek.És így tovább.
Mindezeket figyelembe véve különböző értékű kondenzátorok esetén a kérdéses két pont nem lehet ekvipotenciális.
Alakítsd át a C1,C3,C5 delta kapcsolást csillaggá, majd egyesítsd C2 és C4-el, így kezelhetőbb vegyes kapcsolást kapsz. Ezek után már meghatározható a C2 és C4 feszültsége, és ezek ismeretében már számolható valamennyi keresett érték.
|
| Előzmény: [1088] Gézoo, 2012-05-30 21:23:06 |
|
| [1092] bkriszta | 2012-05-30 22:28:54 |
 C1=20mikrofarád=C4, C2=C3=40mikrofarád, C5=50 mikrofarád Az adatokat lefelejtettem..Bocsi
|
|
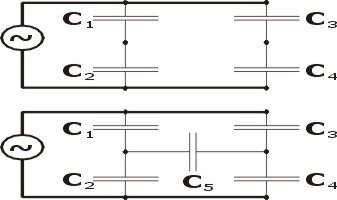
| [1091] Gézoo | 2012-05-30 22:27:37 |
 Azaz a C1C2 ágon a kapacitások aránya adja a közös pontjuk potenciálját akkor is ha egyenfeszültségre kötjük és hagyjuk feltöltődni. Ugyanez igaz a C3C4 ágra is.
A két ág közé tett C5 pedig a két osztáspont közé van kapcsolva.
|
 |
| Előzmény: [1090] Gézoo, 2012-05-30 22:23:33 |
|
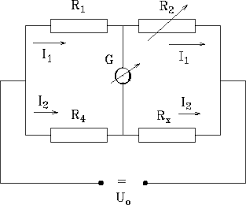
| [1090] Gézoo | 2012-05-30 22:23:33 |
 Az az érzésem, hogy ha egy kicsit másként fogod fel, akkor könnyen megoldhatod, ha észreveszed, hogy ez két-két soros kapacitásból képzett híd.
Azaz ha a bekötnéd egy váltakozó feszültségű forrásra, akkor a kapacitív ellenállás (reaktancia) segítségével, ami a kapacitások nagyságával fordítottan arányos nagyságú:
XC=1/( *C)=1/(2 *C)=1/(2 *f*C) *f*C)
egyszerű feszültség osztót kapnál. (Amit más néven kapacitív Wheastone-hídnak is nevezhetnénk, mert ugyanazon szabályok szerint lehet az osztási arányát számolni.)
|
| Előzmény: [1089] bkriszta, 2012-05-30 21:57:49 |
|
| [1089] bkriszta | 2012-05-30 21:57:49 |
 Az a probléma hogy gimnázium 10. osztályába járok,és heti egy óraszámban, nagyon alapszinten tanuljuk a fizikát, így nem tudom megoldani ezt a szorgalmi feladatot. Szeretném, ha valaki segítene, mert nagyon fontos lenne. Köszönöm (A fizika tanárom azt mondta, hogy neki főiskolás korában egy órát kellet eltöltenie ezzel a feladattal mire rájött a megoldásra.)
|
|
|
| [1087] bkriszta | 2012-05-30 16:36:42 |
 Sziasztok! Már sok mindenkihez fordultam a következő feladattal, de sajnos eddig reménytelenül. Az alábbi ábrán a C5-ös kondenzátor se nem sorosan, se nem párhuzamosan van kapcsolva. A feladat az hogy írni kell egy olyan esetet hogy ez hogyan működik, a töltés hogy oszlik szét és meg kell határozni az eredő kapacitást is. Előre is köszönöm! (jah és elvileg a két pont ekvipotenciális pont)
|
 |
|
|
| [1085] szekibarbi | 2012-05-28 12:43:52 |
 köszönöm mindenkinek a segítséget, pénteken sikeresen 4-re vizsgáztam fizikából!
Nélkületek nem sikerült volna!
Köszönöm!
|
|




 , C1=C2 eseteket. Az én képletem mindegyik szélsőséges esetben a várt képletet adja.
, C1=C2 eseteket. Az én képletem mindegyik szélsőséges esetben a várt képletet adja. 




 *C)=1/(2
*C)=1/(2 *f*C)
*f*C) 