| [358] lorantfy | 2011-06-07 15:33:14 |
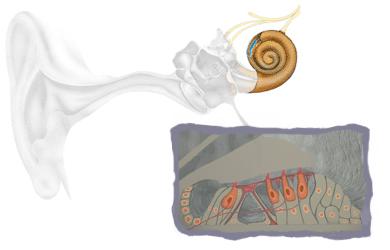
 A belső fülben lévő csiga külső szőrsejtjei hang hatására rezgésbe jönnek. A hallásban ezeknek főleg erősítő szerepük van, de itt az ezek által keltett zajt mérik az un. otoakusztikus emissziós mérés alkalmával. A gyerek fülébe helyezett hangforrás gyors egymásutánban klikkelő hangokat ad és érzékeli a hangokra a belső fülből érkező válaszokat.
Nyilván biztosabb lenne a mérés, ha a csigából az agyba továbbított idegimpulzusokat tudnák mérni. Mágneses magrezonancia mérésekkel már lehetséges az aktív agyterületek vizsgálata, de ez jóval drágább vizsgálat. Ilyen mérésekkel bizonyították, hogy vannak olyan emberek akik hangok hatására színeket is látnak. A beérkező hangok a látásközpont bizonyos részeit is aktiválják.
|
 |
| Előzmény: [357] Zilberbach, 2011-05-19 11:44:22 |
|
| [357] Zilberbach | 2011-05-19 11:44:22 |
 Jó hallású fülben meghatározott paraméterekkel rendelkező zaj keletkezik. Korszerű műszerekkel ezt a zajt mérni lehet - ha a mért zaj nem megfelelő paraméterekkel rendelkezik, akkor a fül hallása nem megfelelő. Így már újszülöttekről is kideríthető, hogy megfelelően hallanak-e. Tudja-e valaki a zaj keletkezésének fizikai részleteit?
|
|
| [356] Zilberbach | 2011-04-03 09:40:48 |
 Ja, és az
"Adott anyag törésmutatója = (fény sebessége vákuumban) : (fény sebessége az adott anyagban)"
definíció meta-anyag esetén nem érvényes.
|
|
| [355] Zilberbach | 2011-04-03 09:34:09 |
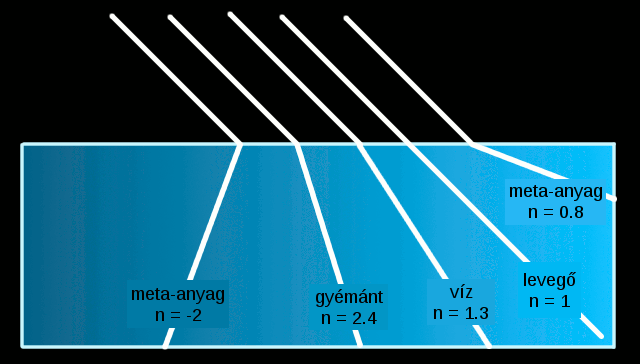
 Elgondolkodva Jonas ábráján: lehet, hogy mégis jó, csak furcsa és szokni kell, illetve magyarázatra szorul.
Ha a pozitív értékű törésmutatók a belépési felületre emelt merőlegeshez tömörödnek exponenciálisan, úgy hogy maga a merőleges megfelel a +végtelen törésmutatónak, akkor jó lehet az ábra.
Továbbá az is furcsa, és szokni kell, hogy a negatív taromány a +végtelen után, és nem a nulla "alatt" kezdődik. Akkor a törésmutató mínusz előjele azt jelzi, hogy a meta-anyag a belépési merőlegesen túlra töri meg a fényt.
A "nulla alatti tartományból" pedig "nem tér meg utazó", vagyis nem értelmezhető, vagy nem létezik.
Talán így van ahogy gondolom, talán nem, ha valaki tudja a választ; írjon. A választ előre is köszönöm.
|
| Előzmény: [351] jonas, 2011-04-02 17:38:03 |
|
| [354] Zilberbach | 2011-04-02 20:44:10 |
 Köszönöm a választ, és az ábrát Jonas.
Az ábrán a számomra zavaró, hogy a mínuszos tartomány a nagyobb számoktól a kisebbek felé haladva, a nullát átlépve szokott következni. Ezen az ábrán viszont a nagyobb pozitív számok felé haladva, egyszercsak megjelenik a mínusz 2 törésmutató.
Már létezik a valóságban olyan meta-anyag, aminek a törésmutatója vörös fényre: mínusz 0,6.
Ez hová kerülne az ábrádon?
A n=-2 és az n=2,4 közé?
Az a meta-anyag viszont, ameyik az ábrádon (+)0,8 törésmutatóval szerepel, már tényleg azt föltételezi, hogy ebben a fény gyorsabban halad, mint a vákuumban.
Tovább haladva ebben az irányban a 0,4 és a még kisebb számok felé, mi következne a nulla után, ha negatív számok tartománya a (+) 2,4 után a nagyobb számok felé haladva jelenik meg?
Szóval szerintem az ábra javításra szorulna.
Számomra még mindíg nem világos, hogy ebben a már létező, mínusz 0,6 törésmutatójú meta-anyagban hogyan terjed a fény, mi az oka, hogy negatív előjelű, és egynél kisebb törésmutatóval kell jellemezni.
|
| Előzmény: [353] jonas, 2011-04-02 18:36:09 |
|
| [353] jonas | 2011-04-02 18:36:09 |
 Ez egyszerűbb: egynél nagyobb törésmutatót egyszerűen úgy láthatsz, hogy lemerülsz a víz alá (úszószemüvegben vagy a nélkül), és megnézel egy levegőbuborékot.
|
| Előzmény: [352] Zilberbach, 2011-04-02 17:43:37 |
|
| [352] Zilberbach | 2011-04-02 17:43:37 |
 Problémám van még annak az értelmezésével is, hogy a meta-anyagok törésmutatójának abszolút értéke is kisebb, mint 1. Ez azt sugallja, hogy a meta-anyagokban a fény sebessége nagyobb, mint a vákuumban - ez viszont számos mértékadó fizikus (pl: Einstein) szerint nem lehetséges.
|
|
| [351] jonas | 2011-04-02 17:38:03 |
 A törésmutatót sebességként elképzelni azért nagyon szemléletes, mert a közönséges esetben mondhatjuk azt, hogy két pont között a fény a lehető leggyorsabban akar eljutni, ezért változtat irányt a törésmutatóknak megfelelően. Attól, hogy ez az elképzelés negatív törésmutató esetén nem működik, még tekintheted a törésmutatót egyszerűen egy olyan számnak, ami megmondja, hogyan változtat irányt a fény. Hogy a törésmutatónak ilyenkor mi is a sebesség jellegő jelentése, és hogy létezik-e ilyen anyag, azt majd a fizikusok elmagyarázzák. Ennek ellenére, még ha a fizikusok erre nem is tudnának jó magyarázatot adni, ki lehetne gondolni negatív törésmutatójú anyagokat, és el lehetne képzelni, hogy törné a fényt egy ilyen anyag: ilyenkor sem a fizikai megvalósítással, sem semmilyen sebességgel nem kell foglalkozni.
|
 |
| Előzmény: [350] Zilberbach, 2011-04-02 15:00:29 |
|
| [350] Zilberbach | 2011-04-02 15:00:29 |
 Adott anyag törésmutatója = (fény sebessége vákuumban) : (fény sebessége az adott anyagban)
Fönti definíció alapján nem tudom értelmezni, mit jelent, ha egy anyag törésmutatója negatív szám.
Első gondolatom az lenne, hogy az adott anyagban a fény terjedési iránya az ellenkezőjére változik, és ennek a jele a negativ előjel a törésmutató előtt. A meta-anyagokban nincs szó erről. De akkor mi a fizikai tartalma a meta-anyagok negatív előjelű törésmutatójának?
|
|
| [349] SmallPotato | 2011-04-01 22:46:49 |
 Vannak erre jó kis vektorábrák, de a neten nem akadtam rájuk.
Itt azért van némi segítség a dologhoz. A legalsó ábrát nézd. A tervezett menetirány a hajó állásából látható; a szél "északról" fúj. Figyeld meg, hogy a vitorlát és a kormánylapátot is a menetirány és a szélirány függvényében állítják be, és gondold át, hogy mikor milyen irányú lesz a hajóra ható eredő erő.
|
| Előzmény: [345] Zilberbach, 2011-03-30 22:19:02 |
|
| [348] Zilberbach | 2011-03-31 23:52:41 |
 Jonas "pontosító" kérdésével komlytalannak tartja az én kérdéseimet.
Ezzel kapcsolatban megfontolásra ajánlanám az alábbi gondolatokat:
1. Szorítsunk össze erősen két ujjunk közé egy nedves meggymagot. A két ujj szorításától eltérő irányban fog "kilőni", nagy sebességgel.
A vitorláshajót a víz fölfelé nyomja, jelentős fölhajtóerővel. A szél egy ettől eltérő irányba szorítja. Elképzelhetőnek tartom, hogy a hajó egy ezektől az erőktől eltérő irányba fog mozogni, a meggymaghoz hasonlóan.
2. A szél súrlódik a vízzel, sebességét ez csökkenti. Ha a hajó súrlódása a vízzel kisebb, mint a szél súrlódása a vízzel, akkor a szél a hajó vitorlái mögött fölgyorsulhat, ezért gyosabban hajthatja a hajót.
|
| Előzmény: [347] jonas, 2011-03-31 17:50:46 |
|
|
| [346] Zilberbach | 2011-03-31 08:54:16 |
 Állítólag olyan vitorlás-hajó is létezik, amelyik 35 km/ó sebességgel fújó hátszélben 45 km/ó sebességgel képes haladni.
Tudja-e valaki ennek a magyarázatát?
|
|
| [345] Zilberbach | 2011-03-30 22:19:02 |
 Több megbízhatónak tűnő helyen is előfordult az információ, hogy vitorlás hajóval lehet széliránnyal szemben haladni.
Tudja-e valaki, ennek a fizikai alapját?
|
|
| [344] Geg | 2011-02-10 12:46:47 |
 Annyiban kiegeszitenem es javitanam is magam, hogy azert nem igaz az, hogy nem lehet hatarsebessegrol beszelni, csak ezt mindig az adott problema meretei szabjak meg. Az mar mas kerdes, hogy ez surlodo gaz eseten nem relevans kerdes, mert belul amugyis ho termelodik, vagyis nem is merulhet fel az, hogy kvazisztatikus adiabatikus -e a folyamat (amiben tehat dS=0). Azonban pont kvazisztatikus esetben igaz csak az, hogy az elemi entropiavaltozas dS= Q/T, altalaban nem. Q/T, altalaban nem.
|
| Előzmény: [343] Geg, 2011-02-10 11:32:54 |
|
| [343] Geg | 2011-02-10 11:32:54 |
 Nem lehet hatarsebessegrol beszelni. Amennyiben a kezdeti allapot es a vegallapot kozott entropiakulonbseg van az utobbi javara, akkor a folyamatot semmi esetre sem lehet kvazisztatikusnak tekinteni, mert ha az lett volna, akkor az entropia nem valtozik. Marpedig ha van belso surlodas, akkor belul ho keletkezett es a gazok entropiaja a 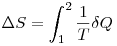 keplet szerint nott. Maskepp mondva: a surlodas altal keltett hot sosem fogjuk (teljes egeszeben) mechanikai munkava visszaalakitani, a folyamat irreverzibilis, amiben az entropia mindig no. keplet szerint nott. Maskepp mondva: a surlodas altal keltett hot sosem fogjuk (teljes egeszeben) mechanikai munkava visszaalakitani, a folyamat irreverzibilis, amiben az entropia mindig no.
|
| Előzmény: [341] patba, 2011-02-10 07:49:03 |
|
|
| [341] patba | 2011-02-10 07:49:03 |
 Nem számoltam ki, de nem hiszem, hogy a fal 20m/s-nál nagyobb sebességgel mozogna bármikor is. Akkor ez már nem tekinthető elég jó közelítéssel kvazisztatikus folyamatnak? Mekkora a határsebesség, aminél még rá lehet mondani, hogy kvazisztatikus?
köszönöm
|
| Előzmény: [337] Geg, 2011-02-10 00:40:00 |
|
| [340] Róbert Gida | 2011-02-10 01:58:09 |
 A feladatok egy másik része meg közönséges lopás. Ha megnézed az informatika részét a Kömalnak, akkor egyszer sem látod azt, hogy "javasolta" xy. Egy-kétszer van csupán, hogy xy OKTV z. feladat ötlete alapján.
Ma már a hasonló programozói oldalak némelyikén ott van egy olyan mező, hogy "resource", azaz forrás. Ha pedig valaki javasol egy példát és üresen hagyja, (azt sem írja oda pl. hogy own resource) akkor jó eséllyel törlik a feladatjavaslatát. A Kömalnál úgy látszik ez nem követelmény.
|
| Előzmény: [339] Geg, 2011-02-10 01:08:32 |
|
| [339] Geg | 2011-02-10 01:08:32 |
 Azert en megvedenem a kituzoket, mert egy ido utan nagyon nehez teljesen uj feladatokat kitalalni, egyszeruen veges sok lehetoseg van a kozepiskolas fizika keretein belul (ami raadasul egyre szukul az evek soran) peldak kituzesere.
Persze egy kis verfrissites sosem arthat, talan lehetne kozepiskolabol nem reg szabadult, lelkes egykori KoMaLozokat talalni, akiknek lennenek uj otleteik feladatokat illetoen. Amugy fizikabol szerintem mostanaban eleg jo peldak szoktak lenni (a matekot nem nezem, ugyhogy nem tudom).
|
| Előzmény: [338] Róbert Gida, 2011-02-10 00:56:20 |
|
| [338] Róbert Gida | 2011-02-10 00:56:20 |
 "Sajnalatos modon a KoMaL-ban is evrol evre felbukkan ez a problema, ami velemenyem szerint rendszeresen felrevezetheti az erdeklodo diaksagot."
Geg ezen nem csodálkoznék, ugyanazok a feladatok pörögnek a Kömalban. Másik topikból Tassy Gergelytől: "Mindkét feladat lényegében szó szerint (nagyon) régi KöMaL-ból való."
Újakat nem nagyon találnak ki a feladatkitűzők, lustaság/trehányság lehet az oka ennek. Szerintem egy Kömal cd-vel a feladatok felének a megoldását ki lehet másolni.
|
| Előzmény: [337] Geg, 2011-02-10 00:40:00 |
|
| [337] Geg | 2011-02-10 00:40:00 |
 A kerdes jogos, a problema feloldasa pedig abban all, hogy a Poisson-egyenleteket csak olyan allapotvaltozasokra szabad alkalmazni, melyekben azon tul, hogy nincs hocsere, "vegtelenul lassuak", un. kvazisztatikus folyamatok. Ezt a kovetelmenyt kozepiskolaban nem hangsulyozzak, sot sokszor nagyon gyors folyamatokat is Poisson egyenletekkel irnak le, ami egesz egyszeruen elvileg hibas. Sajnalatos modon a KoMaL-ban is evrol evre felbukkan ez a problema, ami velemenyem szerint rendszeresen felrevezetheti az erdeklodo diaksagot.
A Poisson egyenletek levezetesekor ugyanis impliciten feltetelezzuk, hogy a gaz allapotanak valtozasa soran mindvegig egyensulyban van, hiszen az elso fotetel differencialis alakjabol indulva, minden egyes idopillanatara alkalmazzuk a pV=NkT allapotegyenletet (integralas utan ebbol jon aztan ki a 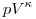 =allando osszefugges). Az allapotegyenlet azonban szigoruan az egyensulyi termodinamika keretein belul ervenyes, nemegyensulyi, gyors folyamatokban nem is ertelmezzuk a gaz nyomasat es homersekletet (legalabbis nem a szokasos modon). =allando osszefugges). Az allapotegyenlet azonban szigoruan az egyensulyi termodinamika keretein belul ervenyes, nemegyensulyi, gyors folyamatokban nem is ertelmezzuk a gaz nyomasat es homersekletet (legalabbis nem a szokasos modon).
A feladatban vazolt folyamatban a Poisson egyenletek ervenyuket vesztik, nem megfordithato (irreverzibilis) allapotvaltozasrol van szo, melyben a masodik fotetel szerint a gaz entropiaja nem marad allando, egeszen az egyensuly bealltaig novekszik. Erre utal a megoldas utolso mondata, mely szerint lengesek jonnek letre, melyet a gaz belso surlodasa allit meg, a fal pedig vegul egy olyan helyen all meg, ahol a nyomasok megegyeznek, a homersekletekre pedig nincs megszoritas. A problema ezzel csupan az, hogy idealis gazzal nem lehet ilyen folyamatot megvalositani, ugyanis az idealis gaz belso surlodasa nulla es a kialakulo lengesek mindorokke fennmaradnak. Ha pedig nem idealis gazzal van dolgunk, akkor nem ervenyes ra a pV=NkT allapotegyenlet, de emiatt viszont a feladat sem elso, sem masodik felere adott numerikus eredmenyeket nem szabad komolyan venni.
|
| Előzmény: [336] patba, 2011-02-09 20:36:28 |
|
| [336] patba | 2011-02-09 20:36:28 |
 De ha tudjuk, hogy adiabatikus, tudjuk a kiinduló állapotokat, akkor egy bizonyos nyomáson csak egy bizonyos térfogatú lehet, nem?
Tehát nem lehet olyan, hogy a nyomás x Pa(itt 3,4.105), és a térfogat vagy y vagy z, hanem a Poisson-egyenletek egyértelműen meghatározzák a térfogatot.
|
| Előzmény: [335] Füge, 2011-02-09 20:32:18 |
|
| [335] Füge | 2011-02-09 20:32:18 |
 Az adiabatikus folyamat azt jelenti, hogy a gáz és a környezet között nem történik hőcsere, azaz Q=0, de ennek semmi köze sincs a hőmérséklet változásnak, ugyanis a hőmérsékletváltozás a belső energia változással, és ebben az esetben a hőtan első főtétele miatt a munkával arányos. Tehát attól, hogy egy folyamat adiabatikus, a gáz hőmérséklete változhat. Mivel a nyomás állandó 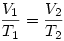 azaz adott nyomáson nem csak egyféle térfogata lehet a gáznak. azaz adott nyomáson nem csak egyféle térfogata lehet a gáznak.
|
| Előzmény: [334] patba, 2011-02-09 20:18:50 |
|
| [334] patba | 2011-02-09 20:18:50 |
 Holics László-A fizika OKTV feladatai és megoldásai 1961-2003 c. könyv 129-130. oldalán levő feladat b) részének a megoldását nem teljesen értem.
Ha az edény fala és a mozgó fal is tökéletes hőszigetelő, akkor a folyamat adiabatikus, azaz a gáz adott nyomáson csak adott térfogatú lehet.
Ám a megoldásnál azt írja, hogy több helyen is megállhat a fal, csupán annak kell teljesülnie, hogy a nyomás ugyanakkora (minden esetben 3,4.105Pa) a tartály két részében. ( =áll. ? ) =áll. ? )
Mi miatt lehet ez az ellentmondás? A feladat megoldója miért nem tekinti adiabatikusnak a folyamatot?
|
|








 Q/T, altalaban nem.
Q/T, altalaban nem.