| [427] Gézoo | 2012-02-29 00:33:54 |
 "Hidd el, eddigi három és fél évnyi egyetemi tanulmányaim alatt olvastam néhány "tankönyvet"." Elhiszem! De sajnos kevés volt. Nagyon kevés.
Ami igaz, az igaz.. Marci I. és Marci II. törvényeket 10 és 12 évesen alkotta meg.
Talán neked sem ártana némi kísérletezés.. de legalább mechanika tárgykörében.
|
| Előzmény: [425] Alma, 2012-02-28 21:48:16 |
|
| [426] Gézoo | 2012-02-29 00:31:00 |
 "Meg tudsz pörgetni egy labdát anélkül, hogy meglöknéd." Természetesen Igen!
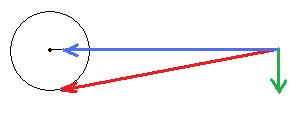
"Az eredő forgatónyomaték és az eredő erő lényegében független egymástól " - Ezt ne terjeszd.. Ha két, egymással ellentétes irányú és egyforma nagyságú erő hatásvonala egyenlő távolságban van a labda forgástengelyétől, akkor a labda forgásba jön. Még pedig a labda tömegét forgásba hozó erők eredője ezúttal a két erő (abszolút értékének) összege.
"A fizika törvényei mást mondanak, ez nem így játszódik le a természetben. Hol találtad? "
Hohó! Ez pedig a kisfiam egyik forgástörvénye.. Marci II. törvénye. A kísérlet: Üveglemezre tegyél egy nagy csapágygolyót, oldalára egy pici mágnest (mondjuk egy régi CD lejátszó lézer optikájából kiemelt neodym mágnest) És lendületpályáról, különböző magasságokról indítva guríts el mellette egy az előzővel azonos méretű csapágygolyót.
Az ábrán látható jelenséget idézed elő: Lendület perdületté alakul közel 100 százalékban (a közdarab hosszának arányában).
""Zárt rendszer impulzusában és a perdületében tárolt energia összege állandó." Ez nem igaz." Oppá.. Na és miért nem?
Na akkor Marci I. törvénye, más néven a Jojó törvény: A lendületben és a perdületben tárolt mozgásmennyiség egyenértékű, ha egyenlő nagyságú, akkor szabad impulzus képezhető.
Példa: Kifeszített rugóval köss össze egy jojóra feltekert zsinórt és a másik oldalról egy testre a tömegközéppontján átmenő egyenesének és a felületének metszéspontjába kötött zsinórt.
A jojó forgásba jön, de tömegközéppontja szinte álló marad, a rugó másik végén a test egyenes vonalú egyenletes sebességű mozgást végez. A két oldal impulzusa azaz lendülete nem egyforma nagyságú.
Ezt a kísérletet elvégezheted úgy is, hogy mindkét oldalt kiskocsira teszed. Ügyelve arra, hogy a két kiskocsi teljes tömege a jojóval ill a tömeggel együtt egyenlő legyen!
""lásd a Boltzman állandót" Nem látom hirtelen a kapcsolatot, kifejtenéd? " Mondjuk Boltzman is megállapította, hogy a perdületben és a lendületben tárolt energiák összege adja a molekulák kinetikai energiájának az összegét.
"A csillagászati példában feltettem, hogy a bolygó tömege elhanyagolható a csillagéhoz képest, mint ahogy szokott lenni. "
Nos, a Jupiter tömege valóban 2,5-szer nagyobb mint az összes többi bolygóé együtt.. Azaz a Nap tömege Csak a bolygók tömegének 748 -szorosa és nem több. Azaz a 0,006 aránytól nehezen tekintettél el, de az rec748=0,001 -tól már eltekintesz? "Ha akarom vemhes, ha akarom nem"? Érdekes szemlélet.
"Olvasd el angol wikipedián a Kepler problem szócikket, ott is megtalálod majd a perdület megmaradását. "
Ne haragudj, picit sem szeretnélek megbántani, de még magyarul sem érted, akkor miért olvasod angolul?
"Ha egy tömegpont időben állandó potenciáltérben mozog, " Ilyen mező nincs.. Igen? "akkor pedig a mozgási és a helyzeti energia összege állandó," - ezt is mondhatjuk, de nem erről beszélünk..
" nem pedig a "perdületében és lendületében" tárolt energia összege." - Nos, igen.. Így nehéz lesz beszélgetnünk. ha össze nem illő témákat keversz össze.
|
| Előzmény: [424] Alma, 2012-02-28 21:40:07 |
|
| [425] Alma | 2012-02-28 21:48:16 |
 Newton III. törvényét köszönöm, ismerem. :)
"Már bocs! De nem kellene Keplert, Newtont esetleg tankönyvet olvasnod mielőtt ilyeneket leírsz?"
Hidd el, eddigi három és fél évnyi egyetemi tanulmányaim alatt olvastam néhány "tankönyvet".
|
| Előzmény: [423] Gézoo, 2012-02-28 20:59:14 |
|
| [424] Alma | 2012-02-28 21:40:07 |
 "A forgató nyomaték ez nem erő és erőkar szorzata?"
Tömegpontoknál igaz. Kiterjedt testeknél nem. Meg tudsz pörgetni egy labdát anélkül, hogy meglöknéd. Az eredő forgatónyomaték és az eredő erő lényegében független egymástól (egyik az erősűrűség térfogatra vett felösszegzése, másik a forgatónyomaték-sűrűségé, ami pedig kiszámolható az általad leírt módon)
http://m.blog.hu/ge/gezoo-vilaga/image/foton2.gif
A fizika törvényei mást mondanak, ez nem így játszódik le a természetben. Hol találtad?
"Zárt rendszer impulzusában és a perdületében tárolt energia összege állandó."
Ez nem igaz. Képzelj el két testet, mely rugóval van összekötve, és megfeszíted a rugót, majd elengeded a testeket. Az energia periodikusan tárolódik a rugó összenyomódásban és a mozgásban úgy, hogy összegük kiadja a kezdeti energiát.
"lásd a Boltzman állandót" Nem látom hirtelen a kapcsolatot, kifejtenéd?
A csillagászati példában feltettem, hogy a bolygó tömege elhanyagolható a csillagéhoz képest, mint ahogy szokott lenni. Olvasd el angol wikipedián a Kepler problem szócikket, ott is megtalálod majd a perdület megmaradását.
Ha egy tömegpont időben állandó potenciáltérben mozog, akkor pedig a mozgási és a helyzeti energia összege állandó, nem pedig a "perdületében és lendületében" tárolt energia összege.
|
| Előzmény: [422] Gézoo, 2012-02-28 20:56:52 |
|
| [423] Gézoo | 2012-02-28 20:59:14 |
 Na egy ellenőrző kérdés:
Igaz-e az, hogy te éppen akkora erővel vonzod magad felé a Földet, mint a Föld tégedet?
Azaz ha pl. ugrasz egyet, akkor a szabadesés alatt éppen akkora erő húzza feléd a Földet, mint téged húz a Föld felé?
|
| Előzmény: [421] Alma, 2012-02-28 17:15:25 |
|
| [422] Gézoo | 2012-02-28 20:56:52 |
 "Nem tudnak "egymásba alakulni". Az egyiket az erő változtatja, a másikat a forgatónyomaték. "
Húúha.. A forgató nyomaték ez nem erő és erőkar szorzata? És nem képződhet erő nélkül lendületből perdület?
Ezt azért nézd meg mielőtt ilyeneket írsz: http://m.blog.hu/ge/gezoo-vilaga/image/foton2.gif
"Zárt rendszer impulzusa és perdülete állandó."
Ezt úgy tanultuk, hogy: "Zárt rendszer impulzusában és a perdületében tárolt energia összege állandó." (lásd a Boltzman állandót.)
"Gondolj bele, ha egy labdát nekigurítasz a falnak, az visszapattan, megváltozik az impulzusa. Ezzel nincs is gond, a labda nem volt egy zárt rendszer. "
Nos, csak irányt vált. De az impulzusának párja a dobáskor a Földre hatott, majd a visszapattanáskor szintén, de az előzővel ellentétes előjellel.
Egyébként ha nem tartozik ide, miért idézted? (rosszul..)
"Ott a csillag körüli perdület állandó. Bár nem hanyagolható el a bolygó és a csillag kölcsönhatása, de a kettő közötti erőnek nincs forgatónyomatéka a csillagra nézve, így az nem tudja változtatni a bolygó perdületét. a Lendületét viszont változtatja."
Már bocs! De nem kellene Keplert, Newtont esetleg tankönyvet olvasnod mielőtt ilyeneket leírsz?
A bolygó keringésében és perdületében, sőt a Csillaggal képzett tömegrendszer összes perdületében és lendületében tárolt energiák összege állandó. Ez kb olyan mozgást okoz, mint egy leejtett tárgy mozgása vákuumban. [ Egyébként, többek között évszakos változású a Föld perdülete.. ( Csaxólok.) ]
"az pedig nem pontosan a tengely középpontja felé mutat." Nos, mint írtam ez két görgővel kiküszöbölhető.. de nem ott a trükk.
|
| Előzmény: [421] Alma, 2012-02-28 17:15:25 |
|
| [421] Alma | 2012-02-28 17:15:25 |
 A lendület és a perdület két eléggé különböző megmaradó mennyiség, nem jó összemosni őket. Nem tudnak "egymásba alakulni". Az egyiket az erő változtatja, a másikat a forgatónyomaték.
Zárt rendszer impulzusa és perdülete állandó. Ez azt jelenti, hogy ha egy rendszert el tudsz keríteni a világ többi részétől, hogy a kölcsönhatás elhanyagolható legyen, akkor az impulzusa és a perdületa megmaradó mennyiségek.
Gondolj bele, ha egy labdát nekigurítasz a falnak, az visszapattan, megváltozik az impulzusa. Ezzel nincs is gond, a labda nem volt egy zárt rendszer.
Sok esetben az a helyzet, hogy egy nem zárt rendszert vizsgálunk, és mégis megmarad az impulzus vagy a perdület. Erre példa a bolygómozgás egy csillag körül. Ott a csillag körüli perdület állandó. Bár nem hanyagolható el a bolygó és a csillag kölcsönhatása, de a kettő közötti erőnek nincs forgatónyomatéka a csillagra nézve, így az nem tudja változtatni a bolygó perdületét. a Lendületét viszont változtatja.
A koris feladatban is az a trükk, hogy a test, melyet fonállal a tengelyhez kötünk, nem alkot zárt rendszert, a fonálon keresztül kölcsön tud hatni a tengellyel, illetve a Földdel. Abban az esetben maradna meg a perdülete, ha a rá ható erők eredőjének nem lenne forgatónyomatéka a tengely középpontjára nézve. Ez nem teljesül, mert az erő fonálirányú, az pedig nem pontosan a tengely középpontja felé mutat.
|
| Előzmény: [420] Gézoo, 2012-02-28 08:29:35 |
|
| [420] Gézoo | 2012-02-28 08:29:35 |
 "Nincs igazad. Az ideális rendszer, amit le akarsz írni, nem létezik. " Oké-oké, bár nem "igazamnak" kellene lennie, és nem azt "akartam" leírni, hogy ideális rendszer van-e..
Szóval, a perdület megmaradás tétele nem teljesül? Olyan is lehet?
Én úgy tanultam, hogy a lendület és a perdület egymásba szabadon átalakítható, mindkettő megmaradó "mennyiség".
A mechanikai veszteségek köre pedig az energia megmaradás témakörébe tartozik. Nem érinti a perdület-lendület megmaradás tételeinek érvényességét.
Rosszul tanultuk?
|
| Előzmény: [419] Alma, 2012-02-27 22:06:16 |
|
| [419] Alma | 2012-02-27 22:06:16 |
 Nincs igazad. Az ideális rendszer, amit le akarsz írni, nem létezik.
Érdemes odáig leegyszerűsíteni a problémát, hogy súrlódásmentesen mozoghat egy tömegpont a síkon úgy, hogy egy fonállal egy hengerpalásthoz rögzítjük, és a fonálra merőlegesen kezdősebességet adunk. A henger sugarával továbbá tarthatunk nullába.
Azért kell a tengely méretét óvatosan kezelni, mert ha nullának veszed, akkor nincs feltekeredés, örökkön örökké ugyanazon a körpályán mozog.
Minél kisebb a tengelyméret, annál kisebb lesz a tangenciális erő. Azt is szem előtt kell viszont tartani, a megtett út (idő) is nő, ami ahhoz szükséges, hogy feltekeredjen a fonál adott mértékben. Gondolj bele, egy kör alatt 2*r* -vel csökken csak a kötél mérete, ami arányos az r tengelysugárral. Ha arra vagy kíváncsi, hogy rögzített L hosszal mikor rövidül meg a fonál hossza, akkor vezető rendben ez C*1/r-rel fog menni. -vel csökken csak a kötél mérete, ami arányos az r tengelysugárral. Ha arra vagy kíváncsi, hogy rögzített L hosszal mikor rövidül meg a fonál hossza, akkor vezető rendben ez C*1/r-rel fog menni.
Így lehetséges az, hogy bár a tangenciális erő elhanyagolhatónak tűnik, de minél elhanyagolhatóbb, annál tovább hat. Az erő is az idő szorzata nem feltétlen tart nullába, és most nem is teszi ezt.
|
| Előzmény: [418] Gézoo, 2012-02-27 21:15:32 |
|
| [418] Gézoo | 2012-02-27 21:15:32 |
 Szuper! van itt élet is!
Nos, nézzük! Kötél indulási hossz 10 m, feltekerő átmérő 0,01 m, Eltérés a tengelyiránytól 0,006 m
A jelölt szög = arctan(0,006/10)=0,034 fok kezdetben feltekerve 1 m-es sugárig: szög= 0,344 fok ( Most tekintsünk el attól, hogy két görgővel a kötélirány tengelyirányú lehetne. ) Azaz a feltekerő tengelynél ható érintő irányú erő a kötélerőnek 0,006 -ad részétől 0,06-ad részéig növekedhet.
Ami olyan kicsiny, hogy ha a megfogó ember tömegétől, a görkori gördülési ellenállásától eltekintünk akkor nyugodtan eltekinthetünk ettől is.
|
| Előzmény: [417] lorantfy, 2012-02-27 20:15:47 |
|
|
| [416] Alma | 2012-02-27 19:25:51 |
 Ez tévedés. A zsinór csak akkor tud feltekeredni, ha véges méretű tengelyt tételezel fel. Ebben az esetben viszont a zsinórban ébredő erőnek lesz forgatónyomatéka. Ez nem hanyagolható el abban a limeszben sem, amikor a tengely átmérője nulla.
|
| Előzmény: [415] Gézoo, 2012-02-27 17:21:26 |
|
| [415] Gézoo | 2012-02-27 17:21:26 |
 Majdnem.. A feltekeredő zsinór esetében a forgástengely a zsinórt feltekerő rúd tengelye, ezért teljesül.
Nem ott a "trükk".
A logaritmikus spirál esetében jobban látszik a titok, ha nem gurítjuk, hanem mondjuk csúzlival lőjük a golyót. Belépéskor csak lendülete van, kilépéskor lendülete és perdülete. Nagy kérdés az, hogy a körívű pályától "befelé és a kifelé" hajló palástok eseteiben hogyan aránylik a perdület és a "maradó" lendület.
|
| Előzmény: [414] Alma, 2012-02-27 16:49:45 |
|
| [414] Alma | 2012-02-27 16:49:45 |
 Na igen, csak sem a logaritmikus spirálon való mozgáskor, sem a feltekeredő zsinór esetében nem teljesül a perdület-megmaradás, hiszen nem centrális az erőd.
|
| Előzmény: [412] Gézoo, 2012-02-27 12:06:01 |
|
| [413] Gézoo | 2012-02-27 15:21:56 |
 Jajj írja már valaki, hogy zsinóros példában a kerületi sebesség állandó a kerület egyre kisebb, és ezért csak a szögsebesség növekszik!
|
| Előzmény: [412] Gézoo, 2012-02-27 12:06:01 |
|
| [412] Gézoo | 2012-02-27 12:06:01 |
 Oké, akkor ugyanez pepitában:
Görkorin állsz és a derékszíjad egy oszlopra feltekert zsinórra van kötve. Egy medicinlabdát elkapsz, amit én a zsinóroddal kijelölt kör érintőjének irányába dobok. Majd amikor feltekeredett a zsinórod egészen rövidre, elengeded a labdát.
A perdület megmaradás tétele szerint ahogy feltekeredik a zsinór és egyre kisebb lesz a mozgásod sugara, egyre nagyobb lesz a kerületi sebességed.
( A könnyebb számolás kedvéért tegyük fel, hogy neked nincs tömeged.)
Így érthető a sebesség növekedés?
|
| Előzmény: [411] Alma, 2012-02-27 11:08:47 |
|
|
| [410] Gézoo | 2012-02-27 08:32:15 |
 Oké lehet, hogy igazad van. Legyen egy elgondolkodtató kérdés:
i impulzusú golyót gurítunk egy logaritmikus spirál nagyobb sugarú oldalára érintőleges irányból. Amikor a golyő kilép a kis sugarú oldalon impulzusa I. ( I>>i )
A kérdés, hogy az I-i különbözethez szükséges energiát honnan vette a golyó?
|
| Előzmény: [409] Alma, 2012-02-27 01:03:58 |
|
| [409] Alma | 2012-02-27 01:03:58 |
 Én sokkal könnyebben ráveszem magam egy gondolkodtató kérdésre való válaszolásra, mint egy teljesen triviális dolog leírására. Lehet, hogy ezért nem kaptál választ.
|
| Előzmény: [408] Gézoo, 2012-02-25 11:07:34 |
|
|
| [407] lorantfy | 2012-02-25 09:42:12 |
 A láda térfogatát könnyen meghatározhatod. Leméred hosszát, szélességét és magasságát, aztán ezeket összeszorzod (feltéve, hogy a láda téglatest alakú). Az ember térfogatát már nehezebb meghatározni, de ha megtöltesz egy elég nagy dézsát vízzel és megkéred az embert, hogy merüljön bele, akkor miután kimászott a dézsából egy ismert térfogatú edénnyel újra teletöltöd a dézsát vízzel. De a [404]-es kérdés megválaszolásához ezekre nincs szükség.
|
| Előzmény: [406] Gézoo, 2012-02-16 10:19:27 |
|
|
|
| [404] Rita0527 | 2012-02-12 13:35:47 |
 Sziasztok! A segítséget előre is köszönöm! A feladat a következő: Egy 40kg tömegű láda és egy 600N súlyú ember közül: mekkora térfogatú víznek egyenlő a tömege a láda, ill. az ember tömegével? Továbbá mekkora térfogatú víznek egyenlő a súlya a láda, ill. az ember súlyával?
|
|
| [403] jonas | 2012-01-28 17:14:05 |
 Jelölje a két test együttes tömegét M=0.7kg; a felső test tömegét m; a két test közti súrlódási együtthatót  =0.4; a rezgés amplitúdóját pedig A. =0.4; a rezgés amplitúdóját pedig A.
A felső test nyilván akkor csúszhat meg a legkönnyebben, amikor a testek gyorsulása a legnagyobb. Ez akkor következik be, amikor a testek szélső helyzetben vannak, tehát amikor a kitérés éppen A. Ilyenkor a rugó DA erővel hat, ezért a gyorsulás nagysága a=DA/M. Ahhoz, hogy a súrlódás megtartsa a felső testet, am nagyságú erővel kell gyorsítania, viszont a súrlódás legfeljebb  mg erőt fejthet ki, tehát akkor nem csúszik meg a felső test, ha am mg erőt fejthet ki, tehát akkor nem csúszik meg a felső test, ha am  mg. Ebbe behelyettesítjük az a-re kapott kifejezést majd rendezzük: mg. Ebbe behelyettesítjük az a-re kapott kifejezést majd rendezzük:
(DA/M)m< mg, mg,
A  Mg/D=0.028m=2.8cm Mg/D=0.028m=2.8cm
|
| Előzmény: [402] Péter123, 2012-01-28 16:52:54 |
|



 -vel csökken csak a kötél mérete, ami arányos az r tengelysugárral. Ha arra vagy kíváncsi, hogy rögzített L hosszal mikor rövidül meg a fonál hossza, akkor vezető rendben ez C*1/r-rel fog menni.
-vel csökken csak a kötél mérete, ami arányos az r tengelysugárral. Ha arra vagy kíváncsi, hogy rögzített L hosszal mikor rövidül meg a fonál hossza, akkor vezető rendben ez C*1/r-rel fog menni. 
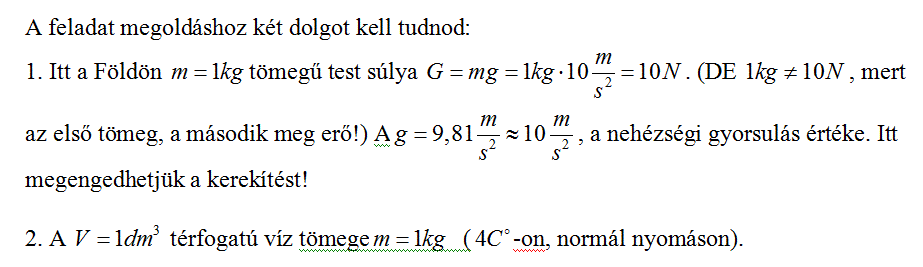

 =0.4; a rezgés amplitúdóját pedig A.
=0.4; a rezgés amplitúdóját pedig A. 