Fórum: Fizikások válaszoljanak

Úgy is 18000,000000000067600000000000381 azaz a különbség delta t= 0,000000000067600000000000381 sec

Használd a Windows tudományos számológépét. A Kellékekben van. Az elég sok tizedesjegyre kiszámolja. A gyököt az INV x2-tel tudod számolni.

Eltérés = 0,000000000067600000000000381 [sec]

t= t0* ß ahol ß=1/gyök(1-v*v/c*c)=1/sin(arc cos(v/c)

t=5*3600/sin(arc cos(26/3e8)=

t=18'000,000000000067600000000000381

(t0= 18'000 sec)

Kedves Mindenki!

A tegnapi heves indulatokat kiváltó feladat más adatokkal... Kérném, ha valaki tud segítsen, mert egyszerűen nem jó a megoldás, és nem tudom, miként lehet kiszámolni!

26 m/s sebességgel megy egy dolgozó a főnökéhez találkozóra. A távolság alapján a főnök kiszámítja, hogy 5 óra szükséges az út megtételéhez. A dolgozó később érkezik és azzal érvel, hogy az autójában lévő GPS pontosan 5 órát regisztrált, a különbség abból adódhat, hogy a mozgó autóban lassabban járt az óra. Mennyi az álló és a mozgó órák eltérése (s-ben)? (c = 3×105 km/s)

Előre is köszönöm!

csak még nem hallottam róla. de köszönöm kedvességed, és udvariasságod, rákeresek, bár nem hiszem, hogy vizsgán használhatom majd ;)

Keress rá (első találat lesz), vagy a google-t sem ismered?

???

"gyök(1-v2/c2)-et számolok, az nálam mindig egy lesz mert olyan kicsi szám jön ki."

WolframAlpha-t véletlenül sem ismered?

Kedves Alma!

köszönöm az egyetlen értelmes választ erre a kérdésre... a gond csak annyi, hogy ha gyök(1-v2/c2)-et számolok, az nálam mindig egy lesz mert olyan kicsi szám jön ki. Úgy viszont nem jó a megoldás... esetleg nem tudnál erre valamilyen megoldást?

[...]

sajnos nem tudom megoldani ezt a feladatot, és őszintén nem is hiszem, hogy valaha használni fogom az életben, szóval elég értelmetlennek gondolom, de mindegy... szóval esetleg valamilyen más/egyéb ötlet? előre is köszönöm :)

(A hozzászólást módosítottam. Moderátor.)

és mellesleg nem a végeredményt szerettem volna megkapni, hanem a leveztetést... mint már mondtam

Tehát nincs eredményed. Neked nem jó az Alma által beírt levezetés végeredménye, nem jó a vele azonos általam beírt transzformáció eredménye..

Na most akkor azt magyarázd el, hogy mitől lenne rossz az általam leírt eredmény? Az is érdekelne, hogy a vele azonos megoldást adó Alma féle függvényt jónak véled?

az van meg, hogy jó e vagy sem... típus feladatok vannak

nem tudom bemásolni, de mindegy, az előbb is írtam, köszönöm, amit eddig írtál, de számomra nem hasznos... csak így tudom bemásolni

34 m/s sebességgel megy egy dolgozó a főnökéhez találkozóra. A távolság alapján a főnök kiszámítja, hogy 8 óra szükséges az út megtételéhez. A dolgozó később érkezik és azzal érvel, hogy az autójában lévő GPS pontosan 8 órát regisztrált, a különbség abból adódhat, hogy a mozgó autóban lassabban járt az óra. Mennyi az álló és a mozgó órák eltérése (s-ben)? (c = 3×105 km/s)

Válasz: Hibás Leadott munka pontjai: 0/2. Ez a leadott munka 2 büntetést kapott.

Nosza akkor ollózd be az eredményt is..

aham... a feladat megoldása megvan... nálad biztosan okosabbak találták ki, mondjuk a tanárom, akinek doktori címe van, nem tudom, talán lehet ő jobban tudja... ellenben nekem a levezetésre lenne szükségem, hogy megérthessem... és hogy én magam is kiszámolhassam.

ja, és képzeld, nem jó amit írsz...

Talán ha látnád.. Kétféleképpen is leírtam a Lorentz transzformálás eredményét.

Amint látom Alma az eredeti függvénnyel ugyanazt, csak be kellene helyettesítened, hogy megkapd a 0,99999999999999357777777777775716-szeres lassulást..

Ha ez neked nem elegendő segítség, akkor már nagy baj van.

Mert helyetted mi már nem tanulhatjuk meg ..

Természetesen a távolságnégyzetet definiáltam, nem a távolságot.

A speciális relativitáselmélet nem csak nagy sebességeken érvényes. Kis sebesség limeszében közelíteni szoktuk, és a közelítés az általunk megszokott elmélet.

Specrelben mindig kiindulhatsz abból, hogy két téridőpont négyestávolsága nem függ a koordinátarendszertől (ha inerciarendszerekre szorítkozunk). Két téridőpont négyestávolsága alatt a következőt értem:

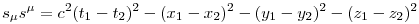
Olyan koordinátarendszerből nézve, melyből x irányú a mozgás a következőt írhatjuk fel a Földhöz rögzített rendszer és a mozgórendszer között (a két téridőesemény az elindulás és a megérkezés):

c²(t₁-t₂)²-(x₁-x₂)²=c²(₁-₂)²

A Földről nézve tudjuk, hogy (x₂-x₁)=v*(t₂-t₁). Ezt behelyettesítve kaphatod a mozgó rendszerben mért időt ("sajátidőt"):

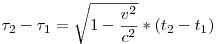
Itt ₂-₁ helyére behelyettesíted a 8 órát, v helyére a sebességet.

itt nem a GPS és a műhold órái közötti különbségen van a hangsúly szerintem... ez egy feladat, és nem az a dolgom, hogy a technikai hátterét elemezzem, hanem hogy megoldjam, feltéve hogy nem akarok megbukni... márpedig nem akarok. de ha nem tudsz segíteni, akkor nem kell, köszönöm, hagyd meg azoknak, akik esetleg tudnak :)

Nézd, itt egy pici elírás is jelentős értelem módosulást okozhat. Például a GPS műholdakon használt órák pontosságával működő óra az autóban már majdnem mérhette volna a főnök órája által mutatottnak a delta = 0,999 999 999 999 993 578 -szorosát.

Csak ott a baj, hogy mint látod a 34 m/s relatív sebességnél csak a 15. tizedesnél van eltérés az órák között. Így a GPS műholdakon használt órák sem eléggé pontosak ahhoz, hogy ilyen pontossággal mérjenek.

A gépkocsiba szerelhető GPS készülékek óráinak a pontossága nagyságrendekkel elmarad a műholdon lévő óra pontosságától.

Így ha valóban beillesztetted az eredeti kiírást, akkor maga a kiírás a hibás.

hát ja, a crtl+c, crlt+v is tévedhet...

Van egy kis félreértés.. Nem csak fénysebességhez közeli sebességek esetében használható a Lorentz transzformáció.

A GPS eszközökben lévő progi eleve az általános relativitás szerint transzformált adatokat írja ki a képernyőjére. Azaz vagy nem a GPS órája szerint 8 óra volt az autóban az út hossza, (amely megegyezik a főnök álló órája szerinti 8 óra időszakasz hosszal, ) vagy a GPS által kiírt .. Több lehetőséget azon kívül nem látok, hogy esetleg harmadik lehetőségként a feladatkiírást pontatlanul idézted.

aham... csakhogy mi a relativisztikus kinematikából kaptuk ezt a feladatot...

szóval hogyan lehet megoldani? mivel a Lorentz transzformáció szerint csak akkor jó a feladat, ha a fénysebességhez közeli értékkel halad az autó. de nem igazán csillagharcos a dolgozó...

valami ötlet?

"Nem mérünk erőt. Teljesen mindegy, milyen kölcsönhatás van a két test között," Ha nem mérünk erőt, akkor a tömeg mozgásállapot változásáért nem feltétlenül a nem mért vagy nem mérhető kölcsönhatás lehet a felelős. Hiszen azt sem tudhatjuk, hogy van-e kölcsönhatás, ha nem mérjük meg a kölcsönhatás nagyságát.

" csak a kölcsönhatás előtti és utáni sebességeket mérjük meg." Bármely rendszerben nyugvó, minden test mozgásállapot változása végtelen sok rendszerből mérhető. Akár van akár nincs kölcsönhatás a megfigyelő és a mozgásállapot változást elszenvedő között.

" Kölcsönhatás közben semmit nem mérünk, nincs szükség arra a tömeg meghatározásához." Ha így tennénk, akkor semmit sem tudnánk meg a tömeg nagyságáról.

Példa: A megfigyelt mozgásállapot változások: a=dv/dt [m/s/s]= 1 ; 10 ; 100; 1000

Mekkora a tömeg?

Ugye nyilvánvalóan nem elegendő az általad leírt mozgásállapot változás a tömeg nagyságának definiálásához.

"A proton és a neutron nem is elemi részecske, jelen tudásunk szerint csak az elektron az három közül. Mellesleg, az elektront pontszerűnek tételezzük fel. Elemi, vagyis nincs belső struktúrája (úgy véljük)."

Az elemi részecske fogalma értelmezés kérdése. Az elektron (holon és spinon), a proton (uud kvarkok) és a neutron (ddu kvarkok) összetevői sem igazoltan elemi részecskék. Atomi (Bohr) szinten pedig mindhármat elemi részecskének tekintjük.

Az pedig, hogy a számítások egyszerűsítése érdekében mit tekinthetünk pontszerűnek, teljesen más kérdés. Például a Földet a 12 millió méteres átmérője ellenére a gravitációs számításokban gyakorta pontszerűnek tekintjük.