| [802] Alma | 2012-05-07 00:07:31 |
 Kedves Gézoo!
Nem, ebben nincs igazad, a "s'=s*sin(arccos(v/c))" képlet nem adja meg az úthossz transzformáltját.
Épp a minap tartottam egy előadást egy ismeretterjesztő egyetemi konferencián, mely témája súrolta a speciális relativitáselméletet, és ott is igyekeztem illusztrálni két téridőesemény térbeli távolságának változását ha áttérünk más koordináta-rendszerre. Következőképp érveltem:
Vegyünk két téridőeseményt: ülünk egy vonaton, a vonat indulása 14:00 Budapest, érkezés 17:00 Pécs. A Földhöz rögzített koordináta-rendszerben az indulás és a megérkezés térbeli távolsága, mint tudjuk, körülbelül 200 km. Nézzük meg ugyanezt a vonathoz rögzített koordináta-rendszerben! Mit látunk onnan? Az utas ül a székén, nem mozdul egész út során, és valahogy mégis eljut Budapestről Pécsre. Abban a koordináta-rendszerben 0 a sebessége, mozgást nem végez. Nincs megtett út. Ebből pedig ugye következik, hogy a vonathoz rögzített koordináta-rendszerben az indulás és érkezés téridőesemények térbeli távolsága 0.
A "s'=s*sin(arccos(v/c))" képlet természetesen nem ezt adja, láthatod, ez a képlet helytelen.
|
| Előzmény: [800] Gézoo, 2012-05-04 08:41:01 |
|
| [801] Gézoo | 2012-05-04 09:39:51 |
 Múltkoriban Lajos bácsi felvetette a Nm mint Joule értelmű energia és a Nm mint nyomaték mértékegységes hasonlóságából adódó félreértés lehetőségét.
A "t" tempus-time-idő jele is éppen ilyen félreértés okozó.
Éppen úgy jelölünk vele időpontot mint időszakaszt.
Alma válasza kapcsán felmerülhet, hogy a t időpontot vagy t időszakaszt jelöl a válaszomban írt függvény számlálójában.
Nyilván s=v*t értelemben használva v sebességgel t időszakasz alatt való elmozdulást jelent.
Ebben az értelemben ha képeznénk x'-értékeinek különbözetét az
x'=(x-v*t)/sin(arccos(v/c)) függvénnyel, akkor időszakaszok különbözeteit képeznénk ezzel a kérdésben felvetett egyetlen t időszakasz használata helyett.
Aki rápillant azt látja itt is "t" ott is "t" azaz ugyanaz.. Pedig elvben sem lehet ugyanaz a két "t" értelmezése.
|
|
| [800] Gézoo | 2012-05-04 08:41:01 |
 Kedves Alma! Az s úthossz transzformációja
s'=s*sin(arccos(v/c)) függvénnyel végzendő.
Az x koordináta transzformációja pedig
x'=(x-v*t)/sin(arccos(v/c)) függvénnyel végzendő.
A kettő különbsége látványos.
|
| Előzmény: [799] Alma, 2012-05-04 08:35:28 |
|
|
| [798] Gézoo | 2012-05-04 06:33:25 |
 Kicsit félreérted. t#t' azt jelenti, hogy K rendszerben nyugvó megfigyelő óráján
eltelik t idő akkor K' rendszerbeli megfigyelő óráján
t'=t*1/sin(arccos(v/c)) idő telik el.
Ezért t # (ez a jel a nem egyenlő) t'
|
| Előzmény: [796] Zilberbach, 2012-05-03 14:59:39 |
|
|
| [796] Zilberbach | 2012-05-03 14:59:39 |
 Ezt a 791-es hozzászólásodat már átnéztem, már kappisgálom - valamennyire. Az általad írt: t#t' azt jelntené hogy t és t' fizikailag egyenértékűek és "szimmetrikusak" egymásra a transzformációk szempontjából?
|
| Előzmény: [791] Gézoo, 2012-05-03 10:07:53 |
|
| [795] Alma | 2012-05-03 14:55:27 |
 Z nem invariáns.
Rosszul értelmezed a hosszkontrakciót és az idődilatációt. Egy téridőtávolság áttranszformálásának tisztességes módja 1+1 dimenziós specrelben a következő:
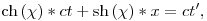
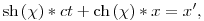
ahol 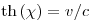 , ,  a rapiditás. a rapiditás.
|
| Előzmény: [791] Gézoo, 2012-05-03 10:07:53 |
|
| [794] Zilberbach | 2012-05-03 14:38:08 |
 Kedves Gézoo! Lehet, hogy igazad van, sajnos én ezekkel az általad leírt képletekkel nem vagyok bensőséges viszonyban, egyelőre még gondolkodnom kell az egészen. Például rá kell még jönnöm, hogy mi ez a "Z", stb. Ha valami értelmes gondolatra jutok, illetve ha kérdésem lesz, írni fogok.
|
| Előzmény: [792] Gézoo, 2012-05-03 10:11:55 |
|
| [793] Gézoo | 2012-05-03 11:25:15 |
 Vagy, hogy még érthetőbb legyen a relativitás elméletének kikezdhetetlen matematikájában lévő alapvető hiba:
Z= s*t = s'*t' = v*t2 = v'*t'2 = c*t2 = c'*t'2
azaz ahol t2 # *t'2 ott c # c'
Ez annál is nagyobb ciki, mert a relativitás elméletében
az összes transzformációt a:
c/c' = 1/(1-(v/c)2)1/2 függvénnyel végezzük,
amely arányban a posztulált állandó c fénysebesség és
a posztulátummal szemben álló c' fénysebesség aránya szerepel.
Vagyis a teljes specrel a saját posztulátumát megsértő c' sebességgel képzett hányadosra építette minden transzformációját.
|
| Előzmény: [791] Gézoo, 2012-05-03 10:07:53 |
|
|
| [791] Gézoo | 2012-05-03 10:07:53 |
 Szóval mi is ez az invariáns Z?
Legyen két rendszer közötti relatív sebesség v akkor
Ha az s az út hossza és az s út megtételéhez szükséges t idő szorzata Z=s*t akkor a v sebességű IR-ben:
t'=t/(1-(v/c)2)1/2 és s'=s*(1-(v/c)2)1/2
azaz
Z=t/(1-(v/c)2)1/2*s*(1-(v/c)2)1/2
és miután: (1-(v/c)2)1/2/(1-(v/c)2)1/2=1
Z= s*t = s'*t' = v*t2 = v'*t'2
Ez olyan egyszerű evidencia, hogy nyilván belátható.
Na de mit jelent?
K rendszerben v sebességgel t ideig haladó test a K' rendszerben v' sebességgel halad t' ideig.
Ha feltételezzük, hogy K rendszerhez rendelt koordináta rendszerben K' rendszerhez rendelt koordináta rendszer origója v sebességgel mozog t ideig, akkor ugyanezen t idejű mozgás a K' rendszerben t' ideig tart és v' sebességű a fenti evidencia értelmében.
Vagyis ha elfogadjuk azt, hogy t#t' a specrel szerint, akkor a specrelben felhasznált azonosság
amely szerint ha K rendszerben a K' koordináta rendszerének origója v sebességgel mozog t ideig, akkor K' rendszerben is v sebességgel mozog t' ideig a K rendszerhez rendelt koordináta rendszer origója.
Viszont ezen esetben a fent levezetett specreles evidencia nem teljesülhetne.
Vagyis Z # v*t'2 azaz a specrel sebesség fogalmával van egy alapvető számtani és egyben elvi hiba is.
|
| Előzmény: [786] Zilberbach, 2012-04-29 21:40:32 |
|
|
| [789] Gézoo | 2012-05-01 06:46:40 |
 Csak egy kis fizika történelem:
A kerék felfedezésétől Newtonig 8000 év telt el. Newtontól Niels Bohr-ig már csak 300 év. Niels Bohr-tól Einstein általános relativitásáig már csak 3 év telt el. És az áltrel óta stagnál a kvantummechanika.. Na jó Feynman egy picit ragozta a kvantumfizikát, mint anno Maxwell Faraday-Gauss-Lenz-Ampére törvényeit, de sok újat nem tett hozzá. Igazi továbblépés (áttörés) olyan elv lehetne amiben összekapcsolódik a téridő a görbületének okával.
Ha felismerjük, hogy van olyan részecske ami a téridő görbületét okozza akkor ez az összekapcsolódás megtörténik.
Az más kérdés, hogy azt is fel kellene ismerni, hogy a mezőket azaz az erőtereket szintén részecskék árama okozza.
Ezért sem lehet a Higgs mező éter szerűen mindent kitöltő, azaz a modern éter.
|
|
| [788] Gézoo | 2012-04-29 23:23:20 |
 Ezt az impulzus frekvencia modulációt (FM), majd a módosított impulzus frekvencia modulációt (MFM) még a mágneses adattárolásban is alkalmaztuk. (Az első floppy ás HDD lemezeken ezeket a modulációs eljárásokat alkalmaztuk.) A soros (RS232 optikai és rádiós hosszabbítóiban szintén impulzus modulációs eljárást alkalmazunk. Ezekben sincs két foton front között semmiféle hullám, semmiféle jel. Egyszerűen kikapcsolt állapotúak a sugárzók. Mégis a vételi oldalon a hangolt körökben hullámzást keltenek az impulzus sorozatok és ezen hullámok szelektív erősítésével érjük el a zavarmentes átvitelt.
|
| Előzmény: [787] Gézoo, 2012-04-29 21:41:55 |
|
| [787] Gézoo | 2012-04-29 21:41:55 |
 Pedig egyszerű.. Fogj egy lézer pointert és köss rá egy 1 ns kapuidejű meghajtót.
És bármilyen f frekvenciájú hullámot ki tudsz vele váltani ha t=1/f időnként felvillantod.
Kell egy 500 kHz-es hullámzás? Oké, állítsd a villanások közötti időt t=1/5e5=0,002 msec idejűre.. Kellene egy URH frekvencia mondjuk a sláger rádió frekvenciáján t=1/83e6= 12 ns
Két impulzus között kikapcsolhatod a lézert.. Akkor is létrejön a kívánt frekvenciájú hullámzás.
Évek óta használjuk SSB üzemű "egy impulzus" vagy ahogy mondjuk "egy hullám" modulációban.
|
| Előzmény: [785] Zilberbach, 2012-04-29 21:09:18 |
|
| [786] Zilberbach | 2012-04-29 21:40:32 |
 Na már kezdem magamtól is kapisgálni ezt a kapuzott fotonsugárzást: ez a kétréses kísérlet lenne, és valószínűleg attól tükör-kapu, hogy nem egy feketére festett lapon nyílik meg a két rés, hanem egy tükrön. Na így már megjelent a lelki szemeim előtt. Néha idő kell, míg leesik nálam a tantusz.
|
| Előzmény: [785] Zilberbach, 2012-04-29 21:09:18 |
|
| [785] Zilberbach | 2012-04-29 21:09:18 |
 "A kapuzott fotonsugárzás pedig azt bizonyítja, hogy két foton között lezárt tükör-kapu alkalmazása mellett is ugyanazon hullámkép, valamint két kapu esetében interferenciakép kialakul, mint kapuzás nélkül."-írod. Na erről kellene nekem inkább egy ábra vagy animáció, mert nem jelent meg a lelki szemeim előtt, hogy mi az a kapuzott fotonsugárzás.
|
| Előzmény: [782] Gézoo, 2012-04-29 20:29:17 |
|
| [784] Gézoo | 2012-04-29 20:56:52 |
 "A lényeg itt azon van, hogy a kétréses kísérletben kialakuló sötét és fényes sávok könnyen magyarázhatóak, ha hullámként tekintünk a fényre,"
És akkor is éppen ilyen könnyen magyarázható, ha egy tál vízbe két ponton belemártod az ujjadat és két helyen keltesz hullámokat. A keltés helyeitől mért távolságok és a keltett hullámok hullámhosszainak arányával.
"Nagyjából erről szól a Niels Bohr által megfogalmazott komplementaritás elve: a mikrovilág jelenségei (többnyire) magyarázhatók, ha hajlandóak vagyunk tudomásul venni, hogy van amikor részecskéknek és van amikor hullámoknak kell tekintenünk a mikrovilág szereplőit. "
Nos, igen.
Ez akkor is igaz, ha a részecskéket fotonáramok alkotják.
|
| Előzmény: [783] Zilberbach, 2012-04-29 20:32:46 |
|
| [783] Zilberbach | 2012-04-29 20:32:46 |
 "Interferencia mindig az anyag elektronfelhőiben jön létre. Vákuumban soha senki sem tudott kimutatni interferenciálódó fotonokat."-írod. Most esett le a tantusz hogy mire gondolsz. Arra, hogy az interferencia észlelése számunkra csak úgy lehetséges, ha a fény valami anyaggal hat kölcsön. De ez minden elektromágneses jelenségre igaz, mert végső soron még a retinánk is anyagból van. A lényeg itt azon van, hogy a kétréses kísérletben kialakuló sötét és fényes sávok könnyen magyarázhatóak, ha hullámként tekintünk a fényre, és nem magyarázhatók, ha kizárólag fotonrészecskék áramának tekintjük a fényt. Nagyjából erről szól a Niels Bohr által megfogalmazott komplementaritás elve: a mikrovilág jelenségei (többnyire) magyarázhatók, ha hajlandóak vagyunk tudomásul venni, hogy van amikor részecskéknek és van amikor hullámoknak kell tekintenünk a mikrovilág szereplőit.
|
| Előzmény: [779] Gézoo, 2012-04-29 16:08:56 |
|
|
| [781] Gézoo | 2012-04-29 20:15:03 |
 szimuláció Ezzel a szimulációval azt is megfigyelheted, hogy két résen át csepegő vízzel létrejön az interferencia kép. Ha két résen át sörétet vagy kavicsokat szórunk a víz felszínére akkor is létrejön az interferencia kép. Amely tény azt igazolja, hogy az interferencia keltéséhet a fotonoknak nem kell hullámtulajdonságokkal rendelkeznie.
A kapuzott fotonsugárzás pedig azt bizonyítja, hogy két foton között lezárt tükör-kapu alkalmazása mellett is ugyanazon hullámkép, valamint két kapu esetében interferenciakép kialakul, mint kapuzás nélkül.
Azaz két foton között nincs semmilyen olyan része-eleme a foton sugárzásnak ami hullám jellegére utalhatna.
Egyébként pedig hallottad már azt a kifejezést, hogy "zöldhullám" ? Zöld lámpától, zöld lámpáig haladó autók "hullámait" nevezzük így. Azaz semmi köze a hullámokhoz a "hullámterjedés" értelemben! A fotonok, mint autók csoportjai haladnak, autóhullámok szerű csoportokat alkotva. Vagy mint a fenti szimuláción, cseppek szerű csoportokat alkotva.
A hullámzó közeg a fotonok esetében az ernyő elektronjainak felhője. Interferencia csepegő csapokkal
"Az elektronok is gyorsulással érik el a foton-kibocsájtást. Az atomból (pl. előzetes foton általi gerjesztés után) az alacsonyabb energiájú pályára vissza-ugró elektron is gyorsul. " Pontosítsunk: egy foton kisugárzásához legalább két gyorsulás tartozik. 1. a beérkező energia (foton) okozta gyorsulás 2. a kisugárzással járó "visszaható irányú" gyorsulás A hasonlatod pedig egészen jó.
""Arra felfigyeltél, hogy a valószínűségi függvények felírhatóságának is van valószínűségi függvénye?" Az már nem igazi függvény, az már csak egy adott valószínűség "
Kicsit úgy tűnik, hogy félreértettél. A te példáddal:
Tehát van a 6-os dobásnak egy valószínűségi függvénye.
Ezt a függvényt bizonyos ismeretek felhasználásával írtuk fel.
A kérdés, mekkora annak a valószínűsége, hogy a 6-os dobás valószínűségi függvényének felírásához minden paraméterrel rendelkezünk? Azaz az egyik ( a 6-os dobás) valószínűségi függvényének felírásához szükséges paraméterek meglétének valószínűségi függvénye érdekel.
"Van egy nagyon érdekes, vagy inkább fontos és jellemző hatása a foton felhőknek, ami az anyagnak nincsen. Tudod melyik az a tulajdonság?" -írod. Így hirtelen most nem tudom mire gondolsz. "
Lassítja az időt..
|
| Előzmény: [780] Zilberbach, 2012-04-29 18:41:17 |
|
| [780] Zilberbach | 2012-04-29 18:41:17 |
 "Amikor két foton között tükörrel lezárjuk a fényutat, akkor is ugyanolyan hullámot kelt a fotonsorozat. Ergo a fotonok között nincs semmi, se hullám, se semmi más."-írod. Lehet hogy buta vagyok, de nem értem, hogy itt mire gondolsz, ezt precízebben / érthetőbben kellene megfogalmazni.
"Vákuumban soha senki sem tudott kimutatni interferenciálódó fotonokat." -írod. Én a kétréses kísérletnél, az ernyőn kialakult interferencia-csíkokra gondoltam, amikor azt írtam, hogy azt nem lehet részecske alapon magyarázni. Ez vákuumban is ugyanúgy létrejön.
"A magnós példában a membrán gyorsulással éri el a relatív hangsebességű hatást." -írod. Az elektronok is gyorsulással érik el a foton-kibocsájtást. Az atomból (pl. előzetes foton általi gerjesztés után) az alacsonyabb energiájú pályára vissza-ugró elektron is gyorsul.
"Arra felfigyeltél, hogy a valószínűségi függvények felírhatóságának is van valószínűségi függvénye?" Az már nem igazi függvény, az már csak egy adott valószínűség (aminek a valószínűsége mindíg egyenlő önmagával illetve 100 százalékkal: pl. ha a kockával 6-ost dobás valószínűsége 1/6, akkor annak a valószínűsége hogy a kockával 6-ost dobás valószínűsége = 1/6 az 100 százalék.
"Van egy nagyon érdekes, vagy inkább fontos és jellemző hatása a foton felhőknek, ami az anyagnak nincsen. Tudod melyik az a tulajdonság?" -írod. Így hirtelen most nem tudom mire gondolsz.
|
| Előzmény: [779] Gézoo, 2012-04-29 16:08:56 |
|
| [779] Gézoo | 2012-04-29 16:08:56 |
 "ha elfogadjuk a vákuumot mint az elektromágneses hullámok hordozóját "
Amikor két foton között tükörrel lezárjuk a fényutat, akkor is ugyanolyan hullámot kelt a fotonsorozat. Ergo a fotonok között nincs semmi, se hullám, se semmi más.
A magnós példában a membrán gyorsulással éri el a relatív hangsebességű hatást. Ezért csak az az egyetlen lehetőség van amivel kezdted: A fotonok az anyagban fénysebességgel tartózkodnak.
"pl. az interferenciákat nem tudnád részecske-alapon magyarázni,"
Interferencia mindig az anyag elektronfelhőiben jön létre.
Vákuumban soha senki sem tudott kimutatni interferenciálódó fotonokat.
Ez a kísérleti tény igazolja azt, hogy semmilyen fényhullám vezető éter sincs.
Ugyanis ha lenne, akkor csak interferencia létezhetne, tiszta frekvencia soha-sehova sem érkezhetne meg.
"illetve a fekete test hőmérsékleti sugárzását sem lehet hullám leírás alapján számítani, stb."
Így van.
Arra felfigyeltél, hogy a valószínűségi függvények felírhatóságának is van valószínűségi függvénye?
És arra is felfigyeltél, hogy maga Heisenberg sem tudta felírni a felírhatóság helyességének valószínűségét leíró valószínűségi függvényt?
Csak azért kérdem mert nem említetted a válaszodban..
Van egy nagyon érdekes, vagy inkább fontos és jellemző hatása a foton felhőknek, ami az anyagnak nincsen. Tudod melyik az a tulajdonság?
|
| Előzmény: [778] Zilberbach, 2012-04-29 12:17:27 |
|
| [778] Zilberbach | 2012-04-29 12:17:27 |
 "A foton fénysebességgel kerül az anyagba és fénysebességgel lép ki az anyagból. A szabály, hogy az a valami amit fénysebességen fotonnak nevezünk felgyorsulással nem veheti fel a fénysebességet.
Akkor milyen sebességen kell az anyagban tárolódnia a fotonnak ahhoz, hogy gyorsulása nélkül fénysebességen haladva léphessen ki?" -kérdezed.
A föntiekből kindulva az következnék, hogy fénysebességgel.
De így is lehet gondolkodni: legyen egy magnetofon ami fölveszi a hangot, majd egy idő múlva visszasugározza (visszajátsza). Természetesen a hang hangsebességgel lép be a magnetofonba, és hangsebességgel lép ki onnan, de nem hang sebességgel tárolódik, hanem egy egészen más formában. Lehet hogy egy kicsit erőltetett ez a magnetofon hasonlat, de arra akarok kilukadni, hogy ha elfogadjuk a vákuumot mint az elektromágneses hullámok hordozóját - amiben szigorúan csak fénysebességgel keltődhetnek az elektromágneses hullámok - akkor nincs szükségünk a föltett kérdésedre, és a válaszra sem. Korábban írtad, hogy mind a részecske, mind a hullám leírás teljes. Valójában egyik sem teljes: pl. az interferenciákat nem tudnád részecske-alapon magyarázni, illetve a fekete test hőmérsékleti sugárzását sem lehet hullám leírás alapján számítani, stb.
|
| Előzmény: [777] Gézoo, 2012-04-29 10:15:11 |
|



 a rapiditás.
a rapiditás.