|
| [814] Alma | 2012-05-08 10:26:13 |
 Igen, de itt gyorsan megjegyzem, hogy az s' mennyiség semmiképp nem interpretálható a koordináta-rendszeremben megtett útként, vagy elmozdulásként.
|
| Előzmény: [813] Gézoo, 2012-05-08 07:26:38 |
|
| [813] Gézoo | 2012-05-08 07:26:38 |
 Valóban! Elcseréltem. Ügyes vagy, hogy észrevetted!
A Te rendszeredben mért (számított) mérési adatok a vesszős, a járda rendszere a vessző nélküli. Azaz helyesen így kellett volna jelölnöm: t=t'/sin(arccos(v/c)) időszakasz hosszot.
Hiszen így jelöltük a te rendszeredben mérhető járda hosszot is: s'=s*sin(arccos(v/c)) a járda rendszerében mérhető s hosszból.
Tehát van két adatod, amit mértél, számítottál: s' és t'
és van a járda rendszerében két adat s és t.
Eddig egyetértünk?
|
| Előzmény: [812] Alma, 2012-05-07 21:20:39 |
|
|
| [811] Gézoo | 2012-05-07 21:02:44 |
 Nagyszerű!
Na most fogom a stopperemet és végigsétálok v sebességgel ezen az s úton, a kapott t időt mutató stopperemet megállítom.
Te azt figyelhetted meg, mert éppen ott voltál a járda elején az induláskor t=0 időpontban, hogy állok a Te rendszeredben és közben megy a stopperem mutatója, mozog alattam a járda. Ebből arra gondolsz, hogy én nyugvó vagyok a Te rendszeredben? Ha így van, akkor jól gondolod. Arra gondolsz, hogy a stopperem a Te rendszeredben nyugodva a Te rendszeredben érvényes időt mutatta? Ha így van, akkor ezt is jól gondolod.
Na most a járdán nyugvó óra vajon mit mutatott amikor a járda végére léptem és ettől megállt?
Jól tippelek ha azt mondom, hogy szerinted a járdán nyugvó óra
ami akkor indult el amikor a járdára léptem és akkor állt meg amikor a járda végére érkeztem az
t'=t/sin(arccos(v/c)) időszakasz hosszot mutat?
|
| Előzmény: [810] Alma, 2012-05-07 19:42:51 |
|
|
| [809] Gézoo | 2012-05-07 19:27:23 |
 Kedves Alma!
Figyelj csak! Másról beszélünk.
Legyen egy s hosszú járda nyugalomban az én rendszeremben, te mozogsz a járdámhoz képest v sebességgel. Ezért a teljes járda mozog a te rendszeredben.
Na akkor a te rendszeredben milyen hosszú az én rendszeremben nyugvó járda? Nyilván elsőre tudtad, hogy te az én járdámat s'=s*sin(arccos(v/c)) hosszúnak méred. Ebben egyetértünk?
|
| Előzmény: [808] Alma, 2012-05-07 18:11:14 |
|
| [808] Alma | 2012-05-07 18:11:14 |
 Könyörgöm ne nézz már annyira hülyének, hogy általános iskolás átalakításokat magyarázol el nekem.
s'=s*sin(arccos(v/c))
Ez a rossz képlet, és megint ezt használod. Ez a képlet triviálisan hülyeség. A mozgásnak van kezdete, van vége, és nem ugyanabban az időpillanatban van ez a kettő. NEM HASZNÁLHATOD A LORENTZ-KONTRAKCIÓS KÉPLETET. Az nem erre való. Az egyidejű téridőtávolság transzformálására való. Középiskolában még csak ez fér bele a tananyagba. Nem lehet felépíteni a specrelt, mert nincs rá elég idő. Attól még megvan a tisztességes elmélete, és ha ezt nem ismered, még nem lesz ellentmondásos és rossz az egész.
Az előbb egyeztél bele abba, hogy ha áttérsz a mozgással azonos sebességű rendszerbe, a megtett út 0 lesz.
s'=0
Szerinted az s'=s*sin(arccos(v/c)) képlet ezt adja? Hát nem. Nem ez a jó képlet. Szerintem kezd el olvasni a Taylor-Wheeler Téridőfizika című könyvet, abból meg lehet érteni a specrel alapjait. Függvénytáblázatból nem.
|
| Előzmény: [807] Gézoo, 2012-05-07 17:12:37 |
|
| [807] Gézoo | 2012-05-07 17:12:37 |
 Kedves Alma! Sok oka van. Egyik, hogy Z valóban invariáns.
Nézd csak! Z=s*t=s'*t' ezt "állítottam".
s'=s*sin(arccos(v/c)) t'=t/sin(arccos(v/c))
ismeretében helyettesítsünk be Z függvényébe s' és t' helyére:
Z=s*t= s*sin(arccos(v/c))*t/sin(arccos(v/c))
Nem állna fent az egyenlőség?
Nekem úgy tűnik, hogy a Lorentz transzformáció szimmetriája szerint sin(arccos(v/c))/sin(arccos(v/c)) = 1
Azaz a behelyettesített oldalon elvégezve az egyszerűsítést:
Z=s*t= s*t marad..
és miután s*t=s*t ez nyilvánvaló, ezért
Z=s*t=s'*t' függvény helyessége is nyilvánvaló.
Miért írok ilyeneket?
Nos, mert a specrel egy jól megfontolt PR fogással élve úgy lett beharangozva, köztudatba beültetve, hogy
- valós fizikai változást ír le, pedig csupán egy a mozgási sebességek viszonyából fakadó mérési hiba kompenzálására szolgál.
- hú de bonyolult valami, a megértésére egyrészt nincs szükség, másrészt olyan nagyon érthetetlen, hogy ne is próbálja halandó ember megérteni.
Ezek egyike sem igaz. Másrészt a mai hétköznapi gyakorlatban számos olyan eszközt használunk és a mérnöki gyakorlatban pedig tervezünk ami már eddig is használta a specrelt, és egyre több olyan van ami már az áltrelt is alkalmazza.
Ennek ellenére nem csak "mezei" mérnökök, de még a végzett fizikusok is szinte csak hallomásból ismerik az áltrelt.
Azt elismerem, hogy az áltrel egyes részei kicsit elbonyolítottak. Viszont a lényege egyetlen mondattal leírható: Minden folyamatba, jelenségben a méretek képződésétől az energiák hasznosításáig a Idő múlási sebessége az egyetlen alapvetően meghatározó tényező.
Azaz minden amit látunk, érintünk attól éppen olyan, hogy az idő múlási sebessége hogyan változik a környezetében.
Erre pedig, mint minden vita, a mi vitánk is felhívja a figyelmet.
Még az is megeshet, hogy egyesek éppen azért fognak belemélyedni a megismerésébe, mert nem hiszik el azt amit itt olvastak erről a témáról.
|
| Előzmény: [806] Alma, 2012-05-07 14:01:23 |
|
| [806] Alma | 2012-05-07 14:01:23 |
 Kedves Gézoo!
Nem értem akkor, miért állítasz olyat, hogy s*t=s'*t', amikor ez láthatóan nem igaz.
Nem értem, miért akarod ebből a relativitáselmélet hibáját kihozni, amikor csak rosszul interpretálod a relativitáselmélet állításait. Relativitáselméletben nincs külön az út megváltozása, és külön az időtartam megváltozása, hanem ezek összefüggnek. Nem tudod simán ugyanannál az esetnél a távolságot kontraktálni és az időt dilatálni. Nincs külön tér és idő, téridő van.
|
| Előzmény: [805] Gézoo, 2012-05-07 11:24:34 |
|
|
| [804] Alma | 2012-05-07 10:57:51 |
 Kedves Gézoo!
Egyszerűbben:
Ha van egy egyenes vonaló egyenletes mozgásod, és áttérsz egy olyan koordinátarendszerbe, melynek sebessége megegyezik a mozgás sebességével, abban a koordinátarendszerben a test áll, mozgást nem végez, az általa megtett út 0.
|
| Előzmény: [803] Gézoo, 2012-05-07 00:57:03 |
|
| [803] Gézoo | 2012-05-07 00:57:03 |
 Kedves Alma!
A vonaton ülő ember úthossza helyett a vonat hossza lenne a válasz a kérdésemre. Azaz nem kell két mozgást számolni egyetlen mozgás helyett.
Az eredeti felvetésben az szerepelt, hogy van egy s hossz.
Itt nincs idő, csak s hossz. Ez a hossz pedig s'=s*sin(arccos(v/c)) függvénnyel transzformálható.
Az egy másik kérdés volt, hogy ha v sebességgel azaz t=s/v idő alatt végigsétál valaki az s hosszú úton, akkor az út végpontján x=0 elmozdulással transzformált óra állás pedig t'=t/sin(arccos(v/c)) függvénnyel transzformálandó.
Ugyanezt a két függvényt akkor is megkaphatjuk, ha t=0=t' időpontból elindul egy v sebességű mozgás és a relatív időpontokban a K rendszerben t=s/v és K' rendszerben t'=s'/v időpontban a végére megérkezik. Az eredmény így is ugyanaz, mint amit a fenti két függvénnyel kapunk.
Ennek az oka egyszerű K rendszerben a K' rendszerhez tartozó hosszkontrakciót és idő dilatációt mérhetjük. K' rendszerben pedig a K rendszer méretei szenvednek kontrakciót és az óra állásai dilatációt.
Ezért igazából a Z=s*t=s'*t' invariáns egy evidencia, mert a transzformációk szimmetrikusak, ezért a szorzatuk mindig 1 azaz egy értékű szorzótényezőt alkot.
|
| Előzmény: [802] Alma, 2012-05-07 00:07:31 |
|
| [802] Alma | 2012-05-07 00:07:31 |
 Kedves Gézoo!
Nem, ebben nincs igazad, a "s'=s*sin(arccos(v/c))" képlet nem adja meg az úthossz transzformáltját.
Épp a minap tartottam egy előadást egy ismeretterjesztő egyetemi konferencián, mely témája súrolta a speciális relativitáselméletet, és ott is igyekeztem illusztrálni két téridőesemény térbeli távolságának változását ha áttérünk más koordináta-rendszerre. Következőképp érveltem:
Vegyünk két téridőeseményt: ülünk egy vonaton, a vonat indulása 14:00 Budapest, érkezés 17:00 Pécs. A Földhöz rögzített koordináta-rendszerben az indulás és a megérkezés térbeli távolsága, mint tudjuk, körülbelül 200 km. Nézzük meg ugyanezt a vonathoz rögzített koordináta-rendszerben! Mit látunk onnan? Az utas ül a székén, nem mozdul egész út során, és valahogy mégis eljut Budapestről Pécsre. Abban a koordináta-rendszerben 0 a sebessége, mozgást nem végez. Nincs megtett út. Ebből pedig ugye következik, hogy a vonathoz rögzített koordináta-rendszerben az indulás és érkezés téridőesemények térbeli távolsága 0.
A "s'=s*sin(arccos(v/c))" képlet természetesen nem ezt adja, láthatod, ez a képlet helytelen.
|
| Előzmény: [800] Gézoo, 2012-05-04 08:41:01 |
|
| [801] Gézoo | 2012-05-04 09:39:51 |
 Múltkoriban Lajos bácsi felvetette a Nm mint Joule értelmű energia és a Nm mint nyomaték mértékegységes hasonlóságából adódó félreértés lehetőségét.
A "t" tempus-time-idő jele is éppen ilyen félreértés okozó.
Éppen úgy jelölünk vele időpontot mint időszakaszt.
Alma válasza kapcsán felmerülhet, hogy a t időpontot vagy t időszakaszt jelöl a válaszomban írt függvény számlálójában.
Nyilván s=v*t értelemben használva v sebességgel t időszakasz alatt való elmozdulást jelent.
Ebben az értelemben ha képeznénk x'-értékeinek különbözetét az
x'=(x-v*t)/sin(arccos(v/c)) függvénnyel, akkor időszakaszok különbözeteit képeznénk ezzel a kérdésben felvetett egyetlen t időszakasz használata helyett.
Aki rápillant azt látja itt is "t" ott is "t" azaz ugyanaz.. Pedig elvben sem lehet ugyanaz a két "t" értelmezése.
|
|
| [800] Gézoo | 2012-05-04 08:41:01 |
 Kedves Alma! Az s úthossz transzformációja
s'=s*sin(arccos(v/c)) függvénnyel végzendő.
Az x koordináta transzformációja pedig
x'=(x-v*t)/sin(arccos(v/c)) függvénnyel végzendő.
A kettő különbsége látványos.
|
| Előzmény: [799] Alma, 2012-05-04 08:35:28 |
|
|
| [798] Gézoo | 2012-05-04 06:33:25 |
 Kicsit félreérted. t#t' azt jelenti, hogy K rendszerben nyugvó megfigyelő óráján
eltelik t idő akkor K' rendszerbeli megfigyelő óráján
t'=t*1/sin(arccos(v/c)) idő telik el.
Ezért t # (ez a jel a nem egyenlő) t'
|
| Előzmény: [796] Zilberbach, 2012-05-03 14:59:39 |
|
|
| [796] Zilberbach | 2012-05-03 14:59:39 |
 Ezt a 791-es hozzászólásodat már átnéztem, már kappisgálom - valamennyire. Az általad írt: t#t' azt jelntené hogy t és t' fizikailag egyenértékűek és "szimmetrikusak" egymásra a transzformációk szempontjából?
|
| Előzmény: [791] Gézoo, 2012-05-03 10:07:53 |
|
| [795] Alma | 2012-05-03 14:55:27 |
 Z nem invariáns.
Rosszul értelmezed a hosszkontrakciót és az idődilatációt. Egy téridőtávolság áttranszformálásának tisztességes módja 1+1 dimenziós specrelben a következő:
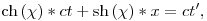
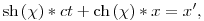
ahol 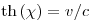 , ,  a rapiditás. a rapiditás.
|
| Előzmény: [791] Gézoo, 2012-05-03 10:07:53 |
|
| [794] Zilberbach | 2012-05-03 14:38:08 |
 Kedves Gézoo! Lehet, hogy igazad van, sajnos én ezekkel az általad leírt képletekkel nem vagyok bensőséges viszonyban, egyelőre még gondolkodnom kell az egészen. Például rá kell még jönnöm, hogy mi ez a "Z", stb. Ha valami értelmes gondolatra jutok, illetve ha kérdésem lesz, írni fogok.
|
| Előzmény: [792] Gézoo, 2012-05-03 10:11:55 |
|
| [793] Gézoo | 2012-05-03 11:25:15 |
 Vagy, hogy még érthetőbb legyen a relativitás elméletének kikezdhetetlen matematikájában lévő alapvető hiba:
Z= s*t = s'*t' = v*t2 = v'*t'2 = c*t2 = c'*t'2
azaz ahol t2 # *t'2 ott c # c'
Ez annál is nagyobb ciki, mert a relativitás elméletében
az összes transzformációt a:
c/c' = 1/(1-(v/c)2)1/2 függvénnyel végezzük,
amely arányban a posztulált állandó c fénysebesség és
a posztulátummal szemben álló c' fénysebesség aránya szerepel.
Vagyis a teljes specrel a saját posztulátumát megsértő c' sebességgel képzett hányadosra építette minden transzformációját.
|
| Előzmény: [791] Gézoo, 2012-05-03 10:07:53 |
|
|
| [791] Gézoo | 2012-05-03 10:07:53 |
 Szóval mi is ez az invariáns Z?
Legyen két rendszer közötti relatív sebesség v akkor
Ha az s az út hossza és az s út megtételéhez szükséges t idő szorzata Z=s*t akkor a v sebességű IR-ben:
t'=t/(1-(v/c)2)1/2 és s'=s*(1-(v/c)2)1/2
azaz
Z=t/(1-(v/c)2)1/2*s*(1-(v/c)2)1/2
és miután: (1-(v/c)2)1/2/(1-(v/c)2)1/2=1
Z= s*t = s'*t' = v*t2 = v'*t'2
Ez olyan egyszerű evidencia, hogy nyilván belátható.
Na de mit jelent?
K rendszerben v sebességgel t ideig haladó test a K' rendszerben v' sebességgel halad t' ideig.
Ha feltételezzük, hogy K rendszerhez rendelt koordináta rendszerben K' rendszerhez rendelt koordináta rendszer origója v sebességgel mozog t ideig, akkor ugyanezen t idejű mozgás a K' rendszerben t' ideig tart és v' sebességű a fenti evidencia értelmében.
Vagyis ha elfogadjuk azt, hogy t#t' a specrel szerint, akkor a specrelben felhasznált azonosság
amely szerint ha K rendszerben a K' koordináta rendszerének origója v sebességgel mozog t ideig, akkor K' rendszerben is v sebességgel mozog t' ideig a K rendszerhez rendelt koordináta rendszer origója.
Viszont ezen esetben a fent levezetett specreles evidencia nem teljesülhetne.
Vagyis Z # v*t'2 azaz a specrel sebesség fogalmával van egy alapvető számtani és egyben elvi hiba is.
|
| Előzmény: [786] Zilberbach, 2012-04-29 21:40:32 |
|



 a rapiditás.
a rapiditás.