| [827] Gézoo | 2012-05-09 10:24:24 |
 Jól mondod.. Ez a lényeg.
Az invariencia fennmarad akár s'/t' akár s'*t' a végzett művelet.
Sőt!
s'=s*sin(arccos(v/c)) és t'=t/sin(arccos(v/c) függvények tovább erősítik ezt a megállapítást.
Hogy még szemléletesebb legyen éljünk b=sin(arccos(v/c) alakkal: s'=s*b és t'=t/b
azaz a kérdés, hogy s*t egyenlő-e s'*t' szorzattal?
végezzük el a műveletet s'=s*b és t'=t/b egyenlőségeket felhasználva s*t ?=? s*b*t/b
átrendezve:
s*t ?=? s*t* b/b ahol b/b=1 ott
s*t=s*t eredményt kapunk, tehát ha
s/t=s'/t' invariáns akkor s*t=s'*t' szintén invariáns
|
| Előzmény: [826] nadorp, 2012-05-09 08:59:25 |
|
| [826] nadorp | 2012-05-09 08:59:25 |
 Bocs, hogy beleszólok. Előre bocsátom, hogy a relativitáselmélethez nem értek, és ha hülyeséget írnék, már most meggyónom :-). Az nem világos, hogy itt a matematika szabályai "felborulnak"? Gondolok arra, hogy 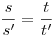 és az állítás szerint a jobb oldal invariáns a reciprok képzésre. De ez nem igaz, mert reciprokot véve a jobb oldal és az állítás szerint a jobb oldal invariáns a reciprok képzésre. De ez nem igaz, mert reciprokot véve a jobb oldal  lesz. Más analógiát véve, ha veszünk egy háromszöget, aminek két oldala a,b, akkor a hozzá hasonló háromszögek közt az lesz. Más analógiát véve, ha veszünk egy háromszöget, aminek két oldala a,b, akkor a hozzá hasonló háromszögek közt az 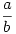 mennyiség invariáns lesz, de ab nem lesz az. Vagy a fentiek nem húzhatók rá a szóban forgó példára? mennyiség invariáns lesz, de ab nem lesz az. Vagy a fentiek nem húzhatók rá a szóban forgó példára?
|
| Előzmény: [825] Gézoo, 2012-05-09 07:08:34 |
|
| [825] Gézoo | 2012-05-09 07:08:34 |
 Nagyszerű!
Tehát, ha s*z = s'*z' invariáns, akkor t=1/z alakkal behelyettesítve is invariáns, mivel csak a reciprokáról van szó s*(1/z)= s'*(1/z')
Vagy szerinted van oka annak, hogy a reciprokkal elveszítjük az invarienciát mint tulajdonságot?
|
| Előzmény: [824] Alma, 2012-05-08 21:47:23 |
|
|
| [823] Gézoo | 2012-05-08 21:05:16 |
 Nos, jó. Egyszerűsítsünk!
s/t=s'/t' ebben egyetértettünk, akkor ezzel ebben is:
s * (1/t) =s'* (1/t')
vagy akár z=1/t behelyettesítéssel ebben is:
s*z = s'*z'
Jól gondolom?
|
| Előzmény: [822] Alma, 2012-05-08 15:58:25 |
|
| [822] Alma | 2012-05-08 15:58:25 |
 t2*s/t=t'2*s'/t' miért lenne igaz, ha s/t=s'/t'? t t'. t'.
|
|
|
|
|
|
| [817] Gézoo | 2012-05-08 11:40:30 |
 Tehát ha jól értelek, akkor szerinted is érvényes:
v = s/t = s'/t' ?
:D Na akkor szorozzuk meg egy t2 -el minden tagot!
Az egyenlőség nem változhat,
v * t2 = t2*s/t = t'2*s'/t'
Eddig érthető?
|
| Előzmény: [816] Alma, 2012-05-08 11:26:56 |
|
| [816] Alma | 2012-05-08 11:26:56 |
 Pontosan, így gondolom. Az én koordináta-rendszeremben, mint megállapodtunk, a tiedben mozgó test áll, 0 a sebessége.
Az én rendszeremben mozog a járdád, így kerül arrébb a test a járdához képest. Nem a testnek van sebessége, hanem a járdának. Ha kettőnk közötti koordináta-rendszert vennénk, akkor még bonyolultabb lenne a helyzet, hiszen akkor a járda és a test is mozogna, valamint a járda nyugalmi hossza is kontraktálódna természetesen.
|
| Előzmény: [815] Gézoo, 2012-05-08 11:20:58 |
|
|
| [814] Alma | 2012-05-08 10:26:13 |
 Igen, de itt gyorsan megjegyzem, hogy az s' mennyiség semmiképp nem interpretálható a koordináta-rendszeremben megtett útként, vagy elmozdulásként.
|
| Előzmény: [813] Gézoo, 2012-05-08 07:26:38 |
|
| [813] Gézoo | 2012-05-08 07:26:38 |
 Valóban! Elcseréltem. Ügyes vagy, hogy észrevetted!
A Te rendszeredben mért (számított) mérési adatok a vesszős, a járda rendszere a vessző nélküli. Azaz helyesen így kellett volna jelölnöm: t=t'/sin(arccos(v/c)) időszakasz hosszot.
Hiszen így jelöltük a te rendszeredben mérhető járda hosszot is: s'=s*sin(arccos(v/c)) a járda rendszerében mérhető s hosszból.
Tehát van két adatod, amit mértél, számítottál: s' és t'
és van a járda rendszerében két adat s és t.
Eddig egyetértünk?
|
| Előzmény: [812] Alma, 2012-05-07 21:20:39 |
|
|
| [811] Gézoo | 2012-05-07 21:02:44 |
 Nagyszerű!
Na most fogom a stopperemet és végigsétálok v sebességgel ezen az s úton, a kapott t időt mutató stopperemet megállítom.
Te azt figyelhetted meg, mert éppen ott voltál a járda elején az induláskor t=0 időpontban, hogy állok a Te rendszeredben és közben megy a stopperem mutatója, mozog alattam a járda. Ebből arra gondolsz, hogy én nyugvó vagyok a Te rendszeredben? Ha így van, akkor jól gondolod. Arra gondolsz, hogy a stopperem a Te rendszeredben nyugodva a Te rendszeredben érvényes időt mutatta? Ha így van, akkor ezt is jól gondolod.
Na most a járdán nyugvó óra vajon mit mutatott amikor a járda végére léptem és ettől megállt?
Jól tippelek ha azt mondom, hogy szerinted a járdán nyugvó óra
ami akkor indult el amikor a járdára léptem és akkor állt meg amikor a járda végére érkeztem az
t'=t/sin(arccos(v/c)) időszakasz hosszot mutat?
|
| Előzmény: [810] Alma, 2012-05-07 19:42:51 |
|
|
| [809] Gézoo | 2012-05-07 19:27:23 |
 Kedves Alma!
Figyelj csak! Másról beszélünk.
Legyen egy s hosszú járda nyugalomban az én rendszeremben, te mozogsz a járdámhoz képest v sebességgel. Ezért a teljes járda mozog a te rendszeredben.
Na akkor a te rendszeredben milyen hosszú az én rendszeremben nyugvó járda? Nyilván elsőre tudtad, hogy te az én járdámat s'=s*sin(arccos(v/c)) hosszúnak méred. Ebben egyetértünk?
|
| Előzmény: [808] Alma, 2012-05-07 18:11:14 |
|
| [808] Alma | 2012-05-07 18:11:14 |
 Könyörgöm ne nézz már annyira hülyének, hogy általános iskolás átalakításokat magyarázol el nekem.
s'=s*sin(arccos(v/c))
Ez a rossz képlet, és megint ezt használod. Ez a képlet triviálisan hülyeség. A mozgásnak van kezdete, van vége, és nem ugyanabban az időpillanatban van ez a kettő. NEM HASZNÁLHATOD A LORENTZ-KONTRAKCIÓS KÉPLETET. Az nem erre való. Az egyidejű téridőtávolság transzformálására való. Középiskolában még csak ez fér bele a tananyagba. Nem lehet felépíteni a specrelt, mert nincs rá elég idő. Attól még megvan a tisztességes elmélete, és ha ezt nem ismered, még nem lesz ellentmondásos és rossz az egész.
Az előbb egyeztél bele abba, hogy ha áttérsz a mozgással azonos sebességű rendszerbe, a megtett út 0 lesz.
s'=0
Szerinted az s'=s*sin(arccos(v/c)) képlet ezt adja? Hát nem. Nem ez a jó képlet. Szerintem kezd el olvasni a Taylor-Wheeler Téridőfizika című könyvet, abból meg lehet érteni a specrel alapjait. Függvénytáblázatból nem.
|
| Előzmény: [807] Gézoo, 2012-05-07 17:12:37 |
|
| [807] Gézoo | 2012-05-07 17:12:37 |
 Kedves Alma! Sok oka van. Egyik, hogy Z valóban invariáns.
Nézd csak! Z=s*t=s'*t' ezt "állítottam".
s'=s*sin(arccos(v/c)) t'=t/sin(arccos(v/c))
ismeretében helyettesítsünk be Z függvényébe s' és t' helyére:
Z=s*t= s*sin(arccos(v/c))*t/sin(arccos(v/c))
Nem állna fent az egyenlőség?
Nekem úgy tűnik, hogy a Lorentz transzformáció szimmetriája szerint sin(arccos(v/c))/sin(arccos(v/c)) = 1
Azaz a behelyettesített oldalon elvégezve az egyszerűsítést:
Z=s*t= s*t marad..
és miután s*t=s*t ez nyilvánvaló, ezért
Z=s*t=s'*t' függvény helyessége is nyilvánvaló.
Miért írok ilyeneket?
Nos, mert a specrel egy jól megfontolt PR fogással élve úgy lett beharangozva, köztudatba beültetve, hogy
- valós fizikai változást ír le, pedig csupán egy a mozgási sebességek viszonyából fakadó mérési hiba kompenzálására szolgál.
- hú de bonyolult valami, a megértésére egyrészt nincs szükség, másrészt olyan nagyon érthetetlen, hogy ne is próbálja halandó ember megérteni.
Ezek egyike sem igaz. Másrészt a mai hétköznapi gyakorlatban számos olyan eszközt használunk és a mérnöki gyakorlatban pedig tervezünk ami már eddig is használta a specrelt, és egyre több olyan van ami már az áltrelt is alkalmazza.
Ennek ellenére nem csak "mezei" mérnökök, de még a végzett fizikusok is szinte csak hallomásból ismerik az áltrelt.
Azt elismerem, hogy az áltrel egyes részei kicsit elbonyolítottak. Viszont a lényege egyetlen mondattal leírható: Minden folyamatba, jelenségben a méretek képződésétől az energiák hasznosításáig a Idő múlási sebessége az egyetlen alapvetően meghatározó tényező.
Azaz minden amit látunk, érintünk attól éppen olyan, hogy az idő múlási sebessége hogyan változik a környezetében.
Erre pedig, mint minden vita, a mi vitánk is felhívja a figyelmet.
Még az is megeshet, hogy egyesek éppen azért fognak belemélyedni a megismerésébe, mert nem hiszik el azt amit itt olvastak erről a témáról.
|
| Előzmény: [806] Alma, 2012-05-07 14:01:23 |
|
| [806] Alma | 2012-05-07 14:01:23 |
 Kedves Gézoo!
Nem értem akkor, miért állítasz olyat, hogy s*t=s'*t', amikor ez láthatóan nem igaz.
Nem értem, miért akarod ebből a relativitáselmélet hibáját kihozni, amikor csak rosszul interpretálod a relativitáselmélet állításait. Relativitáselméletben nincs külön az út megváltozása, és külön az időtartam megváltozása, hanem ezek összefüggnek. Nem tudod simán ugyanannál az esetnél a távolságot kontraktálni és az időt dilatálni. Nincs külön tér és idő, téridő van.
|
| Előzmény: [805] Gézoo, 2012-05-07 11:24:34 |
|
|
| [804] Alma | 2012-05-07 10:57:51 |
 Kedves Gézoo!
Egyszerűbben:
Ha van egy egyenes vonaló egyenletes mozgásod, és áttérsz egy olyan koordinátarendszerbe, melynek sebessége megegyezik a mozgás sebességével, abban a koordinátarendszerben a test áll, mozgást nem végez, az általa megtett út 0.
|
| Előzmény: [803] Gézoo, 2012-05-07 00:57:03 |
|
| [803] Gézoo | 2012-05-07 00:57:03 |
 Kedves Alma!
A vonaton ülő ember úthossza helyett a vonat hossza lenne a válasz a kérdésemre. Azaz nem kell két mozgást számolni egyetlen mozgás helyett.
Az eredeti felvetésben az szerepelt, hogy van egy s hossz.
Itt nincs idő, csak s hossz. Ez a hossz pedig s'=s*sin(arccos(v/c)) függvénnyel transzformálható.
Az egy másik kérdés volt, hogy ha v sebességgel azaz t=s/v idő alatt végigsétál valaki az s hosszú úton, akkor az út végpontján x=0 elmozdulással transzformált óra állás pedig t'=t/sin(arccos(v/c)) függvénnyel transzformálandó.
Ugyanezt a két függvényt akkor is megkaphatjuk, ha t=0=t' időpontból elindul egy v sebességű mozgás és a relatív időpontokban a K rendszerben t=s/v és K' rendszerben t'=s'/v időpontban a végére megérkezik. Az eredmény így is ugyanaz, mint amit a fenti két függvénnyel kapunk.
Ennek az oka egyszerű K rendszerben a K' rendszerhez tartozó hosszkontrakciót és idő dilatációt mérhetjük. K' rendszerben pedig a K rendszer méretei szenvednek kontrakciót és az óra állásai dilatációt.
Ezért igazából a Z=s*t=s'*t' invariáns egy evidencia, mert a transzformációk szimmetrikusak, ezért a szorzatuk mindig 1 azaz egy értékű szorzótényezőt alkot.
|
| Előzmény: [802] Alma, 2012-05-07 00:07:31 |
|



 t'.
t'.