| [834] Alma | 2012-05-09 14:52:02 |
 Testnek neveztem azt, ami a te rendszeredben mozog. A járdának van sebessége, meg is mondtam, hogy mennyinek gondolom, s'/t', ahogy te is.
|
| Előzmény: [833] Gézoo, 2012-05-09 13:14:05 |
|
| [833] Gézoo | 2012-05-09 13:14:05 |
 Tehát a járda s' (azaz s'=s*ß rövidült "állapotban" :) ) hosszának egyik vége érkezzen be a Te rendszered egy pontjára t'=0 időpontban és méred az áthaladás idejét t'>0 értéket kapsz. Nyilván az v'=s'/t' a mozgó járda egy pontjának a Te rendszeredben mért sebességét adja..
"De attól, hogy van egy hosszúságadatom, és van egy időadatom, attól a hányadosuk nem lesz a test sebessége a rendszeremben."
Hogy érted, hogy ez a sebesség nem a járda sebessége a Te rendszeredben?
|
| Előzmény: [832] Alma, 2012-05-09 12:55:43 |
|
| [832] Alma | 2012-05-09 12:55:43 |
 Nem értek egyet. Mint már többször mondtam, az én rendszeremben nem mozog a vizsgált test, nulla a sebessége és nulla a megtett út.
A te rendszeredben nyugalomban lévő járda hossza az én rendszeremben
s'=s*sin(arccos(v/c)).
Ezzel egyetértek. Ha végigsétálsz a járdán, a mozgás idejét én, az én rendszereben megmérve ha t' értéket kapok, akkor az, a te rendszeredben
t=t'/sin(arccos(v/c)
időtartam lesz. Ezzel is egyetértek. Így definiálva a mennyiségeket még s/t=s'/t'-vel is egyetértek.
De attól, hogy van egy hosszúságadatom, és van egy időadatom, attól a hányadosuk nem lesz a test sebessége a rendszeremben. Abban a trivialitásban megegyezhetünk, hogy a te rendszeredben a test ugyanakkora sebességgel halad, mint az én rendszeremben a járda halad visszafelé.
|
| Előzmény: [831] Gézoo, 2012-05-09 12:42:23 |
|
| [831] Gézoo | 2012-05-09 12:42:23 |
 Nagyon jó! Szóval hogy is van ez? a Te rendszered a K' rendszer az s' és t' mérési adatokkal, járda rendszere a K rendszer s és t adatokkal.
A Te rendszeredben mértünk s'=s*ß hosszon áthaladás alatt, t' időt, vagyis v'=s'/t' sebességet.
A járda rendszerében v=s/t
A két v=v' egyenlő nagyságú. (Bár nem szokás v' jelölés, mert az egyenlőség léte alapfelvetés.)
Így egyetértünk?
|
| Előzmény: [828] Alma, 2012-05-09 12:21:07 |
|
|
|
| [828] Alma | 2012-05-09 12:21:07 |
 Álljon meg a menet, kezdesz ködösíteni. Világosan fogalmazz! Írd le, hogy szerinted az
s*z=s'*z'
egyenletből hogyan következik az
s/z=s'/z'
egyenlet, mert ez nem puszta matematikai átalakítás.
Megjegyezném, hogy az én, mozgó rendszerem t' idejét projektáltad át a járdához rögzített rendszerbe, vagyis helyesen az idődilatáció:
t=t'/sin(arccos(v/c),
mint ahogy ezt korábban közösen elfogadtuk. Ebből következően az utána levő levezetésed hamis.
|
| Előzmény: [827] Gézoo, 2012-05-09 10:24:24 |
|
| [827] Gézoo | 2012-05-09 10:24:24 |
 Jól mondod.. Ez a lényeg.
Az invariencia fennmarad akár s'/t' akár s'*t' a végzett művelet.
Sőt!
s'=s*sin(arccos(v/c)) és t'=t/sin(arccos(v/c) függvények tovább erősítik ezt a megállapítást.
Hogy még szemléletesebb legyen éljünk b=sin(arccos(v/c) alakkal: s'=s*b és t'=t/b
azaz a kérdés, hogy s*t egyenlő-e s'*t' szorzattal?
végezzük el a műveletet s'=s*b és t'=t/b egyenlőségeket felhasználva s*t ?=? s*b*t/b
átrendezve:
s*t ?=? s*t* b/b ahol b/b=1 ott
s*t=s*t eredményt kapunk, tehát ha
s/t=s'/t' invariáns akkor s*t=s'*t' szintén invariáns
|
| Előzmény: [826] nadorp, 2012-05-09 08:59:25 |
|
| [826] nadorp | 2012-05-09 08:59:25 |
 Bocs, hogy beleszólok. Előre bocsátom, hogy a relativitáselmélethez nem értek, és ha hülyeséget írnék, már most meggyónom :-). Az nem világos, hogy itt a matematika szabályai "felborulnak"? Gondolok arra, hogy 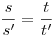 és az állítás szerint a jobb oldal invariáns a reciprok képzésre. De ez nem igaz, mert reciprokot véve a jobb oldal és az állítás szerint a jobb oldal invariáns a reciprok képzésre. De ez nem igaz, mert reciprokot véve a jobb oldal  lesz. Más analógiát véve, ha veszünk egy háromszöget, aminek két oldala a,b, akkor a hozzá hasonló háromszögek közt az lesz. Más analógiát véve, ha veszünk egy háromszöget, aminek két oldala a,b, akkor a hozzá hasonló háromszögek közt az 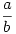 mennyiség invariáns lesz, de ab nem lesz az. Vagy a fentiek nem húzhatók rá a szóban forgó példára? mennyiség invariáns lesz, de ab nem lesz az. Vagy a fentiek nem húzhatók rá a szóban forgó példára?
|
| Előzmény: [825] Gézoo, 2012-05-09 07:08:34 |
|
| [825] Gézoo | 2012-05-09 07:08:34 |
 Nagyszerű!
Tehát, ha s*z = s'*z' invariáns, akkor t=1/z alakkal behelyettesítve is invariáns, mivel csak a reciprokáról van szó s*(1/z)= s'*(1/z')
Vagy szerinted van oka annak, hogy a reciprokkal elveszítjük az invarienciát mint tulajdonságot?
|
| Előzmény: [824] Alma, 2012-05-08 21:47:23 |
|
|
| [823] Gézoo | 2012-05-08 21:05:16 |
 Nos, jó. Egyszerűsítsünk!
s/t=s'/t' ebben egyetértettünk, akkor ezzel ebben is:
s * (1/t) =s'* (1/t')
vagy akár z=1/t behelyettesítéssel ebben is:
s*z = s'*z'
Jól gondolom?
|
| Előzmény: [822] Alma, 2012-05-08 15:58:25 |
|
| [822] Alma | 2012-05-08 15:58:25 |
 t2*s/t=t'2*s'/t' miért lenne igaz, ha s/t=s'/t'? t t'. t'.
|
|
|
|
|
|
| [817] Gézoo | 2012-05-08 11:40:30 |
 Tehát ha jól értelek, akkor szerinted is érvényes:
v = s/t = s'/t' ?
:D Na akkor szorozzuk meg egy t2 -el minden tagot!
Az egyenlőség nem változhat,
v * t2 = t2*s/t = t'2*s'/t'
Eddig érthető?
|
| Előzmény: [816] Alma, 2012-05-08 11:26:56 |
|
| [816] Alma | 2012-05-08 11:26:56 |
 Pontosan, így gondolom. Az én koordináta-rendszeremben, mint megállapodtunk, a tiedben mozgó test áll, 0 a sebessége.
Az én rendszeremben mozog a járdád, így kerül arrébb a test a járdához képest. Nem a testnek van sebessége, hanem a járdának. Ha kettőnk közötti koordináta-rendszert vennénk, akkor még bonyolultabb lenne a helyzet, hiszen akkor a járda és a test is mozogna, valamint a járda nyugalmi hossza is kontraktálódna természetesen.
|
| Előzmény: [815] Gézoo, 2012-05-08 11:20:58 |
|
|
| [814] Alma | 2012-05-08 10:26:13 |
 Igen, de itt gyorsan megjegyzem, hogy az s' mennyiség semmiképp nem interpretálható a koordináta-rendszeremben megtett útként, vagy elmozdulásként.
|
| Előzmény: [813] Gézoo, 2012-05-08 07:26:38 |
|
| [813] Gézoo | 2012-05-08 07:26:38 |
 Valóban! Elcseréltem. Ügyes vagy, hogy észrevetted!
A Te rendszeredben mért (számított) mérési adatok a vesszős, a járda rendszere a vessző nélküli. Azaz helyesen így kellett volna jelölnöm: t=t'/sin(arccos(v/c)) időszakasz hosszot.
Hiszen így jelöltük a te rendszeredben mérhető járda hosszot is: s'=s*sin(arccos(v/c)) a járda rendszerében mérhető s hosszból.
Tehát van két adatod, amit mértél, számítottál: s' és t'
és van a járda rendszerében két adat s és t.
Eddig egyetértünk?
|
| Előzmény: [812] Alma, 2012-05-07 21:20:39 |
|
|
| [811] Gézoo | 2012-05-07 21:02:44 |
 Nagyszerű!
Na most fogom a stopperemet és végigsétálok v sebességgel ezen az s úton, a kapott t időt mutató stopperemet megállítom.
Te azt figyelhetted meg, mert éppen ott voltál a járda elején az induláskor t=0 időpontban, hogy állok a Te rendszeredben és közben megy a stopperem mutatója, mozog alattam a járda. Ebből arra gondolsz, hogy én nyugvó vagyok a Te rendszeredben? Ha így van, akkor jól gondolod. Arra gondolsz, hogy a stopperem a Te rendszeredben nyugodva a Te rendszeredben érvényes időt mutatta? Ha így van, akkor ezt is jól gondolod.
Na most a járdán nyugvó óra vajon mit mutatott amikor a járda végére léptem és ettől megállt?
Jól tippelek ha azt mondom, hogy szerinted a járdán nyugvó óra
ami akkor indult el amikor a járdára léptem és akkor állt meg amikor a járda végére érkeztem az
t'=t/sin(arccos(v/c)) időszakasz hosszot mutat?
|
| Előzmény: [810] Alma, 2012-05-07 19:42:51 |
|
|




 t'.
t'.