| [840] Zilberbach | 2012-05-10 17:36:36 |
 Én másképpen tudom/hallottam, legalábbis az időre vonatkozóan.
Ikerparadoxon: az ikerpár gyorsan utazó tagja fiatal marad, míg az itt maradt megöregszik. Nyilvánvaló hogy nem szimmetrikus a viszonyuk az időben.
|
| Előzmény: [839] Alma, 2012-05-10 17:11:29 |
|
| [839] Alma | 2012-05-10 17:11:29 |
 Erre könnyű válaszolni, Gézoonak viszont csak később tudok a vizsgám miatt.
Természetesen mindkét koordinátarendszerből nézve a másik rendszer mérőrúdja megrövidül. Ugyanez érvényes az időkre is, ugyanolyan módon változnak. Teljesen szimmetrikus a két rendszer. Mondok egy analógiát.
Vegyél két közös origóval rendelkező euklideszi koordináta-rendszert, melyek egymáshoz képest el vannak forgatva! Mindkét rendszer x tengelyén vegyél fel egy L hosszúságú szakaszt. Ha a két szakaszt levetíted a másik koordináta-rendszer x tengelyére, mindkét esetben rövidülést tapasztalsz.
Na, specrelben ugyanez van, csak nem euklideszi, hanem minkowski térben. Az effektus lényege ugyanaz.
|
| Előzmény: [838] Zilberbach, 2012-05-10 16:41:42 |
|
| [838] Zilberbach | 2012-05-10 16:41:42 |
 Kezdek kissé összezavarodni.
Szeretnék szóbeli kérdést föltenni Almának és Gézoonak is:
Alább fölvázolok egy viszonylag egyszerű gondolatkísérletet - és annak néhány lehetséges kimenetelét, illetve az abból levonható következtetéseket. Kérem hogy válaszoljatok szerintetek melyik kimenetel, illetve következtetés az "igaz"?
Adott egy S és egy M jelű rendszer. Mindkét rendszerben ugyanazok az eszközök találhatók: egy nagyon pontos mérőrúd, úgy kialakítva, hogy a szomszédos rendszerből is jól és pontosan mérhető legyen (ezt nem is olyan egyszerű megoldani, ábra is tartozna hozzá de sajnos nem tudok ábrát rajzolni) és a szomszédos rendszer mérőrúdjainak hosszúságmérésére alkalmas eszközök. Kezdetben a két rendszer békésen pihen egymás mellett, és a rendszerekben tarózkodó fizikusok megelégedve tapasztalják, hogy mind a saját, mind a szomszédos rendszerekben lévő mérőrudak hossza pontosan 1 méter. Ezután az M rendszer gyors mozgásba kezd, és relativisztikus sebességet ér el (legyen mondjuk: 0,8 c). Ezzel a nagy sebességgel húz el a nyugalomban maradt S rendszer mellett - olyan közelségben, hogy mindketten újra megmérhessék a szomszédos rendszer mérőrúdjának hosszát.
A (fontosabb) lehetséges kimenetelek:
1.) Mindkét rendszerben az Einstein képletei által jósolt rövidüléseket mérik a másik rendszer mérőrúdjain.
Lehetséges logikai következtetés(ek):
A.) a rövdüléseket a sebességkülönbség okozta mérési zavar okozza, és nem a Lorentz-kontrakció - ami ezek szerint valójában nincs is. Az 1. lehetőség bekövetkezéseskor ez a valószínűleg helyes magyarázat. Mindkét rendszer egyenértékű a hosszúság kontrakció szempontjából (is?). (Az egyenértékűség nem is olyan nyilvánvaló, ugyanis az idő lassulása szempontjából a két rendszer nem egyenértékű: az idő lassulása ugyanis csak a gyorsított M rendszerben következik be, és csak az A rendszerből nézve, az M rendszerből nézve viszont az A rendszerben fölgyorsul az idő folyása.)
B.) az M rendszerben gyorsítása miatt valóban történt hosszkontrakció, de emellett még olyan mérési zavarok is kialakulnak, amik azt okozzák, hogy M-ből is - pont ugyanolyan mértékben - rövidebbnek mérik A-rendszer méterrúdját, és a mérési zavarok olyan jellegűek, hogy a megrövidült mozgó méterrúdjukkal is rövidültnek mérik az M rendszer méter-rúdját. Hát ezt nehéz józan ésszel elképzelni, hogy tényleg így legyen, de elvileg ez a lehetőség is fönnáll, ekkor a két rendszer több szempontból sem egyenértékű, nem szimmetrikus a mérési torzulásokra.
2.) Mindkét rendszerben pontosan 1m hosszúnak mérik a másik rendszer méter-rúdjait (is).
Lehetséges logikai következtetés(ek):
A.) nincs hosszkontrakció, nincsenek sebbesség okozta mérési zavarok. Ez igencsak valószínűtlen és erősen ellentmondana Einstein megállapításainak.
B.) az M rendszerben gyorsítása miatt történt hosszkontrakció, de emellett még olyan mérési zavarok is kialakulnak, amik ezt pontosan kompenzálják - nem valószínű, hogy így lenne.
3.) S-rendszerből rövidültnek mérik M-rendszer méter-rúdját viszont M-rendszerből hosszabbnak mérik S-rendszer méter-rúdját.
Lehetséges logikai következtetés: A Lorentz-kontrakció valóban, "fizikailag" lezajlik, mérés okozta torzulások viszont nincsenek.
Tovább is van (lenne) mondjam még? Nem ragozom tovább. A válaszokat előre is köszönöm.
|
|
| [837] Gézoo | 2012-05-10 05:45:06 |
 Kedves Alma!
"Kíváncsi lennék, hogy az s/t mennyiséget hogy értelmeznéd egy olyan mozgó koordinátarendszerben, melyben a járda és az eredetileg mozgást végző test is mozgást végez. "
Nagyon érdekes felvetés!
Áll a bakter a sín mellett és nézi, ahogy az elhaladó vonaton sétáló ember ruháján mászik egy szentjánosbogár.
És arra kíváncsi, hogy a vonat rendszeréből, hogyan látszik a szentjánosbogár.
Ami arra világít rá, hogy hogyan jelöljük a specrelben az egyes inercia rendszereket és a hozzájuk tartozó mérési értékeket.
Szuper! Nyilván tanultad, hogy a szentjánosbogárnak saját sebessége van abban a rendszerben ahol a bakter nyugszik. Saját sebessége van a vonat rendszerében és az emberhez rögzített rendszerben is.
Tehát adva van négy rendszer ebből három rendszer mozog a bakterhez képest.
A négy rendszer mindegyikéből a másik három rendszer 6-6 azaz összesen 24-féle képpen sorba rendezhető.
Azaz négy rendszer lehet aposztróf nélküli jelöléssel, és mindegyikhez 6-6 variációban ', '', és ''' aposztróf rendelhető a' szerint, hogy melyikből nézzük a többieket, illetve melyik a következő a láncban.
Így, a láncba fűzött rendszereknek az egymáshoz viszonyított sebességei attól függenek, hogy a 24 variáció melyikét alkalmazzuk. (Természetesen még több láncolt rendszer esetében a variációk száma sokszorozódik.)
Ugyanis más lesz a bogár és az ember közötti relatív sebesség a vonat, más a bakter és más a bogár vagy az ember rendszeréből mérve.
Tehát az így alkalmazott aposztróf indexek esetében valóban nem invariáns sem a sebesség, sem a Z, sem a 
Remélem belátod, hogy igazából a kezdeti ellenkezésednek nem az lett volna az alapja, hogy nem azzal a formulával számoljuk a hosszkontrakciót vagy az idődilatációt, hanem az alkalmazott aposztrófos jelölés mást jelent.
És így valóban nem invariáns egyetlen paraméter érték sem.
Ez viszont felveti egy másik problémát.
Ugyanis a mindenkori v sebességet v=c/n alakban megadva, az n állandósága mellett v csak úgy lehet változó értékű, ha c is változó értékű. Ez is és a  =c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának. =c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának.
Másik oldal viszont az, hogy a felsorolt invariancia lehetőségek mindegyike valóban invariáns közvetlen páronként, azaz
K-K1', K-K2', K-K3', .. , K-Kn' esetén.
|
| Előzmény: [836] Alma, 2012-05-09 23:03:54 |
|
| [836] Alma | 2012-05-09 23:03:54 |
 Ha jól értem a szép hosszú hozzászólásodban azt írtad le, hogy álló forrás által keltett sugárzás (transzformált) hullámhosszát megmérve mozgó koordinátarendszerben (ismervén a rendszer sebességét is), meghatározható a forrás nyugalmi rendszerbeli frekvenciája (ez egyébként nem is igaz, mert ismerni kell a sugárzás terjedési irányát is, de most nem akarok a 3D-vel kötekedni)
Te az invariáns szót kicsit furcsán használod egyébként. Akkor nevezünk (Lorentz) invariánsnak valamit, ha a (Lorentz) transzformáció invariánsan hagyja. Ehhez semmiféle átdefiniálgatásra nincs szükség, nem kell c° és egyéb kompenzáló mennyiségeket bevezetni.
Kíváncsi lennék, hogy az s/t mennyiséget hogy értelmeznéd egy olyan mozgó koordinátarendszerben, melyben a járda és az eredetileg mozgást végző test is mozgást végez.
Vagyis, definiáld kérlek az s'' és t'' mennyiségeket egy u sebességgel mozgó rendszerben úgy, hogy s'' / t''= s/t fennálljon!
|
| Előzmény: [835] Gézoo, 2012-05-09 15:40:51 |
|
| [835] Gézoo | 2012-05-09 15:40:51 |
 Kedves Alma!
"Testnek neveztem azt, ami a te rendszeredben mozog. "
Ami a járda rendszerében azzal a v sebességgel mozog, amely v sebesség van a két rendszer koordináta rendszereinek origói között, az a test a te rendszeredben nyugvó (álló), a sebessége nulla. Nyilván a járda mint test mozog a te rendszeredben, így a járda v sebességéről és a te rendszered valamely pontján való járda hossz (s'=s*ß) áthaladásának t' idejéről beszélhetünk áthaladási időként, és nem a te rendszeredben nyugvó test áthaladási idejéről, mert a nyugvónak nincs olyan ideje.
"A járdának van sebessége, meg is mondtam, hogy mennyinek gondolom, s'/t', ahogy te is."
Nagyon jó! Így van! Egyetértünk!
******* ******** ******** ******* ********
Ha jól látom, akkor alaposan körbejártuk ezt a témát. És bár, első ránézésre eretnek gondolatnak tűnt számodra a Z=s*t=s'*t' invariánskénti tálalása, a v sebesség "invarianciájának" egy fajta "szinonimájaként" felfogva, csak szokatlan, de éppen úgy invariáns.
A régi görög filozófusok felvetették azt a lehetőséget, hogy amikor kilövünk egy nyilat, akkor a nyíl, sok kis nyilacska sorozataként halad előrefelé.
Ilyen értelmezésben az időegységre eső útszakaszt a sebesség helyett az ismétlődési ütemmel, azaz a frekvenciával is jellemezhetjük.
Vagyis ha a hossz mércéje például egy adott frekvenciájú fényforrásból kilépő fény "f" frekvenciája, akkor a sebesség helyett ezzel is leírható lenne a hossz és az idő viszonya:
s=c°*t' alakban.
Nézzük azt is meg, hogy mit és miért jelöltem ezekkel a jelekkel:
Az f frekvenciájú fényt sugárzó fényforrás nyugodjon K rendszerben. Legyen egy v sebességgel mozgó K' rendszerben a megfigyelő aki így f' frekvenciának méri: f'=f*gyök((v+c)/(v-c)) függvény szerint (rel.Doppler) a fény frekvenciáját - közeledő 1D-s esetben -. Ha ez a K' rendszerben nyugvó megfigyelő képezi a "virtuális" c° sebességet: c°=c*gyök((v+c)/(v-c)) függvény segítségével, akkor az eredeti f frekvencia és Hertz függvényének - c=f* - felhasználásával az eredeti - felhasználásával az eredeti  hullámhossz: hullámhossz:  =c°/f' értéke megegyezik a forrás rendszerében lévő =c°/f' értéke megegyezik a forrás rendszerében lévő  =c/f hullámhossz értékével. =c/f hullámhossz értékével.
És miután az f' frekvenciára érvényes, hogy
f'=1/t'
így  =c°*t' alakkal a megmért t' periódusidővel és a "virtuális" c° fénysebességgel közvetlenül megkapjuk a forrás rendszerében mérhető =c°*t' alakkal a megmért t' periódusidővel és a "virtuális" c° fénysebességgel közvetlenül megkapjuk a forrás rendszerében mérhető  hullámhosszot. hullámhosszot.
Ha pedig ezt a  ; hullámhosszot a forrás rendszerében távolság, illetve hossz mérésre használtuk, akkor a K' rendszerben mért t' periódus idővel közvetlenül mérhetjük a forrás rendszerében lévő távolságokat. ; hullámhosszot a forrás rendszerében távolság, illetve hossz mérésre használtuk, akkor a K' rendszerben mért t' periódus idővel közvetlenül mérhetjük a forrás rendszerében lévő távolságokat.
Például t=1/3e8 [s] esetében a  =1 [m] és v=0,8c rendszerben ezzel c°=c*3 (v=0,8c esetében a gyök((v+c)/(v-c))=3 ) =1 [m] és v=0,8c rendszerben ezzel c°=c*3 (v=0,8c esetében a gyök((v+c)/(v-c))=3 )
Azaz a megmért t'=1/9e8 [s] periódusidővel a forrás rendszerben lévő hosszok:  =c°*t'=9e8/9e8= 1 [m] azaz a forrás rendszerében mérhető hullámhosszal azonos hossz. =c°*t'=9e8/9e8= 1 [m] azaz a forrás rendszerében mérhető hullámhosszal azonos hossz.
Miután minden v értékkel ugyanezt a  =1 [m] -t kapjuk a forrás rendszeri =1 [m] -t kapjuk a forrás rendszeri  =1 [m] hullámhossz esetében, elmondható, hogy a "virtuális" c° fénysebesség használatával a =1 [m] hullámhossz esetében, elmondható, hogy a "virtuális" c° fénysebesség használatával a  =c°*t'=v°*t' szintén invariáns. =c°*t'=v°*t' szintén invariáns.
Végezetül megemlítem, hogy ezek a gondolatok vélhetően éppen úgy szokatlanok a számodra mint az elsőként említett Z=s*t=s'*t' invariáns.
|
| Előzmény: [834] Alma, 2012-05-09 14:52:02 |
|
| [834] Alma | 2012-05-09 14:52:02 |
 Testnek neveztem azt, ami a te rendszeredben mozog. A járdának van sebessége, meg is mondtam, hogy mennyinek gondolom, s'/t', ahogy te is.
|
| Előzmény: [833] Gézoo, 2012-05-09 13:14:05 |
|
| [833] Gézoo | 2012-05-09 13:14:05 |
 Tehát a járda s' (azaz s'=s*ß rövidült "állapotban" :) ) hosszának egyik vége érkezzen be a Te rendszered egy pontjára t'=0 időpontban és méred az áthaladás idejét t'>0 értéket kapsz. Nyilván az v'=s'/t' a mozgó járda egy pontjának a Te rendszeredben mért sebességét adja..
"De attól, hogy van egy hosszúságadatom, és van egy időadatom, attól a hányadosuk nem lesz a test sebessége a rendszeremben."
Hogy érted, hogy ez a sebesség nem a járda sebessége a Te rendszeredben?
|
| Előzmény: [832] Alma, 2012-05-09 12:55:43 |
|
| [832] Alma | 2012-05-09 12:55:43 |
 Nem értek egyet. Mint már többször mondtam, az én rendszeremben nem mozog a vizsgált test, nulla a sebessége és nulla a megtett út.
A te rendszeredben nyugalomban lévő járda hossza az én rendszeremben
s'=s*sin(arccos(v/c)).
Ezzel egyetértek. Ha végigsétálsz a járdán, a mozgás idejét én, az én rendszereben megmérve ha t' értéket kapok, akkor az, a te rendszeredben
t=t'/sin(arccos(v/c)
időtartam lesz. Ezzel is egyetértek. Így definiálva a mennyiségeket még s/t=s'/t'-vel is egyetértek.
De attól, hogy van egy hosszúságadatom, és van egy időadatom, attól a hányadosuk nem lesz a test sebessége a rendszeremben. Abban a trivialitásban megegyezhetünk, hogy a te rendszeredben a test ugyanakkora sebességgel halad, mint az én rendszeremben a járda halad visszafelé.
|
| Előzmény: [831] Gézoo, 2012-05-09 12:42:23 |
|
| [831] Gézoo | 2012-05-09 12:42:23 |
 Nagyon jó! Szóval hogy is van ez? a Te rendszered a K' rendszer az s' és t' mérési adatokkal, járda rendszere a K rendszer s és t adatokkal.
A Te rendszeredben mértünk s'=s*ß hosszon áthaladás alatt, t' időt, vagyis v'=s'/t' sebességet.
A járda rendszerében v=s/t
A két v=v' egyenlő nagyságú. (Bár nem szokás v' jelölés, mert az egyenlőség léte alapfelvetés.)
Így egyetértünk?
|
| Előzmény: [828] Alma, 2012-05-09 12:21:07 |
|
|
|
| [828] Alma | 2012-05-09 12:21:07 |
 Álljon meg a menet, kezdesz ködösíteni. Világosan fogalmazz! Írd le, hogy szerinted az
s*z=s'*z'
egyenletből hogyan következik az
s/z=s'/z'
egyenlet, mert ez nem puszta matematikai átalakítás.
Megjegyezném, hogy az én, mozgó rendszerem t' idejét projektáltad át a járdához rögzített rendszerbe, vagyis helyesen az idődilatáció:
t=t'/sin(arccos(v/c),
mint ahogy ezt korábban közösen elfogadtuk. Ebből következően az utána levő levezetésed hamis.
|
| Előzmény: [827] Gézoo, 2012-05-09 10:24:24 |
|
| [827] Gézoo | 2012-05-09 10:24:24 |
 Jól mondod.. Ez a lényeg.
Az invariencia fennmarad akár s'/t' akár s'*t' a végzett művelet.
Sőt!
s'=s*sin(arccos(v/c)) és t'=t/sin(arccos(v/c) függvények tovább erősítik ezt a megállapítást.
Hogy még szemléletesebb legyen éljünk b=sin(arccos(v/c) alakkal: s'=s*b és t'=t/b
azaz a kérdés, hogy s*t egyenlő-e s'*t' szorzattal?
végezzük el a műveletet s'=s*b és t'=t/b egyenlőségeket felhasználva s*t ?=? s*b*t/b
átrendezve:
s*t ?=? s*t* b/b ahol b/b=1 ott
s*t=s*t eredményt kapunk, tehát ha
s/t=s'/t' invariáns akkor s*t=s'*t' szintén invariáns
|
| Előzmény: [826] nadorp, 2012-05-09 08:59:25 |
|
| [826] nadorp | 2012-05-09 08:59:25 |
 Bocs, hogy beleszólok. Előre bocsátom, hogy a relativitáselmélethez nem értek, és ha hülyeséget írnék, már most meggyónom :-). Az nem világos, hogy itt a matematika szabályai "felborulnak"? Gondolok arra, hogy 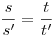 és az állítás szerint a jobb oldal invariáns a reciprok képzésre. De ez nem igaz, mert reciprokot véve a jobb oldal és az állítás szerint a jobb oldal invariáns a reciprok képzésre. De ez nem igaz, mert reciprokot véve a jobb oldal  lesz. Más analógiát véve, ha veszünk egy háromszöget, aminek két oldala a,b, akkor a hozzá hasonló háromszögek közt az lesz. Más analógiát véve, ha veszünk egy háromszöget, aminek két oldala a,b, akkor a hozzá hasonló háromszögek közt az 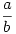 mennyiség invariáns lesz, de ab nem lesz az. Vagy a fentiek nem húzhatók rá a szóban forgó példára? mennyiség invariáns lesz, de ab nem lesz az. Vagy a fentiek nem húzhatók rá a szóban forgó példára?
|
| Előzmény: [825] Gézoo, 2012-05-09 07:08:34 |
|
| [825] Gézoo | 2012-05-09 07:08:34 |
 Nagyszerű!
Tehát, ha s*z = s'*z' invariáns, akkor t=1/z alakkal behelyettesítve is invariáns, mivel csak a reciprokáról van szó s*(1/z)= s'*(1/z')
Vagy szerinted van oka annak, hogy a reciprokkal elveszítjük az invarienciát mint tulajdonságot?
|
| Előzmény: [824] Alma, 2012-05-08 21:47:23 |
|
|
| [823] Gézoo | 2012-05-08 21:05:16 |
 Nos, jó. Egyszerűsítsünk!
s/t=s'/t' ebben egyetértettünk, akkor ezzel ebben is:
s * (1/t) =s'* (1/t')
vagy akár z=1/t behelyettesítéssel ebben is:
s*z = s'*z'
Jól gondolom?
|
| Előzmény: [822] Alma, 2012-05-08 15:58:25 |
|
| [822] Alma | 2012-05-08 15:58:25 |
 t2*s/t=t'2*s'/t' miért lenne igaz, ha s/t=s'/t'? t t'. t'.
|
|
|
|
|
|
| [817] Gézoo | 2012-05-08 11:40:30 |
 Tehát ha jól értelek, akkor szerinted is érvényes:
v = s/t = s'/t' ?
:D Na akkor szorozzuk meg egy t2 -el minden tagot!
Az egyenlőség nem változhat,
v * t2 = t2*s/t = t'2*s'/t'
Eddig érthető?
|
| Előzmény: [816] Alma, 2012-05-08 11:26:56 |
|
| [816] Alma | 2012-05-08 11:26:56 |
 Pontosan, így gondolom. Az én koordináta-rendszeremben, mint megállapodtunk, a tiedben mozgó test áll, 0 a sebessége.
Az én rendszeremben mozog a járdád, így kerül arrébb a test a járdához képest. Nem a testnek van sebessége, hanem a járdának. Ha kettőnk közötti koordináta-rendszert vennénk, akkor még bonyolultabb lenne a helyzet, hiszen akkor a járda és a test is mozogna, valamint a járda nyugalmi hossza is kontraktálódna természetesen.
|
| Előzmény: [815] Gézoo, 2012-05-08 11:20:58 |
|




 =c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának.
=c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának. 
 t'.
t'.