|
|
| [857] Gézoo | 2012-05-12 10:51:41 |
 Kedves Zilberbach!
Valóban, a specreles időlassulásra szokás példaként emlegetni.
Nos, a fizikai jelenség létező. Csak hogy a Föld gravitációs mezejében v=0,999c és v=0,9999c közötti sebességű részecskékkel.
Amik tetejében h=1e4 m magasságról érkeznek a felszínre
azaz a gravitációs időlassulás t=t0/(1-g*h/c2) értékét mint álló test érzékelné a részecske.
csakhogy rel.Dopplerrel "sűrűbb" számára a gravitációs mezőt alkotó sugárzás.
faktor=((c+v)/(c-v))(1/2) Ez, v=0,9999c esetében faktor=((1,9999)/(0,0001))(1/2)=141
vagyis t=141*2e-6/(1-10*1e4/9e16)=0,000282 [s]
s=3e8*0,000282=84'600 [m]
Tehát a gravitációs időlassulás és a rel.Doppler együttes hatása nem csak a feltételezett 10 km-ről leérkezést, hanem 84,6 km magasról leérkezéshez elegendő időlassulás eredményez.
Vagyis nincs szükség az ikerparadoxon létezésére.
Sőt! Ha e mellé a gravitációs időlassulás mellé még az ikerparadoxon is létezőként hatna, akkor a müonok sokkal kisebb sebességgel is elérhetnék a felszínt.
Amikor ilyeneket olvasol mindig jusson eszedbe, hogy Einstein életében nem volt, nem létezett űrhajó. Minden feltételezése (posztulátum = bizonyítás, igazolás nélkül elfogadandó feltételezés!) csupán egy olyan világban született ember feltételezése volt, amely világban mobil telefon, számítógép, TV, lézer, űrhajó nem volt. A repülés is léghajó szinten "működött" éa világszenzációnak számított 1909-ben a La manche azaz a csatorna átrepülése is.
Vonatokon utazgatva szemlélte a relatív mozgásokat.
Fel sem merülhetett benne, hogy valaha majd például én a számlálós módszerrel bemutatom az ikerparadoxon lehetetlenségét.
|
| Előzmény: [856] Zilberbach, 2012-05-12 09:23:18 |
|
| [856] Zilberbach | 2012-05-12 09:23:18 |
 Kedves Gezoo!
Hogyan magyarázható az iker-paradoxon egyik régen sokat emlegetett és sokszor kimért bizonyítéka:
A föld légkörének fölső rétegében 2 mikroszekundum - azaz nagyon rövid átlagos élettartamú - µ-mezonok keletkeznek, a kozmikus sugárzás hatására. 2 mikro-szekundum alatt még fénysebességgel is csak 650 méter utat tudnak megtenni. Mégis lejutnak a földfelszínig, és jól mérhetők. Ezt (régebben) csak azzal tudták magyarázni, hogy ezekben a nagyon gyors mozgású µ-mezonokban lelassul az idő múlása, és ezért nem bomlanak le a kb. 20-30 km-es úton - tehát az iker-paradoxon létezik és működik. Mi akkor erre a jelenségre a magyarázat, ha nem az iker-paradoxon? Ráadásul ezek a részecskék gyorsan közelednek a mérő-műszerekhez és nem távolodnak, tehát a 845.sz hozzászólásodban említetteknek megfelelően számunkra inkább gyorsultnak tűnik benne az idő.
|
| Előzmény: [845] Gézoo, 2012-05-10 18:50:20 |
|
| [855] Gézoo | 2012-05-12 08:05:12 |
 A javaslom a "tehetetlenség" és a "tehetetlen tömeg" kifejezéseket tartalmi eltérésük miatt különböztessük meg.
A tehetetlenség a tömeg nagyságához köthető fogalom. A lendület mértékét a tömeg és a relatív mozgásának sebessége képezi. Ezért a nagysága függ a tömeg nagyságától és attól a relatív sebességtől ami a kölcsönható és a tömeg között van:
I=m*v alakban.
"Rokona a mozgási energiának, amely szintén a tömeg nagyságától és a kölcsönhatónak a relatív sebességtől függ:
E=(v/2)*I = (v/2)*m*v = (1/2)*m*v2)
Amely összefüggésben azért nem E=m*v2 hanem csak a fele szerepel, mert a másik fele a kölcsönható oldal energiája.
Azaz legyen két, egyforma tömeg egymás mellett, és az egyikre ülve (nekünk legyen nulla a tömegünk a példa átláthatósága kedvéért,) elrúgjuk a másik tömeget.
Ezt egy külső szemlélő úgy látja, hogy az elrúgás helyétől mindkét tömeg azonos sebességgel és ezzel azonos lendülettel (azaz impulzussal) és ezzel azonos energiával távolodik.
Vagyis a befektetett energia egyik felét az egyik, másik felét a másik tömeg vitte magával. Ezért felezzük meg a mozgási energiát amikor csak az egyik tömeget látjuk mert tudjuk, hogy annak a félnek a sebessége ill. az energiája csak fele a mozgását létrehozó teljes energiának.
Ezekből következően a lendület megváltoztatásához a tehetetlenség ellenében a tömeg nagyságával és a sebesség változtatás felével egyenesen arányos mennyiségű energiát kell befektetnünk.
Ami egyben arra is rámutat, hogy a v sebességgel mozgónak a mozgási irányában két oldalon nem azonos a kölcsön ható képessége. Hátulról ugyanis ahhoz, hogy hathassunk rá, "utána kell futnunk", ami közben elölről elég elé állnunk.
(Azaz az utána futás létrehozásának energia igényét negatív energiának tekintve - mert ezt befektettük, azaz a kölcsönhatásból kapott energiából le kell vonni az egyenleg képzésekor - a tehetetlenség "hátulról" értelmezhető határolt negatív energiájúnak is, ahol a határ az utolérés energia igénye.)
Sőt! Még akkor is hat ránk, ha a sebességénél kisebb sebességgel haladunk előtte. Ekkor például a két sebesség különbségének nagysága adja azt a lendület és energia értéket amit a hatásban érzékelünk.
Ilyen értelemben a tömeg nagyságát a tehetetlenségének mértékeként is szokás definiálni.
A tehetetlenség okaként az égre-földre keresett Higgs bozont és a Higgs mezőt teszik felelőssé.
De ez csak egy elv. Aminek az érvényességét eddig nem sikerült igazolni.
Van sok más elv is.
Egyik az a spinfoton sugárzás elvén alapuló amit ebben a topicban korábban leírtam.
Ha visszalapozol a levezetéssel együtt megtalálod. Minimum gondolat ébresztőnek szánva érdemes elolvasnod.
|
| Előzmény: [854] Zilberbach, 2012-05-11 22:27:01 |
|
|
| [853] Zilberbach | 2012-05-11 22:11:55 |
 A véleményed tehát az, hogy (egyenletes sebesség esetén) mindkét rendszerből ugyanazt mérik, a másik rendszerre vonatkozóan. Ha jól értem akkor azt, hogy a tehetetlen tömeg az Einstein szerint jósoltakkal egyezően nő, a gravitáló tömeg viszont nem.
|
| Előzmény: [850] Gézoo, 2012-05-11 17:23:37 |
|
| [852] Zilberbach | 2012-05-11 22:10:14 |
 A véleményed tehát az, hogy (egyenletes sebesség esetén) mindkét rendszerből ugyanazt mérik, a másik rendszerre vonatkozóan. Ha jól értem akkor azt, hogy a tehetetlen tömeg az Einstein szerint jósoltakkal egyezően nő, a gravitáló tömeg viszont nem.
|
| Előzmény: [850] Gézoo, 2012-05-11 17:23:37 |
|
| [851] Gézoo | 2012-05-11 17:38:37 |
 Amikor Einsteinnek és kortársainak a gondolkodását, elméleteit nézzük, ne feledjük el azt a kort sem amiben ők felnőttek és éltek.
Amikor Einstein megszületett, akkor még minden csillagász esküdött arra, hogy a világ egyetlen galaxisból áll. A relativitás elméletének megjelenése után 4 évvel repülté át először a La manche-t azaz a csatornát. És az első űrhajó Einstein halála után öt évvel vitte fel Gagarint..
Nyilván nem gondolkodhatott olyan lehetőségek létezésében amiket azóta valósított meg az emberiség. A kisfiam amikor Napóleonról tanult és a csatái kerültek szóba azt kérdezte, hogy miért nem hívta fel telefonon Wellington hercegét. Annyira ebben a korban élve, fel sem merült benne, hogy akkor még egy üzenet továbbítása lóval napokba vagy esetenként hónapokba tellett.
|
| Előzmény: [850] Gézoo, 2012-05-11 17:23:37 |
|
| [850] Gézoo | 2012-05-11 17:23:37 |
 Nagyon jó felvetés!
A tömeg tehetetlenségét kölcsönhatás hiányában számolással, a relatív energiájának a számításával végezhetjük el. Ez az ütköztetéses próbákkal igazoltan jó számítás Einstein 1905-ös specreljéből másolva: 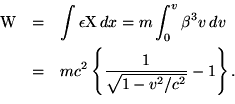
Viszont az M tömeg gravitáló hatását így nem tudjuk ellenőrizni. Ezért az "elsuhanáskor" a melléhelyezett órák lassulásából t=t0/(1-GM/h'/c2)/sin(arccos(v/c)) függvénnyel megmérhetnénk.
Igen ám, de idő lassulást nem tudott eddig senki sem kimutatni állandó (egyenletes) sebesség esetében.
Azaz ezt azt jelenti, hogy az egyenletes sebességű rendszerekben nyugvó testek tömege nem változik. Viszont a mindenkori energiájukat a mozgási és a tömegben tárolt ( E=m*c2 ) energiáik összege szerint, azaz a mozgási energiák növekedésével az idézett függvény szerint változik.
Ismét meg kell említenem, hogy az egyenletes sebességű mozgásnál mindkét oldal szimmetrikusan ugyanazt mérheti. (Azaz az egyik ugyanazt mint a másik oldal.)
A kérdésed lényegét tekintve, biztosan láttál már autómérleget. (A tüzépekben a teherautók megmérésére szolgáló "túlméretes mázsa".) Ha ezen megy neki az odakészített betonfalnak egy autó, olyan esetben amikor csak 1km/h sebességgel haladt és olyan esetben is amikor 100 km/h sebességgel haladt, akkor a mérleg nem fog különböző tömeget mérni. Pedig az első esetben csak a lökhárító deformálódik, a második esetben ripityára törik az autó.
Azaz nem a gravitáló azaz súlyos tömege, hanem csak a lendülete volt különböző a két esetben.
|
| Előzmény: [849] Zilberbach, 2012-05-11 14:09:11 |
|
| [849] Zilberbach | 2012-05-11 14:09:11 |
 Adott egy S és egy M jelű rendszer. Mindkét rendszerben ugyanazok az eszközök találhatók: egy 1 kilogramm tömegű etalon test, és a pontos (táv)mérésére szolgáló műszerek. Kezdetben a két rendszer békésen pihen egymás mellett, és a rendszerekben tartózkodó fizikusok megelégedve tapasztalják, hogy mind a saját, mind a szomszédos rendszerekben lévő etalon testek tömege pontosan 1 kilogramm. Ezután az M rendszer gyors mozgásba kezd, és relativisztikus sebességet ér el (legyen mondjuk: 0,8 c). Ezzel a nagy sebességgel húz el a nyugalomban maradt S rendszer mellett - olyan közelségben, hogy mindketten újra megmérhessék a szomszédos rendszer etalon-testeinek tömegét. Mi lenne a mérések kimenetele?
1.) Mindkét rendszerből 1 kg-nál nagyobb tömegűnek mérnék a másik rendszer etalon-testét?
2.) A nyugalomban maradt S rendszerből 1 kg-nál nagyobb tömegűnek mérnék a 0,8 c sebességgel mozgó M rendszer etalonját, viszont M rendszerből 1 kg-nál kisebb tömegűnek mérnék az S rendszer etalonját?
3.) Valami más kimenetele lenne a a méréseknek.
A sejtésem az, hogy az 1.) a jó válasz. Ha így van, akkor mi az oka ennek - a valójában csak a mérés tökéletlen kivitelezhetőségéből adódó - látszat tömegnövekedésnek?
|
|
|
|
| [846] Gézoo | 2012-05-10 19:35:41 |
 :) Hát igen. Nagy kérdés, hogy milyen tudásszintűknek szól a könyv. Az sem hátrány, ha az előadó alaposan ismeri nem csak az adott tananyagot, hanem azt is, hogy a benne állókhoz milyen út vezetett. Mindent megértettél? Van még kérdésed?
|
| Előzmény: [844] Zilberbach, 2012-05-10 18:49:51 |
|
| [845] Gézoo | 2012-05-10 18:50:20 |
 Az ikerparadoxonban csak addig látszik fiatalabbnak a másik amíg fennáll a relatív sebesség. Ugyanis az öregedésről tudósító fény késve érkezik a  szögű terjedés következtében. szögű terjedés következtében.
Az a magyarázatok külön hibája, hogy a Földön maradt testvér öregszik jobban, mert a fizikai valóságban pont fordított a helyzet ha a távozó testvér rövid ideig ható gyorsulással éri el az utazási sebességeit.
Ugyanis a Föld gravitációjában lassabban múlik a idő mint az űrben az űrhajó parányi (1e-24 -szeres ) gravitációjában.
Tetejében mindkét testvér fiatalabbnak látja a másikat a távolodás idején mint saját magát.
Ezt úgy lehet a legkönnyebben megérteni, ha mindkét testvér órájának lépését (időalap léptetését) egy-egy villanás kíséri és ezeket a villanásokat a másik tesó is érzékeli.
Azt biztosan tudod, hogy a rel. Doppler torzítja el a beérkező villanások ütemét, de a villanások darabszámát se a Doppler, se a relatív mozgás nem tudja megváltoztatni.
Azaz a távolodáskor például v=0,8c sebesség esetében az órajelek frekvenciája
f=f0*gyök((c-v)/(c+v)) sebességre lassulnak látják egymást: azaz f=f0/3 a v=0,8c esetében.
Vagyis amíg távolodnak egymástól, mindkettő a másik óráját és minden folyamatát 1/3 járási sebességre lassultnak látja. Ezzel az öregedését is.
Visszafelé úton pedig mindkettő a másik óráját f=f0*gyök((c+v)/(c-v))=3*f0 azaz háromszor gyorsabban ketyegőnek látja mint a saját óráját.
Miután minden villanást mindkét óránál megszámolunk, így egymás mellé érve mindkét óra ugyanazon villanásszámot mutathatja, semmi mást.
:) Nem veszhetnek el villanások egyiküknél sem. Azaz nem vesznek el a lassulás és a gyorsulás ellenére sem másodpercek egyikük idejéből sem.
Összefoglalva:
Az ikerparadoxon egy geometria, rossz és nagyon hibás alkalmazásával kapott hibás számítási eredmény.
|
| Előzmény: [840] Zilberbach, 2012-05-10 17:36:36 |
|
|
| [843] Gézoo | 2012-05-10 18:13:54 |
 Az idő..
Nos, az idő meg se moccan. Sőt! Einstein az idő helyett az órákat emlegeti. Azaz azt, hogy mit mutatnak az órák.
Ha láttad az előző ábrát, elolvastad azt is, hogy a mozgás irányára merőleges ordináta  =arccos(v/c) szöggel hátra hajlott, akkor nyilván beláthatod azt is, hogy az óra számlapjáról a megfigyelőhöz a fény nem akkor érkezik amikor a mutató lép, hanem a hátra hajlás szögével később. Ezért ha megszűnik a köztük lévő sebesség akkor azt látjuk, hogy hihetetlen sebességgel "előrepörög" a mutató a megfigyelőnél végig nyugalomban lévő óra mutatója mellé. =arccos(v/c) szöggel hátra hajlott, akkor nyilván beláthatod azt is, hogy az óra számlapjáról a megfigyelőhöz a fény nem akkor érkezik amikor a mutató lép, hanem a hátra hajlás szögével később. Ezért ha megszűnik a köztük lévő sebesség akkor azt látjuk, hogy hihetetlen sebességgel "előrepörög" a mutató a megfigyelőnél végig nyugalomban lévő óra mutatója mellé.
Persze csak Minkowski geometriájában, mert a valóságban a sebesség változás azaz a gyorsulás hatására valóban lelassul minden folyamat, így az óra járása is (1-gh/c2) szorzóval gravitációs gyorsulás esetében és az ezzel egyenértékű mértékben az erő okozta gyorsulás hatására szintén.
Összefoglalva: Az idő nem lassul le, az állandó sebességű relatív mozgás esetében, csak lassultnak látszik, és ezzel lassultnak mérhető.
|
| Előzmény: [841] Zilberbach, 2012-05-10 17:38:51 |
|
| [842] Gézoo | 2012-05-10 17:55:08 |
 Kedves Zilberbach!
Alma jól válaszolt. Mindegy, hogy a gyorsuláson átment, vagy a gyorsulást okozó erőhatás nélkül hagyott rendszerből mérjük a másik rendszerbeli rúd hosszát, ugyanazt az eredményt kapjuk: a saját rúd hosszának sin(arccos(v/c))-szeresének mérhetjük a másik rendszerben nyugvó rúd hosszát.
Ennek oka a mozgás sebességének és a méréshez használt fény sebességének a viszonya.
Minél közelebb van egymáshoz a két sebesség annál inkább hátra hajlottnak látszik a mért rúdról kilépő fény iránya.
Ezzel olyan, mintha a derékszög hátrafelé arc cos(v/c) szöggel hajolna, éppen úgy, mint a képen látható hullámok.
Hogy miért nem a Lorentz féle valós kontrakció lép fel?
Nos, egyszerű! Vegyél kezedbe egy gumira rögzített radírt, vagy más terhet. A gyorsulás alatt a gumi megnyúlik, de a gyorsulást okozó erő megszűnésével visszaáll az eredeti hosszra.
(Mondjuk a gumi pont rossz példa, acélrugó sokkal jobb lenne, mert a gumiban lévő hosszú láncok az erő hatására mindig "megfolynak" azaz átrendeződnek és ezzel a gumi kicsi megnyújtott marad.)
Azaz ha a gyorsulást okozó erőhatás alatt álló méterrúd mellé tennél egy a gyorsulás irányára merőlegesen világító lézer pointert, akkor a gyorsulás kezdetén a fénypontja "hátra maradna" mintha lehajlana a fényútja. De a gyorsulás megszűnésével az eredeti, "nyugalmi állapotába visszaállna a fénypont"
Érdekesség, hogy interferométerben éppen ezt a lehajlást és a megszűnését az interferencia csíkok elmozdulásával ki tudjuk mutatni már pár cm/s2 gyorsulás esetében is.
Az Alma által említett Minkowski  féle geometriával ez a "hátra hajlás" szépen kezelhető. féle geometriával ez a "hátra hajlás" szépen kezelhető.
Amikor anno Einstein előállt a relativitás elméletével 1905-ben, az akkori csillagászok egy része úgy tekintett az elméletre, mint a már akkor több mint 200 éve ismert fényaberráció egyik leírási változatára. Nem véletlen, hogy amikor még csak készült a kézirat, ezt már többen jelezték Einsteinnek és így már a 7.§-ban szerepeltette a Doppler és a fény aberráció "relatív" változatát. Miközben az egész dolgozatának a lényegét, az apropóját jelentő elektrodinamikáról csak a 10.§-ban írt. Ezzel is jelezve, hogy mennyire nagy nyomást jelentett az akkori neve csillagászok véleménye.
Egyébként nem "Einstein jósolta", hanem Lorentz írta le, csak Einstein beépítette. Éppen úgy mint ahogyan az E=m*c2 sem Einstein "találmánya", (bár majdnem mindenki, még a szakkönyvek közül is több úgy írja, ) hanem Lebegyev-nek a műve még 1902-ből. Ezt is csak beépítette Einstein.
Tehát összefoglalva:
A mérőjel (a fény) c sebességének és a mozgást végző test (ill. rendszer) sebességének a gyök(1-(v/c)2) (vagy ahogy még felírható sin(arccos(v/c) praktikusan,) viszonyától függő mértékben látszólag hátragörbült a koordináta rendszer mozgásra merőleges iránya.
Azaz nem fizikai változást, hanem egy minden mérésben benne lévő, a jelenlegi méréstechnikával kikerülhetetlen mérési hiba.
Viszont ez a mérési hiba Feynman fényórájával leírva egy olyan derékszögű sebesség-háromszöget alkot, ami mind addig garantálja ennek a hibának a létezését amíg a mérést végző és a mérés tárgya egymáshoz képest mozog.
Megemlítem, hogy nagyon kicsi sebességeknél is érvényesül ez a hatás, csupán olyan kicsiny eltérést okoz amit egyszerűbb esetekben nem veszünk észre.
|
| Előzmény: [838] Zilberbach, 2012-05-10 16:41:42 |
|
| [841] Zilberbach | 2012-05-10 17:38:51 |
 Javítás: "(Az egyenértékűség nem is olyan nyilvánvaló, ugyanis az idő lassulása szempontjából a két rendszer nem egyenértékű: az idő lassulása ugyanis csak a gyorsított M rendszerben következik be, és csak az A rendszerből nézve, az M rendszerből nézve viszont az A rendszerben fölgyorsul az idő folyása.)
B.) az M rendszerben gyorsítása miatt valóban történt hosszkontrakció, de emellett még olyan mérési zavarok is kialakulnak, amik azt okozzák, hogy M-ből is - pont ugyanolyan mértékben - rövidebbnek mérik A-rendszer méterrúdját, és a mérési zavarok olyan jellegűek, hogy a megrövidült mozgó méterrúdjukkal is rövidültnek mérik az M rendszer méter-rúdját. Hát ezt nehéz józan ésszel elképzelni, hogy tényleg így legyen, de elvileg ez a lehetőség is fönnáll, ekkor a két rendszer több szempontból sem egyenértékű, nem szimmetrikus a mérési torzulásokra."
Helyesen: (Az egyenértékűség nem is olyan nyilvánvaló, ugyanis az idő lassulása szempontjából a két rendszer nem egyenértékű: az idő lassulása ugyanis csak a gyorsított M rendszerben következik be, és csak az S rendszerből nézve, az M rendszerből nézve viszont az S rendszerben fölgyorsul az idő folyása.)
B.) az M rendszerben gyorsítása miatt valóban történt hosszkontrakció, de emellett még olyan mérési zavarok is kialakulnak, amik azt okozzák, hogy M-ből is - pont ugyanolyan mértékben - rövidebbnek mérik S-rendszer méterrúdját, és a mérési zavarok olyan jellegűek, hogy a megrövidült mozgó méterrúdjukkal is rövidültnek mérik az M rendszer méter-rúdját. Hát ezt nehéz józan ésszel elképzelni, hogy tényleg így legyen, de elvileg ez a lehetőség is fönnáll, ekkor a két rendszer több szempontból sem egyenértékű, nem szimmetrikus a mérési torzulásokra.
|
| Előzmény: [838] Zilberbach, 2012-05-10 16:41:42 |
|
| [840] Zilberbach | 2012-05-10 17:36:36 |
 Én másképpen tudom/hallottam, legalábbis az időre vonatkozóan.
Ikerparadoxon: az ikerpár gyorsan utazó tagja fiatal marad, míg az itt maradt megöregszik. Nyilvánvaló hogy nem szimmetrikus a viszonyuk az időben.
|
| Előzmény: [839] Alma, 2012-05-10 17:11:29 |
|
| [839] Alma | 2012-05-10 17:11:29 |
 Erre könnyű válaszolni, Gézoonak viszont csak később tudok a vizsgám miatt.
Természetesen mindkét koordinátarendszerből nézve a másik rendszer mérőrúdja megrövidül. Ugyanez érvényes az időkre is, ugyanolyan módon változnak. Teljesen szimmetrikus a két rendszer. Mondok egy analógiát.
Vegyél két közös origóval rendelkező euklideszi koordináta-rendszert, melyek egymáshoz képest el vannak forgatva! Mindkét rendszer x tengelyén vegyél fel egy L hosszúságú szakaszt. Ha a két szakaszt levetíted a másik koordináta-rendszer x tengelyére, mindkét esetben rövidülést tapasztalsz.
Na, specrelben ugyanez van, csak nem euklideszi, hanem minkowski térben. Az effektus lényege ugyanaz.
|
| Előzmény: [838] Zilberbach, 2012-05-10 16:41:42 |
|
| [838] Zilberbach | 2012-05-10 16:41:42 |
 Kezdek kissé összezavarodni.
Szeretnék szóbeli kérdést föltenni Almának és Gézoonak is:
Alább fölvázolok egy viszonylag egyszerű gondolatkísérletet - és annak néhány lehetséges kimenetelét, illetve az abból levonható következtetéseket. Kérem hogy válaszoljatok szerintetek melyik kimenetel, illetve következtetés az "igaz"?
Adott egy S és egy M jelű rendszer. Mindkét rendszerben ugyanazok az eszközök találhatók: egy nagyon pontos mérőrúd, úgy kialakítva, hogy a szomszédos rendszerből is jól és pontosan mérhető legyen (ezt nem is olyan egyszerű megoldani, ábra is tartozna hozzá de sajnos nem tudok ábrát rajzolni) és a szomszédos rendszer mérőrúdjainak hosszúságmérésére alkalmas eszközök. Kezdetben a két rendszer békésen pihen egymás mellett, és a rendszerekben tarózkodó fizikusok megelégedve tapasztalják, hogy mind a saját, mind a szomszédos rendszerekben lévő mérőrudak hossza pontosan 1 méter. Ezután az M rendszer gyors mozgásba kezd, és relativisztikus sebességet ér el (legyen mondjuk: 0,8 c). Ezzel a nagy sebességgel húz el a nyugalomban maradt S rendszer mellett - olyan közelségben, hogy mindketten újra megmérhessék a szomszédos rendszer mérőrúdjának hosszát.
A (fontosabb) lehetséges kimenetelek:
1.) Mindkét rendszerben az Einstein képletei által jósolt rövidüléseket mérik a másik rendszer mérőrúdjain.
Lehetséges logikai következtetés(ek):
A.) a rövdüléseket a sebességkülönbség okozta mérési zavar okozza, és nem a Lorentz-kontrakció - ami ezek szerint valójában nincs is. Az 1. lehetőség bekövetkezéseskor ez a valószínűleg helyes magyarázat. Mindkét rendszer egyenértékű a hosszúság kontrakció szempontjából (is?). (Az egyenértékűség nem is olyan nyilvánvaló, ugyanis az idő lassulása szempontjából a két rendszer nem egyenértékű: az idő lassulása ugyanis csak a gyorsított M rendszerben következik be, és csak az A rendszerből nézve, az M rendszerből nézve viszont az A rendszerben fölgyorsul az idő folyása.)
B.) az M rendszerben gyorsítása miatt valóban történt hosszkontrakció, de emellett még olyan mérési zavarok is kialakulnak, amik azt okozzák, hogy M-ből is - pont ugyanolyan mértékben - rövidebbnek mérik A-rendszer méterrúdját, és a mérési zavarok olyan jellegűek, hogy a megrövidült mozgó méterrúdjukkal is rövidültnek mérik az M rendszer méter-rúdját. Hát ezt nehéz józan ésszel elképzelni, hogy tényleg így legyen, de elvileg ez a lehetőség is fönnáll, ekkor a két rendszer több szempontból sem egyenértékű, nem szimmetrikus a mérési torzulásokra.
2.) Mindkét rendszerben pontosan 1m hosszúnak mérik a másik rendszer méter-rúdjait (is).
Lehetséges logikai következtetés(ek):
A.) nincs hosszkontrakció, nincsenek sebbesség okozta mérési zavarok. Ez igencsak valószínűtlen és erősen ellentmondana Einstein megállapításainak.
B.) az M rendszerben gyorsítása miatt történt hosszkontrakció, de emellett még olyan mérési zavarok is kialakulnak, amik ezt pontosan kompenzálják - nem valószínű, hogy így lenne.
3.) S-rendszerből rövidültnek mérik M-rendszer méter-rúdját viszont M-rendszerből hosszabbnak mérik S-rendszer méter-rúdját.
Lehetséges logikai következtetés: A Lorentz-kontrakció valóban, "fizikailag" lezajlik, mérés okozta torzulások viszont nincsenek.
Tovább is van (lenne) mondjam még? Nem ragozom tovább. A válaszokat előre is köszönöm.
|
|
| [837] Gézoo | 2012-05-10 05:45:06 |
 Kedves Alma!
"Kíváncsi lennék, hogy az s/t mennyiséget hogy értelmeznéd egy olyan mozgó koordinátarendszerben, melyben a járda és az eredetileg mozgást végző test is mozgást végez. "
Nagyon érdekes felvetés!
Áll a bakter a sín mellett és nézi, ahogy az elhaladó vonaton sétáló ember ruháján mászik egy szentjánosbogár.
És arra kíváncsi, hogy a vonat rendszeréből, hogyan látszik a szentjánosbogár.
Ami arra világít rá, hogy hogyan jelöljük a specrelben az egyes inercia rendszereket és a hozzájuk tartozó mérési értékeket.
Szuper! Nyilván tanultad, hogy a szentjánosbogárnak saját sebessége van abban a rendszerben ahol a bakter nyugszik. Saját sebessége van a vonat rendszerében és az emberhez rögzített rendszerben is.
Tehát adva van négy rendszer ebből három rendszer mozog a bakterhez képest.
A négy rendszer mindegyikéből a másik három rendszer 6-6 azaz összesen 24-féle képpen sorba rendezhető.
Azaz négy rendszer lehet aposztróf nélküli jelöléssel, és mindegyikhez 6-6 variációban ', '', és ''' aposztróf rendelhető a' szerint, hogy melyikből nézzük a többieket, illetve melyik a következő a láncban.
Így, a láncba fűzött rendszereknek az egymáshoz viszonyított sebességei attól függenek, hogy a 24 variáció melyikét alkalmazzuk. (Természetesen még több láncolt rendszer esetében a variációk száma sokszorozódik.)
Ugyanis más lesz a bogár és az ember közötti relatív sebesség a vonat, más a bakter és más a bogár vagy az ember rendszeréből mérve.
Tehát az így alkalmazott aposztróf indexek esetében valóban nem invariáns sem a sebesség, sem a Z, sem a 
Remélem belátod, hogy igazából a kezdeti ellenkezésednek nem az lett volna az alapja, hogy nem azzal a formulával számoljuk a hosszkontrakciót vagy az idődilatációt, hanem az alkalmazott aposztrófos jelölés mást jelent.
És így valóban nem invariáns egyetlen paraméter érték sem.
Ez viszont felveti egy másik problémát.
Ugyanis a mindenkori v sebességet v=c/n alakban megadva, az n állandósága mellett v csak úgy lehet változó értékű, ha c is változó értékű. Ez is és a  =c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának. =c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának.
Másik oldal viszont az, hogy a felsorolt invariancia lehetőségek mindegyike valóban invariáns közvetlen páronként, azaz
K-K1', K-K2', K-K3', .. , K-Kn' esetén.
|
| Előzmény: [836] Alma, 2012-05-09 23:03:54 |
|
| [836] Alma | 2012-05-09 23:03:54 |
 Ha jól értem a szép hosszú hozzászólásodban azt írtad le, hogy álló forrás által keltett sugárzás (transzformált) hullámhosszát megmérve mozgó koordinátarendszerben (ismervén a rendszer sebességét is), meghatározható a forrás nyugalmi rendszerbeli frekvenciája (ez egyébként nem is igaz, mert ismerni kell a sugárzás terjedési irányát is, de most nem akarok a 3D-vel kötekedni)
Te az invariáns szót kicsit furcsán használod egyébként. Akkor nevezünk (Lorentz) invariánsnak valamit, ha a (Lorentz) transzformáció invariánsan hagyja. Ehhez semmiféle átdefiniálgatásra nincs szükség, nem kell c° és egyéb kompenzáló mennyiségeket bevezetni.
Kíváncsi lennék, hogy az s/t mennyiséget hogy értelmeznéd egy olyan mozgó koordinátarendszerben, melyben a járda és az eredetileg mozgást végző test is mozgást végez.
Vagyis, definiáld kérlek az s'' és t'' mennyiségeket egy u sebességgel mozgó rendszerben úgy, hogy s'' / t''= s/t fennálljon!
|
| Előzmény: [835] Gézoo, 2012-05-09 15:40:51 |
|
| [835] Gézoo | 2012-05-09 15:40:51 |
 Kedves Alma!
"Testnek neveztem azt, ami a te rendszeredben mozog. "
Ami a járda rendszerében azzal a v sebességgel mozog, amely v sebesség van a két rendszer koordináta rendszereinek origói között, az a test a te rendszeredben nyugvó (álló), a sebessége nulla. Nyilván a járda mint test mozog a te rendszeredben, így a járda v sebességéről és a te rendszered valamely pontján való járda hossz (s'=s*ß) áthaladásának t' idejéről beszélhetünk áthaladási időként, és nem a te rendszeredben nyugvó test áthaladási idejéről, mert a nyugvónak nincs olyan ideje.
"A járdának van sebessége, meg is mondtam, hogy mennyinek gondolom, s'/t', ahogy te is."
Nagyon jó! Így van! Egyetértünk!
******* ******** ******** ******* ********
Ha jól látom, akkor alaposan körbejártuk ezt a témát. És bár, első ránézésre eretnek gondolatnak tűnt számodra a Z=s*t=s'*t' invariánskénti tálalása, a v sebesség "invarianciájának" egy fajta "szinonimájaként" felfogva, csak szokatlan, de éppen úgy invariáns.
A régi görög filozófusok felvetették azt a lehetőséget, hogy amikor kilövünk egy nyilat, akkor a nyíl, sok kis nyilacska sorozataként halad előrefelé.
Ilyen értelmezésben az időegységre eső útszakaszt a sebesség helyett az ismétlődési ütemmel, azaz a frekvenciával is jellemezhetjük.
Vagyis ha a hossz mércéje például egy adott frekvenciájú fényforrásból kilépő fény "f" frekvenciája, akkor a sebesség helyett ezzel is leírható lenne a hossz és az idő viszonya:
s=c°*t' alakban.
Nézzük azt is meg, hogy mit és miért jelöltem ezekkel a jelekkel:
Az f frekvenciájú fényt sugárzó fényforrás nyugodjon K rendszerben. Legyen egy v sebességgel mozgó K' rendszerben a megfigyelő aki így f' frekvenciának méri: f'=f*gyök((v+c)/(v-c)) függvény szerint (rel.Doppler) a fény frekvenciáját - közeledő 1D-s esetben -. Ha ez a K' rendszerben nyugvó megfigyelő képezi a "virtuális" c° sebességet: c°=c*gyök((v+c)/(v-c)) függvény segítségével, akkor az eredeti f frekvencia és Hertz függvényének - c=f* - felhasználásával az eredeti - felhasználásával az eredeti  hullámhossz: hullámhossz:  =c°/f' értéke megegyezik a forrás rendszerében lévő =c°/f' értéke megegyezik a forrás rendszerében lévő  =c/f hullámhossz értékével. =c/f hullámhossz értékével.
És miután az f' frekvenciára érvényes, hogy
f'=1/t'
így  =c°*t' alakkal a megmért t' periódusidővel és a "virtuális" c° fénysebességgel közvetlenül megkapjuk a forrás rendszerében mérhető =c°*t' alakkal a megmért t' periódusidővel és a "virtuális" c° fénysebességgel közvetlenül megkapjuk a forrás rendszerében mérhető  hullámhosszot. hullámhosszot.
Ha pedig ezt a  ; hullámhosszot a forrás rendszerében távolság, illetve hossz mérésre használtuk, akkor a K' rendszerben mért t' periódus idővel közvetlenül mérhetjük a forrás rendszerében lévő távolságokat. ; hullámhosszot a forrás rendszerében távolság, illetve hossz mérésre használtuk, akkor a K' rendszerben mért t' periódus idővel közvetlenül mérhetjük a forrás rendszerében lévő távolságokat.
Például t=1/3e8 [s] esetében a  =1 [m] és v=0,8c rendszerben ezzel c°=c*3 (v=0,8c esetében a gyök((v+c)/(v-c))=3 ) =1 [m] és v=0,8c rendszerben ezzel c°=c*3 (v=0,8c esetében a gyök((v+c)/(v-c))=3 )
Azaz a megmért t'=1/9e8 [s] periódusidővel a forrás rendszerben lévő hosszok:  =c°*t'=9e8/9e8= 1 [m] azaz a forrás rendszerében mérhető hullámhosszal azonos hossz. =c°*t'=9e8/9e8= 1 [m] azaz a forrás rendszerében mérhető hullámhosszal azonos hossz.
Miután minden v értékkel ugyanezt a  =1 [m] -t kapjuk a forrás rendszeri =1 [m] -t kapjuk a forrás rendszeri  =1 [m] hullámhossz esetében, elmondható, hogy a "virtuális" c° fénysebesség használatával a =1 [m] hullámhossz esetében, elmondható, hogy a "virtuális" c° fénysebesség használatával a  =c°*t'=v°*t' szintén invariáns. =c°*t'=v°*t' szintén invariáns.
Végezetül megemlítem, hogy ezek a gondolatok vélhetően éppen úgy szokatlanok a számodra mint az elsőként említett Z=s*t=s'*t' invariáns.
|
| Előzmény: [834] Alma, 2012-05-09 14:52:02 |
|



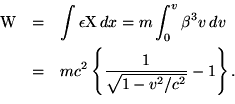
 szögű terjedés következtében.
szögű terjedés következtében. 
 =c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának.
=c/c'=1/gyök(1-(v/c)2) függvény is ellent mond a specrel-nek a fénysebesség állandóságáról kimondott posztulátumának.