| [1388] marcius8 | 2022-09-20 18:32:21 |
 Játékboltokban olykor van olyan kép, amit ha balról nézek, akkor ezt mutatja, ha jobbról nézek, azt mutatja. Ezt a jelenséget mutatja a színváltós rubik-kocka is, hogy a kis négyzetek attól függően, hogy honnan nézem őket, olyan színűek. (aki nem hiszi, hogy van színváltós rubik-kocka, írja be a keresőbe, és videón megnézheti.) Mi ennek a jelenségnek a neve, és hogyan működik az ilyen kép vagy színváltós papír, és hogy lehet ilyen színváltós papírt csinálni? Mindenki segítségét előre is köszönöm.
|
|
| [1387] Sinobi | 2022-04-01 16:35:46 |
 Fényforrás körüli egyenletes körmozgás esetén az érzékelt frekvenciát éppen az idődilatáció képletével kapod meg.
Hiszen ha T ideig áll fenn az állapot, akkor az érzékelt periódusok száma megegyezik a fényforrásnál és a megfigyelőnél, így csak az általuk érzékelt eltelt idő számít. (Ha akarjuk, akkor a megfigyelő és a fényforrásnál álló akár találkozhatnak is hogy információt cseréljenek, de ha T elég nagy, akkor az ehhez szükséges idő és a közben eltelő periódusok száma elhanyagolható az össz időhöz és periódusok számához képest.)
0.8 c-vel halad a megfigyelő (tök mindegy mekkora körpályán), a hozzá tartozó Lorentz faktor 1.666, így 400/0.6=666.66 TeraHertz frekvenciát érzékel a megfigyelő.
|
| Előzmény: [1386] marcius8, 2022-03-27 22:17:11 |
|
| [1386] marcius8 | 2022-03-27 22:17:11 |
 Mennyinek érzékeli vákuumban a megfigyelő a fényforrás által kisugárzott 400 TeraHertz frekvenciájú fény frekvenciáját, ha a megfigyelő a fényforrás körül egyenletes körmozgást végez 500 méter sugarú körpályán 240 ezer km/sec állandó nagyságú sebességgel? A vákuumbeli fénysebesség 300 ezer km/sec.
Mennyinek érzékeli vákuumban a megfigyelő a fényforrás által kisugárzott 400 TeraHertz frekvenciájú fény frekvenciáját, ha a fényforrás a megfigyelő körül egyenletes körmozgást végez 500 méter sugarú körpályán 240 ezer km/sec állandó nagyságú sebességgel? A vákuumbeli fénysebesség 300 ezer km/sec.
Előre is köszönöm mindenki segítségét, maradok tisztelettel: Bertalan Zoltán.
|
|
| [1385] Fálesz Mihály | 2022-02-12 11:41:16 |
 Az, hogy miért változik a képlet, világos: két különböző testből áll a rendszer, ezek nem ugyanúgy vannak felfüggesztve stb.
Az, hogy hogyan változik a képlet, sokkal összetettebb. Egy precíz megoldáshoz a rugóban haladó longitudinális hullámokat is figyelembe kell venni, tehát ki kell számolni a rendszer sajátfrekvenciáit. Nem egyetlen periódusidőről van szó, hanem végtelen sok féle periodikus rezgés szuperpozíciójáról.
***
Egy lehetséges első közelítő próbálkozás az, hogy a rugó tömegét pontszerű testtel helyettesítjük a nyújtatlan rugó felénél. Mondjuk a rugó tömege \(\displaystyle m\), a ráakasztott test tömege \(\displaystyle M\); a rugó két felének a megnyúlása \(\displaystyle f(t)\), illetve \(\displaystyle g(t)\), a fél rugók rugóállandója \(\displaystyle 2D\). A két test mozgását a következő egyenletek írják le:
\(\displaystyle m\cdot f'' = -2D\cdot (f-g); \qquad M\cdot (f+g)'' = -2D\cdot g. \)
Ha a sajátrezgést \(\displaystyle f(t)=A\sin(\omega(t-t_0))\), \(\displaystyle g(t)=B\sin(\omega(t-t_0))\) alakban keressük, akkor \(\displaystyle f''=-A\omega^2\sin(\omega(t-t_0))\) és \(\displaystyle g''=-B\omega^2\sin(\omega(t-t_0))\), ezért
\(\displaystyle mA\omega^2 =2D(A-B), \qquad M(A+B)\omega^2 = 2DB \)
Megoldva, kétféle körfrekvencia lehetséges:
\(\displaystyle \omega^2 = \frac{4D}{2M+m\pm\sqrt{4M^2+m^2}} . \)
(Félre: semmi garancia, hogy nem számoltam el, de azért megnyugtató, hogy \(\displaystyle m=0\) esetén \(\displaystyle \omega^2=\dfrac{D}{M}\), \(\displaystyle M=0\) esetén pedig \(\displaystyle \omega^2=\dfrac{2D}{m}\).)
Tehát a rendszer mozgása egy \(\displaystyle 2\pi\sqrt{\dfrac{2M+m+\sqrt{4M^2+m^2}}{4D}}\) és egy \(\displaystyle 2\pi\sqrt{\dfrac{2M+m-\sqrt{4M^2+m^2}}{4D}}\) periódusidejű rezgés összege.
|
| Előzmény: [1382] marcius8, 2022-02-10 20:24:48 |
|
|
|
| [1382] marcius8 | 2022-02-10 20:24:48 |
 Ismert, hogy a \(\displaystyle D\) rugóállandójú rugóhoz rögzített \(\displaystyle m\) tömegű test rezgésének periódusideje \(\displaystyle T=2\pi*\sqrt{\frac{m}{D}}\). Miért és hogyan módosul ez a képlet, ha a rugó tömegét is figyelembe vesszük? Előre is köszönöm mindenki segítségét.
|
|
| [1381] marcius8 | 2021-12-19 14:40:38 |
 Két, egymástól \(\displaystyle 3*10^{10}\) \(\displaystyle méter\) távol levő test tömege \(\displaystyle 9*10^{25} \) \(\displaystyle kg\) illetve \(\displaystyle 6*10^{25} \) \(\displaystyle kg\). Mekkora gravitációs erővel hat egymásra ez a két test?
A gravitációs állandó az egyszerűbb számolás miatt legyen \(\displaystyle \gamma=\frac{2}{3}*10^{-10}\) \(\displaystyle \frac{méter^3}{kg*sec^2}\).
Eddig még semmi extra nincs ebben a feladatban. De mi a válasz, ha 240000 km/sec sebességgel közeledünk/távolodunk a testekhez/testektől, a két testet összekötő egyenes mentén, illetve a két testet összekötő szakasz felezőmerőleges egyenese mentén, ekkor mi mennyinek látjuk a két test közötti gravitációs erőhatást?
|
|
| [1380] Lpont | 2021-07-19 09:02:48 |
 Fel lehetne éleszteni, pl. a lejárt határidejű KÖMAL feladatok topicban.
Az A jelű feladatok megoldásai csak nagyon ritkán kerülnek közlésre, sokunk tudását meghaladja azok nehézségi foka.
A fórumon viszont jó páran vagytok/voltatok - az előző évek, évtizedek alapján - , akiknek nem jelentenek nagy kihívást ezek a feladatok.
Egy-egy ötlet, vázlat, netán teljes megoldás közlése lendíthetne a fórumon.
|
| Előzmény: [1378] Zs76, 2021-06-21 20:09:29 |
|
|
| [1378] Zs76 | 2021-06-21 20:09:29 |
 Szerintem ennek a filmnek (Tenet) nem volt sok köze a tudományhoz, teljesen elvont fikciói volt, csak olyan elemeket tartalmazott, amik csak a filmvásznon történhetnek meg.
|
| Előzmény: [1376] PAL, 2020-08-31 01:41:55 |
|
| [1377] marcius8 | 2021-06-10 14:45:14 |
 Egy hídkapcsolás bal felső és jobb alsó eleme egy \(\displaystyle L\) induktivitású tekercs, jobb felső és bal alsó eleme egy \(\displaystyle C\) kapacitású kondenzátor, közélső eleme egy \(\displaystyle R\) ohmos ellenállás. Mekkora ennek a hídkapcsolásnak az eredő ellenállása? Ezen a hídkapcsolásnak egy \(\displaystyle U_0\) csúcsértékű \(\displaystyle omega\) frekvenciájú feszültség esik. Mekkora feszültség esik a tekercseken, a kondenzátorokon és az ellenálláson?
|
|
| [1376] PAL | 2020-08-31 01:41:55 |
 Üdv Mindenkinek!
Nem rég volt a TENET című film bemutatója, és engem az érdekelne, hogy egy fizikához értő egyén mennyit értett a film cselekményszálából, és az is érdekelne, hogy ennek a Nolan filmnek a látható történései mennyire hűek az ismert törvényekhez/elméletekhez, és mennyi benne a fikció? Esetleg laikusok számára megemlíthető a olyan könyv/példa amivel a film fizikája érthetőbb lesz. Az Interstellar esetében Kip Thorne Nobel-díjas fizikus "felügyelete" számomra egyfajta garancia volt a filmben előkerülő jelenségek valós bemutatására, hitelességére, ott 1-2 helyen már iskolás fejjel is megérthetők voltak a látottak/hallotak.
Köszönöm.
|
|
| [1375] marcius8 | 2020-08-01 17:09:16 |
 Nem régen olvastam, hogy a kínai Három Szurdok gát mögött annyi víz halmozódott fel, hogy az már mérhetően lassítja a Föld tengely körüli forgását. Ekkor ha csökken a Föld tengely körüli forgásának szögsebessége, csökken-e Föld forgásából származó forgási energia, és ha csökken ez az energia, mire fordítódik?
|
|
| [1374] marcius8 | 2020-08-01 17:06:38 |
 Azt tudjuk, hogy ahogy a Hold kering a Föld körül, a Hold Föld körüli keringése lassítja a Föld tengely körüli forgását, ennek oka a Holdnak a Földre kifejtett ár-apály erők. (A Hold gravitációs ereje a tengerek felszínét emeli illetve süllyeszti, és az így fellépő súrlódás például lassítja a Föld forgását.) Ugyanekkor a Hold egyre nagyobb sebességgel kering a Föld körül, és így a Hold a Földtől távolodik. De miért van az, hogy a Hold egyre nagyobb sebességgel kering a Föld körül?
|
|
| [1373] Berko Erzsebet | 2020-03-24 07:00:24 |
 Ott a hiba, hogy a gravitációs erő az csak a klasszikus fizikában használatos fogalom, és a klasszikus fizika csupáncsak bizonyos körülmények között használható közelítés. Pl. pici méreteknél a klasszikus fizika nem használható, hanem helyette a kvantummechanikát kell alkalmazni; nagy méretek és nagy gravitációs gyorsulások esetén pedig az általános relativitáselméletet kell alkalmazni, miként pl. a Te általad felvetett problémában is. Az általános relativitáselméletben nincs gravitációs erő, hanem görbült téridő van.
|
| Előzmény: [1372] marcius8, 2020-03-23 22:09:57 |
|
| [1372] marcius8 | 2020-03-23 22:09:57 |
 Tegyük fel, hogy egy bolygón a gravitációs térerősség \(\displaystyle g=0,5∗10^{14}\) \(\displaystyle \frac{méter}{sec^2}\). És tegyük fel, hogy ezen a bolygón \(\displaystyle h=900\) \(\displaystyle méter\) magasról álló helyzetből leesik egy test. Hol a hiba a következő gondolatmenetben? Én nem találtam meg.
Newton második törvénye miatt \(\displaystyle F=m*a\), ahol \(\displaystyle F\) a testre ható erő, \(\displaystyle m\) a test tömege, \(\displaystyle a\) a test gyorsulása. Legyen \(\displaystyle m_0\) a test nyugalmi tömege, azaz a test tömege akkor, amikor álló helyzetből el kezd esni. Ahogy esik a test, úgy a sebességének függvényében növekszik a test \(\displaystyle m\) tömege, és úgy növekszik a testet gyorsító gravitációs \(\displaystyle F=m∗g\) gravitációs erő, amely a testet gyorsítja. (Ugye, a testre ható gravitációs erő egyenlő a test tömegének és a gravitációs térerősségnek a szorzatával.) Alkalmazva az \(\displaystyle F=m∗a\) Newton-törvényt, ahol tehát \(\displaystyle F=m∗g\), adódik, hogy \(\displaystyle a=g\), azaz a test gyorsulása az esés alatt végig \(\displaystyle g=0,5∗10^{14}\) \(\displaystyle \frac{méter}{sec^2}\). Mivel a test a gyorsulása végig ennyi, és a test \(\displaystyle h=900\) \(\displaystyle méter\) magasról esik álló helyzetből, így a test sebessége \(\displaystyle v=\sqrt{2gh}\) sebességgel ér földet, ami éppen a fénysebesség.
|
|
|
|
| [1369] marcius8 | 2020-02-20 19:48:38 |
 Arra gondoltam, hogy a következő feladatot javaslom a fizika pontversenybe. De aztán mégsem javasoltam, mert egyrészt ebben a feladat inkább matekos jellegű, másrészt azért mert még én sem találtam meg a megoldást. Bármilyen segítséget előre is köszönök.
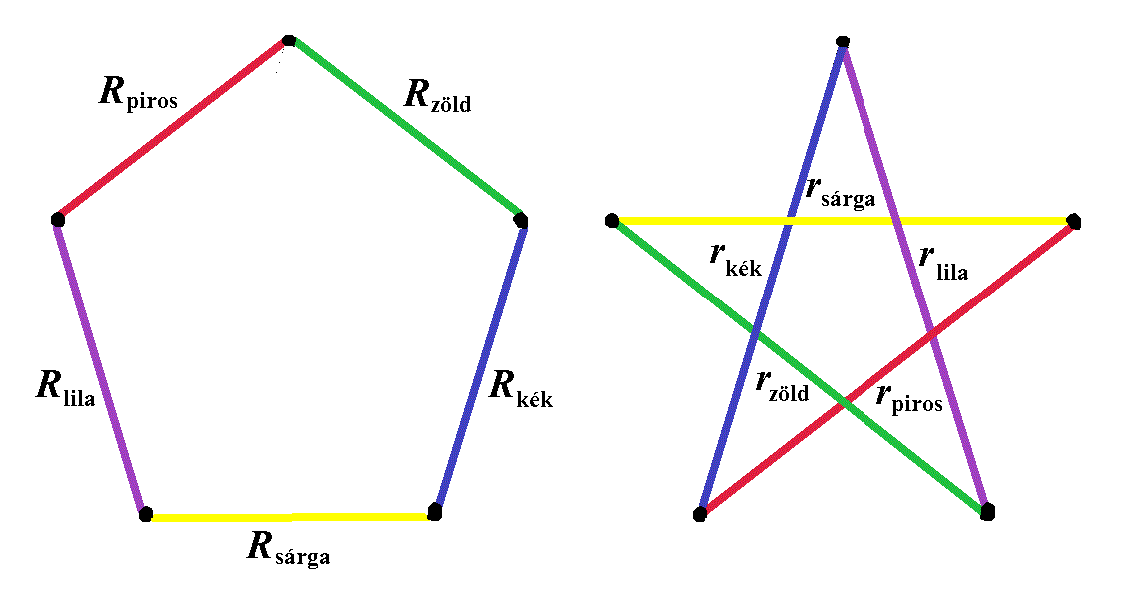
Egy szabályos ötszög csúcsait az oldalak mentén az ábrán látható módon összekötjük az \(\displaystyle R_{piros}\), \(\displaystyle R_{sárga}\), \(\displaystyle R_{zöld}\), \(\displaystyle R_{kék}\), \(\displaystyle R_{lila}\) ellenállás-huzalokkal. Ugyanennek a szabályos ötszögnek a csúcsait az átlók mentén összekötjük az \(\displaystyle r_{piros}\), \(\displaystyle r_{sárga}\), \(\displaystyle r_{zöld}\), \(\displaystyle r_{kék}\), \(\displaystyle r_{lila}\) ellenállás-huzalokkal.
Meghatározandóak az \(\displaystyle r_{piros}\), \(\displaystyle r_{sárga}\), \(\displaystyle r_{zöld}\), \(\displaystyle r_{kék}\), \(\displaystyle r_{lila}\) ellenállások, ha ismertek az \(\displaystyle R_{piros}\), \(\displaystyle R_{sárga}\), \(\displaystyle R_{zöld}\), \(\displaystyle R_{kék}\), \(\displaystyle R_{lila}\) ellenállások, és ha azt akarjuk, hogy az ötszög bármely két szomszédos csúcspontja között az eredő ellenállás változatlan maradjon.
Meghatározandóak az \(\displaystyle R_{piros}\), \(\displaystyle R_{sárga}\), \(\displaystyle R_{zöld}\), \(\displaystyle R_{kék}\), \(\displaystyle R_{lila}\) ellenállások, ha ismertek az \(\displaystyle r_{piros}\), \(\displaystyle r_{sárga}\), \(\displaystyle r_{zöld}\), \(\displaystyle r_{kék}\), \(\displaystyle r_{lila}\) ellenállások, és ha azt akarjuk, hogy az ötszög bármely két szomszédos csúcspontja között az eredő ellenállás változatlan maradjon.
|
 |
|
| [1368] Sinobi | 2019-12-27 10:42:51 |
 > „Napkelte esetén napforduló előtt, napnyugta esetén a napforduló után. QED.”
Mármint pont fordítva.
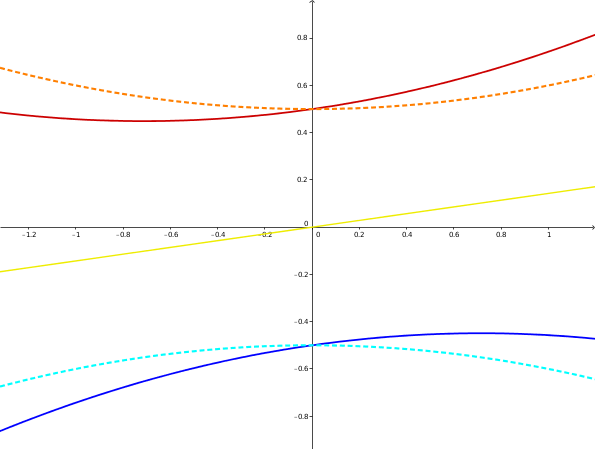
Sematikus ábra: vízszintesen a napok, függőlegesen az időpontok. A sárga a delelés időpontjának változása, a szaggatott ívek a napforduló környékén a deleléshez viszonyított időpontok, a folytonos ívek az "igazi", óra szerinti időpontok. A szélsőértékek balra illetve jobbra tolódnak.
|
 |
| Előzmény: [1367] Sinobi, 2019-12-26 12:35:18 |
|
| [1367] Sinobi | 2019-12-26 12:35:18 |
 Téli napfordulókor a Föld közelebb van a Naphoz mint átlagban, a szögsebessége nagyobb, két delelés között eltelő idő nagyobb, mint az átlagos 24 óra. Az eltérés megközelíti alulról a +- fél percet https://en.wikipedia.org/wiki/Solar_time#Apparent_solar_time.
Ezért napkelte és a napnyugta időpontjának a szélsőértéke ott lesz, amikor már +- 1 perccel csökken/növekszik a nap hossza (lásd ábra). Napkelte esetén napforduló előtt, napnyugta esetén a napforduló után. QED.
Adatok még pl itt találhatók: https://www.timeanddate.com/sun/hungary/budapest
(Tehát az jött ki, hogy ha mondjuk a napéjegyenlőségek éppen az ellipszis csúcsaiba esnének, akkor is elcsúszna a napkelte és a napnyugta időpontjának a szélsőértéke egymástól – nem tudom, hogy ez jó-e?)
Feladat: írjuk le a déli féltekén a napnyugta és a napkelte időpontjának a viselkedését.
Nézzük meg a nyári napforduló körüli időpontokat is!
Adjunk minél több adatra nagyságrendi becslést, és használjunk minél kevesebb kikeresett adatot!
|
| Előzmény: [1364] marcius8, 2019-12-12 09:07:13 |
|
|
|
| [1364] marcius8 | 2019-12-12 09:07:13 |
 Most tél van, és ilyenkor a Földön az északi féltekén rövidek a nappalok, és hosszúak az éjszakák. Valamikor karácsony környékén a legrövidebb a nappal, és a leghosszabb az éjszaka. Ebben még semmi különös sincsen. De! A Nap legkorábban valamikor december 14-e környékén nyugszik le a legkorábban, és valamikor január 4-e környékén kel fel a legkésőbb. Vajon a napkelte legkésőbbi időpontja és a napnyugta legkorábbi időpontja miért nincsen szinkronban egymással?
|
|










