Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] [212] [213] [214] [215] [216] [217] [218] [219] [220] [221] [222] [223] [224] [225] [226] [227] [228] [229] [230] [231] [232] [233] [234] [235] [236] [237] [238] [239] [240] [241] [242] [243] [244] [245] [246] [247] [248] [249] [250] [251] [252] [253] [254] [255] [256] [257] [258] [259] [260] [261] [262] [263] [264] [265] [266] [267] [268] [269] [270] [271] [272] [273] [274] [275] [276] [277] [278] [279] [280] [281] [282] [283] [284] [285] [286] [287] [288] [289] [290] [291] [292] [293] [294] [295] [296] [297] [298] [299] [300] [301] [302] [303] [304] [305] [306] [307] [308] [309] [310] [311] [312] [313] [314] [315] [316] [317] [318] [319] [320] [321] [322] [323] [324] [325] [326] [327] [328] [329] [330] [331] [332] [333] [334] [335] [336] [337] [338] [339] [340] [341] [342] [343] [344] [345] [346] [347] [348] [349] [350] [351] [352] [353] [354] [355] [356] [357] [358] [359] [360] [361] [362] [363] [364] [365] [366] [367] [368] [369] [370] [371] [372] [373] [374] [375] [376] [377] [378] [379] [380] [381] [382] [383] [384] [385] [386] [387] [388] [389] [390] [391] [392] [393] [394] [395] [396] [397] [398] [399] [400] [401] [402]

Szeretnél hozzászólni? Jelentkezz be.

[1697] magusocska

2007-01-08 08:03:44

Mellyek az a 9 jegyű számok, amire igazak az alábbiak:

a 9 jegyű szám osztható 9-el,

ha elhagyjuk az utolsó jegyét, akkor az így kapott 8 jegyű szám osztható 8-al,

ha elhagyjuk az utolsó jegyét, akkor az így kapott 7 jegyű szám osztható 7-el,

. . .

ha elhagyjuk az utolsó jegyét, akkor az így kapott 2 jegyű szám osztható 2-el.

Elég könnyű legalább egyet találni (pl. 13694729) a jegyenkénti szabályalkalmazással, de az összes megtalálására a brutal force-n kívül van -e módszer?

[1696] Lóczi Lajos	2007-01-07 14:29:20
Köszönöm, ezzel a kiegészítéssel már én is látom minden alesetben, hogy hogy mehet a sorozat -- szép gondolatmenet.
Előzmény: [1695] Sirpi, 2007-01-07 07:11:10

[1695] Sirpi

2007-01-07 07:11:10

Igaz, hogy már elhangzott egy sokkal frappánsabb megoldás (grat érte), de azért ha már kérdés, válaszolok:

Mivel |b_n/2-b_n+1|< $\varepsilon$ minden n>N-re a folytonosság miatt, ezért b_n/2- $\varepsilon$ $\leq$ b_n+1 $\leq$ b_n/2+ $\varepsilon$ . Vagyis ha b_n $\geq$ 3 $\varepsilon$ , akkor (3/2-1) $\varepsilon$ $\leq$ b_n+1, tehát nem válthat előjelet (a bal oldali egyenlőtlenséget felhasználva), másrészt b_n+1 $\leq$ b_n/2+ $\varepsilon$ $\leq$ b_n/2+b_n/3 $\leq$ b_n, tehát a sorozat monoton is.

Azt hittem, hogy ezek teljesen nyilvánvalónak látszanak az egyenlőtlenségből, azért nem részleteztem a dolgot ennyire.

Ha b_n<0, akkor ugyanez elmondható, csak akkor a sorozat alulról, szintén monoton módon megy be a [-3 $\varepsilon$ ;3 $\varepsilon$ ] intervallumba.

Előzmény: [1693] Lóczi Lajos, 2007-01-07 02:55:59

[1694] Lóczi Lajos

2007-01-07 03:23:19

Köszönöm a megoldásokat, az állítás igazsága viszont azt jelenti, hogy most van egy sokkal kevesebb számolást igénylő megoldásunk az [1681]-es hozzászólás feladatára, az ugyanis alig igényel számolást belátni, hogy

u_n=2n-4/3+a_n

alakú, ahol a_n+2a_n+1 nullához tart és korlátos, tehát most már valóban tudjuk, hogy maga a_n is nullához tart, ez pedig elég ahhoz, hogy a -19/12-et kihozzuk.

Előzmény: [1692] nadorp, 2007-01-07 00:32:48

[1693] Lóczi Lajos

2007-01-07 02:55:59

Nyilván azzal kell kezdeni a bizonyítást, hogy a b sorozat bemegy a [-3 $\varepsilon$ ,3 $\varepsilon$ ] intervallumba.

"Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 $\varepsilon$ felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2-nál nagyobb értékhez nem tud konvergálni."

De ha nem menne be, miért maradna 3 $\varepsilon$ felett? Miért ne ugrálhatna (pozitív és negatív értékekre) és főleg, miért kellene, hogy monoton legyen a b sorozat?

Előzmény: [1688] Sirpi, 2007-01-04 23:47:54

[1692] nadorp

2007-01-07 00:32:48

Bocs, elírtam a becslés második tagját, helyesen:

$\frac{N}{2^{n-N+1}}K$

Előzmény: [1691] nadorp, 2007-01-06 12:56:32

[1691] nadorp

2007-01-06 12:56:32

Legyen b_n=a_n+2a_n+1. Ekkor

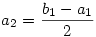
$a_2=\frac{b_1-a_1}2$

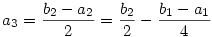
$a_3=\frac{b_2-a_2}2=\frac{b_2}2-\frac{b_1-a_1}4$

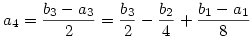
$a_4=\frac{b_3-a_3}2=\frac{b_3}2-\frac{b_2}4+\frac{b_1-a_1}8$

...

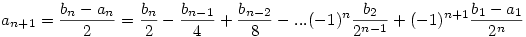$a_{n+1}=\frac{b_n-a_n}2=\frac{b_n}2-\frac{b_{n-1}}4+\frac{b_{n-2}}8-...(-1)^n\frac{b_2}{2^{n-1}}+(-1)^{n+1}\frac{b_1-a_1}{2^n}$ .

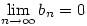Mivel $\lim_{n\to\infty}b_n=0$ , ezért n>N esetén |b_n|< $\epsilon$ , azaz

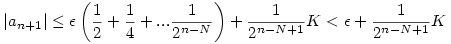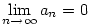
$|a_{n+1}|\leq\epsilon\left(\frac12+\frac14+...\frac1{2^{n-N}}\right)+\frac1{2^{n-N+1}}K<\epsilon+\frac1{2^{n-N+1}}K$ , ahol K a |b₁-a₁|,|b₂|,|b₃|... egy közös felső korlátja. ( Ez létezik, mert b_n konvergens). Innen már látszik, hogy $\lim_{n\to\infty}a_n=0$

Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16

[1690] Sirpi

2007-01-06 01:17:04

Nem feltételezek ilyet. Mindössze annyit, hogy van egy b_m $\neq$ 0, ahol m>N, ahol N az $\varepsilon$ -hoz tartozó korlát (azaz |b_n/2-b_n+1|< $\varepsilon$ minden n>N-re). Ekkor beláttam, hogy m-et növelve b_m előbb-utóbb bemegy a [-3 $\varepsilon$ ;3 $\varepsilon$ ] intervallumba (vagyis lehet bármilyen előjelű, megfelelően kis abszolútértékű szám), és utána viszont már nem megy ki belőle. Azaz minden $\varepsilon$ -ra van olyan N' index, hogy |b_n|< $\varepsilon$ minden n>N'-re. Tehát b_n $\to$ 0 és így a_n $\to$ 0.

Várom a következő kérdést :-).

Előzmény: [1689] Lóczi Lajos, 2007-01-06 00:20:29

[1689] Lóczi Lajos

2007-01-06 00:20:29

Sajnos nem értem a bizonyításod.

Számomra úgy tűnik, mintha azt feltételeznéd, hogy a b_n sorozat állandó előjelű már. Ha tévedek, akkor mondom a következő kérdésem :)

Előzmény: [1688] Sirpi, 2007-01-04 23:47:54

[1688] Sirpi

2007-01-04 23:47:54

Igaznak tűnik :-)

Tegyük fel, hogy a_n nem azonosan 0 egy adott indextől kezdve, és teljesül rá a feltétel. Cseréljük ki a_n-et egy b_n sorozatra úgy, hogy b_n=a_n, ha n páros, és b_n=-a_n, ha n páratlan. Ekkor a feltétel ekvivalens b_n/2-b_n+1 konvergenciájával (ezzel egyszerűbb talán dolgozni, mert nem "oszcillál").

Legyen $\varepsilon$ >0. Ekkor a konvergencia miatt van olyan N, hogy minden n>N-re |b_n/2-b_n+1|< $\varepsilon$ .

Mivel b_n nem azonosan nulla valamilyen indextől, ezért van olyan m>N, amire b_m $\neq$ 0 (feltehetjük, hogy pozitív, különben a b_n sorozat helyett vegyük az ellentettjét). Ekkor b_m/2- $\varepsilon$ $\leq$ b_m+1 $\leq$ b_m/2+ $\varepsilon$ , vagyis (és ez a lényeg) a sorozot b_m-től kezdve előbb-utóbb bemegy a [-3 $\varepsilon$ ;3 $\varepsilon$ ] intervallumba, és onnan már nem is tud kijönni, így 3 $\varepsilon$ -hoz van megfelelő N' korlát.

Az, hogy ha bemegy, akkor nem tud kijönni, triviális, hiszen 0/2- $\varepsilon$ $\leq$ b_n+1 $\leq$ 3/2 $\varepsilon$ + $\varepsilon$ , azaz a következő elem abszolútértéke 5/2 $\varepsilon$ lesz maximum. Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 $\varepsilon$ felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2 $\varepsilon$ -nál nagyobb értékhez nem tud konvergálni.

Tudom, ez így kicsit kusza, meg hosszú volt, de már kezd késő lenni. Nem tudom, van-e sokkal egyszerűbb(en leírható) megoldás.

Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16

Már regisztráltál?
Új vendég vagy?