| [1801] Lóczi Lajos | 2007-01-20 23:54:31 |
 A számítógép szépen végignézte az összes esetet, és persze megtalálta a (100,0,0,0,0,0), (50,50,50,50,0,0) optimumokat (és csak ezeket találta).
|
| Előzmény: [1799] HoA, 2007-01-20 19:43:10 |
|
| [1800] Lóczi Lajos | 2007-01-20 21:32:49 |
 Ó, persze, a nemnegativitási feltételeket kihagytam. Köszönöm, hogy rámutattál.
(Az zavarhatott meg, hogy egyenlőtlenséggel megadott feltételek esetén a multiplikátoroknak maguknak is nemnegatívnak kell lenniük, de ez még nem mond semmit a változókról...)
|
| Előzmény: [1799] HoA, 2007-01-20 19:43:10 |
|
| [1799] HoA | 2007-01-20 19:43:10 |
 A megfigyelt jelenség már akkor is előjön, ha csak az első feltételt vesszük. Legyen tehát
L(x,y, ):=x2+y2+ ):=x2+y2+ (100-x-y) (100-x-y)
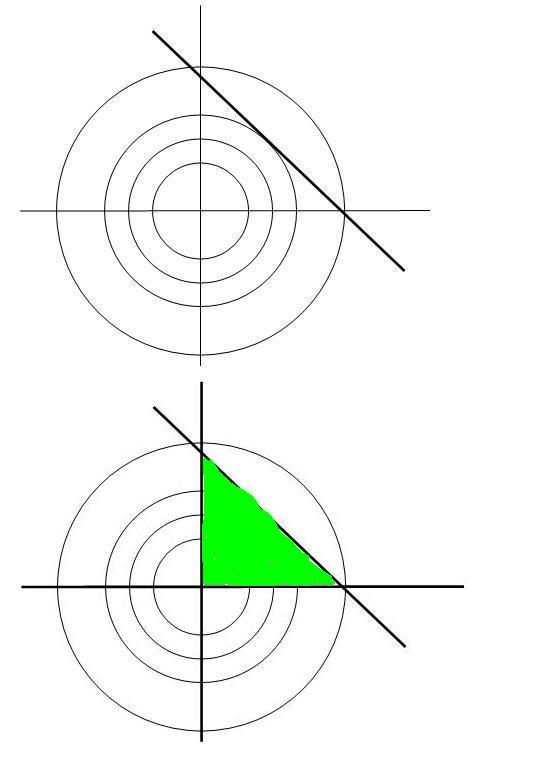
Az első két parciális deriváltból itt is kijön x=y. Ábrázoljuk az f(x,y)=x2+y2 függvényt az xy síkban szintvonalakkal: ezek nyilván origó középppontú koncentrikus körök. A vizsgált tartomány az x+y=100 egyenes által határolt félsík. f(x,y) a tartományban és a határán is tetszőleges nagy értéket felvehet, maximuma nincs. Az egyenes x=0 vagy y=0 értékkel jellemzett pontja, amelyekből az y=100 ill. x=100 érték adódna, semmilyen különleges szerepet nem játszik. Nem is csoda, hiszen nemcsak x és y nagyságviszonyát, hanem az x 0 , y 0 , y 0 feltételeket sem vettük figyelembe. Ha megtesszük, a Lagrange függvény így alakul: 0 feltételeket sem vettük figyelembe. Ha megtesszük, a Lagrange függvény így alakul:
L(x,y, 1, 1, 2, 2, 3):=x2+y2+ 3):=x2+y2+ 1(100-x-y)+ 1(100-x-y)+ 2(x-0)+ 2(x-0)+ 3(y-0) 3(y-0)
A megoldandó egyenletrendszerben a 0-t adó szorzatoknál 0 tényezőül {100-x-y=0; 2=0;y=0} -t választva x = 100, {100-x-y=0;x=0; 2=0;y=0} -t választva x = 100, {100-x-y=0;x=0; 3=0} -ból y = 100 adódik. A { 3=0} -ból y = 100 adódik. A { 1=0;x=0;y=0} választás a megengedett 1=0;x=0;y=0} választás a megengedett  alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y 100 és z+t+u+w 100 és z+t+u+w 100 mellett a w 100 mellett a w 0 , u 0 , u w , t w , t u, ... , x u, ... , x y feltételeket is figyelembe kell venni. Ezzel egyúttal a változók nemnegatív voltát is biztosítjuk. A 8 db 0 szorzat 0 tényezőinek megválasztásánál - 28 eset - anélkül, hogy mind a 256 kombinációt végignéznénk, csak rámutatunk, hogy a { w=0; u=w ; t=u; z=t ; y =z ; x+y = 100 } választás adja az x=100,y=z=t=u=w=0 megoldást, míg a { w=0; u=w ; z=t ; y =z ; x+y = 100 ; z+t+u+w = 100 } kombináció az x=y=z=t=50,u=w=0 eredményt. y feltételeket is figyelembe kell venni. Ezzel egyúttal a változók nemnegatív voltát is biztosítjuk. A 8 db 0 szorzat 0 tényezőinek megválasztásánál - 28 eset - anélkül, hogy mind a 256 kombinációt végignéznénk, csak rámutatunk, hogy a { w=0; u=w ; t=u; z=t ; y =z ; x+y = 100 } választás adja az x=100,y=z=t=u=w=0 megoldást, míg a { w=0; u=w ; z=t ; y =z ; x+y = 100 ; z+t+u+w = 100 } kombináció az x=y=z=t=50,u=w=0 eredményt.
|
 |
| Előzmény: [1791] Lóczi Lajos, 2007-01-19 01:16:58 |
|
|
| [1797] HoA | 2007-01-19 23:04:07 |
 A módszer az alábbi általánosításig biztosan működik:
- a két csoportban szereplő számok darabszáma ( most 2, ill. 4 ) legyen k ill. m.
- a csoportok elemeinek összege ( most 100,100) ne legyen nagyobb, mint A ill. B
Tehát legyen k+m számunk, x1,...,xk+m , ahol
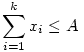 | (2) |
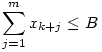 | (3) |
Mekkora 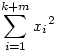 maximuma? maximuma?
Az összeget rögzített xk (az első csoport legkisebb eleme, az eddigi y) mellett vizsgáljuk. (1) -ből és (2) -ből 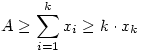 , , 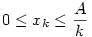 ( Ez egyben válasz Epsilon kérdésére: A=100 és k=2 esetére 0 ( Ez egyben válasz Epsilon kérdésére: A=100 és k=2 esetére 0 x2=y x2=y 50 ) Az [1795]-beli indokláshoz hasonlóan belátható, hogy az első csoport négyzetösszege akkor a legnagyobb, ha x2=x3=...=xk x1=A-(k-1).xk Példa: ha k=4,x4=4,A=22 , akkor { 10;4;4;4 } négyzetösszege nagyobb, mint pl. { 7;6;5;4 } -é. A második csoportra igaz az [1795]-beli szabály: ameddig lehet xk+j=xk egy szám pedig B és az eddigiek összegének különbsége: xk+1=xk+2=...=xk+d=xk,xk+d+1=B-d.xk Az [1795]-beli szakaszhatárok most a 50 ) Az [1795]-beli indokláshoz hasonlóan belátható, hogy az első csoport négyzetösszege akkor a legnagyobb, ha x2=x3=...=xk x1=A-(k-1).xk Példa: ha k=4,x4=4,A=22 , akkor { 10;4;4;4 } négyzetösszege nagyobb, mint pl. { 7;6;5;4 } -é. A második csoportra igaz az [1795]-beli szabály: ameddig lehet xk+j=xk egy szám pedig B és az eddigiek összegének különbsége: xk+1=xk+2=...=xk+d=xk,xk+d+1=B-d.xk Az [1795]-beli szakaszhatárok most a 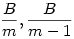 ... értékek. Vegyük észre, hogy ... értékek. Vegyük észre, hogy 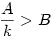 esetén xk>B is előfordulhat, tehát maga B is lehet szakaszhatár. Ekkor a második csoport első eleme B, a többi 0. Másrészt ha esetén xk>B is előfordulhat, tehát maga B is lehet szakaszhatár. Ekkor a második csoport első eleme B, a többi 0. Másrészt ha 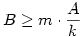 akkor a második csoportba mindig "belefér" m darab xk érték, tehát görbénk csak egyetlen parabolaívből áll. Függvénygörbénk - a maximális négyzetösszeg xk tól függése - vizsgálatát másokra hagyom. akkor a második csoportba mindig "belefér" m darab xk érték, tehát görbénk csak egyetlen parabolaívből áll. Függvénygörbénk - a maximális négyzetösszeg xk tól függése - vizsgálatát másokra hagyom.
|
| Előzmény: [1796] epsilon, 2007-01-19 17:09:25 |
|
| [1796] epsilon | 2007-01-19 17:09:25 |
 Helló HoA! Valóban elemi, logikus, szép. Van néhány kérdöjelem, amit magamban kellene tisztáznom: Az y nem több mint 50 az indulásból feltehető? Továbbá ha általánosítani kellene, a 100 helyett pl. 2a lenne, na meg a tagok száma 6 helyett n, akkor az általad jelzett 3 intervallumba sorolás az y-ra vonatkozóan hogyan alakulna, mindegyiket külön-külön elemezni kellene, vagy belátható-e elég könnyen, hogy a sok lokális maximumból melyik is a globális maximum? Én ezeken tűnődöm, ha vannak megjegyzéseid, szívesen veszem, és kösz, a megoldásodban volt jó pár mentő ötlet! Üdv: epsilon
|
|
| [1795] HoA | 2007-01-19 11:20:58 |
 Egy elemi eszközöket használó megoldás lépései:
Bontsuk a négyzetösszeget két részre, legyen az első tag x2+y2 , a második z2+t2+u2+w2 . Vizsgáljuk a maximumot rögzített y mellett (0 y y 50). Az első tag nyilván akkor a legnagyobb, ha x = 100 - y. A második tagban keressük négy 0 és y közötti z,t,u,w szám maximális négyzetösszegét, ahol z+t+u+w<=100 . 50). Az első tag nyilván akkor a legnagyobb, ha x = 100 - y. A második tagban keressük négy 0 és y közötti z,t,u,w szám maximális négyzetösszegét, ahol z+t+u+w<=100 .
1) Belátható, hogy ha z+t+u+w<100 és nem mindegyik = y, akkor az y-nál kisebb számok növelésével a négyzetösszeg nő.
2) Belátható, hogy rögzített z+t+u+w mellett a négyzetösszeg nő, ha egy nagyobb számot növelünk és egy kisebbet csökkentünk: Szabatosan : Ha z>t d>0, akkor (z+d)2+(t-d)2>z2+t2 d>0, akkor (z+d)2+(t-d)2>z2+t2
1) -ből és 2) -ből következik, hogy a második tag akkor a legnagyobb, ha z,t,u,w ameddig csak lehet = y , egy szám pedig a többiek 100-ból vett maradéka. Vagyis a második tag szerkezete függ y-tól. Szabatosan: Ha 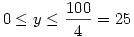 , akkor a második tag maximuma 4y2 , a két tag összege , akkor a második tag maximuma 4y2 , a két tag összege
. Ha 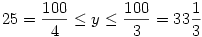 , akkor a második tag maximuma 3y2+(100-3y)2 , a két tag összege , akkor a második tag maximuma 3y2+(100-3y)2 , a két tag összege
| (100-y)2+4y2+(100-3y)2 | (2) |
. Végül ha 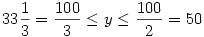 , akkor a második tag maximuma 2y2+(100-2y)2 , a két tag összege , akkor a második tag maximuma 2y2+(100-2y)2 , a két tag összege
| (100-y)2+3y2+(100-2y)2 | (3) |
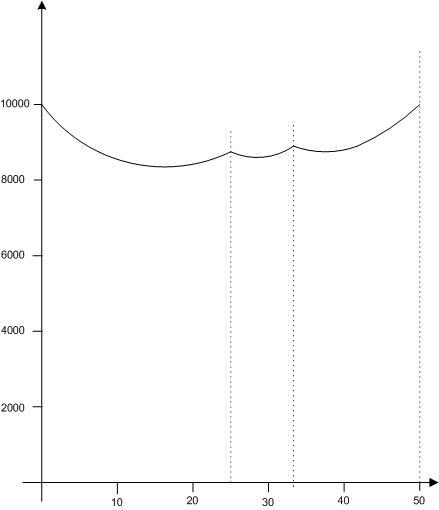
A négyzetösszeg maximumot y függvényében ábrázolva tehát egy három, egymáshoz csatlakozó, alulról konvex parabolaívből álló görbét kapunk. A teljes y tartományra a maximumot ezért csak a széleken és a csatlakozási pontokban kell vizsgálni. természetesen a már ismert eredményt kapjuk: A maximum 10000, amit az x=100, y=z=t=u=w=0 és az x=y=z=t=50, u=w=0 értékrendszerek adnak.
|
 |
| Előzmény: [1792] epsilon, 2007-01-19 07:16:56 |
|
| [1794] epsilon | 2007-01-19 11:16:20 |
 Szerintem nem, mert ennél nem használtuk fel a betűk közötti rendezési sorrendet, és ha annélkül kijönne, akkor...nem stimmel mert a feltételek nélkül más értékekre nagyobb lehet a maximum. Vagyis akár rendezett sorrenddel, akár annélkül, nem jöhet ki ugyanaz.
|
|
| [1793] Cckek | 2007-01-19 10:15:30 |
 Nos a kérdésem az, hogy ezen feltételek mellett fennáll-e a
(x+y+z+t+u+w)2+(x-y)2+(x-z)2+(x-t)2+(x-u)2+(x-w)2+(y-z)2+(y-t)+(y-u)2+(y-w)2+(z-t)2+(z-u)2+(z-w)2+(t-u)2+(t-w)2+(u-w)2 6.1002 egyenlőtlenség? Ugyanis ekkor a Lagrange azonosságból következik a maximum. 6.1002 egyenlőtlenség? Ugyanis ekkor a Lagrange azonosságból következik a maximum.
|
| Előzmény: [1791] Lóczi Lajos, 2007-01-19 01:16:58 |
|
| [1792] epsilon | 2007-01-19 07:16:56 |
 Egy biztos: a feladatot olyan helyen találtam, hogy elemi eszközökkel gondoltak a megoldására. Ahogy viccese mondják, ezt analízissel megoldani olyen mint a bolhavadászat fejszével :-) Az alapelgondolásom az volt (az y-nál kisebb rendett számok miatt), hogy mivel előtte csak 1 szám van, nála kisebb meg 4 szám, ezért az x maximizálása sokkal gyengébb mint az y maximizálása, ami által a többi 4 szám maximizálható, és ezeket maximizálva jobban közeledünk a négyzetösszeg maximumához. Valahogyan nem illik ebbe a képbe a 100, és a többi 0 megoldás. Persze mindez csak érzés, sejtés, de...???
|
|




 ):=x2+y2+
):=x2+y2+ 0 , y
0 , y alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y
alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y 100 és z+t+u+w
100 és z+t+u+w

 ,tg
,tg
 Q.
Q. 
