| [2453] Sirpi | 2007-11-26 12:53:02 |
 Felmerült bennem egy probléma, egyelőre csak ízlelgetem. Az egyszerűség kedvéért nevezzünk rácsidomnak rácsnégyzetekből álló, élek mentén illeszkedő, összefüggő alakzatokat (gondoljatok a tetrisre, de nem feltétlen kell 4 kis négyzetből állnia az alakzatnak). Ezek között vannak olyanok, amiket többször felhasználva ki lehet rakni egy téglalapot, másokból meg nem. Az előbbiekhez rendeljük hozzá az ehhez szükséges minimális darabszámot. Tehát ha az alakzat eleve téglalap, akkor 1-et, a tetrisben pedig pl. az L-alakhoz 2-t, a T-alakhoz 4-et rendelünk.
A kérdés az, hogy mekkora lehet maximálisan ez a szám? Vagy egyáltalán, milyen más értékek adódhatnak így?
Mindenesetre találtam 4-nél nagyobbat már, innen jött az ötlet.
|
|
| [2452] Lóczi Lajos | 2007-11-25 22:46:37 |
 Nem olyan nehéz ez.
Tudjuk, hogy x, y és z pozitívak. Az x g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B 0, A>0, B>0.
Azt kapjuk, hogy
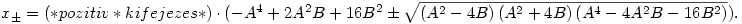
Ki akarjuk zárni, hogy g<0 pozitív x-ekre.
Ha a diszkrimináns negatív, készen vagyunk.
Ha a diszkrimináns A2-4B miatt nulla, szintén készen vagyunk, mert ez annak felel meg, ha y=z, de  .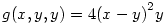
Elég tehát az A4-4A2B-16B20 esetben megvizsgálni, hogy a nagyobbik gyök, x+ lehet-e pozitív.
Elemi módon látszik, hogy A4-4A2B-16B20 és -A4+2A2B+16B20 és A2-4B0 egyszerre nem teljesülhetnek a pozitív számpárok körében.
Az kell tehát csak megnézni, mi van, ha -A4+2A2B+16B2 0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van.
|
| Előzmény: [2450] Lóczi Lajos, 2007-11-25 20:32:12 |
|
| [2451] Róbert Gida | 2007-11-25 20:51:55 |
 Igen, ezt kell belátni, nem szabadott volna négyzetre emelnem, mert a jobb oldal negatív is lehet, köszönhetően annak, hogy: igaz, hogy R2*r teljesül, de R bármekkora lehet rögzített r mellett.
Egyébként szabályos háromszögre egyenlőséggel, ez megfelel x=y=z-nek és g(x,x,x)=0
|
| Előzmény: [2450] Lóczi Lajos, 2007-11-25 20:32:12 |
|
|
|
| [2448] Róbert Gida | 2007-11-25 16:29:22 |
|
Hm, a polinom lexikografikusan legnagyobb tagjának negatív az együtthatója, ergó számtani-mértani egyenlőtlenségekkel ezt nem lehet belátni.
A polinom egyébként homogén hatodfokú, így feltehető például, hogy x=1 teljesül. (Kicsivel rövidebb lesz akkor a képlet.)
|
| Előzmény: [2446] Róbert Gida, 2007-11-25 16:14:49 |
|
|
| [2446] Róbert Gida | 2007-11-25 16:14:49 |
|
A következőkkel próbálkoztam:
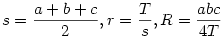
Majd egy háromszögekre való egyenlőtlenség bizonyításának ismert technikája: legyen
x=s-a,y=s-b,z=s-c
Ekkor x,y,z>0 teljesül, megfordítva minden pozitív x,y,z-re tartozik pontosan egy háromszög. (oldalaira a háromszög-egyenlőtlenség teljesül). Ezt beírva és négyzetre emelve és rendezve az oldalt kapjuk: f(x,y,z)=4yz(x+z)2(x+y)2-(16xyz-(x+y)(y+z)(z+x))2 kell teljesülnie minden pozitív x,y,z számokra. Ez a polinom viszont a maple szerint irreducibilis a racionális többváltozós test felett. Egy nehéz módszer ilyenkor, hogy számtani-mértani egyenlőtlenségek tucattyaival igazolni, hogy f(x,y,z) pozitív, de ennek a megtalálása egyáltalán nem triviális, illetve van amikor nem is lehetséges, annak ellenére, hogy az egyenlőtlenség igaz.
|
| Előzmény: [2443] Gyöngyő, 2007-11-25 13:26:07 |
|
|
|
