Fórum: Érdekes matekfeladatok

A céltábla középpontja csak a 2×2-es négyzet közepébe eső 1×1-es négyzetbe eshet. Egy lövés akkor találja el a céltáblát, ha annak sugarú környezetébe esik a céltábla középpontja. A kérdés tehát az, legkevesebb hány sugarú körrel fedhető le az egységnégyzet. Ehhez pedig legalább 4 szükséges ugyanis tekintsük a négyzet sarkait, ha 3 körrel le tudnánk fedni, lenne két sarok amit ugyanaz a kör fed le. Ez csak úgy lehet ha az egyik oldal a az egyik kör átmérője, a kimaradó rész pedig könnyen láthatóan nem fedhető le 2 körrel (a két már lefedett sarokhoz akármilyen közel van még lefedendő pont így megint oldal átmérőjű köröket kell elhelyezni).

4 elég.

Egy 2x2 méteres négyzet alakú papírlap mögött el van rejtve egy 1 méter átmérőjű kör alakú céltábla. Legalább hányszor kell rálőnie egy mindig pontosan célzó mesterlövésznek, hogy biztosan eltalálja a céltáblát? (A találatok pontszerűek, a céltábla pereme is érvényes találat.)

Nagyon szép. Máris találtunk 3 látszólag teljesen különböző rekurziót. Mepróbáltam a teljes indukciós bizonyítást, egyelőre nem sokra jutottam vele, de még nem adtam fel. Azért nem könnyű. Kiváncsi lennék egy közvetlen kombinatorikai gondolatmenetre, ami egyből kiadja a zárt alakot.

Legyen n db nyitó és n db záró zárójelünk. A helyes zárójelezések száma a_n.

a₀=1

Vizsgáljuk meg, hogy n+1 db nyitó és záró zárójelből hány zárójelezés készíthető. A zárójelezés nyilván egy nyitó zárójellel kezdődik, ennek keressük meg a záró párját. A kettő között elhelyezkedik k db zárójelpár, utána pedig n-k:

( k db zárójelpár ) n-k db zárójelpár

A két zárójel között a_k, utána pedig a_n-k zárójelezés készíthető. Mivel k 0-tól n-ig terjedhet, ezért:

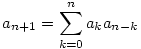
Sirpi Wikipédiás linkje alapján ezek egyértelműen a Catalan számok.

Egyébként ezt az angol nyelvű linket is érdemes megnézni, itt 3 különböző bizonyítás is van a dologra (egy generátorfüggvényes és két elemi - utóbbinak külön szépsége, hogy az szorzót is megmagyarázza), zárójelezés helyett jobbra és felfelé lépkedő, főátló alá nem lépő királlyal.

Szép gondolat a rossz zárójelezések összeszámolásának ez a formája. Köszönöm a segítséget!

A képlet helyesen:

A p_n,z-re (ha nz) nem tudok zárt képletet, de p_n,n másképp is felírható, ami alapján egy teljes indukciós bizonyítás sikerre kell hogy vezessen. Az összes zárójelezések száma 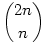, amiből ki fogjuk vonni a rossz zárójelezések számát. Vezessünk be egy s számlálót 0 kezdőértékkel, amely a zárójelekből álló sztringet elejétől olvasva 1-gyel nő, ha nyitó, illetve 1-gyel csökken, ha záró zárójelet olvasunk. A zárójelezés nyilván akkor romlik el, amikor az s -1 -et vesz fel, ez pedig csak páratlan pozícióban lehet. Pl. nyilván rossz a zárójelezés, ha )-lel kezdődik. Tehát a következőképpen számolunk: A szóban forgó páratlan pozíció (2i+1) előtt befejezett, jó zárójelezés áll (s=0), aztán záró zárójel következik. Ezen esetek száma az előző 2i pozíción létrejövő jó zárójelezések száma (p_i,i), szorozva a 2i+2 -edik pozíciótól kezdődő összes zárójelezések számával (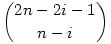). Ha i megy 0-tól n-1 -ig, ezek összege megadja az összes rossz zárójelezést. Vagyis:

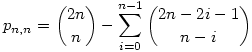
Ebben a rekurzióban már csak egy index szerepel, úgyhogy teljes indukcióval bebizonyítható, hogy a Catalan számokat adja. Sok sikert.

Szia Attila!

Kösz a segítséget! Én is a Catalan számokra gondoltam, csak még bizonyítani kéne.