| [2925] MTM | 2009-04-21 17:25:26 |
 501. feladat:
Adjunk meg végtelen sok pozitív egész c számot, amire
a, 7c2+1
b, 13c2+1
négyzetszám.
|
|
| [2924] HoA | 2009-04-21 12:10:19 |
 500. feladat Nevezzük egy pénztáros csoporthoz tartozó tiltott zárnak (TZ) az olyan zárat, amelyet a csoport tagjai együtt sem tudnak kinyitni. A feltételek értelmében minden egy és kételemű csoportnak van TZ-je, de a három vagy négyelemű csoportoknak nincs. Két kételemű csoportnak – párnak - nem lehet közös TZ-je, hiszen akkor a két pár egyesítéséből adódó legalább 3 elemű csoport nem tudná ezt a zárat kinyitni. Mivel 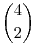 = 6 pár van, legalább 6 TZ kell legyen, és mivel éppen 6 zár van, minden párnak pontosan egy TZ-je van. Minden pénztáros 3 pár tagja, így nem lehet nála e három pár TZ –jének kulcsa, vagyis legfeljebb 6-3 = 3 kulcsa lehet. Másrészt 3 olyan pár van, amelyiknek egy kiválasztott pénztáros nem tagja. E 3 pár TZ-jének kulcsa nála kell legyen, különben az egyik ilyen párral hármas csoportot alkotva a pár TZ-jét nem tudnák kinyitni. Ezért legalább 3 kulcsa van. Tehát a feladat kikötése „melynél mindegyik pénztáros ugyanannyi kulccsal rendelkezik” elhagyható, csak ilyen elosztás lehetséges: mindenkinek 3 kulcsa van. A TZ-k párokhoz rendelése a kulcselosztást egyértelműen meghatározza: a fentiek szerint minden pénztáros azzal a 3 kulccsal rendelkezik, amelyik az őt nem tartalmazó párok TZ-jét nyitja. Így a kulcselosztások száma annyi, ahányféleképpen a 6 TZ hozzárendelhető a hat párhoz: 6! = 720. = 6 pár van, legalább 6 TZ kell legyen, és mivel éppen 6 zár van, minden párnak pontosan egy TZ-je van. Minden pénztáros 3 pár tagja, így nem lehet nála e három pár TZ –jének kulcsa, vagyis legfeljebb 6-3 = 3 kulcsa lehet. Másrészt 3 olyan pár van, amelyiknek egy kiválasztott pénztáros nem tagja. E 3 pár TZ-jének kulcsa nála kell legyen, különben az egyik ilyen párral hármas csoportot alkotva a pár TZ-jét nem tudnák kinyitni. Ezért legalább 3 kulcsa van. Tehát a feladat kikötése „melynél mindegyik pénztáros ugyanannyi kulccsal rendelkezik” elhagyható, csak ilyen elosztás lehetséges: mindenkinek 3 kulcsa van. A TZ-k párokhoz rendelése a kulcselosztást egyértelműen meghatározza: a fentiek szerint minden pénztáros azzal a 3 kulccsal rendelkezik, amelyik az őt nem tartalmazó párok TZ-jét nyitja. Így a kulcselosztások száma annyi, ahányféleképpen a 6 TZ hozzárendelhető a hat párhoz: 6! = 720.
|
| Előzmény: [2916] lorantfy, 2009-04-19 15:08:06 |
|
|
| [2922] jenei.attila | 2009-04-20 09:15:07 |
 Először én is a skatulya elvvel hasonló módon próbáltam bizonyítani mint te, mert intuitíve elég nyilvánvalónak tűnik, hogy az {nx} (x rögzített irracionális, n végigfut az egészeken) sűrű [0,1] intervallumban és nem maradnak rések. Egy kicsit tovább gondolva azért rendbe lehet tenni ezt a bizonyítást: osszuk a [0,1] intervallumot N egyenlő részre, ahol 1/N< . Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}< . Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}< , amiből {(i-j)x}< , amiből {(i-j)x}< következik (feltehető hogy i>j). Definíció szerint legyen h:={(i-j)x}. Mivel h< következik (feltehető hogy i>j). Definíció szerint legyen h:={(i-j)x}. Mivel h< , ezért [0,1] minden 1/N hosszúságú részintervallumában megtalálható lesz h-nak valamelyik többszöröse. Tehát tetszőlegesen kiválasztva egy részintervallumot, valamely k természetes számmal kh eleme lesz ennek a részintervallumnak. Azonban kh=k{(i-j)x}={k(i-j)x}, azaz ha m-et k(i-j) -nek definiáljuk, x-nek olyan mx többszörösét kapjuk, amelynek törtésze az előre kiválasztott 1/N hosszú részintervallumban van. Ez pedig már tényleg azt jelenti, hogy {nx} sűrű [0,1]-ben. Visszatérve az irracionális számok másodrendű racionális közelíthetőségére: úgy tűnik, hogy ez és a most skatulyaelvvel bizonyított állítás ekvivalensek. Tehát próbáljuk meg skatulyaelvvel bizonyítani, hogy tetszőleges x irracionális számra végtelen sok a,b természetes szám létezik, hogy , ezért [0,1] minden 1/N hosszúságú részintervallumában megtalálható lesz h-nak valamelyik többszöröse. Tehát tetszőlegesen kiválasztva egy részintervallumot, valamely k természetes számmal kh eleme lesz ennek a részintervallumnak. Azonban kh=k{(i-j)x}={k(i-j)x}, azaz ha m-et k(i-j) -nek definiáljuk, x-nek olyan mx többszörösét kapjuk, amelynek törtésze az előre kiválasztott 1/N hosszú részintervallumban van. Ez pedig már tényleg azt jelenti, hogy {nx} sűrű [0,1]-ben. Visszatérve az irracionális számok másodrendű racionális közelíthetőségére: úgy tűnik, hogy ez és a most skatulyaelvvel bizonyított állítás ekvivalensek. Tehát próbáljuk meg skatulyaelvvel bizonyítani, hogy tetszőleges x irracionális számra végtelen sok a,b természetes szám létezik, hogy 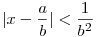
|
| Előzmény: [2920] jonas, 2009-04-19 16:08:39 |
|
| [2921] jenei.attila | 2009-04-19 17:14:21 |
 Sajnos még mindig nem értem. Amikor ezt írod "{floor(np)} sűrű a [0..1] intervallumon"; itt a floor mit jelent? Az alsó egészrész? Ez ugye nem kell. Az állítás szerintem: tetszőleges adott p irracionális számra az {np} alakú számokból álló halmaz (ahol n végig fut az egész számokon) sűrű [0,1]-ben. "Vegyük most a p első 1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ )p számokat. Ezek mindegyike 0 és 1 közé esik" ezt szintén nem értem. Ha pl )p számokat. Ezek mindegyike 0 és 1 közé esik" ezt szintén nem értem. Ha pl  , akkor p többszörösei nem esnek 0 és 1 közé. Itt valószínűleg a többszörösök törtrészére gondoltál. "Az np törtrész többszöröseiről nem azt mondom, hogy sűrűek, hanem csak azt, hogy legfeljebb , akkor p többszörösei nem esnek 0 és 1 közé. Itt valószínűleg a többszörösök törtrészére gondoltál. "Az np törtrész többszöröseiről nem azt mondom, hogy sűrűek, hanem csak azt, hogy legfeljebb  távolságra vannak egymástól". Itt szerintem az np többszörösök törtrészeire gondoltál. Azt nem értem, hogy ezekről mi alapján állítod, hogy "legfeljebb távolságra vannak egymástól". Itt szerintem az np többszörösök törtrészeire gondoltál. Azt nem értem, hogy ezekről mi alapján állítod, hogy "legfeljebb  távolságra vannak egymástól". Mert az OK, hogy van olyan távolságra vannak egymástól". Mert az OK, hogy van olyan  hosszú intervallum, amelybe p legalább két többszörösének törtrésze esik, de miből tudjuk, hogy nem marad ki valamely hosszú intervallum, amelybe p legalább két többszörösének törtrésze esik, de miből tudjuk, hogy nem marad ki valamely  hosszú intervallum? Nem akarlak megsérteni, de szerintem ez a bizonyításod így nem jó. Esetleg ha agy numerikus példán mutatnád be... hosszú intervallum? Nem akarlak megsérteni, de szerintem ez a bizonyításod így nem jó. Esetleg ha agy numerikus példán mutatnád be...
|
| Előzmény: [2920] jonas, 2009-04-19 16:08:39 |
|
| [2920] jonas | 2009-04-19 16:08:39 |
 A bizonyítást tényleg nem igazán jól írtam le.
Az np törtrész többszöröseiről nem azt mondom, hogy sűrűek, hanem csak azt, hogy legfeljebb  távolságra vannak egymástól, így bármilyen valós számhoz van legfeljebb távolságra vannak egymástól, így bármilyen valós számhoz van legfeljebb  /2 távolságra egy többszörös. Mivel azonban ez minden /2 távolságra egy többszörös. Mivel azonban ez minden  -ra igaz, ezért a p összes többszörösének törtrészei már sűrűek a [0..1]-ben. -ra igaz, ezért a p összes többszörösének törtrészei már sűrűek a [0..1]-ben.
Azt, hogy p irracionális, ott használtam föl, hogy a p többszöröseinek törtrészei nem esnek egybe, mert ellenkező esetben előfordulhatna, hogy a két egy intervallumba eső egészrész valójában egyenlő, vagyis floor(np)=0, amikor is a bizonyítás nem működik.
|
| Előzmény: [2918] jenei.attila, 2009-04-19 15:47:28 |
|
|
| [2918] jenei.attila | 2009-04-19 15:47:28 |
 Az igaz, hogy lesz olyan epszilon hosszú intervallum amelyikbe két többszörös kerül. De ez még nem biztosítja azt, hogy nem lesz olyan epszilon hosszú intervallum, amibe egy többszörös sem kerül. Márpedig a mindenhol sűrűséghez ez kéne. np többszörösei pedig természetesen nem sűrűek R-ben. Az np+k már igen. Továbbra is fenntartom, hogy a mindenhol való sűrűséghez kell, hogy p mint irracionális szám, elsőrendűnél jobban legyen közelíthető racionálisan. Egyébként a te bizonyításodban hol használjuk ki, hogy p irracionális? Mert ha p racionális, akkor is igaz lehet amit mondasz (lesz két olyan np és kp amelyek egy intervallumba esnek).
|
| Előzmény: [2917] jonas, 2009-04-19 15:14:31 |
|
| [2917] jonas | 2009-04-19 15:14:31 |
 Azt szerintem is ki kell használni, hogy ha p irracionális, akkor {floor(np)} sűrű a [0..1] intervallumon. Erre viszont én egy másik bizonyítást találok természetesnek, mégpedig a következőt.
Rögzítsük a 0< számot. Osszuk fel a [0..1] intervallumot 1/ számot. Osszuk fel a [0..1] intervallumot 1/ egyforma részre: [0.. egyforma részre: [0.. ],[ ],[ ..2 ..2 ],...,[floor(1/ ],...,[floor(1/ ) ) ..floor(1+1/ ..floor(1+1/ ) ) ], mindegyik ], mindegyik  hosszú. Vegyük most a p első 1/ hosszú. Vegyük most a p első 1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ )p számokat. Ezek mindegyike 0 és 1 közé esik, és annyi van belőlük, mint intervallum, így kell lennie egy intervallumnak, ahova kettő esik. Ennek a két többszörösnek a különbsége abszolutértékben legfeljebb )p számokat. Ezek mindegyike 0 és 1 közé esik, és annyi van belőlük, mint intervallum, így kell lennie egy intervallumnak, ahova kettő esik. Ennek a két többszörösnek a különbsége abszolutértékben legfeljebb  , legyen ez a különbség mondjuk 0<floor(np)< , legyen ez a különbség mondjuk 0<floor(np)< (ahol n lehet pozitív vagy negatív, de nem nulla). Ekkor vehetjük egyszerűen np többszöröseit, és ezek is (ahol n lehet pozitív vagy negatív, de nem nulla). Ekkor vehetjük egyszerűen np többszöröseit, és ezek is  sűrűek. sűrűek.
|
| Előzmény: [2915] jenei.attila, 2009-04-19 14:17:32 |
|
| [2916] lorantfy | 2009-04-19 15:08:06 |
 500. feladat: Egy bank páncélszekrényén 6 zár van. Kulcsaikat úgy osztották el a 4 pénztáros között, hogy a páncélszekrény kinyitásához legalább hármójuknak jelen kell lennie, de mind a négynek nem. Egy zárhoz többüknél is van kulcs, illetve egy pénztárosnál több kulcs is van. Hány olyan kulcselosztás van, melynél mindegyik pénztáros ugyanannyi kulccsal rendelkezik?
|
|





 . Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}<
. Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}<
