| [316] Csimby | 2004-04-16 21:46:51 |
 71.feladat Színezzük a sakk tábla mezőit tetszőleges módon két különböző színnel. Bizonyítsuk be, hogy az egyik színre színezett mezők bejárhatók egy királynővel (átlósan, vízszintesen és függőlegesen tud mozogni), úgy, hogy a királynő áthaladhat a másik színre színezett mezők felett, de azokon nem állhat meg! Egy mezőn többször is áthaladhat.
|
|
| [315] lorantfy | 2004-04-15 22:24:35 |
 Kedves NádorP!
A b) rész 2. felében Neked van igazad. Én elkapkodtam. Nem elég a sort és az oszlopot kiválasztani... A bástyás példa szemléletesen mutatja, hogy itt még 72 megoldás van, tehát a páratlan esetben összesen 88.
|
| Előzmény: [313] nadorp, 2004-04-15 14:42:46 |
|
| [314] nadorp | 2004-04-15 14:45:01 |
 Kedves László !
Most láttam, hogy Te is válaszoltál. A páratlan esetben különbözünk, majd én átgondolom a megoldást.
N.P.
|
|
| [313] nadorp | 2004-04-15 14:42:46 |
 Sziasztok !
Egyelőre csak a konkrét esettel foglalkoztam, a szimmetrikus,elforgatott megoldásokat különbözőnek tekintettem.
a) Legyen minden sorban és oszlopban páros sok korong. Ez csak úgy lehet, ha 2 sorban 4 korong és 1 sorban 2 van vagy 1 sorban 4 korong és háromban kettő. Az első eset nem fordulhat elő, mert ekkor két oszlopban is három korong lenne.Ezért marad a második lehetőség, de ekkor ugyanígy egy oszlopban 4 korong és 3 oszlopban 2 korong van. Válasszunk ki egy sort és egy oszlopot, ahol 4 korong lesz. Ezt megtehetjük 16-féleképpen.Tekintsünk egy, a kiválasztott sortól különböző sort. Ide 3 helyre tehetünk korongot.Ezek után még egy, az előzőektől különböző sort tekintve már csak két lehetőség közül választhatunk.Így az összes esetek száma 16.3.2=96.
b)Legyen minden sorban és oszlopban páratlan sok korong. Ez csak úgy lehet, ha 3 sorban és oszlopban 3 korong van, és egy sorban és egy oszlopban egy korong van.Válasszunk ki egy sort és egy oszlopot, ahol 1 korong lesz. Két eset lehetséges. Ha a kiválasztott sorban és oszlopban összesen csak 1 korong van, akkor a maradék összes, nem kizárt 9 mezőre kerül korong. Ez összesen 16 eset.Ha a kiválasztott sorban és oszlopban összesen 2 korong van, akkor könnyen látható,hogy a két korong által meghatározott sorok és oszlopok másik két kereszteződésében nem lehet korong.Így 8 mezőre kell 8 korongot elhelyezni, azaz a kiválasztott 2 korong egyértelműen meghatározza a többi helyzetét. Az esetek száma annyi, ahányféleképpen el lehet helyezni két bástyát egy 4x4 sakktáblán úgy, hogy ne üssék egymást.Egy bástyához 9-féleképpen lehet másikat feltenni, ez összesen 9.16=144 eset, de mindegyiket kétszer számoltuk. Azt kaptuk tehát, hogy páratlan esetek száma 16+72=88.
Remélem nem bonyolítottam ( és nem számoltam) el.
N.P.
|
| Előzmény: [310] lorantfy, 2004-04-15 12:54:58 |
|
| [312] lorantfy | 2004-04-15 14:41:17 |
 Kedves Károly!
Ügyes ki példa ez, csak kevés az időm.
Megoldások száma a 70. feladatnál:
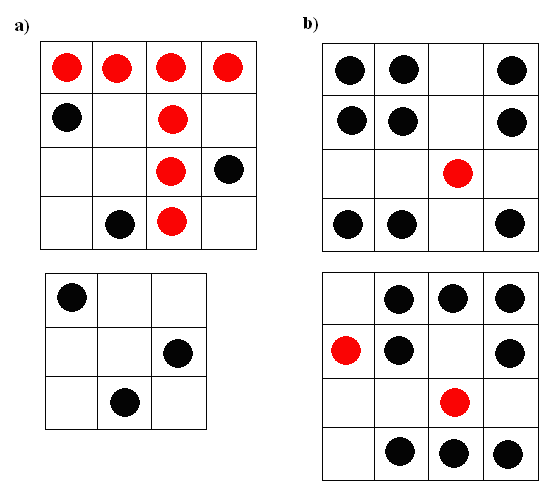
a) esetben 10=4+2+2+2. Nézzük először a 4-es sorok és oszlopok helyzetét. Bármelyik sor bármelyik oszloppal párosítható. Ez 16 lehetőséget jelent, de minden elrendezésnél még 3 korong helyét variálhatjuk. A megmaradó 3x3-as négyzetrácsban kell elhelyeznünk a 3 korongot, úgy, hogy minden sorban és oszlopban csak 1 lehet. Ez 6 féleképpen lehetséges. Így a megoldások száma 6x16=96.
b) esetben, csak a 10=3+3+3+1 felbontás lehetséges, így azokat a megoldásokat könnyen összeszámolhatjuk, ahol a sorban és oszlopban egyedülálló ugyanaz a korong, ami bármelyik mezőben állhat, ez 16 megoldást jelent.
De sajnos vannak olyan esetek is mikor a sorban egyedülálló koron egy oszlopban álló 3-as része és az oszlopban egyedül alló egy sorban álló 3-as része. Ezek az egyedülálló korongok bármelyik sor és oszlop párban állhatnak, ha jól gondolom akkor ez is 16 eset. Összesen 32 megoldás.
Azért jó lenne, ha utánnagondolnátok, mert ez nagyon kapkodva született! Vannak asszimmetrikus megoldások.
|
 |
| Előzmény: [311] Hajba Károly, 2004-04-15 13:05:26 |
|
|
| [310] lorantfy | 2004-04-15 12:54:58 |
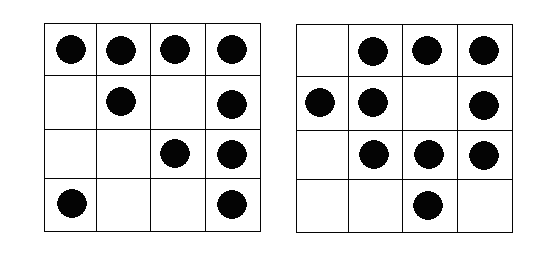
 70. feladat megoldása: Egyenlőre csak beraktam a korongokat a négyzetrácsba. Most még ki kéne találni hány megoldás van! Aztán általánosítani nxn-es rácsra és k<n2 korongra. Mikor oldható meg egyáltalán?
|
 |
| Előzmény: [309] Hajba Károly, 2004-04-15 07:47:30 |
|
| [309] Hajba Károly | 2004-04-15 07:47:30 |
 70. feladat
Adott egy fehér 4*4-es négyzetrács és 10 db fekete korong. Helyezzük el a korongokat egy-egy négyzetre az alábbi feltételek szerint:
a) minden sorban és oszlopban páros korong legyen.
b) minden sorban és oszlopban páratlan korong legyen.
HK
|
|
| [308] Hajba Károly | 2004-04-14 01:37:05 |
 Kedves Sirpi és Csimby!
Köszi a pontosítást, s mivel tetszett a feladat, elmélázatam az általánosításán is. Íme az általános megoldóképlet a maximumértékre, ahol N pozitív egész:
![f(N)=3^{\Big[\frac{N-2}{3}\Big]}*\Big(2+3*\Big\{\frac{N-2}{3}\Big\}\Big)](keplet.cgi?k=2B0BB2181C2EA873)
HK
|
| Előzmény: [307] Sirpi, 2004-04-12 15:16:43 |
|
| [307] Sirpi | 2004-04-12 15:16:43 |
 Valóban a 3668 a maximum, nézzük is, miért.
Tegyük fel, hogy felosztottuk a 2004-et néhány pozitív egész szorzatára.
Ha van a számok közt 1-es, akkor egy másik k számmal összevonva 1.k<1+k miatt növeljük a szorzatot.
Ha van olyan k szám köztük, ami legalább 4, akkor nem rontunk, ha k-t kicseréljük 2.(k-2)-re, sőt, k 4 esetén jav³tunk is. 4 esetén jav³tunk is.
Így feltehető, hogy csupa 2-es és 3-as tényezőkből áll a szorzat. De mivel 2.2.2<3.3 és 2+2+2=3+3, így legfeljebb 2 db. 2-es lehet az optimális szorzatban. De a 2004 osztható 6-tal, ami miatt a 2-esek száma 3-mal osztható kell legyen. De 0 és 2 közt csak a 0 osztható 3-mal, így az optimális szorzatban 0 db 2-es és 668 db. 3-as kell legyen.
Nem láttam be, de triviális, hogy valóban van maximum...
S
|
| Előzmény: [306] Hajba Károly, 2004-04-12 01:45:34 |
|









 4 esetén jav³tunk is.
4 esetén jav³tunk is.