| [724] Atosz | 2005-01-18 23:11:16 |
 Kedves Viktor!
Sajnos nem jó a válasz! Ennél azért egy kicsit bonyolultabb ez a feladat. Először 1 "őrültre" próbáld megoldani. Gondold végig, hogy sorba állnak az ajtónál, elől az 1-es, majd a 2-es... végül pedig a 100-as. Most az 1-es az "őrült" (gondolom érzed, hogy a sorszámozásnak nincs jelentősége), aki berohan és leül pl. a 38-as székre. Ekkor 2-37-ig nincs gond, ám jön a 38-as akinek foglalt a helye...Ha az "őrült" a 100-as helyére ült volna, akkor 0 valséggel ül a helyére a 100-as. Ezt a gondolatmenetet kövesd '38' nélkül általánosan.
Egy darabig még hagyok időt mindenkinek - aztán közzéteszem a megoldást!
Minden jót: Atosz
|
| Előzmény: [723] xviktor, 2005-01-18 18:13:48 |
|
| [723] xviktor | 2005-01-18 18:13:48 |
 Hello Atosz!
Szerintem a feladat kissé egyszerűbb. Véleményem szerint az mindegy, hogy hány őrült van köztük, és szerintem annak az esélye, hogy a 100. utas a helyére tud ülni mindig 1/n, így 100 utasnál 0,01.
Üdv: Viktor
|
| Előzmény: [721] Atosz, 2005-01-17 23:26:18 |
|
|
| [721] Atosz | 2005-01-17 23:26:18 |
 Kedves Lóczi Lajos és többiek!
Egész ügyes ez a Mathematica, a képlet tényleg zártabb, és módot ad p2,k egy elég jó felső becslésére.
Előszedtem a harmonikus sor és a számtani közép közti egyenlőtlenséget, miszerint:
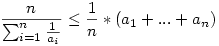
Itt most n=k+2 és ai=i, amit ha elkezdünk alakítgatni, kapjuk, hogy
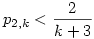
Szeretnék azoknak akiknek nem fekszik teljesen ez a gyógyszeres feladat egy új példát adni a valség köréből, ami nem túl nehéz, ám a megoldása miatt az egyik kedvencem:
100 utas várakozik a reptéren, hogy végre beszállhassanak. A gépen 100 ülőhely van, mindenkinek máshová szól a jegye. Az első utas "őrült" nem törődik a jegyével, s beszálláskor véletlenszerűen elfoglal egy széket. Az összes többi utas "normális" és a helyére fog ülni, feltéve, ha ott még nem ül senki. Ha a helyük foglalt, akkor ők is véletlenszerűen választanak egy széket. (az utasok egymás után egyesével szállnak a gépre)
Mekkora a valsége annak, hogy a 100. utas a helyére tud ülni? Mi a helyzet n utas és abból k őrült esetén?
|
| Előzmény: [720] Lóczi Lajos, 2005-01-17 17:51:35 |
|
| [720] Lóczi Lajos | 2005-01-17 17:51:35 |
 A Mathematicába beírtam a p2,k-ra vonatkozó rekurzív képletet, és az alábbi alakot kaptam vissza, ami talán kicsit egyszerűbb, mint az említett:
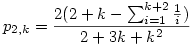
Látható, hogy a (k+2)-edik harmonikus szám szerepel a képletben, tehát ennél "zártabb" alak p2,k-ra szerintem nem várható.
|
| Előzmény: [719] Atosz, 2005-01-17 16:52:17 |
|
| [719] Atosz | 2005-01-17 16:52:17 |
 Sziasztok!
Újabb "Rés a pajzson..." a gyógyszeres feladatban. Kis lépés, de ez is valami.
Sokáig próbálkoztam a pk,k vizsgálatával de nem bírtam zárt, "szumma" nélküli alakra hozni. Arra gondoltam, hátha alulról építkezve, speciális eseteket vizsgálva érnénk el eredményt.
Megnéztem a p1,k (1 egész, k fél) valségét. Ilyenkor abban az esetben marad egész, ha végig feleket húzunk egymás után, azaz
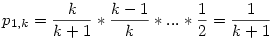
Ekkor felírtam p2,k-ra az eredeti rekurziós képletet, azaz:
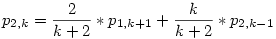
Beírva p1,k+1 helyére az 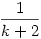 értéket, kapjuk hogy: értéket, kapjuk hogy:
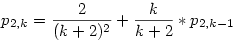
Rengeteg egyváltozós függvényt vizsgáltam meg, hogy eleget tesz-e az előző függvényegyenletnek, de nem jártam sikerrel. Ekkor p2,k-1-et tovább alakítottam p2,k-2-vé és így tovább, amíg el nem érünk p2,0-ig, melynek értéke 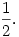 A kapott hosszú szörnyet addig néztem, amíg ki nem jött, hogy: A kapott hosszú szörnyet addig néztem, amíg ki nem jött, hogy:
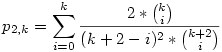
Jó lenne ennek egy zárt alakot felírni, de nekem már ez is tetszik. Viszonylag jól lehet vele számolni is:
pl. 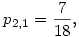 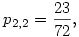 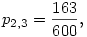
További jó munkát!
|
|
| [718] Bubu | 2005-01-17 15:13:44 |
 Hello Mindenki!
A kihalási probléma a következő: Egy szigetre egy férfi érkezik. A szigeten tetszőleges mennyiségben rendelkezésre állnak nők (19. századi a feladat). Egy férfi p(0) valséggel 0, p(1) valséggel 1, stb., p(n) valséggel n nemzőképes fiú utódot hoz létre (Ezen valségek összege 1.). Mi a valószínűsége, hogy a populáció véges idő alatt kihal?
Szerintem nem sok köze van egymáshoz a kettőnek. Az biztos, hogy a kihalási problémára is felírható egy rekurzió, ami nem oldható meg, és ott az trükk, hogy a generátorfüggvény kompozicóit kell vizsgálni. Sajnos töbet nem tudok én se róla, mert csak egy rövid folyosói beszélgetésben hallottam a problémáról, de ha kell majd utánakérdezek később. Nem tudom, hogy ezzel segítettem-e, mindenesetre most nem érek rá ezzel foglalkozni, mert analízis szigorlatra készülök gőzerővel.
Üdv: Bubu
|
|
| [717] Atosz | 2005-01-15 00:22:21 |
 Sziasztok!
Visszatérve a gyógyszeres feladathoz, sikerült előtúrnom a régi jegyzeteimet, a benne lévőket közreadom, hátha közös erővel közelebb jutunk a megoldáshoz.
Kézi erővel viszonylag egyszerű a gyógyszerfogyási fát felírni. Pl. n=4-re - írjuk ezt úgy, hogy (4,0) -, ebből előbb (3,1) lesz, majd növesztjük az ágakat: 3/4 valséggel megyünk (2,2)-re és 1/4 valséggel (3,0)-ra. Ezt egészen addig folytatjuk, amíg a fa ágainak végén 1 egész, vagy 1 fél szem lesz. Összeszorozzuk az egész végű ágon lévő valségeket, majd az ilyen ágak értékeit összeadjuk, megkapjuk a keresett valószínűséget.
Ha sehol sem számoltam el, akkor n=2-re p=1/2, n=3-ra p=7/18, és n=4-re p=97/288. Persze ember legyen a talpán, aki mindezt sz.gép nélkül n=100-ra megcsinálja.
Ekkor elkezdtem az ált. problémát vizsgálni. Legyen 'e' az egész, míg 'f' a fél szemek száma. Annak a valószínűsége, hogy ebből egész marad, az legyen pe,f. Az általános rekurzív formula így:
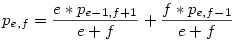
Ezt több oldalon keresztül alakítgattam, de nem bírtam vele. Ekkor elkezdtem egy picit specializálni, és megvizsgáltam azt az esetet, amikor induláskor megegyezik az egész és a felek száma, azaz megnéztem pk,k-t. Annak reményében tettem mindezt, hátha ezek segítségével jutunk az ált. eset nyomára.
Sikerült egy szép zárt alakot felírnom (ami még mindig rekurzív, de már lemegy 1-ig)
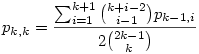
Ez pl. p4,4-re: (és a nevezővel átszorozva)
70*p4,4=35*p3,5+20*p3,4+10*p3,3+4*p3,2+p3,1
Egyelőre ennyi. Szerintem ez egy igen érdekes probléma, ne adjuk fel, előbb utóbb meglesz!
|
| Előzmény: [716] jenei.attila, 2005-01-14 13:40:18 |
|
|
| [715] jenei.attila | 2005-01-14 13:35:26 |
 Ezzel szerintem az a baj, hogy feltételezed, bármely sorozat előfordulása ugyanolyan valószínű, holott ez nem igaz. A kedvező eset/összes eset képlet pedig csak ekkor alkalmazgató. A képleted sajnos n=2 re sem jó, mert 1/3-ot ad, a helyes érték pedig 1/2.
|
| Előzmény: [714] nadorp, 2005-01-14 13:05:26 |
|





 -hoz.
-hoz.