Fórum: Érdekes matekfeladatok

1-1/e.

Sziasztok,

Szerintem az őrült utasos feladatot még ne zárjuk le. Keressünk közvetlen, számolás nélküli megoldást.

Sziasztok!

Itt az újabb példa, szintén a valség köréből (A feladat Mikulás-probléma néven is ismert).

Egy 'n' fős osztályban Mikulás ünnepségre készülnek a gyerekek. A tanár mindenkinek felírja a nevét egy cetlire, majd beteszi egy kalapba és ezután kezdődik a húzás. Miután mindenki kihúzott egyet, mi a valószínűsége annak, hogy senki sem húzta a saját nevét, azaz nem kell kezdeni mindent előről?

Kiegészítés: előzőleg külön kezeltük azt az esetet, amikor az utolsó utas őrült, mondván, hogy a keresett valószínűség ekkor ugyanaz, mint amikor k-1 őrült van. Ugyanis nem befolyásolja az eseményeket, hogy az utolsó utas őrült vagy sem, mivel csak az egyetlen megmaradt helyre tud ülni. Összefoglalva tehát: n utas és ezek közül bármely k őrült utas esetén (n>=k) annak valószínűsége hogy az utolsó utas a helyére ül 1/(k+1), ha az utolsó utas nem őrült, és 1/k, ha az utolsó utas őrült.

Tegyük fel, hogy n utas van, és ezek közül az i₁,i₂,...,i_k (ahol 1<=i₁<i₂<...<i_k<=n) sorszámú utasok őrültek. Jelöljük p_n(i₁,i₂,...,i_k)-val annak valószínűségét, hogy az utolsó utas a helyére tud ülni. Tegyük fel, hogy a szóban forgó valószínűségeket már ismerjük n-nél kevesebb utas és ezek közül bármely k,k-1,k-2,...,1 őrült esetén. Világos, hogy ekkor már csak a p_n(1,i₂,...,i_k) alakú valószínűségeket kell kiszámolni, mivel i₁>1 esetén a keresett valószínűség p_n-i1+1(1,i₂-i₁+1,...,i_k-i₁+1) (hiszen az első i₁-1 utasig rendben mennek a dolgok), amit a feltevés szerint már ismerünk. Természetesen ahhoz, hogy egyáltalán ilyen módon k őrült esetén el tudjunk indulni, ismerni kell a p_k+1(1,i₂,...,i_k) valószínűségeket (ha i₁<>1, akkor p_k+1(2,3,...,k+1)=p_k(1,2,...,k)=p_k(1,2,...,k-1) valószínűségről van szó, mivel mindegy hogy az utolsó utas őrült -e vagy sem, úgyis csak az egyetlen üres helyre tud ülni). A továbbiakban egyszerűsítjük a jelölést, mivel indukcióval feltesszük, hogy k-nál kevesebb őrült esetén a valószínűség független attól, hogy pontosan mely utasok őrültek, vagyis p_n,m:=p_n(i₁,...,i_m) bármely i₁,...,i_m kombináció esetén. Mint azt egy őrült esetén láttuk, a feltevés jogos. Tehát van k+1 utasunk, az első k utas őrült. Feltehetjük, hogy az utolsó utas nem őrült, mert ez nem befolyásolja a keresett valószínűséget (így is úgy is csak az egyetlen megmaradt helyre tud ülni), ha pedig őrült lenne, akkor nyilván eggyel kevesebb őrülttel kellene megoldani a feladatot, amit már a feltevés szerint megoldottunk. Ekkor

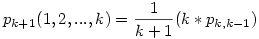
. A fenti képletben az 1. utas (aki őrült) 1/(k+1) valószínűséggel ül bármely helyre. Ha saját vagy másik őrült helyére ül, akkor a leültetendő utasok és az őrültek száma 1-gyel csökken, ezt nyilván k féleképpen teheti meg. Az egyetlen normális utas (utolsó utas) helyére nem ülhet, mert akkor biztos hogy az utolsó utas nem ül a saját helyére. Most teljes indukcióval feltesszük, hogy minden n-re, és minden m<k őrültre a keresett valószínűség 1/(m+1). Ez m=1-re már bizonyított. Ekkor a fenti képlet szerint

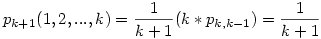
. Most rögzített k őrültszám mellett n szerinti teljes indukcióval haladunk (n>k), és feltesszük, hogy adott k mellett n-1,n-2,...,k+1 utassal a keresett valószínűség utasszámtól és őrültek kombinációjától függetlenül 1/(k+1).

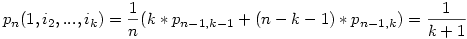
. Az első utas (aki őrült) 1/n valószínűséggel ül bármely helyre, ebből k esetben őrült helyére (a sajátját is beleértve). Ha őrült helyére ült, akkor az utasok és az őrültek száma is 1-gyel csökken, mely esetre ismerjük a valószínűséget (1/k). Ha nem őrült helyére és nem is az utolsó helyre ül (n-k-1 eset), akkor az utasok száma 1-gyel csökken, de akinek a helyére ült, az megőrül, vagyis az őrültek száma marad. Az indukciós feltevés szerint ez esetekben is ismerjük a valószínűséget (1/(k+1)). Innen n utasra és k őrültre (ahol az 1. utas biztos őrült) a keresett valószínűség 1/(k+1) és független az őrültek kombinációjától, ha n-nél kevesebb utasra is fügetlen volt (ez az indukciós feltevés).

Egy nem túl pontos,de elvi becslés a p(k,n) valószinűségre: p(k,n) legfeljebb k/(n+k).Ez (2k+n) szerinti teljes indukcióval triviális. k=0 esetén 0 pontos,k=1 esetén 1/(n+1) pontos,k=2 esetén 2/(n+2),ami nincs messze a pontostól.Sajnos ez csak 'soronként' becsül,azaz csak a nyilvánvaló állitás jön ki,hogy hogy ha felek száma végtelenbe tart,akkor a valószinűség 0-hoz.Sajnos az 'érdekes' p(n,0) határértékről semmit sem mond( csak azt, hogy p(n,0)<1).

Kedves jenei.attila!

Gratulálok a megoldásaidhoz, bár szerintem jó lenne, ha megpróbálnád leírni. (TeX-el vagy nélküle...)

Gyógyszer...

Sikerült a p_k,k-hoz hasonló zárt, de sajnos rekurzív képletet felírnom p_e,f-re, hátha valamelyikőtöknek sikerül vele valamit kezdeni:

Sok szerencsét az alakítgatásához!

Kedves Kós Géza!

Küldtem neked emilt a honlapodon lévő e-mail címekre. Légyszi nézd meg őket, és írj vissza valamit. Előre is köszönöm!

Hasonló gondolatmenettel belátható, hogy k őrült esetén a keresett valószínűség 1/(k+1), ha az emberek száma legalább k+1. Érdekes megfigyelni, hogu a valószínűség nem függ n-től, és attól sem, hogy mely utasok őrültek. Ezt teljes indukcióval lehet igazolni, de leírni kicsit bolnyolult.

Kedves rizs!

jenei.attila megoldása teljesen jó (és így "hivatalos" is), legfeljebb a vége egy picit elnagyolt.

Amiből kiindulunk az a:

Ez ugye azt jelenti, hogy minden helyre valséggel ül, a zárójelben pedig sorra 1, ha a saját helyére, p_n-1 ha a második helyére stb...

Ha felírjuk ugyanezt n-1 emberre, akkor kapjuk, hogy:

Így az első sorban a zárójelben lévő 1+p_n-2+...p₂ helyére beírhatjuk, hogy (n-1)*p_n-1 és kapjuk, hogy

n*p_n=n*p_n-1

Ez azt jelenti, hogy minden p_i egyforma, azaz

Persze még hiányzik az n utas és k őrült esete.

Ami a határértéket illeti,fogalmam hogy sincs hogy mennyi,vagy hogy létezik-e,de az biztos hogy ha létezik a p(n,0) határérték(n tart végtelenhez),akkor minden rögzitett a esetén létezik a p(n,a) határérték és egyenlő a p(n,0) határértékével(legyen ez P).Ugyanis p(n,0)=p(n-1,1) igy a=1 esetén igaz. Indukcióval p(n,a)=p(n-1,a+1)(n/(n+a))+p(n,a-1)(a/(n+a)) A baloldal P-hez tart, a jobb oldal 2.tagja 0-hoz tart,mert a/(n+a) 0-hoz tart,mig n/(n+a) 1-hez tart,igy p(n,a) határértéke egyenlő p(n-1,a+1) határértékével,igy a p(n,a+1) határértéke egyenlő p(n,a+1) határértékével.