Fórum: Érdekes matekfeladatok

(4x+3)(x-5).3=(2x+21)(x-2).6 Vezesd le a következő lépést.Kösz

Na egy érdekes feladat:Lehet-e 6 egymást követő pozitív egész szám szorzata egy egész szám 5. hatványa?

Nem

Egy unalmas irodalomóra szüleménye!(szerintem érdekes lett)

158. feladat: Egy 6x6-os táblázatra néhány dominót helyezünk, hogy mindegyik pontosan 2 mezőt fed le. Bizonyítsuk be,hogy ha 14 mező fedetlen,akkor még egy dominót a táblára helyezhetünk,úgy hogy a többit a helyén hagyjuk!

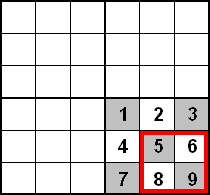
Elképzelés a 158. feladatra: Tehát próbáljunk meg 14 üres mezőt úgy elhelyezni ezen a táblázaton, hogy a maradék 22-n mind legyen dominó. Mivel 6 sorunk és oszlopunk van, belátható, hogy 2 sorban és oszlopban legalább 3 üres mező lesz. Azt kell belátnunk, hogy nem tudunk úgy elhelyezni 14 üres mezőt, hogy a nem üreseket pedig dominó fedje. Vizsgáljuk csak a sorokat! Ha az első sorban 3 üres mezőt kívánunk elhelyezni, azt kétféleképpen tehetjük meg: (D a dominóval fedett, Ü az üres mező): (1) ÜDÜDÜD (vagy ennek szimmetrikus változata) ill. (2)ÜDÜDDÜ (és ennek is a szimmetrikus változata). A szimmetrikus változatok vizsgálatát elhagyhatjuk, hiszen azok lényegében ugyanazok mint az eredetik. Először nézzük meg, hogy ha egy sorban 3 üres mező van, akkor a következő sorban mennyi üres mező lehet maximum. Az (1) esetén 0, míg a (2) esetén 0 vagy 1. Nézzük az (1) elrendezést! Ekkor a második sorban DDDDDD lesz, hiszen az első sor 1.,3.,5. kockája alatt nem lehet üres mező, mert akkor lenne üres pár, így a második sor 1.,3.,5. mezője D-s lesz, a 2.,4.,6. mező pedig az első sor dominói miatt lesznek fedettek. Tehát a maradék 4 sorban 11 üres mezőt kellene elhelyeznünk. Mivel egy sorban 0,1,2,3 üres mező lehet és a 11-et 4 tag összegeként a 0,1,2,3 segítségével csak 2+3+3+3-ként lehet felírni, ezért a maradék 4 sorból háromban is 3 üres mezőnek kell szerepelnie. De ha a 3. sorban 3 üres mező van, akkor a következőben legfeljebb egy lehet, azaz a hátramaradó kettőben 7nek kell lennie, ami lehetetlen. Ha a harmadik sorban 2 üres mező van, akkor a negyedik már biztos 3 van, de az után legfeljebb csak egy lehet az ötödikben, azaz a hatodikban 5nek kell lennie, ami szintén lehetetlen. A (2) esetben a 2. sorban a legjobb esetben 1 üres mező szerepel. Az a maradék négy sorban 10. Ez kétféleképpen írható fel a 0,1,2,3 számok 4tagú összegeként: 1+3+3+3 vagy 2+2+3+3. Erről a két lehetőségről is könnyen beláthatjuk, hogy nem lehetségesek (hasonlóan mint az (1) esetben). Ha az első sorban 2 üres mező szerepel, azzal nem változott semmi, hiszen a 2 db 3 üres mezős sor elhelyezése abban az esetben sem lehetséges. Tehát beláttuk, hogy nem lehet elhelyezni 14 üres mezőt, úgy hogy a maradék 22-n mind dominó legyen, azaz legalább egy üres mező-pár lesz, azaz elhelyezhetünk még egy dominót úgy, hogy ne kelljen elmozdítani amár lerakott dominókat. (Picit hosszú megoldás, jobb lett volna egy rövidebb, "elegánsabb", de olyat nem találtam... talán valaki más...)

Ezt a bizonyítást nem egészen értem. Az világos, hogy ha a legfelső sorban három lyuk van, akkor nem lehet a következőben egynél több. Viszont úgy tűnik, hogy a bizonyîtásban ezt nem csak az első sorra, hanem a többire is kihasználod, ezekre pedig már nem tudon, miért lenne igaz.

Őszintén szólva,én is az "elegánsabb" megoldás reményében írtam be a feladatom,mert az én bizonyításom is legalább ilyen hosszú.Ettől függetlenül én is csak az elejét értem a bizonyításodnak...(mondjuk Einsteint sem értették:) Talán vmi ábrával szemléltetve felfognánk mit mondasz!?

Szerintem bontsuk fel 4 db. 3×3-as négyzetté a 6×6-os négyzetet. Ugye 14 üres mező marad összesen, vagyis lesz olyan 3×3-as négyzet amelyben legfeljebb 5 mezőt fed le dominó (ha mindegyikben legalább 6 mezőt fedne le dominó, akkor 4×6=24, 24+14=38 > 36, ami ellentmondás).

A szimetria miatt mindegy, hogy melyik 3×3-as négyzetben bizonyítjuk, hogy ha csak 5 mezőt fedünk le belőle dominókkal, akkor még egy dominót el tudunk helyezni, tehát legyen ez a jobb alsó 3×3-as négyzet.

Ahhoz, hogy a piros négyzetben ne maradjon hely domionónak, ahhoz mindenképpen el kell helyeznünk 2 teljes dominót a 3×3-as négyzetben. Vagyis biztosan lefedünk 2 szürke és 2 fehér mezőt. Az 5. mező lefedése után tehát vagy 3 szürke és 1 fehér, vagy pedig 2 fehér és 2 szürke mezőnk marad.

Mindegyik fehér mezőnek 3 szürke szomszédja van, tehát bármely fehér mezőhöz csak 2 olyan szürke mező létezik, amely nem mellette található, így ha 3 szürke és 1 fehér mező marad üresen, akkor biztosan lesz hely még egy dominónak.

2 fehér mezőnek vagy 4 vagy 5 szürke szomszédja van, tehát akárhogy is marad üresen 2 szürke és 2 fehér mező, biztosan lesz 2 egymás melletti és így biztosan lesz hely még egy dominónak.

A számozásra végül nem lett szükség csak az elején ezt még nem tudtam...

Jonasnak igaza van, a többi sorban nem feltétlenül működik, azonban ha ott is megvizsgálnánk a további sorokat, kijönne az, hogy nem lehet üres mezőt elhelyezni... a közérthetetlenségemért meg elnézést kérek, egyszerűen csak nem tudok fogalmazni... Viszont felmerült bennem egy kérdés: Adott egy k pozitív páros szám. Egy k*k-ás táblázatban elhelyezünk néhány dominót. Melyik az a legkisebb N szám, amelyre igaz, hogy még mindenféleképpen el lehet helyezni még egy dominót, anélkül, hogy a már letett dominókat elmozdítanánk?

k=2-nél szerintem ez 2, k=4-nél talán 6, k=6-nál akkor 14.