| [211] Csizmadia Gábor | 2004-01-10 16:50:46 |
 49. feladat
Szerintem nagyon érdekes ez a feladat, már régóta foglalkoztatott a kérdés, de csak nemrég tudtam megadni rá a választ: Ismeretes, hogy bizonyos ponthalmazok diszkrét pontokból állnak, bizonyos ponthalmazok pedig nem. Diszkrét ponthalmazoknak nincs torlódási pontjuk. Ha a természetes számokat ábrázoljuk a számegyenesen, akkor azok diszkrét pontokként jelennek meg. A racionális számok számossága megegyezik a természetes számokéval, a számegyenesen mégis minden pontjuk torlódási pont. Valós számokat úgy képzeljük el, hogy folytonosan kitöltik a rendelkezésre álló számegyenest, valamint tudjuk, hogy a valós számok számossága nagyobb, mint a természetes számoké. Általában egy euklideszi tér pontjai ugyanannyian vannak, mint a valós számok. De vajon létezik-e olyan diszkrét Rn-beli (n természetes szám, tehát egyenes pontjaiból álló, síkbeli, térbeli, vagy magasabb dimenzióbeli) ponthalmaz, aminek ugyanannyi pontja van, mint ahány valós szám?
|
|
| [212] Kós Géza | 2004-01-11 15:11:06 |
 A diszkrét fogalma megengedi hogy a halmaznak legyen torlódási pontja, csak a torlódási pont nem lehet a halmazban. Például az 1,1/2,1/3,... sorozat diszkrét, pedig van torlódási pontja, a 0.
Mindkét értelmezésben igaz, hogy Rn-ben minden diszkrét halmaz megszámlálható, ezt többféleképpen is be lehet bizonyítani. Nem írom le egyik megoldást sem, csak útbaigazítást szeretnék adni.
1. megoldás: A halmaz minden pontjához rendeljünk hozzá (valahogy, ügyesen) egy olyan, közeli pontot, aminek mindegyik koordinátája racionális.
2. megoldás: Osszuk fel a teret megszámlálható sok korlátos részre, például egységkockákra, és keressünk olyan kockát, amiben a halmaznak sok pontja van.
Akinek esetleg mindez túl könnyű, annak egy nehezebb változat: Bizonyítsuk be, hogy egy f:R R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan  >0 szám, hogy minden x >0 szám, hogy minden x (a- (a- ,a+ ,a+ ), x ), x a esetén f(x)<f(a).) a esetén f(x)<f(a).)
|
| Előzmény: [211] Csizmadia Gábor, 2004-01-10 16:50:46 |
|
| [213] Hajba Károly | 2004-01-14 13:13:16 |
 Kedves gubbubu!
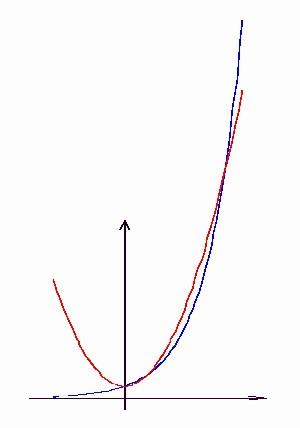
A 48. feladatra itt van az ábra, ott lent kétszer metszik egymást a görbék. Továbbá a három megoldásból két nyilvánvaló eredmény az x1=0 ill. x2=1, továbbá az általam közelítő módszerrel kiszámolt x3 4,25746. 4,25746.
|
 |
| Előzmény: [207] Gubbubu, 2004-01-06 21:14:24 |
|
| [214] Gubbubu | 2004-01-14 20:09:39 |
 Kedves Onogur, azaz Károly!
Köszönöm a megoldást, külön az ábrát. Érdekelne, hogy mivel csináltad (pl. valamilyen mat. szoftverrel, vagy egyszerűbb rajzprigrammal)? Én szabadkézi rajzzal próbálkoztam, de - amint látható - a két görbe túlságosan összeesik, így eltekintve a két triviális megoldástól és a harmadik szemmel láthatótól, nemigen látszott semmi.
Ezek után már csak két kérdés marad:
48.B. feladat: Nem lehetne valahogy algebrailag vagy számelméletileg megoldani? Megelégednék azzal is, ha csak az egész megoldásokat találnánk meg, de számolással.
48.C. feladat: Nincs-e a harmadik, nem egész megoldásnak pontos értéke, mondjuk valami egész szám logaritmusa?
Emlékeztetőül: a n2+1=2n egyenletről van szó.
|
| Előzmény: [213] Hajba Károly, 2004-01-14 13:13:16 |
|
| [215] Csimby | 2004-01-14 22:27:23 |
 Az egészek könnyen megmondhatóak: Ha n nagyobb/egyenlő kettővel, akkor (2 az n.-en), 4-gyel mindig osztható, míg n*n+1, 4-gyel osztva 1 vagy 2 maradékot ad -> marad az n=0 és n=1 eset.
|
|
| [216] Gubbubu | 2004-01-14 23:50:07 |
 Kedves Csimby;
Valóban, ez nem tűnik borzasztó nehéznek. Sőt, alighanem a 2n+1=n2 diofantikus egyenlet is hasonlóképp oldható meg. Vagyis 23 az egyetlen kettőhatvány, melyhez egyet adva a hatvány (az alap és kitevő szerepe) "megfordul".
Köszönettel: G.
|
| Előzmény: [215] Csimby, 2004-01-14 22:27:23 |
|
| [217] Hajba Károly | 2004-01-15 00:06:40 |
 Kedves Gubbubu!
A rajzolást nem egyszerűbb, de rajzprogrammal készítettem. Mérnök lévén, rendelkezésemre áll egy profi CAD program, de innentől kezdve "csaltam", mint Rodolfo. Minden egészértékhez kiszámoltam a függvényértéket és erre a koordinátahelyre pontot illesztettem, majd a pontsorra egy Bezier-görgét. A parabolát százalékos, míg a hiperbolát ezrelékes pontossággal követi. A harmadik metszéspontot 2 tizedesjegy pontossággal megadta, innen már numerikusan finomítottam az értéket.
A pótkérdéseidre nem tudok válaszolni, mivel a szakmámhoz nem szükséges matematikatudásom nem jár a fellegekben. Talán Géza vagy Sirpi mondanak valami érdekeset e témáról. :o)
HK
|
| Előzmény: [214] Gubbubu, 2004-01-14 20:09:39 |
|
| [218] Gubbubu | 2004-01-15 00:58:00 |
 Kedves Onogur!
Hűha! A Bezier-görbét nem ismerem, de a neve nem hangzik rosszul, ahogy az sem, amit az egész CAD-os eljárásról mondtál. Nem hittem volna, hogy egy ilyen, viszonylag egyszerű alakú (bár nem feltétlenül egyszerűen megoldható) egyenlet ábrázolása mögött is komoly matematika húzódhat meg. Hiába, nekem az alkalmazott matematika tudásom nem jár a fellegekben!
Ami a pótkérdéseket illeti: természetesen nem várom, hogy örökké csak az én kérdéseimre válaszolj, nagyon köszönöm az eddigi hozzászólásaidat is... csak automatikusan fölvetődtek, mint a megoldásból természetesen következő problémák.
Egyébként eme példa hatására a következő sejtés fogalmazódik meg az emberben: ahogy 4-nél magasabb fokú polinomiális egyenletek megoldására nincs gyökképlet, úgy az f(x)=xk egyenletek (f(x) k-adfokú polinom) sem oldhatóak meg alapműveletek, 2..k-adik gyökvonás és (mondjkuk k alapú) logaritmuskeresés segítségével... Úgyhogy jöhetnek a mérnökök, hajrá közelítő számítások... Soha nem hallottam, hogy ilyen témájú, azaz exponenciális-polinomiális kevert egyenletek képlettel való megoldására irányuló kutatások folytak volna valahol (bár mintha halványan emlékeznék, hogy a differenciálegyenletek elméletében van valami szerepük az ilyen egyenleteknek), de ha valaki tud valamit róluk, csak szóljon.
Viszlát mindenkinek holnap: G.
|
| Előzmény: [217] Hajba Károly, 2004-01-15 00:06:40 |
|
| [219] Hajba Károly | 2004-01-15 09:24:06 |
 Kedves gubbubu!
- A Bezier-görbék és a továbbfejlesztett változatuk a B-spline módszer 30 éve kezdett el terjedni a mérnöki számítógépes formatervezés területén. Lényege, hogy adott pontokkal leírjuk a görbét vagy térbeli felületet és a pontok közötti vonalat ill. felületet súlyozott paraméterfüggvénnyel írjuk le. Lényeges, hogy a pontokban és illeszkedési vonalakban legalább másodrendűen illeszkednek a görbék ill. felületek. A pontokkal, s illeszkedésükkel lehet globális vagy lokálisan változtatni ill. a súlyozás mértékét is lehet szabályozni a modell megjelenésén.
P. Bezier a '70-es évek legelején dolgozta ki e módszert a Renault gépkocsik formatervezésének számítógépes modellezése során, s ezt vették át más mérnöki területek is.
- A felvetetted problémán egyébként már korábban én is gondolkodtam a x2=2x formában. Ennek is két egészértékű megoldása van. Továbbá felvetésed után a következő általánosítások vetődtek fel bennem:
A görbék jellegéből adódik, hogy 1, 2 v. 3 megoldás lehetséges, s általában na+d=an alakú, ahol d lehet 0 értékű is, továbbá a és d függvényében mely d-re adódik 2 megoldás?
HK
|
| Előzmény: [218] Gubbubu, 2004-01-15 00:58:00 |
|
| [220] Gubbubu | 2004-01-16 00:46:54 |
 Üdv, Onogur,
Kösz a kimerítő (de érdekes) magyarázatot, és a történeti kiegészítést! Most már lesz min gondolkodnom a következő kb. 5 évben... Valószínűleg már az sem triviálisan látható be, hogy mindig lf. 3 metszéspont van, mert a "görbék jellege" kifejezés arra utal, hogy minimum differenciálszámítás van a háttérben. Legalábbis ilyentájt, 0:36-kor egyelőre ennyit vagyok képes látni.
Persze ki lehet tűzni a "Nehezebb matematikai problémák" rovatban ezeket az általánosításokat... hátha egyszer valaki megoldja őket... mondjuk valaki, aki "lovaszlaszlo" n.name-mel van bejelentkezve...
Üdv: G.
|
| Előzmény: [219] Hajba Károly, 2004-01-15 09:24:06 |
|




 R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan
R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan  >0 szám, hogy minden x
>0 szám, hogy minden x (a-
(a- a esetén f(x)<f(a).)
a esetén f(x)<f(a).) 
 4,25746.
4,25746. 

