| [206] lorantfy | 2004-01-06 20:50:09 |
 Kedves Attila!
Kösz a helyreigazítást. Én is rájöttem a hibára, csak már azután, hogy feltettem a hozzászólást. Hirtelen valami olyasmire gondoltam, hogy miközben x mint valós szám végigfut az adott intervallumon, a zárójelben lévő kifejezés értékei milyen egész számokat érintenek, és ezek szummája. Ez persze hülyeség, elkapkodtam!
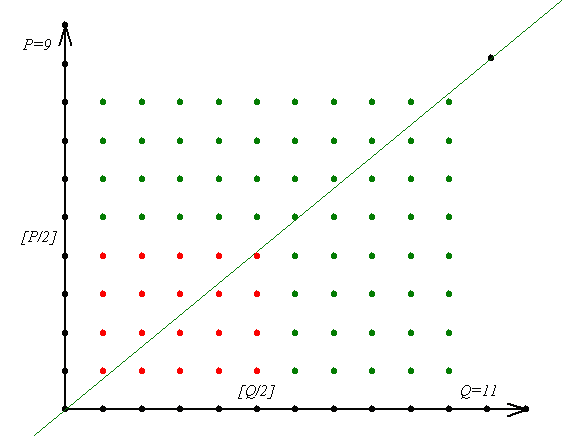
Nagyon szép és szemléletes a megoldásod! Az a fajta, amit megnéz az ember és csak fogja a fejét: - Milyen egyszerű, mért nem jutott ez nekem eszembe? Felteszek egy ábrát, hátha más is kedvet kap, hogy megnézze a hozzá tartozó feladatot és megoldást! (Lászlónak hívnak!)
|
 |
| Előzmény: [203] jenei.attila, 2004-01-05 15:27:03 |
|
| [207] Gubbubu | 2004-01-06 21:14:24 |
 Üdv!
Rövid időre megint itt vagyok.
Örülök, hogy legalább egyik feladatom megoldhatónak (tehát értelmesnek) bizonyult, remélem szereztem egy kellemes percet GJ-nek, nem hiszem, hogy tovább törte volna a fejét... köszönet a frappáns megoldásért!
Valahol a http://orange.ngszkij.hu honlapon állítólag van néhány megjegyzés e feladattal ill. általánosításaival kapcsolatban (nekem hibát jelez a Netscapem, ha odamegyek, nem tudom, pontosan hol).
Néhány hiba vagy hiányosság került az előző, 204-es hozzászólásomba (csak most tanulom a TEX-et...):
1. a második 47. feladat valójában a 48. (feltéve, ha az előzőek számozása hibamentes);
2. Eme feladatnak elsősorban az algebrai-számelméleti jellegű megoldásai érdekelnének, bár ha valaki ábrát készítene, az is szép lenne... (A feladatban az lenne az "érdekes", hogy egy hatványhoz egyet adva fordul az alap és a kitevő szerepe, jé!...)
3. A 6-ról szóló feladatban cáfolással érdemes próbálkozni, legalábbis valós számokból álló számtani sorozatok esetében. Ha a kérdéses számtani sorozat tagjai-elemei számát 2-re ill. 3-ra korlátozzuk, "kellemes" kis polinomgyök-keresési ill. diofantikus problémákat kapunk, nem muszáj rögtön az egész feladatot teljesen általánosan megoldani...
Megjegyzem, nyithatnánk egy Érdekes matematikai feladatok II. topicot az eddig megoldatlan feladatokat összegyűjtendő, mert kezd a dolog áttekinthetetlenné válni...
|
|
| [208] Csimby | 2004-01-07 00:07:28 |
 Legyen a számtani sorozat 1. eleme: a, differenciája d, ekkor az első n+1 elem összege: a+(a+d)+(a+2d)+(a+3d)+...+(a+nd)=(n+1)a+(n(n+1)/2)d=(n+1)(a+(n/2)d). T.F.H. ez egyenlő a szorzatukkal: (n+1)(a+(n/2)d)= a(a+d)(a+2d)(a+3d)...(a+nd) Osszunk le (a+(n/2)d)-vel: (ha n páratlan akkor ez nem szerepel a jobb oldalon,de végig lehet gondolni, hogy így is jó). n+1=a(a+d)(a+2d)...(a+(n/2-1)d)(a+(n/2+1)d)...(a+nd) ha d=0, akkor trivi, nézzük most d>1-et, ekkor: a+nd>a+n. a=0 trivi. Ha a>=1 akkor a+n>=n+1 -> a+nd>n+1, és mivel a szorzatban minden tag >=1, a szorzat nagyobb lesz a bal oldalon maradt (n+1)-nél (hiszen a jobb oldalon szerepel (a+nd) mint szorzó tényező) Maradt a d=1 eset. a+nd=a+n,csak akkor ha a szorzásban a többi tényező 1 -> n=2, a=1
|
|
|
|
| [211] Csizmadia Gábor | 2004-01-10 16:50:46 |
 49. feladat
Szerintem nagyon érdekes ez a feladat, már régóta foglalkoztatott a kérdés, de csak nemrég tudtam megadni rá a választ: Ismeretes, hogy bizonyos ponthalmazok diszkrét pontokból állnak, bizonyos ponthalmazok pedig nem. Diszkrét ponthalmazoknak nincs torlódási pontjuk. Ha a természetes számokat ábrázoljuk a számegyenesen, akkor azok diszkrét pontokként jelennek meg. A racionális számok számossága megegyezik a természetes számokéval, a számegyenesen mégis minden pontjuk torlódási pont. Valós számokat úgy képzeljük el, hogy folytonosan kitöltik a rendelkezésre álló számegyenest, valamint tudjuk, hogy a valós számok számossága nagyobb, mint a természetes számoké. Általában egy euklideszi tér pontjai ugyanannyian vannak, mint a valós számok. De vajon létezik-e olyan diszkrét Rn-beli (n természetes szám, tehát egyenes pontjaiból álló, síkbeli, térbeli, vagy magasabb dimenzióbeli) ponthalmaz, aminek ugyanannyi pontja van, mint ahány valós szám?
|
|
| [212] Kós Géza | 2004-01-11 15:11:06 |
 A diszkrét fogalma megengedi hogy a halmaznak legyen torlódási pontja, csak a torlódási pont nem lehet a halmazban. Például az 1,1/2,1/3,... sorozat diszkrét, pedig van torlódási pontja, a 0.
Mindkét értelmezésben igaz, hogy Rn-ben minden diszkrét halmaz megszámlálható, ezt többféleképpen is be lehet bizonyítani. Nem írom le egyik megoldást sem, csak útbaigazítást szeretnék adni.
1. megoldás: A halmaz minden pontjához rendeljünk hozzá (valahogy, ügyesen) egy olyan, közeli pontot, aminek mindegyik koordinátája racionális.
2. megoldás: Osszuk fel a teret megszámlálható sok korlátos részre, például egységkockákra, és keressünk olyan kockát, amiben a halmaznak sok pontja van.
Akinek esetleg mindez túl könnyű, annak egy nehezebb változat: Bizonyítsuk be, hogy egy f:R R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan  >0 szám, hogy minden x >0 szám, hogy minden x (a- (a- ,a+ ,a+ ), x ), x a esetén f(x)<f(a).) a esetén f(x)<f(a).)
|
| Előzmény: [211] Csizmadia Gábor, 2004-01-10 16:50:46 |
|
| [213] Hajba Károly | 2004-01-14 13:13:16 |
 Kedves gubbubu!
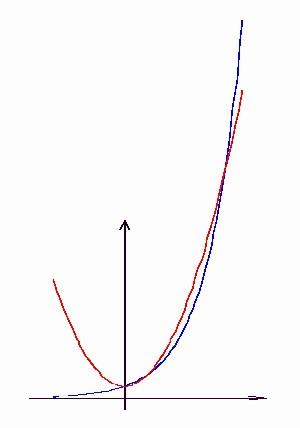
A 48. feladatra itt van az ábra, ott lent kétszer metszik egymást a görbék. Továbbá a három megoldásból két nyilvánvaló eredmény az x1=0 ill. x2=1, továbbá az általam közelítő módszerrel kiszámolt x3 4,25746. 4,25746.
|
 |
| Előzmény: [207] Gubbubu, 2004-01-06 21:14:24 |
|
| [214] Gubbubu | 2004-01-14 20:09:39 |
 Kedves Onogur, azaz Károly!
Köszönöm a megoldást, külön az ábrát. Érdekelne, hogy mivel csináltad (pl. valamilyen mat. szoftverrel, vagy egyszerűbb rajzprigrammal)? Én szabadkézi rajzzal próbálkoztam, de - amint látható - a két görbe túlságosan összeesik, így eltekintve a két triviális megoldástól és a harmadik szemmel láthatótól, nemigen látszott semmi.
Ezek után már csak két kérdés marad:
48.B. feladat: Nem lehetne valahogy algebrailag vagy számelméletileg megoldani? Megelégednék azzal is, ha csak az egész megoldásokat találnánk meg, de számolással.
48.C. feladat: Nincs-e a harmadik, nem egész megoldásnak pontos értéke, mondjuk valami egész szám logaritmusa?
Emlékeztetőül: a n2+1=2n egyenletről van szó.
|
| Előzmény: [213] Hajba Károly, 2004-01-14 13:13:16 |
|
| [215] Csimby | 2004-01-14 22:27:23 |
 Az egészek könnyen megmondhatóak: Ha n nagyobb/egyenlő kettővel, akkor (2 az n.-en), 4-gyel mindig osztható, míg n*n+1, 4-gyel osztva 1 vagy 2 maradékot ad -> marad az n=0 és n=1 eset.
|
|










 R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan
R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan  >0 szám, hogy minden x
>0 szám, hogy minden x (a-
(a- a esetén f(x)<f(a).)
a esetén f(x)<f(a).)  4,25746.
4,25746. 