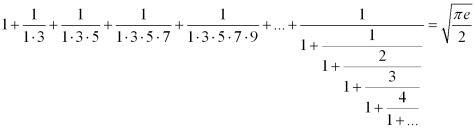| [1022] Yegreg | 2005-08-16 17:36:10 |
 A hatszöges feladatra írt képlet így jött ki: Vagyünk 3 szomszédos csúcsot, és a két szélsőt kössük össze a 120°-os forgásszimmetria középpontjával. Ekkor a forgásszimmetria miatt(bármelyik 3 egymás melletti csúcsot választjuk) a hatszög területének 3-ada lesz a kapott négyszög területe. Ez eddig a külső 3-as szorzó, a zárójelben a négyszög területe van. A négyszög oldalai: 2, 4, a, a. Az első kettő a hatszög két oldala a másik kettő a szimmetria miatt egyenlő. Kössük össze egymással a két szélső pontot, ekkor a négyszög egy átlóját kapjuk, ami két háromszögre bontja a négyszöget, a külső egyértelműen meghatározott adott  belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor
t1=4sin
. A behúzott átló legyen b! Ekkor b2=22+42-16cos a koszinusz tétel alapján. Ha behúzzuk a belső háromszög magasságát, akkor két egybevágó félszabályos háromszöget kapunk, ahol a nagyobb befogó a koszinusz tétel alapján. Ha behúzzuk a belső háromszög magasságát, akkor két egybevágó félszabályos háromszöget kapunk, ahol a nagyobb befogó 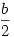 , a kisebb pedig így , a kisebb pedig így  , ami a belső háromszög magassága. A belső háromszög területe tehát , ami a belső háromszög magassága. A belső háromszög területe tehát

(valóban egyszerűsíthetünk). A hatszög területe pedig:
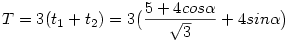
Ennyi. Üdv:
Yegreg
|
|
| [1021] xviktor | 2005-08-16 17:17:14 |
 A 189. feladat megoldasa szerintem:
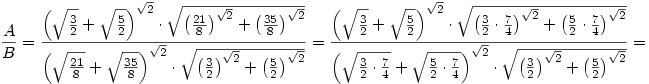
![=\frac{{\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac74\right)^{\sqrt2}\cdot \left[\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}\right]}}}{{\left[\sqrt{\frac74}\cdot\left(\sqrt{\frac32}+\sqrt{\frac52}\right)\right]^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}}=\frac{{\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}\cdot\sqrt{\left(\frac74\right)^{\sqrt2}}}{{\left(\sqrt{\frac74}\right)^{\sqrt2}\cdot\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}}=1](keplet.cgi?k=DF34C505BB17548F)
Eszreveheto, hogy az egyszerusitesek utan 1et kapunk. Igy A=B.
Amennyiben valamit elirtam legyszives szoljatok, es kijavitom.
Remelem jo a megoldasom: Viktor
|
| Előzmény: [1020] Lóczi Lajos, 2005-08-16 15:00:38 |
|
| [1020] Lóczi Lajos | 2005-08-16 15:00:38 |
 A különböző gyökkitevők egy összegben felcserélhetők?
189. feladat. Jelölje
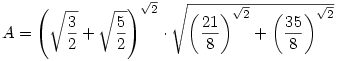
és
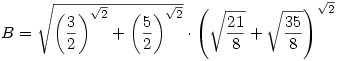
Döntsük el (majd bizonyítsuk be), hogy kettejük közül melyik a nagyobb szám.
|
|
| [1019] Lóczi Lajos | 2005-08-16 14:48:19 |
 Aki szeret térfogatot számolni, annak álljon itt a
188. feladat. Legyen a>0 adott szám és tekintsük a közönséges térbeli x-y-z koordinátarendszert.
Mekkora a térfogata annak a testnek, amely az x2+y2+z2 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2 a2 (végtelen) henger metszeteként áll elő? a2 (végtelen) henger metszeteként áll elő?
|
|
|
|
| [1016] xviktor | 2005-08-15 23:28:27 |
 Annyibban igazad van, hogy tobb eset van, tehat egy altalanos kepletet keresunk, de szerintem nem jo a kepleted... bar lehet en tevedek
Es akkor a 187. feladat: a hatszog kore kor irhato. Mekkora a terulete?
Udv: Viktor
|
| Előzmény: [1015] xviktor, 2005-08-15 23:14:22 |
|
|
| [1014] Yegreg | 2005-08-15 21:01:22 |
 Bocsánat, úgy tűnik, hogy most sem vagyok képes normálisan beírni... egy zárójel elcsúszott. Helyesen így:
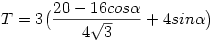
. Hiába, még nem vagyok rutinos TeX-es...:oD. Üdv:
Yegreg
|
|
| [1013] Yegreg | 2005-08-15 20:58:07 |
 Üdv!
Bocs, hogy csak most írok, de most értem haza, így nem tudtam reagálni a közbenső dolgokra. A beírt gömb sugara jogos, az egyenletet nem ismertem, kitalálni meg akkor este esélyem sem volt, pláne, hogy nem is gondolkoztam ilyesmiben(a bizonyítás amúgy nagyon szép szerintem). A sok számolás azért nem annyira sok, csak egy finom túlzás volt annak eltitkolása érdekében, hogy képtelen lettem volna beírni akkor este:). Valójában azt hiszem, hogy az pár Pitagorasz-tétel volt.
Az a hatszöges feladat nem akar összejönni Viktornak:) Vagy direkt csináltad először nem létezőre másodjára pedig több esetesre? Szóval a 186(azt hiszem) feladat megoldása:
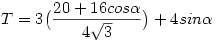
Ahol alfa valamelyik belső szög. A 120°-os forgásszimmetria nem határozza meg egyértelműen a hatszöget, csak 3-3 belső szöge egyenlő egymással, két különböző belső szög összege pedig 240°. Egyébként szerintem a feladat normálisan körbe írt hatszög lenne. Akkor egyértelműen  =120°, és akkor kiszámolható a terület(akkor máshogy is számolható). Üdv: =120°, és akkor kiszámolható a terület(akkor máshogy is számolható). Üdv:
Yegreg
|
|
| [1012] xviktor | 2005-08-14 17:59:30 |
 Gratulalok, mindenki megoldasa helyes. De a 186. feladatra meg nem jott megoldas...
Jo gondolkozast: Viktor
|
|
| [1011] lorantfy | 2005-08-14 16:26:14 |
 185-höz: Kössük össze a poliéder csúcsait a beírt gömb középpontjával. Így a poliéder térfogatát sokszög alapú gúlák térfogatának összegére bontottuk, melyek magassága éppen a beírt kör sugara, alapjaik területének összege pedig a poliéder felszine.
Igy aztán: 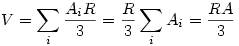
|
| Előzmény: [1010] xviktor, 2005-08-13 01:19:00 |
|
| [1010] xviktor | 2005-08-13 01:19:00 |
 Gratulalok szepek a megoldasaid /181,182,183/, a 184-et meg atgondolom en kicsit maskepp csinaltam,de szerintem az is jo.
A 183. feladatnal irtad hogy sok szamolas volt, pedig nagyon egyszeruen meg lehet allapitani a beirt gomb sugarat:
Tetel: Barmely poliederbe beirt gomb sugara: 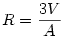
185. feladat: Bizonyitsuk be a fenti tetelt.
186. feladat: A 181. feladatot kisse fogalmazzuk at. Ha ahelyett hogy kor irhato bele azt mondanam, hogy 120°os forgasszimmetrikus, akkor mekkora lenne a terulete? /Ilyen hatszog letezik ;-)/
Jo gondolkodast: Viktor
|
| Előzmény: [1009] Yegreg, 2005-08-13 00:49:02 |
|
| [1009] Yegreg | 2005-08-13 00:49:02 |
 181.:
Ilyen hatszög nem nagyon van, hiszen ha egy 2 egység hosszú oldalt a kör x-re és 2-x-re bont, akkor az az x melletti 4 egység hosszú oldalt x-re és 4-x-re bontja, hiszen a körhöz külső pontból húzott érintő szakaszok egyenlőek, illetve továbblépve a 4-x melletti 2 egység hosszú oldalra, azt a körnek 4-x és 2-(4-x)-re kell bontania, szintén az érintő szakaszok miatt, azonban 2-(4-x)=x-2, csak akkor pozitív, ha x nagyobb, mint kettő, x azonban nem lehet nagyobb kettőnél, mert akkora szakaszt metszett le a kör egy másik két egység hosszú oldalból, tehát ha a beírt kör nem mehet át csúcson(azaz azt a sokszög teljes egészében tartalmazza), akkor nincs ilyen hatszög.
182:
20 3-as maradéka 1, 21-é 2, és belátható, hogy innentől kezdve periodikus, hiszen a 2 kétszerese mindig 4, aminek a 3-as maradéka mindig egy, az 1 kétszerese pedig mindig 2, aminek a 3-as maradéka kettő, ezzel a ciklus végére értünk. Látható tehát, hogy minden páratlan kitevő esetén 2 a hármas maradék. A 2333+2555-1 esetében a két kettő hatvány kitevője páratlan, hármas maradékuk 2 és 2, ezek összege 4, mínusz egy az 3, tehát az összeg osztható 3-mal, és mivel nagyobb nyilván, mint három, így nem lehet prím.
183:
Sok számolgatással(amit most nem szeretnék leírni, mert úgyis félreírnám) megkapjuk, hogy szabályos tetraédernél:
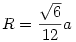
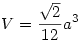

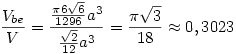
184:
Ha összekötjük a négy alsó gömb középpontját a vele szomszédosokkal, valamint az alsó 4-ét a felsőjével, akkor egy négyzet alapú gúlát kapunk, aminek minden oldala R.(ezt be lehet látni, hiszen érintik egymást) Ennek a gúlának a magassága 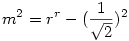 (Pitagoras tétel alapján) (Pitagoras tétel alapján)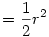 Ebből Ebből  Amiből ha meg akarjuk kapni a földtől való tárvolságot, akkor még hozzá kell adni Amiből ha meg akarjuk kapni a földtől való tárvolságot, akkor még hozzá kell adni 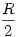 , hiszen a gúla ilyen magasan van, ekkor tehát az 5. gömb távolsága a talajtól: , hiszen a gúla ilyen magasan van, ekkor tehát az 5. gömb távolsága a talajtól:

És azt hiszem, ennyi feladat volt. Bocsánat, hogy 1, nincs ábra 2, nincs túl sok számolás leírva 3, ha valahol számolási hibát vétettem , de késő van már.
Üdv:
Yegreg
|
|
| [1008] xviktor | 2005-08-12 16:41:51 |
 Mostanaban hallottam par jo kis feladatot, gondoltam beirok ide parat.
181. feladat: Van egy hatszog mely oldalai: 2,4,2,4,2,4 /ebben a sorrendben/. Mekkora a hatszog terulete, ha tudjuk, hogy kor irhato bele?
182. feladat: Kicsit maskepp irom be ide mint az eredeti feladatban szerepel, hogy szamologepet ne lehessen hasznalni: Bizonyitsuk be hogy 2333+2555-1 nem prim!
183. feladat: Van egy szabalyos tetraederunk. A tetraederbe irt gomb terfogata hany szazaleka a tetraeder terfogatanak?
184. feladat: Van negy ugyanakkora sugaru gomb, melyek egy vizszintes asztalon paronkent erintik egymast. Pontosan kozepre "felrakunk" egy 5., a lentiekkel megegyezo sugaru gombot. Milyen messze van a fenti gomb kozeppontja a talajtol?
Jo gondolkodast!
|
|
|
|
|
| [1003] xviktor | 2005-08-08 18:23:15 |
 Az egesz levezetese sztem:
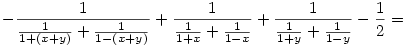
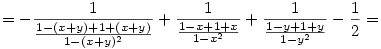
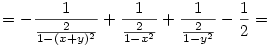
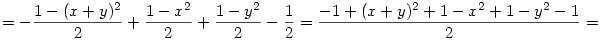
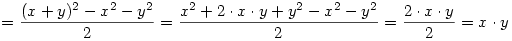
Amennyiben elirtam valamit legyszives szoljatok.
Udv: Viktor
u.i.: megtalaltam a szorzas jelet :)
|
|
|
| [1002] xviktor | 2005-08-08 17:12:05 |
 Az x2 fuggvenyt a kovetkezokepp lehet megcsinalni szerintem:
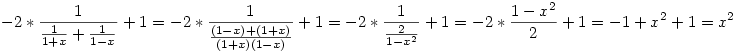 . .
Miutan megvan x2 Jonas modszerevel megvan x*y fuggveny is.
Udv: Viktor
u.i.: Legyszives segitsetek, hogy szorzas jelet hogy lehet beirni TeXben? Elore is koszi.
|
| Előzmény: [1001] rizsesz, 2005-08-08 16:28:41 |
|
| [1001] rizsesz | 2005-08-08 16:28:41 |
 Tyű, köszönöm :) a négyzet viszont számomra elérhetetlennek tűnik a páratlan kitevők miatt :( Engem is az gátolt meg eddig, és közeledek. :) segítsééééég!
|
|
| [1000] jonas | 2005-08-08 15:35:15 |
 Ezt a feladatot már hallottam, de nem tudom a teljes megoldást.
A segítség az volt hozzá, hogy állítsuk elő a négyzetre emelést először. Ha az már megvan, akkor 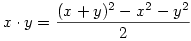 ; ahol kettővel osztani tudunk, mert ; ahol kettővel osztani tudunk, mert 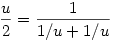
Most azt kéne megpróbálni, hogyan lehet x2-et előállítani. Eddig nem tudom, hogyan lehet, de még gondolkodom rajta.
Valami olyasmit kell használni, hogy 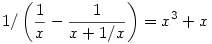 ... ...
|
| Előzmény: [989] rizsesz, 2005-08-06 21:42:56 |
|
|
| [998] rizsesz | 2005-08-07 16:46:03 |
 (elnézést, zárójelezgetni is lehet). tehát mondjuk előállítható az 1/(x+y) kifejezés, x-2y, stb, míg azonban n*m esetén nem jó az m+m+m+m...+m (n-szer) (n és m valós szám). tehát összegezve valami olyasmi a feladat, hogy lehetséges-e két számot összeszorozni csak a +, - és 1/x műveletek segíségével úgy, hogy bármely két szám esetén mindig ugyanazokat a műveleteket hajtjuk végre (mintha egy képletbe helyettesítenénk be) függetlenül a két számtól.
|
|
| [997] Yegreg | 2005-08-07 16:07:05 |
 Tehát egy olyan polinomra gondolsz, ahol x és y csak 1 és -1 hatványon lehet, és az együttható is csak 1 vagy -1 lehet mindenhol? Valamint a tagok száma véges, és nem változóval kifejezhető?
Érdekes feladat így.
Üdv
Yegreg
|
|
|
|
|
|
|
|
| [990] Yegreg | 2005-08-06 22:41:45 |
 Kedves Péter!
Kössz a címet, de én jobban megértem a saját gondolatmenetem alapján. Az már kiderült számomra, hogy az n dimenziós általánosítás helyes, mert megkérdeztem valakitől, és az mondta, hogy összegezni kell váltott előjellel a különböző dimenziós felületek számát -1-től n-ig(n dimenzióban), és 0 kapunk.(negatívval kezdjük)., Valamint, hogy a -1 dimenziós felületek száma mindig 1, és az n dimenziósé is.
És ha megnézzük, akkor ez pontosan ugyanaz, mint az enyém, egy kis átalakítás után.
Szóval, örülök, hogy rájöttem, és szeretném bizonyítani az én gondolatmenetem, legfeljebb majd utána elolvasok más gondolatmeneteket és bizonyításokat is.
Bár a nem egyszereű poliéderekre vonatkozó általánosítás helyességéről még nem kaptam visszajelzést(igaz, azt a részt magam is bizonyítottam, csak ide nem írtam le), de eddig minden egyes esetben helyes eredményt adott, bár megjegyezték, hogy néha talán nehezen használható. Valójában nem annyira, szerintem, de ez további gondolkodásra késztetett.
ScarMan barátom említette, hogy ismer egy c+l=e+2-2*k képletet, k lyukú tórusszal ekvivalens alakzatokra, ami nyilván adott esetben könnyebben használható, mint az enyém, ezekután gondoltam arra, hogy talán a speciális tulajdonságokat(ami jelen esetben a tórusz-ekvivalencia) beírva a képletbe, megkaphatjuk a speciális formulát.
Az ötlet helyesnek bizonyult, a tóruszoknál legalábbis biztosan. Ha a legvégsőként beírt képletet nézitek... Az egyszerű poliéderek száma, melyekre felbontjuk a tóruszt k. Jelen esetben k=1(ez most nem a lyukak száma, csak a képletben volt így), méghozzá egy véges henger, ha úgy tetszik gömb, amire a "standard" Euler tétel vonatkozik. A tóruszt minden lyukánál található gyűrűben "elvágjuk", így nyilván gömbbel ekvivalens alakzatot kapunk, az egyszerű poliéder pedig önmagával érintkezett akárhány csúcson és ugyanannyi élen, ezek a képletben kiejtik egymást, valamint minden egyes lyuk körüli gyűrűben pontosan két lapon(a vágás mentén, ha úgy tetszik), és mivel k(visszatérva ScarMan képletéhez, bocs, hogy a k-t két dologra használtam) lyukú tóruszról volt szó, így egy 2*k a bal oldalon, ezt ha átvisszük a jobb oldalra, akkor látható, hogy a barátom által említett c+l=e+2-2*k képletet kapjuk, tehát az általam felírt képlet alkalmas speciális esetekre vonatkozó egyenletek levezetésére.
Tulajdonképpen, feltehetőleg ekvivalens a Péter által írt címen található képlettel, csak ahhoz jobban meg kellene nézni.
Igazából azért írtam le a képletet, mert a gondolatmenetem bizonyítására vártam ötleteket, nem azért, hogy leírjátok az általános Euler tételt, mert ez már az. Csak esetleg más alakban, mint ismeritek.
Ha bizonyításként az választjátok, hogy leírjátok a ti képletetek levezetését, és belátjátok, hogy az ekvivalens az enyémmel, az elfogadható, bár mint már mondtam, nekem most nem ez lenne a célom, pontosan ezért nem néztem meg könyvben sem, mert hajlamos lennék én is így letudni, ahelyett, hogy a saját gondolatmenetemet bizonyítanám.
Üdv
Yegreg
|
|
| [989] rizsesz | 2005-08-06 21:42:56 |
 Sziasztok, egy elég meglepő probléma ütött szöget a fejembe: elő kellene állítani az f(x;y)=x*y függvényt az összeadás, kivonás és reciprok műveletek segítségével, de természetesen nem jó az x szerepeljen y alkalommal :) szóval valahogy elő kellene állítani x*y-t :)
|
|
| [988] Maga Péter | 2005-08-06 17:43:29 |
 Kedves Yegreg!
Az n-dimenziós Euler-formulát megtalálod a következő helyen minden érdekességgel: www.cs.elte.hu/~mg, ez Moussong Gábor tanár úr (ELTE, geometria tanszék) honlapja. Ezen a helyen a Konvex halmazok és politópok affin térben című, pdf kiterjesztésű állomány vége, a 6.10-6.12 pontok tartalmazzák ezt. A bizonyításhoz sajnos kell némi előismeret, főként lineáris algebra.
Minden jót!
Maga Péter
|
| Előzmény: [984] Yegreg, 2005-07-31 18:30:01 |
|
| [987] Yegreg | 2005-08-01 00:58:20 |
 Na jó, most kérek elnézést, hogy iszonyat sok hozzászólásom volt egymás után, de az eredeti képletet, amit írtam, már végiggondoltam, a nem egyszerű polinomos kiegészítést pedig általában írás közben találtam ki, és ezért több hibám is volt benne, most leírom az utolsó javított verziót, ha pedig észreveszem, hogy rosszul írtam ismét, akkor végiggondolom rendesen. Szóval itt lenne(két előjelet rontottam):
![\sum_{i=0}^{[\frac{(n-1)}2 ]}{\big(b_{2i}+b_{kozos_{2i}}\big)}-\sum_{j=0}^{[ \frac{n}2 ]-1}{\big(b_{2j+1}+b_{kozos_{2j+1}}\big)}=2*(n-2[\frac{n}2])*k](keplet.cgi?k=D82050B71C2D455C)
Bocsánat mégegyszer...
Yegreg
|
|
| [986] Yegreg | 2005-08-01 00:45:01 |
 Nah, sikerült!
Így nézne ki
![\sum_{i=0}^{[\frac{(n-1)}2 ]}{\big(b_{2i}-b_{kozos_{2i}}\big)}-\sum_{j=0}^{[ \frac{n}2 ]-1}{\big(b_{2j+1}-b_{kozos_{2j+1}}\big)}=2*(n-2[\frac{n}2])*k](keplet.cgi?k=5D108C04ECE8A701)
Az egészen általános képlet, ahol k már nem az izolált részek száma, hanem a poliédert alkotó egyszerű poliéderek száma, bkozosx pedig a poliéderen(vagy poliéderben) található olyan összes x-brán száma, amely nem csak egy egyszerű polinomhoz tartozik. (azért kozos, mert a közös-t nem szerette a TeX...).
Szóval így nézne ki egészen általánosan...
Na, a feladat még mindig a régi...
Üdv:
Yegreg
|
|
| [985] Yegreg | 2005-08-01 00:31:51 |
 Na jó, a k-t felejtsétek el(illetve ne felejtsétek, csak ne úgy jegyezzétek meg, ahogy írtam, mert az úgy nem jó), mert ha csak úgy hajítom bele a k-t, akkor nem törődnék azzal, hogy lesznek közös lapok(pontosabban n-1-bránok), vagyis kiesnek páran. Tulajdonképpen most jut eszembe, hogy nem is kell elfelejtenetek a k-t, csak jobb oldalt ki kell egészíteni, méghozzá egy ilyesmivel:
...-k*bkn-1átl.
És ezúttal megjegyezném, hogy ScarMan ismét tévedett, de azért kössz, hogy szólt azzal kapcsolatban, hogy én is tévedtem.
Jah és némi magyarázat a jobb oldal kiegészítéséhez: ki kellett vonni a közös n-1 bránok számát. Nah, és ezután most jut eszembe, hogy nem csak ilyen nem egyszerű polinom lehet. ŐŐŐŐ....kérnék lyan 5 percet, és utána beírom a rendes általános képletet nem egyszerű polinomokkal is, vagy akit az nem érdekel, az maradjon a
![\sum_{i=0}^{[\frac{(n-1)}2 ]}{b_{2i}}- \sum_{j=0}^{[ \frac{n}2 ]-1}{b_{2j+1}}=2*(n-2[\frac{n}2])](keplet.cgi?k=3EFD1E39D4438431)
képletnél egyszerű polinomok esetén. Nemsokára újra jelentkezem. Üdv:
Yegreg
|
|
| [984] Yegreg | 2005-07-31 18:30:01 |
 Pár napja írt egy e-mailt egy barátom(az fórumon ScarMan néven), írta, hogy emlékszem-e még, amikor az Euler tétel n-dimenziós általánosításáról beszéltünk, valamint elküldte az egyik ötletét. Aztután a másnap délelőttöt azzal töltöttem, hogy gondolkoztam, majd arra jutottam, hogy helytelen az egyenlete, és kitaláltam egy egyenletet, ami feltehetőleg helyes. Íme: ![\sum_{i=0}^{[\frac{(n-1)}2 ]}{b_{2i}}-
\sum_{j=0}^{[ \frac{n}2 ]-1}{b_{2j+1}}=2*(n-2[\frac{n}2])*k](keplet.cgi?k=B06847CB32B1ED8E)
Ahol n a dimenziók száma, bx az n dimenziós test x-bránjainak(x dimenziós felületeinek, azaz x=0-nál csúcs, x=1-nél él, x=2-nél lap, x=3-nál test stb.) száma, k pedig az izolált és összefüggő részek száma(ez csak akkor szükséges, ha nem egyszerű a polinom). A képletet az alapján kaptam meg, hogy kiindultam abból, hogy egy n-1 dimenziós testre igaznak kell lennie az n dimenziós Euler tételnek, ha figyelembe vesszük azt, hogy az n-1 dimenziós testnek pontosan 2 db n-1-bránja van, de ez logikus, hiszen két oldala van. A képletet úgy kapjuk meg, ha feltételezzük, hogy ez az állítás megfordítva is igaz.
Az ok, ami miatt többek között beírom ezt ide az, hogy a képlet megkapása utáni 2-3 napban nem sikerült bizonyítanom, hogy a fenti állítás megfordítottja igaz, a feladat tehát az lenne, hogy igazoljuk a képlet helyességét, vagy cáfoljuk meg azt.
Sok sikert!
Üdv:
Yegreg
|
|
| [983] Yegreg | 2005-07-30 19:14:02 |
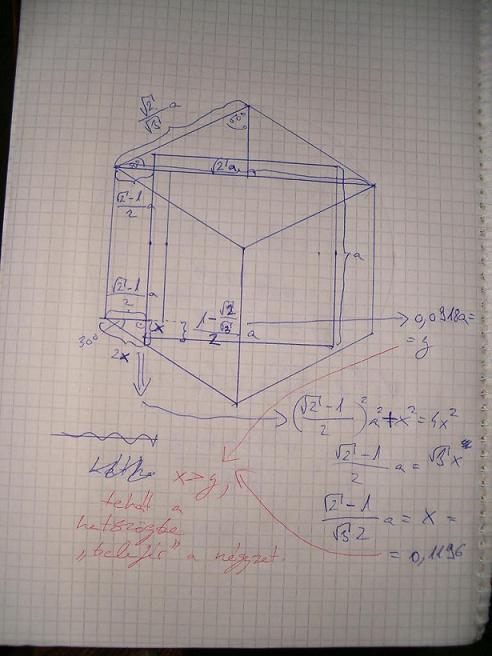
 A kockás feladat megoldása: Legyen a kocka éle a! ha úgy forgatjuk a kockát, hogy egy szabályos hatszöget lássunk(azért forgatjuk így, mert a testátlóval párhuzamosan akarjuk keresztükfúrni), akkor a hatszög oldalai nyilván nem a hosszúságúak lesznek, mondjuk a perspektívikus torzulás miatt, de hívhatjuk máshogy is. Meg kell tehát kapnunk a hatszög oldalait, ehhez kell egy ismert érték, ami pedig egy olyan szakasz, ami egy olyan nézetből, ahol valahány oldal valóban a, a forgatás egyenesével párhuzamos. Ilyen lehet egy olyan nézet, ahol csak a kocka egyik oldalát, azaz egy négyzetet látunk, ilyenkor a négyzet oldalai nyilván a hosszúságúak. A négyzet nézetből két felső csúcsa(azaz a lapátló) körül megfelelően forgatva a hatszögnézetet kapjuk, és mivel a lapátló körül forgattunk, annak hossza változatlan, azaz gyök 2*a. Innentől a számításokat az ábrán láthatjátok (sajnos nincs olyan kafa programom, mint LoryTibinek, de van kafa füzetem és kafán tudok béna ábrákat csinálni, de remélem azért látható minden). A számítások végén megkapjuk, hogy a hatszögbe írható az a oldalú négyzet, azaz így kifúrva átfér rajta a másik kocka. Az, hogy a kifúrt test egybefüggő még be kell látni, pl. ha egy gráfként ábrázoljuk az új testet, akkor látjuk, hogy az eredeti kocka két csúcsát és hat élének egyrészét hagytuk el, valamint az is láthatjuk, hogy a kocka megmaradt hat csúcsának és a fúrás során létrejött másik hat csúcsok bármelyikét köti őssze él másik csúccsal és nincsen izolált rész, valamint a számolásokból kiderül, hogy a fúrás után is az élekhez pozitív térfogat tartozik, azaz tulajdonképpen nem tűnt el él, csak részük. Azért az is igaz, hogy ténylég éppen, hogy befér, hiszen egy 1m*1m*1m-es kockánál csak 1,39 cm-en "múlik".
Üdv:
Yegreg
|
 |
|
| [982] lorantfy | 2005-07-28 11:30:00 |
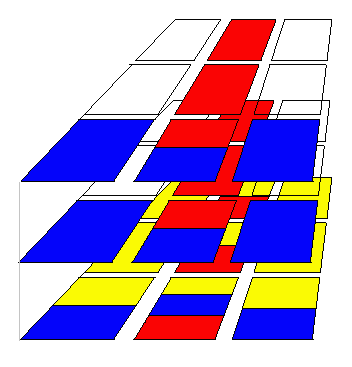
 Atosz 178. feladata ennek a 3 D-s változata. A 3 egymásutáni kirakás és választás után azt tudjuk meg, hogy a gondolt lap pl. a sárga szinten, a piros oszlopban és a kék sorban van. A 3 információ egyértelműen megadja a gondolt lapot és persze ezekből a gondolt lap szorszáma is kiszámolható az utolsó összegyűjtéskor kapott pakliban.
A kirakás módja garantálja, hogy először pl. az azonos szinteken lévő kártyák vannak azonos kupacban, majd az azonos oszlopokban, majd az azonos sorokban lévő 9-9-9 lap kerül azonos kupacba.
|
 |
| Előzmény: [981] lorantfy, 2005-07-28 11:14:20 |
|
| [981] lorantfy | 2005-07-28 11:14:20 |
 Kedves Atosz, Károly, Viktor és Érdeklődők!
Nagyon jó az Atosz által [966]-ban feladott kártyás feladat. Legyen a 178. feladat.
Gyerekkoromban mi is csináltuk ennek a 2 dimes változatát. 9 db kártyát kiraktunk 3x3-as alakzatba és Béla gondolt egy lapra megmondta melyik oszlopban van.
Most összeszedjük a kártyákat oszloponként, lesz 3 kupac, ezeket egymásra helyezzük. Megfordítjuk a csomagot és újra kirakjuk soronként. Béla most is megmondja melyik oszlopban van a kártya és már tudjuk is melyik lapra gondolt Béla.
Na most, ha az elején, miután kiraktuk a 3x3-as alakzatot, azt kérjük Bélától: Gondoljon egy kártyára és mondja meg melyik sorban és melyik oszlopban van és ezután mi kitaláljuk melyik a gondolt lap, Béla köröhög minket!
Pedig valójában pontosan ez történik. Igaz Bélának mindkétszer oszlopszámot kell mondania, de a kártyák beszedése és újra kirakása miatt, gyakorlatilag ugyanaz történik.
Az ábrán a szemléltetés kedvéért direkt kiválogattam a kártyákat. Tfh. Béla a piros királyt választja. Tehát először a 2. oszlopot mondja - ebből tudjuk, hogy királyról van szó. Az összeszedés és újra kirakás után a 3. oszlopot mondja - ebből tudjuk, hogy piros szinű kártyáról van szó.
A lényeg az, hogy bár mindkétszer oszlopszámot mondott Béla, az újrakirakás miatt ez két független koordináta és ebből egyértelműen megadható a gondolt lap.
|
 |
| Előzmény: [980] xviktor, 2005-07-21 14:40:39 |
|
|
|
| [978] lorytibi | 2005-07-20 17:37:37 |
 Hát igen, ha egy ilyet hall az ember, ami teljesen lehetetlennek tűnik, rögtön tudja, hogy meg lehet csinálni! Segítségemre volt a tesóm, aki egy gyönyörű animációt csinált erre nekem. Ebből nagyon szépen látszik, hogy meg lehet csinálni ... Sajnos azt nem tudom feltenni, csak egy képet belőle. Lényeg, hogy a a kockát a testátlónál furjuk át, és így pont átfér egy ugyanakkora kocka (Az ábrán a kékes kockát furtam át, és a zöldet dugom át rajta)
|
 |
|
|
| [976] Atosz | 2005-07-20 12:09:48 |
 Közben eszembe jutott egy újabb érdekes feladat!
Át lehet-e fúrni egy tömör fakockát úgy, hogy egy másik ugyanolyan méretűt egyben átdugjunk a lyukon?
|
|
| [975] Atosz | 2005-07-20 11:53:55 |
 Kedves Viktor!
Ez a megoldásod jó, de így tényleg fejben kell tartani kilenc kártyalapot, ami nem könnyű! A hármas számrendszer könnyebb, az megy csukott szemmel is csak azt kell hallani, hogy hová kerül a jelzett csomag. Minden jót!
|
| Előzmény: [973] xviktor, 2005-07-20 09:19:32 |
|
| [974] Atosz | 2005-07-20 11:50:12 |
 Szia Onogur, és mindenki!
Tökéletes a megoldásod, gratulálok! Pontosítva úgy működik, hogy ha a kiválasztott csomag felülre kerül akkor 0, ha középre, akkor 1, ha alulra akkor pedig 2 lesz a megjegyzett érték. Ezt megcsinálva háromszor egymás után, akkor kapunk egy hármas számrendszerbeli számot, amit visszafelé olvasva konvertálunk át (azaz az első összerakás kódja adja az egyes helyiértéket, míg az utolsóé a kilencest) tizesbe, ami adja a kártya helyét. Elég hatásos!
Más! Tartozom még nektek Onogur régebbi karikás feladatának általánosításával, azaz hogyan lehet tetszőleges sok karikát összefűzni úgy, hogy egyben marad (csak vágással jönne szét) ám bármelyiket felvágva minden karika leszedhető lesz. (Lásd a fotón!) Ha esetleg nem látszana jól, akkor nagyjából leírva: Az elsőn átbújtatjuk a másodikat, két végét lehajtjuk, majd azon a két fülön a harmadikat, annak is lehajtjuk a végeit, stb... majd az n-iket egy normál karikával lezárjuk.
ui: (Onogurnak) Könyv!
|
 |
| Előzmény: [971] Hajba Károly, 2005-07-20 08:29:41 |
|
| [973] xviktor | 2005-07-20 09:19:32 |
 Lenne egy megoldasom, ami egyedul a "csukott szemnek" mond ellent, de kivancsi lennek a velemenyekre:
A 27 kartya 3 pakliba kerul. Egyikre ramutatunk igy mar csak 9 kartya lehet jo. A kovetkezo osztasnal a 9 kartya 3as csoportokban kulon kerul /3-3-3/, igy a masodik ramutatas utan mar csak 3 kartya lehet a jo. Az utolso osztasnal a maradek 3 kartya is kulon-kulon kerul, igy a vegen mar konkretan tudni fogjuk melyik a valasztott kartya.
Egyben lenne egy masik feladatom. Attila feladatat nem olvastam el rendesen, es azt hittem Gergonne rakja tetszolegesen egymasra a paklikat. Ha igy lett volna, hogyan tudta volna mindenfele szamolgatas nelkul megmondani melyik lap a keresett /ezt mar lehet csukott szemmel is csinalni/.
Udv: Viktor
|
| Előzmény: [972] xviktor, 2005-07-20 08:38:45 |
|
|
| [971] Hajba Károly | 2005-07-20 08:29:41 |
 A trükk matematikai alapja a következő lehet:
32-5=27=33
Minden kirakásnál megfigyeli hogy az a hármas hova kerül és ebből lehet kiszámolni. Egy hármas számrendszerbeli szám jön ki, amit fejben átkonvertál 10-esre és megvan a kártya helye. A részleteket még ki kell dolgozni, de ez az alapelv.
O.
|
| Előzmény: [965] Atosz, 2005-07-19 19:44:48 |
|
| [970] Atosz | 2005-07-20 07:54:08 |
 Sziasztok!
Mindenkivel megosztom Viktornak írt gondolataimat, nehogy mások is tévútra menjenek. Természetesen matekfeladatról van szó, amit Gergonne gondolt ki, de nem túl nehéz, ám érdekes. A bűvész tulajdonképpen csukott szemmel is dolgozhat, nem kell látnia, hogy melyik lap hova kerül és a néző (a lap gondolója) szedi össze mindhárom esetben a kiskupacokat, tehát a jelzett kiskupac bárhová kerülhet, azaz felülre, középre, alulra. Minden jót!
|
|
| [969] xviktor | 2005-07-19 22:50:14 |
 Ujabb otletem tamadt. Azt is elkuldtem e-mailben.
|
|
|
|
|
| [965] Atosz | 2005-07-19 19:44:48 |
 Sziasztok!
J.D.Gergonne francia matematikus kártyatrükkje volt a következő feladvány:
A 32-lapos kártyacsomagból (pl. magyarkártya) kiveszünk 4 hetest és egy nyolcast, majd a néző a maradékokból rágondol egy lapra. Ezután a jól megkevert csomagot szinével felfelé balról jobbra, egyesével három kupacba kirakjuk (bal, közép, jobb, bal, közép, jobb, stb...). A néző megmutatja nekünk, hogy melyik kupacban van a gondolt lap, majd tetszőleges sorrendben egymásra helyezi a kupacokat. A paklit megfordítjuk (így a szine lesz lefelé), majd egyesével újra kezdjük a kirakást (természetesen megint minden lerakott lapot szinével felfelé teszünk az asztalra, hogy lássa őket). Ezt az egész kirakás, megmutattatás, összeszedés dolgot összesen háromszor megcsináljuk, majd az egész paklit sorba kiterítjük és megmutatjuk a gondolt kártyát.
Kérdés, hogy mi a trükk? (Természetesen matematikai feladványról van szó!)
Minden jót, Atosz!
|
|
| [962] 2501 | 2005-06-14 11:12:21 |
 Nem csak az N, Z, Q, R, stb. számhalmazok, hanem ezek részhalmazai is (pl. a páros számok halmaza).
Ezt felhasználva egy lehetséges megoldás:
a 3-mal osztva
A: 0 vagy 1
B: 1 vagy 2
C: 2 vagy 0
maradékot adó számok halmazai.
|
| Előzmény: [961] Kérdező, 2005-06-14 10:19:25 |
|
| [961] Kérdező | 2005-06-14 10:19:25 |
 A példám egyszerű, de mégsem ugrik be a megoldás. Kérlek segítsetek!
----Halmazelmélet----
Adott 3 számhalmaz, melyekben külön-külön végtelen sok elem van. Egy-egy halmaz metszetében szintén végtelen sok elem található. Viszont a közös metszetben nulla, az ugyanis üres!
Hogy lehetséges ez? Tudomásom szerint ugyanis a számhalmazok egymás elemei...
R > Q > Z > N
Tehát két ilyen számhalmaz metszetét mindig a kisebbik halmaz elemei jelentik. Nem értem, hogy a közös metszet hogy lehet üres!?
Előre is köszi a segítséget!
|
|
| [960] jonas | 2005-06-13 21:51:02 |
 A g(x)=x+1 is jó ellenpélda mindhárom esetre. A g(x)=1-et én is kipróbáltam, de úgy látszik, nem vettem észre, hogy az is mindig jó. Szerintem ez bizonyítja, hogy én nem számoltam túl sokat, hiszen csak beírtam az első olyan ellenpéldát, ami kijött.
|
| Előzmény: [959] Lóczi Lajos, 2005-06-13 14:45:33 |
|
| [959] Lóczi Lajos | 2005-06-13 14:45:33 |
 Hogy hogy tudtok ilyen bonyolult ellenpéldákat kifundálni :-), g(x)=x+1, egy csomót kell számolni, hogy leellenőrizze az ember.
(Ami nekem -- igaz, sajnos nem öt perc után -- beugrott, mint ellenpélda, az a szimpla g(x):=c választás: ez alkalmas c-vel mindegyiket cáfolja. Szinte érzem, hogy sugallják a feladat kitűzői, hogy próbáljuk meg a cx alakú függvényeket, mint "jobb szélső" esetet, 0 és 1 közötti c-vel, ezekre azonban mindhárom eset teljesül...)
|
| Előzmény: [958] jonas, 2005-06-12 18:54:39 |
|
| [958] jonas | 2005-06-12 18:54:39 |
 Nem baj, ha lelövöm a megoldást?
Ha g(x)=1, akkor 0= g'(x) így a feltétel teljesül, de g'(x) így a feltétel teljesül, de 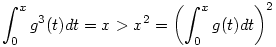 ha 0<x<1, tehát (a) vagy (c) biztosan nem mindig igaz. ha 0<x<1, tehát (a) vagy (c) biztosan nem mindig igaz.
Másrészt a (b) sem feltétlenül igaz, szerintem g(x)=x+1 ellenpélda rá.
|
| Előzmény: [957] Lóczi Lajos, 2005-06-12 14:09:43 |
|
| [957] Lóczi Lajos | 2005-06-12 14:09:43 |
 177. feladat. Nemrég valahol tesztkérdésként (!) tűztek ki egy, az alábbihoz hasonló feladatot (tehát úgy gondolom, nem volt túl sok idő a megoldására).
Válasszuk meg a g:(0, ) ) R deriválható függvényt tetszőlegesen úgy, hogy 0 R deriválható függvényt tetszőlegesen úgy, hogy 0 g'(x) g'(x) 1 teljesüljön minden x>0 esetén. Döntsük el, melyik állítás igaz mindig. 1 teljesüljön minden x>0 esetén. Döntsük el, melyik állítás igaz mindig.
a.) Minden x (0,1) (0,1)
b.) Minden x 1 1
c.) Minden x>0
esetén fennáll, hogy
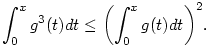
|
|
| [956] Lóczi Lajos | 2005-06-12 13:45:31 |
 Szép megoldás. Beírom, hogy a feladatra milyen "megoldást" láttam, tanulságos a kettőt összehasonlítani. (Idézőjelbe tettem azokat a részeket, ami miatt a két megoldás látszólagosan elétér.)
Alkalmazzuk a jobb oldalon a tangensfüggvény ismert "azonosságát",
és a rövidség kedvéért pl. legyen y:=tg(x), valamint a:=tg(1) ekkor azt kapjuk, hogy
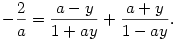
Ez utóbbi egyenletnek azonban y-ban nincs megoldása, "tehát" a kiindulási egyenletnek sincs.
|
| Előzmény: [955] levi, 2005-06-10 20:15:33 |
|
| [955] levi | 2005-06-10 20:15:33 |
 -2ctg1=tg(1-x)+tg(1+x)
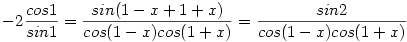
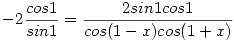
-cos(1-x)cos(1+x)=sin21
-(cos1cosx+sin1sinx)(cos1cosx-sin1sinx)=sin21
sin21sin2x-cos21cos2x=sin21
sin21sin2x-(1-sin21)(1-sin2x)=sin21
sin21sin2x-(1-sin2x-sin21+sin21sin2x)=sin21
-1+sin2x=0
sin2x=1
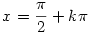
+ellenörzés (remélem nem baj hogy azt nem írom ide)...
|
| Előzmény: [954] Lóczi Lajos, 2005-06-09 14:30:46 |
|
| [954] Lóczi Lajos | 2005-06-09 14:30:46 |
 176. feladat. Oldjuk meg a valós számok halmazán az alábbi egyenletet:
-2ctg1=tg(1-x)+tg(1+x)
|
|
|
| [952] jonas | 2005-06-05 20:39:58 |
 Megpróbálom.
Tegyük fel, hogy az f folytonos függvény az egész R-en értelmezett, és minden értéket pontosan kétszer vesz fel.
Vegye fel az y0 számot az x0 és x1 pontokban, ahol x0<x1. Tekintsük az (x0,x1) intervallumot! Mivel itt f nem veszi fel x0-t, vagy csak y0-nál nagyobb, vagy csak y0-nál kisebb értéket vesz fel. Szimmetriaokokból tegyük fel, hogy csupa nagyobbat vesz fel. Ezen a középső intervallumon a függvénynek van maximuma, mégpedig az x2 pontban, ahol f(x2)=y2.
Legyen y3 a másik pont, ahol f(y3)=x2. A szimmetria miatt feltehetjük, hogy y2<y3
Két eset lehetséges.
Vagy x2<x3<x1, de ekkor az (y2,y3) intervallumban f értéke kisebb y2-nél, de nagyobb y0-nál. De az ilyen értékeket f a közbülsőérték-tétel miatt az (y0,y2) és az (y3,y1) intervallumon is mind felveszi, tehát legalább három helyen is, ami ellentmondás.
Ha viszont x1<x3, akkor f az (y0,y2), (y2,y1) és az (y1,y3) intervallumon is felveszi az összes (x2,x3)-beli értéket, ami lehetetlen.
|
| Előzmény: [951] Lóczi Lajos, 2005-06-05 19:29:33 |
|
|
|
| [949] Lóczi Lajos | 2005-06-04 15:56:10 |
 Igen, igazad van, a [946]-ban kétszer is tévedtem: persze "-" helyett ott "+"-t akartam írni, másrészt rosszul láttam, hogy "nem igaz" -- szerintem is jó a képlet, amit írtál.
|
| Előzmény: [948] 2501, 2005-06-03 19:49:31 |
|
| [948] 2501 | 2005-06-03 19:49:31 |
 Megpróbálom indokolni, hogy
![f_n(x) \quad = \quad \left[\frac x n\right]+x-[x]](keplet.cgi?k=DA10EEB0EC3F69C7)
(ahol ![\left[x\right]](keplet.cgi?k=DAA57752EF9A484F) az alsó egészrész) szerintem miért működik. Bontsuk fel két függvény összegére: az alsó egészrész) szerintem miért működik. Bontsuk fel két függvény összegére:
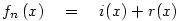
![i\left(x\right) \quad = \quad \left[\frac x n\right]](keplet.cgi?k=A7FADA218258A5C7)
![r\left(x\right) \quad = \quad x-\left[x\right]](keplet.cgi?k=3C012AAE469F98BB)
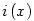 grafikonja egy n hosszúságú "fokokból" álló, növekedő "lépcső", melyben a "fokok" az egészeknél kezdődnek. grafikonja egy n hosszúságú "fokokból" álló, növekedő "lépcső", melyben a "fokok" az egészeknél kezdődnek. 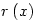 tulajdonképpen x törtrésze (írhattam volna tulajdonképpen x törtrésze (írhattam volna 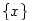 -et is), tehát a grafikonja negyvenöt fokos, és 1 magas "sörtékből" áll. A kettő összegének grafikonján a "sörték" rákerülnek a "lépcsőfokokra", és minden fokon éppen n darab lesz. -et is), tehát a grafikonja negyvenöt fokos, és 1 magas "sörtékből" áll. A kettő összegének grafikonján a "sörték" rákerülnek a "lépcsőfokokra", és minden fokon éppen n darab lesz.
|
| Előzmény: [944] 2501, 2005-06-02 21:51:06 |
|
|
| [946] Lóczi Lajos | 2005-06-03 16:48:28 |
 175. feladat. Adjunk meg olyan folytonos valós függvényt, amelynek értelmezési tartománya az egész számegyenes és minden értéket pontosan kétszer vesz fel.
|
|
| [945] Lóczi Lajos | 2005-06-03 16:45:44 |
 (A kérdőjeles egyenlőség nem igaz.)
Másrészt nem is működnek jól a képletek, pl. a bal oldali esetén (ha [.] jelöli az alsó egészrészt (=floor)), akkor pl. ![x-[x]-[\frac{x}{2}]](keplet.cgi?k=5F969C09B1B31D18) a felet 3-szor veszi fel, de az egész értékeket csak kétszer. a felet 3-szor veszi fel, de az egész értékeket csak kétszer.
|
| Előzmény: [944] 2501, 2005-06-02 21:51:06 |
|
| [944] 2501 | 2005-06-02 21:51:06 |
 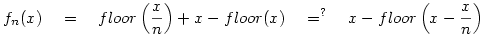
Aggodalomra semmi ok, mára befejeztem.
|
|
| [943] 2501 | 2005-06-02 20:57:45 |
 Megint nem jó, csak f2(x) jó. :o(
|
|
| [942] 2501 | 2005-06-02 20:43:40 |
 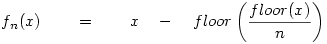
Ahol floor(x) az a legnagyobb egész szám, amely nem nagyobb x-nél. Így biztosan jó.
|
|
| [941] 2501 | 2005-06-02 19:38:23 |
 Mégsem jó, pl. f2(x) három helyen 0. :o)
|
|
| [940] 2501 | 2005-06-02 19:07:11 |
 174.
fn(x) = x - [x] mod n
Ez leírja az egész függvénycsaládot. Legalábbis most jónak tűnik. :o)
|
|
| [939] Lóczi Lajos | 2005-06-01 13:40:51 |
 174. feladat. Adjunk meg olyan valós függvényt (ha van), amelynek értelmezési tartománya is és értékkészlete is az egész R, és minden értéket pontosan
a.) kétszer
b.) háromszor
c.) négyszer
vesz fel.
|
|
| [938] Lóczi Lajos | 2005-05-18 21:12:23 |
 173. feladat. Adjuk meg az összes olyan pozitív x,y,z számot, melyekre teljesül, hogy
xy=yz=zx.
(A feladat más, mint a régebbi hasonló kinézetű társa.)
|
|
| [937] Lóczi Lajos | 2005-05-18 15:56:07 |
 A "nem létezik" helyett persze jobb "nem létezik véges"-et mondani. (Én talán annyival gondoltam egyszerűbbre, hogy f(x)=1 és 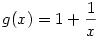 is megfelelnek ellenpéldaként a 171. feladatban.) is megfelelnek ellenpéldaként a 171. feladatban.)
Ennyi előkészítés után végre következhet a tényleges feladat.
172. feladat. Legyenek f és g olyan, az egész számegyenesen értelmezett, deriválható függvények, hogy 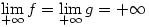 és és 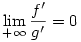 . .
Igaz-e, hogy ekkor 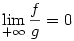 ? ?
|
| Előzmény: [936] nadorp, 2005-05-18 07:50:32 |
|
| [936] nadorp | 2005-05-18 07:50:32 |
 Úgy látszik, az analízis nem túl népszerű. Az alábbi megoldás biztos nem a legegyszerűbb, de általános.
A válasz nem, ugyanis legyen p(x)az egész számegyenesen deriválható függvény, és tegyük fel, hogy 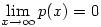 ( ilyen pld. e-x). ( ilyen pld. e-x).
Legyen f(x)=ep(x)-p(x) és g(x)=p(x). Ekkor:
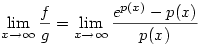 nyilván nem létezik, viszont nyilván nem létezik, viszont
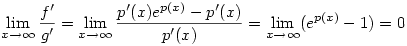
|
| Előzmény: [934] Lóczi Lajos, 2005-05-10 16:57:48 |
|
|
| [934] Lóczi Lajos | 2005-05-10 16:57:48 |
 Rendben, gondoltam, hogy ezzel semmi gond nem lesz. Akárcsak ezzel:
171. feladat. Tegyük fel, hogy 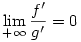 . Igaz-e, hogy ekkor . Igaz-e, hogy ekkor 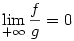 ? ?
(Ezután már csak egy variánsom lesz, ami az igazi feladat.)
|
| Előzmény: [931] nadorp, 2005-05-10 11:05:27 |
|
| [933] levi | 2005-05-10 13:52:19 |
 nem tud vki vmi olyan könyvet/bármit ami a 4,5,...dimenziós geometriával foglalkozik? elkezdett érdekelni a dolog, gondoltam itt biztos tud vki vmi ilyet ajánlani...
|
|
|
|
| [930] neo | 2005-05-10 01:07:15 |
 Http://matek2005.fw.hu
|
|
| [929] Lóczi Lajos | 2005-05-10 00:23:57 |
 Gratulálok, nekem is ezek az értékek jöttek ki (bár én sehol sem használtam geometriai meggondolásokat -- vannak példák arra, hogy az analógiáink magas dimenzióban nem működnek), úgyhogy azért a többieknek is maradhat még annyi a feladatból, hogy vagy igazoljuk a geometriai érvelésedet, vagy geometriától függetlenül oldjuk meg a problémát.
|
| Előzmény: [928] levi, 2005-05-09 23:50:42 |
|
| [928] levi | 2005-05-09 23:50:42 |
 167-170. feladatra: a két dimenziós eset vizsgálata: vegyük a két külső kör középpontját, ezek A(r+1,0) és B(0,r+1). Vegyük azt a szakaszt amit ez a két pont határoz meg, a keresett legkisebb sugarú kör érinti egymást, mégpedig a szakasz felezőpontjában, így már adott ennek is a koordinátája, a sugár egyenlő a felezőpont és az egyik külső kör középpontjának távolságával, r-re rendezés után szerintem ez: 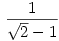 . .
Három dimenziós esetben kössük ismét össze ezeket a pontokat, ezek egy háromszöget fognak meghatározni. a keresett pont a háromszög magasságpontja. a háromszög szerencsére szabályos, így a magasságpont egybeesik a súlyponttal, a súlypont koordinátái pedig kiszámíthatóak a csúcsok koordinátáiból... ismét felírva egy középpont és a magasságpont távolságát az egyenlő lesz r-rel , és utána rendezve megkapjuk r-t, ami nálam 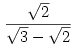
ezután az általános n dimenziós eset: sajnos nem tudok 4 vagy magasabb dimenzóban látni, és annak a (koordináta)geometriáját sem tudom, de talán az előző két esetből levont következtetésem jó lesz... szóval a körök középpontjai adottak, a keresett pont mely egyenlő távolságra van mindegyiktől szerintem K(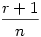 , , 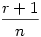 ,..., ,...,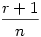 ) (összesen n-szer). Ekkor egy középpont és a K távolsága lesz egyenlő a sugárral. Mivel a középpontok mind egy-egy tengelyen vannak, ezért koordinátái közül pontosan egy lesz r+1 az összes többi 0. Ha felírjuk a távolságképletet, majd kiemelünk a gyök alól ) (összesen n-szer). Ekkor egy középpont és a K távolsága lesz egyenlő a sugárral. Mivel a középpontok mind egy-egy tengelyen vannak, ezért koordinátái közül pontosan egy lesz r+1 az összes többi 0. Ha felírjuk a távolságképletet, majd kiemelünk a gyök alól 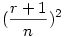 -t, akkor azt kapjuk hogy -t, akkor azt kapjuk hogy 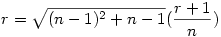 . Rendezzük r-re, majd egyszerűsítünk, akkor azt kapjuk hogy . Rendezzük r-re, majd egyszerűsítünk, akkor azt kapjuk hogy 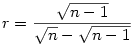 . Ezalapján az n=4 eset már könnyen kiszámolható... . Ezalapján az n=4 eset már könnyen kiszámolható...
|
|
|
|
| [925] Lóczi Lajos | 2005-05-09 21:58:25 |
 169. feladat. Tekintsük a 4 dimenziós térben az origó középpontú egységsugarú hipergömböt (azaz 4 dimenziós gömböt). A 4 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 4 darab egyforma, r sugarú hipergömböt. Legalább mekkora legyen az r>0 szám értéke, hogy legyen olyan pont, amely mind a 4 hipergömbön rajta van?
170. feladat. Általánosítsuk az előző kérdést n-dimenzióra, és adjuk is meg a minimális r>0 értéket a dimenzió függvényében.
|
|
| [924] Lóczi Lajos | 2005-05-09 21:55:48 |
 168. feladat. Tekintsük a közönséges 3 dimenziós térben az origó középpontú egységgömböt. A 3 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 3 darab egyforma, r sugarú gömböt. Legalább mekkora legyen az r>0 szám értéke, hogy legyen olyan pont, amely mind a 3 gömbön rajta van?
|
|
| [923] Lóczi Lajos | 2005-05-09 21:52:11 |
 167. feladat. Tekintsük a közönséges 2 dimenziós síkon az origó középpontú egységkört. A 2 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 2 darab egyforma, r sugarú kört. Legalább mekkora legyen az r>0 szám értéke, hogy e két külső körnek is legyen közös pontja?
|
|
|
|
|
|
|
| [917] Lóczi Lajos | 2005-05-05 23:16:27 |
 165. feladat. Legyen f az egész számegyenesen értelmezett, legalább kétszer deriválható korlátos valós függvény. Igaz-e, hogy f második deriváltjának van legalább egy valós zérushelye?
|
|
| [916] b.andi | 2005-05-05 22:47:36 |
 Jó én se szó szoros értelemben értettem a gúnyolódást ez inkább önirónia volt... Tudod azért teszem a röhögőfejeket a mondataim után, hogy azt nem kell halálosan komolyan venni...Amúgy tényleg köszi a segítséget!!!
|
| Előzmény: [914] jonas, 2005-05-05 20:37:50 |
|
| [915] Lóczi Lajos | 2005-05-05 22:42:01 |
 164. feladat. Számítsuk ki a
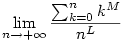
határértéket, ha M és L adott pozitív egészek.
|
|
|
| [913] b.andi | 2005-05-05 19:35:27 |
 Most kigúnyolsz? Ne máááááá..... :) mondtam hogy nem vagyok matek zseni, nekem már ez is érdekes, ha egyátalán nekifogok egy ilyen feladatnak... :) Vagy ha tudsz egy olyan topicot, hogy "Oldjatok meg gagyi feladatokat" akkor szólj :) Na mindegy amúgy nagyon nagyon köszi!!!!!! most jut eszembe nem is az volt a kérdés, hogy rajta van-e, hanem hogy mi a kör egyenlete... Nekem ez lett k:(x-3)2 + (y+4)2= 5 (vagyis négyzetgyök öt a négyzeten) (ti hogy tudtok felső indexbe írni?) és k': (x-1)2 + (y-6)2 =5 Szerintetek ez jó?
|
| Előzmény: [912] jonas, 2005-05-05 18:24:33 |
|
|
| [911] Sirpi | 2005-05-05 15:25:54 |
 Az 1. feladatot bevállalom, a többit meghagyom másoknak.
A(-2;1), B(8;1), P(0,y), ahol y az ismeretlen. Innen a PA vektor (-2; 1-y), a PB vektor (8; 1-y)
Két vektor meröleges, ha skalárszorzatuk nulla, azaz -16+(1-y)2=0, innen y=5 vagy y=-3.
|
| Előzmény: [908] b.andi, 2005-05-05 12:13:12 |
|
| [910] b.andi | 2005-05-05 15:02:07 |
 Nem adok többet ígérem!!!! :) Az előzőt rosszul csináltam mert nem a II. síknegyedbe "raktam" a pontot. Még ezenkívül a kettesbe mertem belekezdeni, végig is csináltam, de hát nem vagyok egy matek zseni... a többiről fogalmam sincs (hát a matektanárunk nem egy ász):) Egyébként ezek voltak a matek dolgozatom kérdései...
|
|
|
| [908] b.andi | 2005-05-05 12:13:12 |
 Köszi szépen!!!! Nem akarok visszélni segítőkészségeddel, de nagyon megköszönném, ha segítenél (vagy valaki más)ezekben! :)
1. Adott A(-2;1) és B(8;1). Az y tengely mely pontjaiból látszik az AB szakasz derékszög alatt?
2.Mi az egyenlete annak a körnek, melynek sugara négyzetgyök 5, és az "e": x-2y=6 egyenest A (2;4) pontjában érinti?
3. Írja fwl az (x-2)2 +(y-1)2 =5 kör y=2x egyenessel párhuzamos érintőinek egyenletét!
|
| Előzmény: [907] Fálesz Mihály, 2005-05-05 10:12:06 |
|
| [907] Fálesz Mihály | 2005-05-05 10:12:06 |
 A pont a II. síknegyedben van, a kör középpontja is ott lesz. Legyen a középpont (-a,a), a sugár a. A kör egyenlete:
(x+a)2+(y-a)2=a2.
Az egyenletnek teljesülnie kell x=-2, y=4 esetén, tehát
(-2+a)2+(4-a)2=a2
a2-12a+20=0
a=2 vagy a=10.
A két lehetséges egyenlet tehát:
(x+2)2+(y-2)2=4 és (x+10)2+(y-10)2=100.
|
| Előzmény: [906] b.andi, 2005-05-05 09:26:14 |
|
| [906] b.andi | 2005-05-05 09:26:14 |
 Hello! Megoldanátok nekem ezt a feladatot? ( csak arra vagyok kiváncsi, hogy jól dolgoztam-e): Egy kör érinti mindkét tengelyt és átmegy a P(-2;4) ponton. Mi a kör egyenlete?
|
|
| [905] Lóczi Lajos | 2005-05-04 22:34:50 |
 163. feladat. Tekintsünk egy r>0 sugarú kört egy adott perempontjához tartozó érintőegyenessel együtt. Egy teljes fordulat erejéig csúszásmentesen görgessük végig a kört az egyenesen. A kijelölt perempont eközben egy G görbét ír le. Mekkorának válasszuk r értékét, ha azt szeretnénk, hogy az egyenes és G által határolt síkidom területének és kerületének mérőszáma ugyanakkora legyen?
|
|
| [904] tudniakarok | 2005-05-04 22:18:53 |
 Na ehhez a következőt találtam:
"... július 27-ére minden adat végleges lesz ahhoz, hogy beindíthassuk a vonalhúzás számítógépes eljárását. Ez egy többszörös biztosítással lefuttatott matematikai algoritmus,mely folyamatosan összeveti az egyes intézmények és szakok irányszámait az oda jelentkezők számával és elért felvételi pontszámaival. Minden egyes szak esetében az oda jelentkezők pontszámaiból alakul ki egy sorrend,amelynek csúcsán a legtöbb pontot elért jelentkező áll, majd sorra következik a többi... a szabály az, hogy a ténylegesen felvett hallgatók száma alulról közelíti meg az irányszámot. Mindezek figyelembevételével alakul ki végül július 27-én, előreláthatólag késő este a ponthatár..."
|
| Előzmény: [897] Csimby, 2005-04-29 19:15:31 |
|
| [903] Lóczi Lajos | 2005-05-04 22:09:28 |
 Következzék egy régi feladat:
162. feladat. Tekintsünk két kört, K1-et és K2-t, sugaraik legyenek rendre 1, illetve r egység. K2 középpontja K1 peremén helyezkedik el. Mekkorának válasszuk r értékét, hogy a két körlap metszetének területe K1 területének fele legyen?
|
|
| [902] Atosz | 2005-05-04 17:53:49 |
 Sziasztok!
Kissé eltűntem az utóbbi időben, de újra itt vagyok, s gondolom ilyenkor illik egy új feladattal visszatérni. Nem túl nehéz.
[161]. feladat
A távoli hegyi faluban akkor tartanak ünnepet, amikor a kolostor és a templom harangjai pontosan egyszerre konganak. Mindkét harangot szabályos időközönként, egész számú percenként kongatják; de természetesen más ritmusban. Ma a harangok déli 12-kor fognak együtt kongani. Az ünnepnapok között a harangok felváltva konganak, és előfordul, hogy a nem ünnepnapok egyikén csak egy percnyi eltérés választja el a két hangot. Legutóbb a harangszók egybeesése déli 12 órakor történt, az azóta eltelt napok száma prímszám.
Hány napja történt ez?
Jó fejtörést hozzá!
|
|
|
| [900] BohnerGéza | 2005-05-03 12:49:15 |
 Kedves Csimby!
Sajnos az asztroidra vonatkozó feltevésed nem jó. Kiszámoltam, egységnyi sugarú körben az asztroid hossza 6, a kör kerülete 2*PI.
(A számolás egy egyszerű integráláshoz vezet.)
|
| Előzmény: [884] Csimby, 2005-04-26 22:06:56 |
|
|
| [898] levi | 2005-04-29 21:47:06 |
 Nagyon érdekelne hogy hogyan lehet eljutni ahhoz a kitevőhöz (szóval tulajdonképpen a megoldás érdekelne)... persze csak ha el lehet árulni...
|
|
| [897] Csimby | 2005-04-29 19:15:31 |
 Más kérdés:
Tudja valaki, hogyan határozzák meg a felvételi ponthatárokat, milyen algoritmussal? (Ez ugyanis csöppet sem tűnik egyértelműnek)
|
|
| [896] Lóczi Lajos | 2005-04-29 17:05:01 |
 Igen, csak véletlen.
A keresett kitevő ugyanis megközelítőleg  =0.561493300750... (melyhez tartozó =0.561493300750... (melyhez tartozó 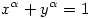 -alakzat kerülete az egységkör kerületétől csak kb. 10-12-nel tér el.) -alakzat kerülete az egységkör kerületétől csak kb. 10-12-nel tér el.)
|
| Előzmény: [895] Csimby, 2005-04-29 16:42:04 |
|
|
|
|
|
|
|
|
|
|
|
| [884] Csimby | 2005-04-26 22:06:56 |
 A kis kör sugara a nagy kör sugarának a negyede, az animációból látszik, hogy az asztroid és a nagy kör kerülete megegyezik. (egy negyed körív = egy negyed asztroid ív = a kis kör teljes kerülete)
|
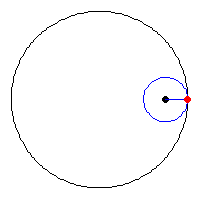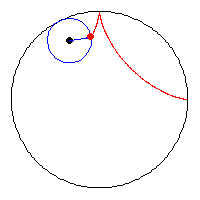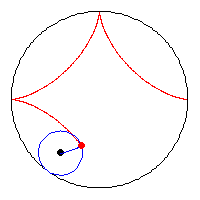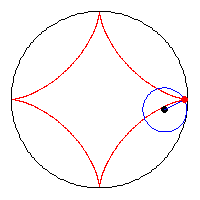 |
| Előzmény: [883] Csimby, 2005-04-26 22:02:49 |
|
|
| [882] nadorp | 2005-04-25 12:29:33 |
 Szia Csimby !
A 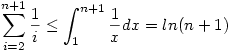 egyenlőtlenség módszerére gondoltam. Ugyanis: egyenlőtlenség módszerére gondoltam. Ugyanis:
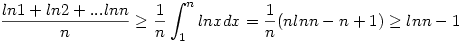 ,azaz ,azaz 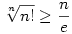 . .
A fent kapott egyenlőtlenség már jó alap a feladatban a nemkorlátosság bizonyításához.
|
| Előzmény: [881] Csimby, 2005-04-22 21:54:35 |
|
|
|
|
| [878] nadorp | 2005-04-21 11:14:46 |
 Jelentkező hiányában lelövöm a 160. feladatot.
Legyen x az a nyerőszám, amely bármely kettő nyerőszám összegének az osztója. Ekkor, ha y egy másik nyerőszám, akkor x | x+y miatt x| y is teljesül. Tehát x olyan nyerőszám, amely az összes nyerőszám osztója. Ebből következik, hogy 5x 90, azaz x 90, azaz x 18. Másrészt, mivel x ismeretében az összes többi nyerőszám egyértelműen meghatározható, ezért 6x>90 is teljesül, azaz x>15. Így x=16,17,18 jöhet csak szóba. Mivel a paritás x-et meghatározza, ezért x=17. A nyerőszámok 17,34,51,68,85. 18. Másrészt, mivel x ismeretében az összes többi nyerőszám egyértelműen meghatározható, ezért 6x>90 is teljesül, azaz x>15. Így x=16,17,18 jöhet csak szóba. Mivel a paritás x-et meghatározza, ezért x=17. A nyerőszámok 17,34,51,68,85.
|
| Előzmény: [877] lorantfy, 2005-04-18 22:42:47 |
|
| [877] lorantfy | 2005-04-18 22:42:47 |
 160. feladat: Mivel nagy nyeremény várható a lottón Mézga Aladár úgy döntött megkérdezi Köbükit, mik lesznek a nyerőszámok.
- A számokat nem mondom meg, de azt elárulhatom, hogy van köztük olyan szám amellyel bármely két nyerőszám összege osztható.
- Mi ez a szám?
- Ha megmondanám, akkor kitalálnád a nyerőszámokat.
- Legalább azt áruld el, páros vagy páratlan ez a szám.
A válasz után Aladár kitalálta a számokat, megjátszotta őket és nyert.
Mik voltak a nyerőszámok?
|
|
| [876] Csimby | 2005-04-17 21:02:14 |
 Ezt most találtam, Ramanujan egyik formulája. Csak érdekességnek rakom fel, szép nem?
|
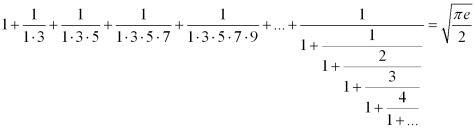 |
|
| [875] Hajba Károly | 2005-04-08 15:28:33 |
 Kedves (mindent) tudniakarok!
Egy újszülöttnek minden vicc új, de nem a véneknek. :o) Szóval anno, valamikor a '90-es években valamelyik magyar ált. isk. diákjai lelkes matektanáruk irányításával egy nagyszabású kisérletet tettek a betetted feladat megvalósítására. Két napon keresztül többezer gyufaszálat v. akármit ejtegettek le több csoportba szerveződve. Ha jól emlékszem 2 tizedesjegy pontossággal ki is hozták a  értékét. Ez akkor világcsúcs volt. értékét. Ez akkor világcsúcs volt.
Érdekes lehet az betett ábra egyéb formái is.
HK
|
| Előzmény: [874] tudniakarok, 2005-04-08 14:11:29 |
|
| [874] tudniakarok | 2005-04-08 14:11:29 |
 Na ez érdekes,nagyon...
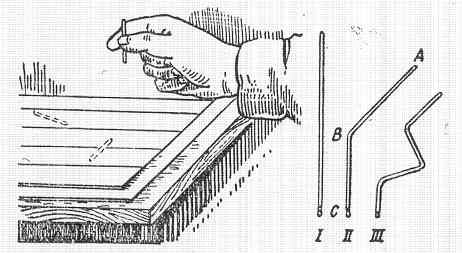
159.feladat: Tulajdonképpen a feladat nem más, mint egy kísérlet, amit egy Buffon nevű matematikus agyszüleményeként tartanak számon:
Felszereljük magunkat egy rövid, kb. 2 cm hosszú varrótűvel. /A varrótű végei legyenek letörve, és persze az a jó, ha hossza mentén egyenletes vastagságú/. Ez után egy papírlapon vékony párhuzamos vonalakat húzunk, amelyeknek egymástól való távolsága kétszer olyan nagy, mint a tű hossza. Ezután bizonyos (tetszés szerinti, de állandó) magasságból a tűt a papírra ejtjük és megfigyeljük, hogy metszi-e a tű a vonalak valamelyikét, vagy nem. Hogy a tű ne ugrálhasson, a papírlap alá itatóst vagy posztót teszünk.A tűdobálást sokszor megismételjük, (legalább százszor, ezerszer, vagy esetleg 28 milliószor) és minden alkalommal megnézzük, hogy volt-e metszés. (megj.: Metszésnek számít az az eset is, amikor a tű csak a hegyével érinti a vonalat.) Ha ezután a dobások számát elosztjuk a metszések számával milyen eredményt kapunk?
|
 |
|
|
| [872] jonas | 2005-03-30 18:22:06 |
 Szerintem a 3×3-as felosztásból az is látszik, hogy legfeljebb 9 lyuk maradhat, tehát 11 dominó mellé mindig le lehet rakni még egyet. Egy 3×3-as sarokban ugyanis hat mezőt mindig le kell fedni ahhoz, hogy ne lehessen még egy dominót lerakni. Ez az eredmény megegyezik Gézáéval, és éles is, mert 12 dominó már meg tudja tölteni a táblát.
|
A |
A |
|
B |
|
| C |
C |
|
D |
B |
E |
|
F |
F |
D |
|
E |
| G |
|
H |
I |
I |
|
| G |
J |
H |
|
K |
K |
|
J |
|
L |
L |
|
|
|
| Előzmény: [852] Csimby, 2005-03-29 01:19:33 |
|
| [871] tudniakarok | 2005-03-29 21:56:19 |
 azaz ezért jó a tiéd nem pedig nem jó!na mind1
|
|
| [870] tudniakarok | 2005-03-29 21:49:17 |
 Bár ez meg pl 8-ra nem jó,mert ott 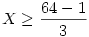 ebből X=21, amit irtál ott meg 22 jön ki (66/3) ebből X=21, amit irtál ott meg 22 jön ki (66/3)
|
|
| [869] tudniakarok | 2005-03-29 21:39:43 |
 Igazad lehet,sőt van!Belebonyolódtam az oszthatóságba!Ez is meg van!
|
|
|
| [867] Csimby | 2005-03-29 21:17:59 |
 k=4-re azt mondja, hogy legalább 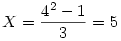 dominót el tudunk helyezni. De szerintem ez az érték 6 kéne, hogy legyen. Vagyis N=6 míg a képlettel N=42-2*5+2=8. Nekem gyanús, hogy k=5-re sem jó, vagyis akkor van baj, amikor k2-1 osztható 3-mal (k=2-re sem jó, míg k=3-ra, és k=6-ra, amikor k2-1 nem osztható 3-mal, olyankor jó). dominót el tudunk helyezni. De szerintem ez az érték 6 kéne, hogy legyen. Vagyis N=6 míg a képlettel N=42-2*5+2=8. Nekem gyanús, hogy k=5-re sem jó, vagyis akkor van baj, amikor k2-1 osztható 3-mal (k=2-re sem jó, míg k=3-ra, és k=6-ra, amikor k2-1 nem osztható 3-mal, olyankor jó).
|
| Előzmény: [866] tudniakarok, 2005-03-29 20:07:52 |
|
| [866] tudniakarok | 2005-03-29 20:07:52 |
 Na akkor kxk-s táblára lerakható még egy dominó,ha N db mező szabad,és X-1 db dominó van lerakva: Kós Géza nyomán: 6X 2(k-1)2+4k-4 ,ebből 2(k-1)2+4k-4 ,ebből
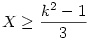
Minden term. szám négyzete vagy osztható 3-mal vagy 1 maradékot ad,ezért
![X=\bigg[\frac{k^2+1}{3}\bigg]](keplet.cgi?k=44CD375480E1B13C) ez a legkevesebb dominó ,ami lerakható a táblára,azaz ez a legkevesebb dominó ,ami lerakható a táblára,azaz
![k^2-2\bigg[\frac{k^2+1}{3}\bigg]](keplet.cgi?k=9308E9F3258B329F) helyünk marad miután az összeset leraktuk,ezért helyünk marad miután az összeset leraktuk,ezért
![N=k^2-2\bigg[\frac{k^2+1}{3}\bigg]+2](keplet.cgi?k=CF3759D7090A57FE)
Nekem eddig minden próbálkozásnál összejött,de azért nem állítom hogy teljesen jó.
|
| Előzmény: [864] levi, 2005-03-29 17:02:04 |
|
| [865] Kós Géza | 2005-03-29 17:29:59 |
 Helyezzünk el k darab dominót úgy, hogy több már ne férjen a táblára. Azt kell megmutatni, hogy k 12. 12.
Számoljuk össze az olyan dominó-rácspont párokat, amikor a rácspont a dominó határán van.
a) Minden dominó határán 6 rácspont van, ez tehát összesen 6k pár.
b) A tábla belsejében levő 25 rácspont mindegyikének legalább két dominóhoz kell illeszkednie, különben még egy dominót odatehetünk mellé. A tábla kerületén levő rácspontokhoz is --- a sarkokat kivéve --- illeszkednie kell legalább egy-egy dominónak. Ilyen rácspontból 20 van. A párok száma tehát legalább 25.2+20.1=70.
Azt kaptuk, hogy 6k 70, vagyis k 70, vagyis k 12. 12.
|
| Előzmény: [863] tudniakarok, 2005-03-29 15:49:34 |
|
| [864] levi | 2005-03-29 17:02:04 |
 Az N számnak mindig párosnak kell lennie, nem? A k szám páros, k*k is páros, és ha elhelyezek egy dominót, akkor mindig 2-vel fog csökkeni, azaz páros lesz mindig a nem üres mezők száma is és a fedett mezők száma is. A sejtés azonban k=8 esetre ez alapján nem jó, mert akkor X=27, ami nem lehetséges.
|
| Előzmény: [859] tudniakarok, 2005-03-29 15:23:03 |
|
| [863] tudniakarok | 2005-03-29 15:49:34 |
 Íme az én bizonyításom a saját feladatomra!: Úgy indulok,ahogy Csimby:Osszuk fel a 6x6-os táblát 4db 3x3-as négyzetre! Mivel 14 mező fedetlen,ezért van olyan résztábla amelyen 4 fedetlen mező van.Megmutatjuk hogy ezen résztáblán van 2 szomszédos mező!Legyen a résztábla a táblázat jobb felső sarka! Tegyük fel hogy az állítással ellentétben nincs 2 szomszédos mező! Ekkor az A B C betűkkel jelölt mezők nem lehetnek fedetlenek,hisz akkor a közbezárt mező is fedetlen volna. Hasonlóan nem lehetnek fedetlenek az x-szel jelölt mezők sem,hiszen akkor C sarokmező is fedetlen volna. Vagyis a bal oldali 2x3-mas táblarészen legalább 4 mező le van fedve,így legfeljebb 2 mező lehet fedetlen! Emiatt az alsó sorban kell lenni 2 fedetlen mezőnek. Feltevésünk szerint nics 2 szomszédos mező,tehát ez a 2 csak a két szélső lehet. Tehát E és F biztosan nincs lefedve. Ebből viszont adódik,hogy a szürke mezőknek fedettnek kell lenni,különben volna 2 szomszédos fedetlen mező. Ugyanakkor az A és C mezők közötti mezőnek is fedettnek kell lenni. Ezt viszont nem lehet megtenni,mert ez a dominó az A B C mezők egyikét lefedné,így nem maradhatna 4 fedetlen mező! Ellentmondásra jutottunk,tehát van két szomszédos fedetlen mező!
|
 |
|
| [862] levi | 2005-03-29 15:45:07 |
 Bocs, már megint nem fogalmaztam pontosan, szóval N az üres mezők száma, de szerencsére valaki rá tudott jönni...
|
|
| [861] tudniakarok | 2005-03-29 15:26:31 |
 ÁÁÁÁÁÁÁ! Ne!!! Igazad van Csimby 14 mező fedetlen vissza az egész,de még ma beírom az én bizonyításom is
|
|
| [860] tudniakarok | 2005-03-29 15:24:25 |
 De ha gondolod beírhatom az én bizonyításom is mert csak a vezérfonal ugyanaz,mint a tiéd,de hát az a lényeg
|
|
| [859] tudniakarok | 2005-03-29 15:23:03 |
 Úgy látom mindenkit félreértek!Bocs! Levit úgy értettem meg,hogy végigböngészetem 16szor amit írt meg az enyémet is itthon,és nekem is kijött úgy ahogy Levinek,úgyhogy egyetértek vele! Na de akkor legyen X az a darabszám amit egy kxk-s táblán lerakva még egyet le tudunk rakni (6x6-osnál X=14) Tehát amit sejtek: 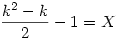 és szerintem legyen k>2 és szerintem legyen k>2
|
|
| [858] Csimby | 2005-03-29 15:16:46 |
 "ugye bizonyítottuk hogy 6x6os táblán 14et elhelyezve még egyet le tudunk rakni,tehát 15öt"
Nem!
Azt bizonyítottuk, hogy ha 11 dominót már leraktunk, akkor biztosan el tudunk helyezni még egyet, vagyis 12-t összesen...
|
| Előzmény: [856] tudniakarok, 2005-03-29 15:04:29 |
|
| [857] Csimby | 2005-03-29 15:13:58 |
 Úgy konkrétan miből értetted meg Levit, ebből: "ha ott is megvizsgálnánk a további sorokat, kijönne az, hogy nem lehet üres mezőt elhelyezni... "? ;-) Egyébként meg szerintem az én bizonyításom (és ezek szerint ilyen a tiéd is) egyáltalán nem hosszú, dehát ízlések és pofonok...
Tényleg nem teljesen világos, de Levinél N nem az elhelyezett dominók száma, hanem az üresen maradt mezők száma úgy, hogy biztosan el tudjunk helyezni még egy dominót (láthatod ezt abból is, hogy k=6-nál N=14, ami a te feladatod). Így stimmel a k=2 és k=4 esetre adott N=2 és N=6.
|
| Előzmény: [855] tudniakarok, 2005-03-29 14:47:26 |
|
| [856] tudniakarok | 2005-03-29 15:04:29 |
 Hopp egy ötlet: azt kell megnézni hogy mennyi helyünk marad a táblán, ha lerakjuk azt az utolsó dominót is, ugye bizonyítottuk hogy 6x6os táblán 14et elhelyezve még egyet le tudunk rakni,tehát 15öt,ez 15x2=30 négyzetet foglal a 36-ból,azaz 6 négyzet üresen marad. 2x2es táblát kizárom,nem érdemes vele foglalkozni! 3x3as táblán N=2-nél még egyet le tudok rakni,azaz 6 négyzetet fedek,3 maradt üresen! 4x4es táblán N=5-nél még egyet lerakva 12 négyzetet fedek,4 maradt üresen!Még nem láttam be,de a sejtés hogy kxk-s táblán k marad üresen,és így: 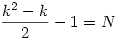
|
|
| [855] tudniakarok | 2005-03-29 14:47:26 |
 Most már értem levit!:) Az én megoldásom szinte ua mint a Csimbié,úgyhogy nem írom be,mert hosszú! Viszont levi azt írja hogy 2x2-es táblán 2-őt elhelyezek és még biztosan el tudok helyezni egyet,lehet hogy én nem értem megint,de ha 2őt elhelyezek,akkor már nincs több hely,mert lefedi az egészet! Ha k=4 akkor szerintem N=5,nem pedig 6.talán
|
| Előzmény: [854] levi, 2005-03-29 13:49:07 |
|
| [854] levi | 2005-03-29 13:49:07 |
 Jonasnak igaza van, a többi sorban nem feltétlenül működik, azonban ha ott is megvizsgálnánk a további sorokat, kijönne az, hogy nem lehet üres mezőt elhelyezni... a közérthetetlenségemért meg elnézést kérek, egyszerűen csak nem tudok fogalmazni... Viszont felmerült bennem egy kérdés: Adott egy k pozitív páros szám. Egy k*k-ás táblázatban elhelyezünk néhány dominót. Melyik az a legkisebb N szám, amelyre igaz, hogy még mindenféleképpen el lehet helyezni még egy dominót, anélkül, hogy a már letett dominókat elmozdítanánk?
k=2-nél szerintem ez 2, k=4-nél talán 6, k=6-nál akkor 14.
|
| Előzmény: [851] tudniakarok, 2005-03-28 23:22:47 |
|
| [853] Csimby | 2005-03-29 01:23:19 |
 A számozásra végül nem lett szükség csak az elején ezt még nem tudtam...
|
|
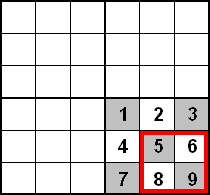
| [852] Csimby | 2005-03-29 01:19:33 |
 Szerintem bontsuk fel 4 db. 3×3-as négyzetté a 6×6-os négyzetet. Ugye 14 üres mező marad összesen, vagyis lesz olyan 3×3-as négyzet amelyben legfeljebb 5 mezőt fed le dominó (ha mindegyikben legalább 6 mezőt fedne le dominó, akkor 4×6=24, 24+14=38 > 36, ami ellentmondás).
A szimetria miatt mindegy, hogy melyik 3×3-as négyzetben bizonyítjuk, hogy ha csak 5 mezőt fedünk le belőle dominókkal, akkor még egy dominót el tudunk helyezni, tehát legyen ez a jobb alsó 3×3-as négyzet.
Ahhoz, hogy a piros négyzetben ne maradjon hely domionónak, ahhoz mindenképpen el kell helyeznünk 2 teljes dominót a 3×3-as négyzetben. Vagyis biztosan lefedünk 2 szürke és 2 fehér mezőt. Az 5. mező lefedése után tehát vagy 3 szürke és 1 fehér, vagy pedig 2 fehér és 2 szürke mezőnk marad.
Mindegyik fehér mezőnek 3 szürke szomszédja van, tehát bármely fehér mezőhöz csak 2 olyan szürke mező létezik, amely nem mellette található, így ha 3 szürke és 1 fehér mező marad üresen, akkor biztosan lesz hely még egy dominónak.
2 fehér mezőnek vagy 4 vagy 5 szürke szomszédja van, tehát akárhogy is marad üresen 2 szürke és 2 fehér mező, biztosan lesz 2 egymás melletti és így biztosan lesz hely még egy dominónak.
|
 |
| Előzmény: [848] tudniakarok, 2005-03-27 11:42:56 |
|
| [851] tudniakarok | 2005-03-28 23:22:47 |
 Őszintén szólva,én is az "elegánsabb" megoldás reményében írtam be a feladatom,mert az én bizonyításom is legalább ilyen hosszú.Ettől függetlenül én is csak az elejét értem a bizonyításodnak...(mondjuk Einsteint sem értették:) Talán vmi ábrával szemléltetve felfognánk mit mondasz!?
|
| Előzmény: [849] levi, 2005-03-28 15:15:47 |
|
| [850] jonas | 2005-03-28 21:57:55 |
 Ezt a bizonyítást nem egészen értem. Az világos, hogy ha a legfelső sorban három lyuk van, akkor nem lehet a következőben egynél több. Viszont úgy tűnik, hogy a bizonyîtásban ezt nem csak az első sorra, hanem a többire is kihasználod, ezekre pedig már nem tudon, miért lenne igaz.
|
| Előzmény: [849] levi, 2005-03-28 15:15:47 |
|
| [849] levi | 2005-03-28 15:15:47 |
 Elképzelés a 158. feladatra: Tehát próbáljunk meg 14 üres mezőt úgy elhelyezni ezen a táblázaton, hogy a maradék 22-n mind legyen dominó. Mivel 6 sorunk és oszlopunk van, belátható, hogy 2 sorban és oszlopban legalább 3 üres mező lesz. Azt kell belátnunk, hogy nem tudunk úgy elhelyezni 14 üres mezőt, hogy a nem üreseket pedig dominó fedje. Vizsgáljuk csak a sorokat! Ha az első sorban 3 üres mezőt kívánunk elhelyezni, azt kétféleképpen tehetjük meg: (D a dominóval fedett, Ü az üres mező): (1) ÜDÜDÜD (vagy ennek szimmetrikus változata) ill. (2)ÜDÜDDÜ (és ennek is a szimmetrikus változata). A szimmetrikus változatok vizsgálatát elhagyhatjuk, hiszen azok lényegében ugyanazok mint az eredetik. Először nézzük meg, hogy ha egy sorban 3 üres mező van, akkor a következő sorban mennyi üres mező lehet maximum. Az (1) esetén 0, míg a (2) esetén 0 vagy 1. Nézzük az (1) elrendezést! Ekkor a második sorban DDDDDD lesz, hiszen az első sor 1.,3.,5. kockája alatt nem lehet üres mező, mert akkor lenne üres pár, így a második sor 1.,3.,5. mezője D-s lesz, a 2.,4.,6. mező pedig az első sor dominói miatt lesznek fedettek. Tehát a maradék 4 sorban 11 üres mezőt kellene elhelyeznünk. Mivel egy sorban 0,1,2,3 üres mező lehet és a 11-et 4 tag összegeként a 0,1,2,3 segítségével csak 2+3+3+3-ként lehet felírni, ezért a maradék 4 sorból háromban is 3 üres mezőnek kell szerepelnie. De ha a 3. sorban 3 üres mező van, akkor a következőben legfeljebb egy lehet, azaz a hátramaradó kettőben 7nek kell lennie, ami lehetetlen. Ha a harmadik sorban 2 üres mező van, akkor a negyedik már biztos 3 van, de az után legfeljebb csak egy lehet az ötödikben, azaz a hatodikban 5nek kell lennie, ami szintén lehetetlen. A (2) esetben a 2. sorban a legjobb esetben 1 üres mező szerepel. Az a maradék négy sorban 10. Ez kétféleképpen írható fel a 0,1,2,3 számok 4tagú összegeként: 1+3+3+3 vagy 2+2+3+3. Erről a két lehetőségről is könnyen beláthatjuk, hogy nem lehetségesek (hasonlóan mint az (1) esetben). Ha az első sorban 2 üres mező szerepel, azzal nem változott semmi, hiszen a 2 db 3 üres mezős sor elhelyezése abban az esetben sem lehetséges. Tehát beláttuk, hogy nem lehet elhelyezni 14 üres mezőt, úgy hogy a maradék 22-n mind dominó legyen, azaz legalább egy üres mező-pár lesz, azaz elhelyezhetünk még egy dominót úgy, hogy ne kelljen elmozdítani amár lerakott dominókat. (Picit hosszú megoldás, jobb lett volna egy rövidebb, "elegánsabb", de olyat nem találtam... talán valaki más...)
|
| Előzmény: [848] tudniakarok, 2005-03-27 11:42:56 |
|
| [848] tudniakarok | 2005-03-27 11:42:56 |
 Egy unalmas irodalomóra szüleménye!(szerintem érdekes lett)
158. feladat: Egy 6x6-os táblázatra néhány dominót helyezünk, hogy mindegyik pontosan 2 mezőt fed le. Bizonyítsuk be,hogy ha 14 mező fedetlen,akkor még egy dominót a táblára helyezhetünk,úgy hogy a többit a helyén hagyjuk!
|
|
|
| [846] Kemény Legény | 2005-03-17 16:47:25 |
 Na egy érdekes feladat:Lehet-e 6 egymást követő pozitív egész szám szorzata egy egész szám 5. hatványa?
|
|
| [845] Lady | 2005-03-15 11:39:38 |
 (4x+3)(x-5).3=(2x+21)(x-2).6 Vezesd le a következő lépést.Kösz
|
|
|
|
|
| [841] jonas | 2005-03-11 16:57:16 |
 Ez érdekes. Hárommal persze meg tudom csinálni (veszek három egymásra merőleges téglalapot úgy, hogy a csúcsaik egy szabályos ikozaéder csúcsait alkossák, és ezeknek a kerülete megfelel), de nem tudtam, hogy háromnál többel is lehet.
|
| Előzmény: [839] Atosz, 2005-03-10 16:34:37 |
|
| [840] Hajba Károly | 2005-03-10 16:48:01 |
 Üdv Atosz!
Ne is! Aki nem ismeri, hadd gondolkozzon rajta. A megoldhatóság is egyfajta segítség már. Én is azután tudtam megoldani, miután közölték, hogy létezik megoldás. :o)
HK
|
| Előzmény: [839] Atosz, 2005-03-10 16:34:37 |
|
| [839] Atosz | 2005-03-10 16:34:37 |
 Kedves Onogur!
Nem csak hármat, akármennyit lehet úgy, hogy szétnyitás nélkül megbonthatatlanul egyben marad, de bármelyiket nyitjuk, darabjaira hullik az egész. Még nem rajzolom be a megoldást, mert ismerem a feladatot!
|
| Előzmény: [838] Hajba Károly, 2005-03-10 11:54:41 |
|
| [838] Hajba Károly | 2005-03-10 11:54:41 |
 Kedves Betti!
Köszi a kiegészítést.
157. feladat:
Lehet-e 3 karikát nem szétesően úgy egymásba fűzni, hogy bármelyik kinyítása esetén a másik kettő is szabaddá válik.
HK
|
|
|
|
| [835] Hajba Károly | 2005-03-09 09:30:49 |
 Csak nem egy viharfelhő, akarom mondani 2 szintű elektronfelhő síkmetszete. Nem. Egy metapárt szimboluma (CS-NY-P). De ez sem. Inkább egy részeg nyolcas. Szóval a megoldás végtelen. :o)
HK
|
| Előzmény: [834] Lóczi Lajos, 2005-03-08 22:11:47 |
|
| [834] Lóczi Lajos | 2005-03-08 22:11:47 |
 156. feladat: Mi lesz az x2-y2=1 egyenletű hiperbola képe annál az inverziónál, melynek alapköre az origó középpontú egységkör?
|
|
| [833] Atosz | 2005-03-07 18:30:42 |
 Kedves Onogur!
Én inkább egy olyan bonyolításon törtem a fejem, hogy ugyanígy 2 gyerek és 1 kutya van, csak a sebességeket kellene belőni úgy, hogy minél hamarabb jussanak át mindhárman, annyi megkötéssel, hogy a gyalog-sebességek összege legyen 8 km/h, a bicaj-sebességek összege pedig legyen 40 km/h. Azaz az eredeti feladat szerinti sebességösszegeket kellene szétosztani hármójuk között úgy, hogy minél hamarabb átjussanak.
Természetesen előbb kiszámoljuk a tiedet, majd utána jöhet ez.
Lászlónak! Örülök, hogy tetszenek a példák - bár én tudnék ilyeneket kitalálni - a lényeg az, hogy én pont azokat kedvelem, melyeket egyszerűen meg lehet fogalmazni, mégis az első gondolatunk esetleg tévútra vezet. (lehetetlennek tűnik)
|
| Előzmény: [832] Hajba Károly, 2005-03-07 15:47:53 |
|
| [832] Hajba Károly | 2005-03-07 15:47:53 |
 155. feladat:
Bonyolítsuk tovább Atosz 153. feladatát; most találtam ki, lehet, hogy tele lesz törttel:
A, B, C és D személy közösen 20 km útra indulnak 1 biciklivel. 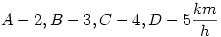 sebességgel képes haladni, míg a bringával mindenki sebességgel képes haladni, míg a bringával mindenki 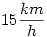 sebességgel képes haladni. Mennyi idő alatt tudnak leghamarabb célba érni? sebességgel képes haladni. Mennyi idő alatt tudnak leghamarabb célba érni?
HK
|
|
|
| [830] lorantfy | 2005-03-07 14:02:13 |
 Kedves Atosz!
Jók a példák! Főleg a bicajos. Ha lesz egy kis időm átdolgozom egy kicsit, hogy lehessen csomagtartón is szállítani...
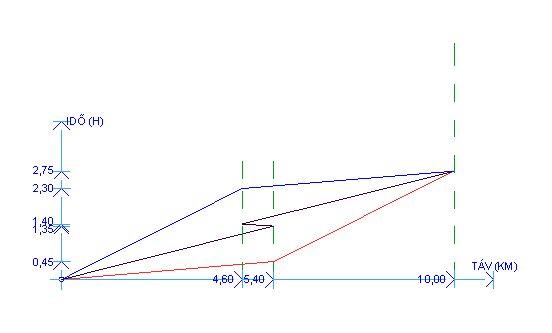
153. feladathoz: A szöveg ábrává formálva itt látható. Ebből már könnyű felírni az egyenleteket. A D-vel és E-vel jelölt eltelt idők mindkét személynél egyenlőek. A megoldás x=11.
![[x+\frac{9y}{4}-(86-x)]\frac{15}{16}=86-x](keplet.cgi?k=B9C141C7734E6914)
2y-x=y-(86-x)
|
 |
| Előzmény: [829] Atosz, 2005-03-07 09:14:54 |
|
| [829] Atosz | 2005-03-07 09:14:54 |
 Sziasztok!
László, nagyon ötletes - és jó! - a levezetésed a bicajos feladatra. Remélem megtetszett! Természetesen megvalósítható (matematikai értelemben persze - lopás kizárva): Az egyik gyerek 5.4 km-t teker előre, majd a kutya 0.8 km-t vissza. Így mindhárman egyszerre érkeznek be.
Természetesen a másik feladatra adott megoldásod is jó, így csak gratulálni tudok!
|
| Előzmény: [828] lorantfy, 2005-03-07 01:25:20 |
|
| [828] lorantfy | 2005-03-07 01:25:20 |
 Kedves Atosz!
Hát persze, hogy a 153. feladatot is megcsináljuk. Már korábban a suliban egyik szünetben próbálkoztam vele, de nem lett egész és egy életkoros feladatban nem egész szám csak az emeltszintű érettségin lehet, így elment a kedvem tőle.
Aztán most felszólításodra átolvastam mégegyszer és kijött, hogy én 75 éves vagyok, kis barátom meg 11 éves. Aki nem hiszi, járjon utánna!
|
| Előzmény: [826] Atosz, 2005-03-06 18:38:23 |
|
| [827] lorantfy | 2005-03-06 23:49:20 |
 Hello Csimbi!
Kösz az ötletet. Hogy én erre nem jöttem rá :-) Ebből is látszik, hogy a vasárnapi ebéd után kevés vér jut az ember agyába.
Hát akkor kerékpározzon visszafelé a kutyus attól a ponttól, ahol Juliska hagyta a bicajt, mondjuk t ideig. Így 16t utat tesz meg, ezt visszafelé 4 km/h sebességgel 4t alatt fogja megtenni, vagyis 5t idővel nő a menetideje.
És mennyit nyer rajta a két gyerek. A 16t utat kettőjük között egyenlően kell elosztani. Tehát Juliska 8t-vel tovább megy mint az út fele. A kutya visszahozza 16t-vel és így Jancsi is 8t-vel többet biciklizhet. Most a 8t utat 2 km/h helyett 12 km/h sebességgel tudja megtenni, így a nyereség 8t/2 - 8t/12 = (10/3)t
Az előző gondolatmenet szerinti menetidők különbsége 25 perc volt. Növelje a kutyus annyivel a menetidejét, hogy éppen egyenlő legyen Jancsi és Juliska új csökkentett menetidejével, így pont együtt fognak beérni.
(10/3)t+5t = 25perc, amiből t=3perc, akkor 5t=15-perccel nő a kutya menetideje és ennyi lesz J és J ideje is.
Tehát az elérhető csúcsidő: 2 óra 45.
Az első gyerek akkor 5+8t=5+24/60 = 5,4 km-ig kerekezik és ott leteszi a bicajt.
Hát, gondoljátok végig, hogy ez megvalósítható-e! (Mi van ha közben ellopják a kerékpárt?)
Az lenne még kutyajó, ha a kerékpáron lenne csomagtartó és egyik szállíthatná a másikat!
|
| Előzmény: [825] Csimby, 2005-03-06 15:23:15 |
|
| [826] Atosz | 2005-03-06 18:38:23 |
 Sziasztok!
Már azt hittem, hogy senkit sem fog meg ez a különleges feladvány. A "csavar" Csimby gondolatában van, azt egy picit még tovább lehet fejleszteni. A szélsőérték-probléma nyilván az, hogy meddig menjen előre az első gyerek, meddig vigye vissza a kutya a bicajt, hogy végül mindhárman egyszerre érjenek be. Ennek kidolgozását azért rátok bízom.
A feladatnak egyébként komoly matek-irodalma van, hiszen azt hinnénk elsőre, hogy László megoldása nem javítható - és mégis (lásd Csimby) Ehhez persze meglepő módon viszafelé kellett bicajozni egy szakaszon.
1. Masuda, S. (1970). "The bicycle problem," University of California, Berkeley: Operations Research Center Technical Report ORC 70-35.
2. Chvatal, V. (1983). "On the bicycle problem," Discrete Applied Mathematics 5: pp. 165 - 173.
Remélem az előtte lévő feladatot is megoldjátok! Jó munkát!
|
|
| [825] Csimby | 2005-03-06 15:23:15 |
 Ha a kutya, mikor eléri az otthagyott biciklit, visszaviszi azt annak a gyereknek, aki addig sétált, akkor a gyerekek többet tudnak biciklizni az út felénél. Így nekem kijött egy megoldás, amivel kevesebb mint 2 óra 50 perc alatt megjárják az utat.
|
| Előzmény: [824] lorantfy, 2005-03-06 13:31:57 |
|
| [824] lorantfy | 2005-03-06 13:31:57 |
 Hello Atosz!
154. feladathoz: Ha a kutya nem biciklizik, csak végigsétál, akkor 2 óra 30 perc alatt teszi meg az utat. Jancsi és Juliska felesben használva a bicajt - hogy egyszerre érjenek be - 2 óra 30 perc séta + (5/12)*60=25 perc biciklizés után= 2 óra 55 perc alatt érnek be a célba.
Ha a kutya bicajozna, az csak növelné az időt, hiszen Jancsi és Juliska ezalatt lassabban haladna.
Nekem így túl egyszerűnek tűnik. Lehet hogy valamit félreértettem?
A kerékpár felesben való használatát úgy értettem, hogy pl. Juliska elmegy az út feléig. Ott letámasztja a bicajt egy fához és továbbindul gyalog. Mikor Jancsi odaér a bicajhoz, felpattan rá és azzal megy tovább.
Ha nem hagyhatják el a bicajt, hanem kézből-kézbe kell adni, akkor meg nem tudják vele csökkenteni a menetidőt és csak 5 óra alatt tudnak beérni.
Remélem van benne még valami csavar! Vagy csak az adatokat adtad meg rosszul?
|
| Előzmény: [821] Atosz, 2005-03-04 10:16:30 |
|
| [823] Atosz | 2005-03-04 19:48:42 |
 Szia Csimby!
Most, hogy visszanéztem, tényleg azt beszéltétek egymás közt nadorppal, hogy várakozunk, de nem vettem észre! (legalábbis nem volt eszemben) Mégegyszer bocsi!
|
| Előzmény: [822] Csimby, 2005-03-04 13:14:43 |
|
|
| [821] Atosz | 2005-03-04 10:16:30 |
 Nemrég feltettem [153.] számmal egy "egyszerű" egyismeretlenes egyenlettel is megoldható feladatot. Egyelőre még senki sem írt be megoldást, de addig is itt egy újabb érdekesség:
[154.] feladat Egy fiú, egy lány és egy kutya 10 km-es útra indulnak. A fiú és a lány 2 km/h-val haladnak, a kutya 4 km/h-val. Van azonban egy biciklijük, amit mind a hárman (a kutya is) használhatnak, de egyszerre csak az egyikük. A fiú és a lány 12 km/h-val tud biciklizni, a kutya 16 km/h-val. Mi az a legrövidebb idő, ami alatt mindhárman célba érnek?
|
|
| [820] Atosz | 2005-03-04 09:59:10 |
 Ha jól láttam Csimbynek ez a feladata (127) még megoldatlan. Nekem gyorsan kijött a harmonikus sor és a mértani közép közti egyenlőtlenség, illetve a harmonikus sor és a természetes logaritmus közti kapcsolat alapján. Tényleg nem volt nehéz.
|
| Előzmény: [804] Csimby, 2005-02-27 16:20:12 |
|



 belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor
belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor 

 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2
4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2












 )
) R deriválható függvényt tetszőlegesen úgy, hogy 0
R deriválható függvényt tetszőlegesen úgy, hogy 0 (0,1)
(0,1)  1
1 
 . A kerület 8r + 2r
. A kerület 8r + 2r


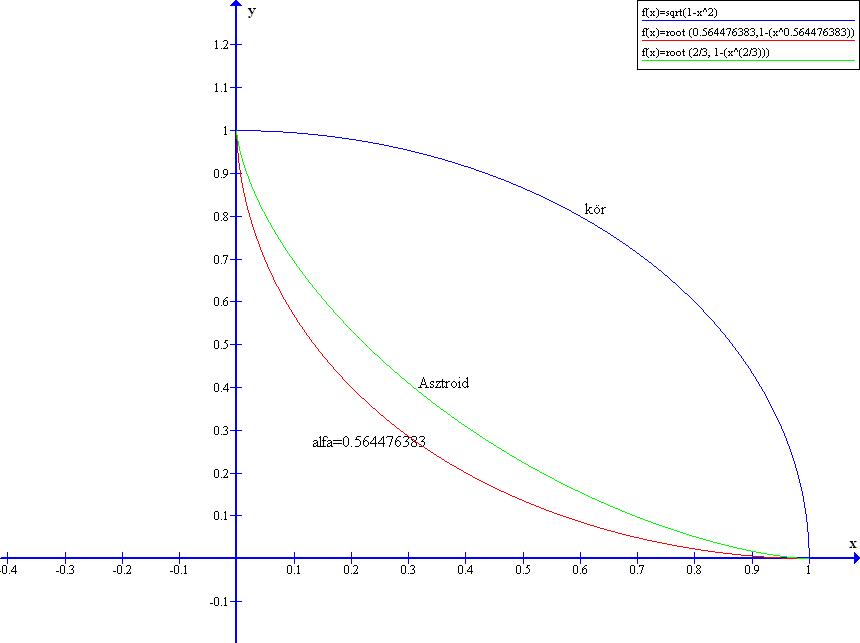

 2 értékek?
2 értékek?