|
|
| [1205] Lóczi Lajos | 2006-03-19 22:43:26 |
 Erről jut eszembe a következő
223. feladat. Számítsuk ki az
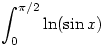
integrált.
|
|
|
| [1203] lorantfy | 2006-03-19 16:00:42 |
 222. feladat: Számítsuk ki a következő határozott integrál értékét:
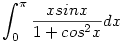
|
|
| [1202] lorantfy | 2006-03-19 15:55:20 |
 221. feladat: Oldjuk meg a p3+3p=7x+3 egyenletet, ahol p prímszám és az x egész szám.
(Műszaki főiskolák Hajós György matematika versenye 2003.)
|
|
| [1201] lgdt | 2006-03-18 20:27:57 |
 úgy látom, senkit sem hozott lázba a feladat, pedig érdekes. :-/ leírom a megoldást.
1. ki lehet nyírni, mert Zk (a k-dimenziós egész koordinátájú vektorok halmaza, ezek lehetnek a bolha stratégiái) és N között van egyértelmű megfeleltetés, és minden lövéssel ki tudunk zárni egy vektort, ha az n-edik másodpercben az n-edik vektor n-szeresére lövünk.
2. ki lehet nyírni, mert a stratégiák számegyeneséről az n-edik csapással egy 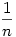 hosszúságú intervallumot zárunk ki, és hosszúságú intervallumot zárunk ki, és 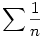 nem konvergens. nem konvergens.
3. megúszhatja, mert a stratégiák síkjáról az n-edik csapással egy  nagyságú területet zárunk ki, és nagyságú területet zárunk ki, és 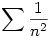 konvergens. konvergens.
|
| Előzmény: [1183] lgdt, 2006-03-10 19:19:16 |
|
|
|
|
| [1197] ágica | 2006-03-15 16:34:26 |
 :)
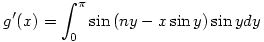
ez parciálisan integrálva:
![[-\cos{y}\sin{(ny-x\sin{y})}]_0^{\pi}+\int_0^{\pi}(n-x\cos{y})\cos{(ny-x\sin{y})}\cos{y}dy](keplet.cgi?k=D61818F66E3A6DE8)
itt az első tag nulla, a második tagot pedig felbonthatjuk két integrál különbségére:
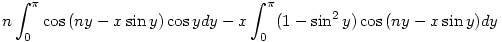
ennek második tagját még tovább bontva kapjuk:
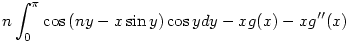
szorozzuk végig x-szel az egyenletet:

az integrálos tagról könnyen belátható, hogy n2g(x)-el egyenlő, ugyanis:
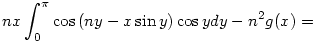
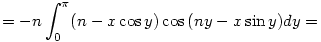
![=-n[\sin{(ny-x\sin{y})}]_0^{\pi}=0](keplet.cgi?k=7AA6A076AEE94EA3)
innen pedig már csak át kell rendezni.
Egyébként, lehet hogy hülye kérdés, de mi indokolta a Bessel-függvények definiálásakor azt az 1/ -s szorzót? (Mondjuk gondolom más "hasznuk" is van azon túl, hogy többek között ők is megoldják ezt a differenciálegyenletet.:) -s szorzót? (Mondjuk gondolom más "hasznuk" is van azon túl, hogy többek között ők is megoldják ezt a differenciálegyenletet.:)
|
| Előzmény: [1193] Lóczi Lajos, 2006-03-14 23:38:41 |
|
| [1196] qer | 2006-03-15 16:13:23 |
 219.feladatra:
Ez csak egy sejtés, de talán jó. k=1,2,3-ra (szerintem érdektelen) de nyílván jó a gömbfelület. k=4-re is a gömbfelület jön ki, elég egy tetraédert vizsgálni. k=5,6,... értékekre szerintem egy egyoldalú rendre 0,-2,... Euler-karakterisztikájú felület a megfelelő.
|
| Előzmény: [1187] Csimby, 2006-03-13 19:56:42 |
|
| [1195] qer | 2006-03-15 14:43:59 |
 218.feladatra: Először is legyen F egy tetszőleges felület, és  (F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy (F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy  (gömbfelület)=2. (gömbfelület)=2.
Ezután vizsgáljuk a körlap Euler-karakterisztikáját. Ez nyílván egy pontból, egy hurokélből és egy lapból áll, azaz  (körlap)=1-1+1=1.Az könnyen látható, hogyha egy gömbfelületből kivágunk egy körlapot, akkor egy másik körlap marad. (körlap)=1-1+1=1.Az könnyen látható, hogyha egy gömbfelületből kivágunk egy körlapot, akkor egy másik körlap marad.
Tórusz Euler karakterisztikáját (azaz k=1 esetre a kérdésre a választ) ugyanúgy számíthatjuk ki mint a körlapnál, azaz keresünk (egy lehetőleg minél egyszerűbb) felbontást. Vegyünk egy tóruszt, húzzunk be egy délkört, majd ottt vágjuk szét, de jegyezzük meg, hogy azok összetartoznak. Ha kiegyenesítjük, akkor egy hengerpalástot kapunk. Itt egy "magasság" mentén vágjuk szét a felületet, és ha kiegyenesítjük, akkor egy téglalapot kapunk, ahol a szemközti élek összetartoznak (azaz képzeletben összeragasztjuk őket). A két él egy pontban metszi egymást. Így  (tórusz)=1-2+1=0. (tórusz)=1-2+1=0.
Hogy meghatározhassuk más k-ra is az értéket, először is vegyünk egy tetszőleges F felületet, majd vágjunk ki belőle egy körlapot, vizsgáljuk, hogyan változik az Euler-karakterisztikája. Nyílván, ha egy lapot távolítunk (ami olyan mintha egy körlapot), akkor eggyel kevesebb lapja lesz az F felületnek, azaz l helyett l-1-et kell venni, azaz eggyel csökken az Euler-karakteriszika.
Ha két felület adott (mondjuk F és G), mindkettőből eltávolítunk egy-egy körlapot, majd a körlapon úgy veszünk fel csúcsokat, hogy mindkettőn ugyanannyi számú legyen (ez nyílván nem változtatja meg az Euler-karakterisztiká, mivel egy új ponttal egy új él is keletkezik), és a csúcsokat és az éleket összeragasztjuk, akkor a keletkező felület Euler-karakterisztikája egyenlő lesz  (F)+ (F)+ (G)-2-vel. (G)-2-vel.
Tórsuz úgy kapunk ha egy gömböt és tóruszt összeragasztunk, így  (k=1)=2+0-2=0 (persze ez nem újdonság,az eredmény az lett, amit vártunk). k=2 eset a k=1-re kapott felületből származik, ha még egy tóruszt ragasztunk hozzá, így (k=1)=2+0-2=0 (persze ez nem újdonság,az eredmény az lett, amit vártunk). k=2 eset a k=1-re kapott felületből származik, ha még egy tóruszt ragasztunk hozzá, így  (k=2)=0+0-2=(2+0-2)+0-2=2-2*(-2)=-2. Folytatva, tetszőleges k-ra, azt kapjuk, hogy (k=2)=0+0-2=(2+0-2)+0-2=2-2*(-2)=-2. Folytatva, tetszőleges k-ra, azt kapjuk, hogy  (k)=2-2k. (k)=2-2k.
|
 |
| Előzmény: [1187] Csimby, 2006-03-13 19:56:42 |
|
| [1194] Lóczi Lajos | 2006-03-14 23:58:40 |
 Valóban, úgy tűnik, Volterra csinált először ilyet Riemann integrálra (ami után persze adtak később egyszerűbb példákat is). A konstrukció lényege, hogy a korlátos derivált (mértékelméleti szempontból) túl sok helyen szakad: egy "kövér" Cantor-halmazon, az ilyeneket pedig Riemann nem tudja visszaintegrálni.
A feladatban viszont nem mondtam meg, milyen integrált használjunk.
220. feladat. U. az, mint a 217. feladat, csak az integrált értsük Lebesgue értelemben.
Ez a feladat jóval könnyebb, mint a Riemannos megfelelője, és az előzetes integrálos kérdések pont ezt készítették elő.
Fontos adalék, hogy Lebesgue (1900-as évek eleje) után fél évszázaddal kidolgozták a Henstock-Kurzweil integrált, amelynek definíciója formailag alig különbözik Riemannétól, és azzal a jó tulajdonsággal bír, hogy minden [a,b] intervallumon értelmezett deriváltat vissza tud integrálni (tehát a 217. feladatbeli formulában mindig egyenlőség áll), sőt egyúttal minden, [a,b]-n Lebesgue-integrálható függvényt is tartalmaz. Ezt az integrálfogalmat nyugodtan lehetne Riemann helyett tanítani, mert a bizonyítások csak alig bonyolultabbak és cserébe sokkal többet kapunk.
|
| Előzmény: [1191] nadorp, 2006-03-14 20:43:23 |
|
|
| [1192] ágica | 2006-03-14 22:50:28 |
 Vagy pedig, mivel g(x) csupán egy 1/ -s szorzóban különbözik az n-edik Bessel-függvénytől, melyre szintén teljesül ugyanez a differenciálegyenlet, így megoldható a feladat a Bessel-függvényekre vonatkozó bizonyítással teljesen analóg módon is (g(x) deriváltját számolva, majd parciálisan integrálva egy kis alakítgatás után kijön az egyenlet). -s szorzóban különbözik az n-edik Bessel-függvénytől, melyre szintén teljesül ugyanez a differenciálegyenlet, így megoldható a feladat a Bessel-függvényekre vonatkozó bizonyítással teljesen analóg módon is (g(x) deriváltját számolva, majd parciálisan integrálva egy kis alakítgatás után kijön az egyenlet).
|
| Előzmény: [1189] Lóczi Lajos, 2006-03-13 22:50:30 |
|
| [1191] nadorp | 2006-03-14 20:43:23 |
 Két helyen is találtam példát, mindkettő Volterra konstrukcióját közli. Azt látja be, hogy létezik olyan [0,1]-en mindenhol differenciálható függvény, melynek derivált függvénye korlátos, de nem Riemann integrálható.
|
| Előzmény: [1188] Lóczi Lajos, 2006-03-13 22:41:14 |
|
|
| [1189] Lóczi Lajos | 2006-03-13 22:50:30 |
 A deriválásokat elvégezve, ebben a feladatban nyilván csak annyit kell bizonyítani, hogy az y-szerinti integrálja 0-tól  -ig az alábbi kifejezésnek -ig az alábbi kifejezésnek
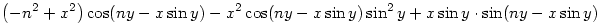
éppen nulla, ha n egész szám és x valós szám.
|
| Előzmény: [1184] Lóczi Lajos, 2006-03-10 23:10:59 |
|
| [1188] Lóczi Lajos | 2006-03-13 22:41:14 |
 Trükkös. Akkor a következő kérdés természetesen az, hogy
Van-e példa vajon olyan F függvényre, ami a zárt [0,1] intervallumon mindenhol értelmezve van, mindenhol deriválható, de az idézett Newton-Leibniz-formula nem igaz rá?
|
| Előzmény: [1186] ágica, 2006-03-13 19:39:06 |
|
| [1187] Csimby | 2006-03-13 19:56:42 |
 218. feladat Az Euler-féle poliéder-tétel ugyenbár csak "nem lyukas" testekre igaz. Hogy-néz ez ki "k lyukú testek" (k=1: tórusz, k=2: kengyel-felület) esetében?
219. feladat Adott a gömbön egy térkép országokkal és a fővárosaikkal. Vegyük azt a gráfot, aminek csúcsai a fővárosok, és két csúcsot pontosan akkor kötünk össze, ha a nekik megfelelő fővárosok országai határosak. Mondjunk olyan testet minden k-ra, hogy a testre lehessen olyan térképet rajzolni, amihez az előbbi módon definiált gráf a teljes k csúcsú gráf.
|
|
|
| [1185] Lóczi Lajos | 2006-03-12 01:59:04 |
 217. feladat. Adjunk példát (ha van) olyan F valós függvényre, amely deriválható az egész (0,1) intervallumon, de 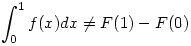 , ahol f=F'. , ahol f=F'.
|
|
| [1184] Lóczi Lajos | 2006-03-10 23:10:59 |
 216. feladat. Legyen n egész szám, x pedig valós szám. Igazoljuk, hogy az
x2g''(x)+xg'(x)+(x2-n2)g(x)=0
(differenciál)egyenlet egy megoldása a
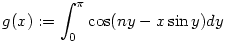 függvény. függvény.
|
|
| [1183] lgdt | 2006-03-10 19:19:16 |
 1. egy koordinátarendszerben egy láthatatlanul kicsi bolha minden másodperc elején mindig ugyanazzal az egész koordinátájú vektorral ugrik odébb (az origóból indul). tetszőleges egész koordinátájú pontjára lőhetsz minden másodperc végén.
2. a számegyenesen az origóból kiindulva mindig ugyanakkora valós számmal ugrik odébb. egy egységnyi szélességű vonalzóval csapkodhatsz minden ugrás után.
3. a síkon az origóból indulva mindig ugyanazzal a valós koordinátájú vektorral ugrik odébb, és egy négyzet alakú pecsét áll a rendelkezésedre.
Melyik esetben tudod kinyírni a bolhát és ha igen, hogyan?
Sorry a megfogalmazásért, valahogy így hangzott el előadáson is. Esetleg valaki átfogalmazhatná.
|
|
|
|
|
|
| [1178] Lóczi Lajos | 2006-03-08 21:20:15 |
 215. feladat. A kérdés ugyanaz, mint a 214-esben, csak az integrálokat ne improprius Riemann, hanem Lebesgue értelemben értsük.
|
|
|
|
| [1175] nadorp | 2006-03-08 16:17:05 |
 b) Az 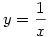 helyettesítéssel az integrál a következő alakú lesz helyettesítéssel az integrál a következő alakú lesz
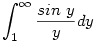 . Nyilván elég az . Nyilván elég az 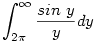 integrállal foglalkozni. Ezt a következőképpen érdemes felírni: integrállal foglalkozni. Ezt a következőképpen érdemes felírni:
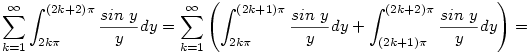
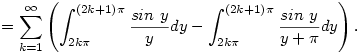
Innen már sejthető, hogy a fenti összeg becsülhető a 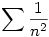 sorral, ami konvergens sorral, ami konvergens
|
| Előzmény: [1169] Lóczi Lajos, 2006-03-07 00:25:21 |
|
|
|
|
|
| [1170] jenei.attila | 2006-03-07 11:15:33 |
 Tényleg túl bonyolítod (vagy nem érted) a dolgot. Attól, hogy az együtthatók és p, q lehetnek negatívak is,ugyanúgy érvényesek Iván88 meggondolásai (van értelme negatív egészek paritásáról beszélni). Igen, negatív számok páratlan hatványa negatív, de akkor mi van? Össze tudunk adni pozitív és negatív számokat. A középső + jellel végképp nem értem mi bajod. Mennyiben más, ha a páratlan számot 2b-1 alakban írjuk fel, ugyanúgy 2b+1 alakban is megfelelő. Ne haragudj, de szerintem az ilyen hozzászólásod céltalan kötekedésnek minősíthető.
|
| Előzmény: [1168] hobbymatekos, 2006-03-07 00:02:07 |
|
| [1169] Lóczi Lajos | 2006-03-07 00:25:21 |
 214. feladat. Léteznek-e, és ha igen, végesek-e az alábbi integrálok?
a.) 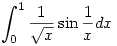
b.) 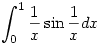
c.) 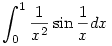
|
|
| [1168] hobbymatekos | 2006-03-07 00:02:07 |
 Csak arra gondoltam, még az nincs kihasználva, hogy p, q , és az együtthatók egész számok, azaz pozitiv és negativ számokat kellene összegezni, másrészt a negativ számok páratlan hatványai negativak, továbbá a két szumma közötti + jel az csupán a konstrukció következménye, hiszen (2b-1) alaku együtthatók is páratlan számok.
|
| Előzmény: [1167] jenei.attila, 2006-03-05 15:58:07 |
|
|
| [1166] hobbymatekos | 2006-03-04 12:40:13 |
 Szia.Szerintem: az indirekt feltevésed az volt p/q racionális és p,q relativ primek. Tehát azt kell megmutatni, hogy p/q komplex, irracionális vagy egész esetben (nem relativ primek) teljesülhet az utolsó (hibásan felirt) összeg.
|
| Előzmény: [1147] Iván88, 2005-12-31 23:50:08 |
|
| [1164] holusanyi | 2006-03-03 00:23:30 |
 Lenne egy feladat: elég érdekes szerintem, főleg mert nem tudtam megcsinálni! :) Az ötleteket e-mailben szivesen várom! 1 --> 4 --> 7 --> 9 --> 23 --> 47 --> 55 Milyen művelete(ke)t jelölnek a nyilak? Mindig ugyanaz! :)
|
|
|
|
| [1161] lorantfy | 2006-03-01 20:11:41 |
 Már másfél hónapja nem volt itt hozzászólás. Beírok egy példát, hátha érdekes lesz, azoknak akik nem ismerik:
213. feladat: A huszonhetedik dinasztia idején, amikor a repülőszőnyeg általános közlekedési eszköz volt, 7 repülőszőnyeg útvonal kötötte össze a a fővárost a birodalom többi városával. Az összes többi városból pontosan 4 repülőútvonal indult, kivéve a távoli Mesziút városát, ahonnan csak egy út indult. Mutassuk meg, hogy Messziút városából eljuthatunk a fővárosból repülőszőnyegen, esetleg más városokat érintve.
|
|
| [1160] xviktor | 2006-01-13 20:50:28 |
 Hali!
Nem olvastam el rendesen, azt hittem egesz egyutthatosrol van szo, amit irtam arra igaz. Masreszt a feladat szovege szerint van racionalis megoldas. Ha letezik, az csak a  1 lehet. 1 lehet.
Udv: Vik
|
| Előzmény: [1158] nadorp, 2006-01-13 19:33:18 |
|
|
| [1158] nadorp | 2006-01-13 19:33:18 |
 Egész együtthatósra valóban igaz, hogy ha van racionális gyök, akkor az 1 vagy -1 lehet. De a szimmetriával és azzal, hogy a -1 mindenképpen zéróhely, már baj van.
p(x)=x5+3x4+10x3-7x2-6x-1
p(1)=0, p(-1)=-10
|
|
|
|
| [1155] Iván88 | 2006-01-13 14:37:40 |
 Szia Viktor!
A válaszod jó, de nem egészen ez volt a kérdés.
Mivel a polinom fokszáma páratlan, és  x2a+1+... x2a+1+... 1 alakú, ezért valóban csak az 1 és a -1 lehet valós gyöke. A -1 mindenképpen az (hogy az 1 is, azt nem tudni), mert van valós gyöke. Értelemszerűen ekkor a -1 reciproka is gyöke az egyenletnek, ekkor viszont ez egy szimmetrikuspoéinom. (Amiből az is következik, hogy az első és utolsó tag előjele megegyezik) 1 alakú, ezért valóban csak az 1 és a -1 lehet valós gyöke. A -1 mindenképpen az (hogy az 1 is, azt nem tudni), mert van valós gyöke. Értelemszerűen ekkor a -1 reciproka is gyöke az egyenletnek, ekkor viszont ez egy szimmetrikuspoéinom. (Amiből az is következik, hogy az első és utolsó tag előjele megegyezik)
|
| Előzmény: [1152] xviktor, 2006-01-12 21:13:41 |
|
|
|
| [1152] xviktor | 2006-01-12 21:13:41 |
 Hali!
Horner-> ha van racionalis gyoke-> elso es utolso tag osztoinak hanyadosa lehet-> 1 lehet csak racionalis gyok. A tobbi lehet irracionalis vagy komplex... 1 lehet csak racionalis gyok. A tobbi lehet irracionalis vagy komplex...
Udv: Viktor
|
| Előzmény: [1151] Iván88, 2006-01-12 20:59:30 |
|
|
|
|
| [1148] Iván88 | 2006-01-12 19:30:23 |
 212. feladat:
Egy páratlan fokszámú polinom első és utolsó együtthatója  1. Mit állíthatunk a polinomról, ha van racionális gyöke? 1. Mit állíthatunk a polinomról, ha van racionális gyöke?
|
|
| [1147] Iván88 | 2005-12-31 23:50:08 |
 Sziasztok! Szép a feladat. Legyen a szóban forgó polin0m p(x). p(x)=a2nx2na2n-1x2n-1+...+a2x2+a1x+a0, ahol ai konstansok. Mivel ai páratlan, ezért ai=2bi+1 alakba hozható. (i=0;1;...;2n) Indirekt bizonyítás: Legyen x=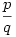 , ahol p,q (nem 0)egészek és relatív prímek. , ahol p,q (nem 0)egészek és relatív prímek. 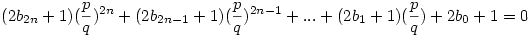 . Szorozzunk be q2n-nel: (2b2n+1)p2n+(2b2n-1+1)p2n-1q+...+(2b1+1)pq2n-1+(2b0+1)q2n=0. Ha kibontjuk a zárójeleket akkor azt kapjuk, hogy . Szorozzunk be q2n-nel: (2b2n+1)p2n+(2b2n-1+1)p2n-1q+...+(2b1+1)pq2n-1+(2b0+1)q2n=0. Ha kibontjuk a zárójeleket akkor azt kapjuk, hogy 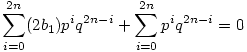 . Az első tag a 2-es szorzó miatt mindig páros. Nézzük a másodikat: p és q közül legfeljebb az egyik páros (mert relatív prímek) ekkor, ha p is, q is páratlan, akkor a második tag is páratlan, mivel 2n+1 értéket adtunk össze. Ha az egyig páros akkor is páratlan az összeg mert ekkor a második tagban 2n db. báros, és egy páratlan (amikor a páros szám a 0. hatványon szerepel, így az értéke 1) számot adtunk össze. Vagyis a második tag mindkét esetben páratlan, ekkor azonban az összegnek is páratlannak kell lennie, ami ellentmondás, mert a 0 egy páros szám. Azt kaptuk, hogy a racionális számok halmazán valóban nincs megoldás. Q.E.D. . Az első tag a 2-es szorzó miatt mindig páros. Nézzük a másodikat: p és q közül legfeljebb az egyik páros (mert relatív prímek) ekkor, ha p is, q is páratlan, akkor a második tag is páratlan, mivel 2n+1 értéket adtunk össze. Ha az egyig páros akkor is páratlan az összeg mert ekkor a második tagban 2n db. báros, és egy páratlan (amikor a páros szám a 0. hatványon szerepel, így az értéke 1) számot adtunk össze. Vagyis a második tag mindkét esetben páratlan, ekkor azonban az összegnek is páratlannak kell lennie, ami ellentmondás, mert a 0 egy páros szám. Azt kaptuk, hogy a racionális számok halmazán valóban nincs megoldás. Q.E.D.
|
| Előzmény: [1146] Csimby, 2005-12-10 23:37:29 |
|
| [1146] Csimby | 2005-12-10 23:37:29 |
 211. feladat Biz. be, hogy ha egy páros fokú polinom minden együtthatója páratlan egész, akkor a polinomnak nincsen racionális gyöke.
|
|
| [1145] Yegreg | 2005-12-06 17:35:29 |
 A feladat átfogalmazható úgy is, hogy a csoporton belülire vezető élek száma bármely csúcsnál legfeljebb egy.
Oszzuk két csoportba a csúcsokat tetszőlegesen! Ha a kívánt elrendezés lép fel, akkor készen vagyunk, ha nem, akkor van olyan csúcs, amelyből a saját csoportjába vezető élek száma legalább kettő, ez azt jelenti, hogy a másik csoportba vezető él(ek :)) száma legfeljebb egy, hiszem minden pont foka legfeljebb három. Ekkor a következőt tesszük: ezt a csúcsot áthelyezzük a másik halmazba. Ezzel ezen csúcs korábbi csoportjában legalább 2-vel csökkent, új csoportjában pedig legfeljebb 1-gyel nőtt a csoporton belüli összes él száma, ez azt jelenti, hogy ez a lépés csökkenti a két csoport összes csoporton belüli éleinek számát.
Ha ezzel a lépéssel a kívánt helyzethez jutunk, akkor kész, ha nem, akkor folytatjuk az eljárást.
Mivel az eljárások során a két csoport összes csoporton belüli éleinek száma szigorúan monoton csökken, és ha nem a kívánt helyzet áll fennt, akkor biztosan folytathatjuk az eljárást, ezért következik, hogy egyszer biztosan véget ér, hiszen az két csoport összes csoporton belüli éleinek száma természetes szám mindig, és pl. 0-nál triviálisan a kívánt helyzet alakul ki.
Ennek a feladatnak viccesebb változata, amikor a politikusok vágják pofon egymást...:)
Üdv:
Szűcs Gergely
|
|
| [1144] Csimby | 2005-12-05 16:16:32 |
 210. feladat Bizonyítsuk be, hogy ha egy gráfban minden pont foka legfeljebb 3, akkor a gráf csúcsai két részre oszthatóak úgy, hogy ha a két rész között menő éleket töröljük, minden pont foka legfeljebb 1 lesz.
|
|
|
|
|
| [1140] jonas | 2005-11-28 19:42:12 |
 Van pár diszkrét matek feladatom. Feladom őket itt, hátha valakit érdekel.
209. Legyen s0=0; s1,P,Q tetszőleges egészek. Definiáljuk az sn sorozatot az sn+1=Psn-1+Qsn rekurzióval.
Lássuk be, hogy ekkor minden n,k egészre
(sn,sk)=s(n,k)
ahol (n,k) jelöli a két szám legnagyobb közös osztóját. Speciális esetként sk osztója sn-nek akkor és csak akkor, ha k osztja n-et.
Érdemes megnézni, milyen sorozatokat kapunk s1=P=Q=1 illetve az s1=1,P=-2,Q=3 esetén.
A másik két feladatot majd később feladom, ha van érdeklődés (a nevek a másodikban Catalan és Hankel, a harmadikban Catalan és Csebisev).
|
|
| [1139] Lóczi Lajos | 2005-11-17 19:30:54 |
 208. feladat. Adjunk példát olyan (pontosan) elsőfokú egyenletre, aminek nincs megoldása a kvaterniók között.
|
|
| [1138] Lóczi Lajos | 2005-11-17 19:16:27 |
 Igen, itt is az 1/2 bukkant fel. (De a legjobban arra lennék kíváncsi, hogy ennek vajon van-e bármiféle köze ahhoz az eredményhez, ami az "ujjgyakorlatok" 88-as feladatában fog kijönni: "szimmetria és extrémum" egybeesése, amire más helyeken is sok példát láttam már...)
|
| Előzmény: [1137] nadorp, 2005-11-17 11:43:02 |
|
| [1137] nadorp | 2005-11-17 11:43:02 |
 Biztos van elemibb megoldás is,ez a következőt használja:
Ha 0<x<1, akkor nyilván
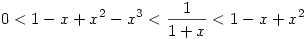 ,azaz mindkét oldalt 0-tól x-ig integrálva ,azaz mindkét oldalt 0-tól x-ig integrálva
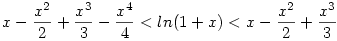
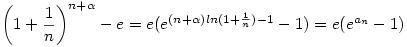 . Mivel az ex függvény szigorúan monoton nő,a 0-ba történő konvergencia sebességét nyilván az dönti el, hogy an milyen gyorsan tart nullába. . Mivel az ex függvény szigorúan monoton nő,a 0-ba történő konvergencia sebességét nyilván az dönti el, hogy an milyen gyorsan tart nullába.
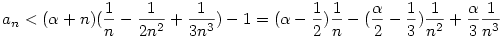 . .
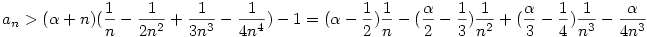 . .
Látszik, hogy ha 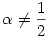 ,akkor ,akkor 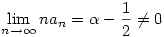 ,azaz an konvergenciájának nagyságrendje ,azaz an konvergenciájának nagyságrendje 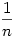 , ,
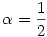 esetén pedig esetén pedig 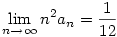 ,azaz an konvergenciájának nagyságrendje ,azaz an konvergenciájának nagyságrendje 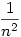 és ez gyorsabb. és ez gyorsabb.
|
| Előzmény: [1133] Lóczi Lajos, 2005-11-16 12:19:00 |
|
|
|
| [1134] Sirpi | 2005-11-16 12:57:54 |
 Ezt a problémát már régebben én is kitaláltam. Én úgy oldottam meg, hogy definiáltam a következő xn sorozatot: 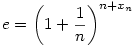
Ekkor az xn sorozat konvergens, és a határértékét nem mondom meg egyelőre :-)
Bár úgy érzem, a kétféle megközelítés ugyanarra az eredményre vezet, de be kéne látni, hogy ez tényleg így is van.
|
| Előzmény: [1133] Lóczi Lajos, 2005-11-16 12:19:00 |
|
|
|
|
|
|
|
| [1127] Lóczi Lajos | 2005-11-14 19:31:31 |
 Ami alatt azt érted nyilván, hogy az ember ilyenekkel nem sokra megy, hiszen az egyik végtelen szorzatot átkonvertálja egy ki nem számítható integrálba, illetve végtelen összegbe. :)
Inkább érdekesebbek pl. a becslések. Hagyjuk el a gyököt az egyszerűség kedvéért. Egy lehetséges approximáció, pl. 5-nél kettébontva:
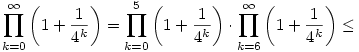
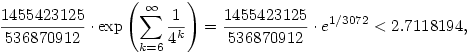
felhasználva, hogy 1+x ex minden valós x-re, továbbá a mértani sor összegképletét. ex minden valós x-re, továbbá a mértani sor összegképletét.
Egy alsó becslés pl.
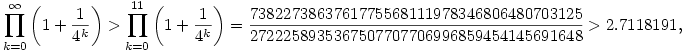
használva a monoton növekedést.
|
| Előzmény: [1125] Róbert Gida, 2005-11-14 16:50:59 |
|
| [1125] Róbert Gida | 2005-11-14 16:50:59 |
 Zsabóka végtelen szorzatos feladatához: Nyilván elég i=1-től menni és a négyzetét vizsgálni, mert ha ez megvan, akkor könnyen megkapható az eredeti szorzat is. De ez éppen http://mathworld.wolfram.com/InfiniteProduct.html oldalon található 43. formula spec. esete n=4-re. Nem tudom erre gondoltál-e. Nem a legszebb formula.
|
|
| [1124] nadorp | 2005-11-14 14:33:37 |
 Ezt sajnos elszámoltam, pontosabban az elv volt rossz.Ez a feladat összefügg a számok partícióinak a számával, én meg sajnos csak a kéttagú partíciókat vettem.A végeredmény az enyémnél több lesz.
|
| Előzmény: [1123] Zsabóka, 2005-11-14 13:34:46 |
|
| [1123] Zsabóka | 2005-11-14 13:34:46 |
 Itt aztán gyorsan lebukik az ember -), hiba került a feladatba. Igazából:
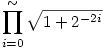
lett volna a feladat. Ettöl perzse semmi nem lett könnyebb. De hogy jutottál az
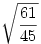
alakra ? Ez alapján az eredmény
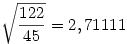
lenne.
|
| Előzmény: [1122] nadorp, 2005-11-14 13:17:59 |
|
|
|
| [1120] Zsabóka | 2005-11-14 12:20:17 |
 Keresett a következö szorzat értéke:
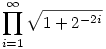
Van esetleg valami köze PI-hez, e-hez ( a négyzete majdnem e )?
|
|
|
| [1118] lorantfy | 2005-11-13 17:25:49 |
  i, i, j, j, k-n kívül van még megoldás? k-n kívül van még megoldás?
Én már majdnem elfelejtettem mik ezek a kvaterniók, így hála Neked, most utána néztem.
A komlex számfogalom 4 dimes kiterjesztéséről van szó:
Ferde testekre ( ferde az olyan test, melyben a szorzás nem kommutatív ) az egyik legfontosabb példa a kvaterniók teste.
Az a+ib+jc+kd alakú kifejezéseket kvaternióknak nevezzük, ahol a,b,c,d tetszőleges valós számokat jelölnek az i,j,k szimbólumokra pedig teljesülnek az alábbi azonosságok
(I) i2=j2=k2=-1,
(II) ij=k, jk=i, ki=j, ji=-k, kj=-i, ik=-j.
Kvaterniókra az összeadást az alábbi egyenlőség definiálja:
(a+ib+jc+kd)+(a`+ib`+jc`+kd`)=(a+a`)+i(b+b`)+j(c+c`)+k(d+d`).
A szorzást úgy végezzük el mint ahogy több tagot szokás többtaggal szorozni, figyelembe véve a (I),(II)-ben szereplő azonosságokat. Test axiómák teljesülése könnyen igazolható. A multiplikatív inverz létezésének igazolása sem nehéz, ha figyelembe vesszük, hogy:
(a+ib+jc+kd)[a+i(-b)+j(-c)+k(-d)]=a2+b2+c2+d2.
|
| Előzmény: [1116] Lóczi Lajos, 2005-11-13 14:24:37 |
|
| [1117] Lóczi Lajos | 2005-11-13 16:09:14 |
 206. feladat. Keressük meg mindazokat a q=a+bi+cj+dk egész kvaterniókat (ahol tehát a,b,c,d valós egészek), melyekre
(2+3i+5j+7k)q=q(2+3i+5j+7k)
teljesül. (Szokás szerint i,j,k jelöli a kvaterniók báziselemeit.)
|
|
| [1116] Lóczi Lajos | 2005-11-13 14:24:37 |
 205. feladat. Oldjuk meg a kvaterniók körében a
q2+1=0
egyenletet!
|
|
| [1115] Lóczi Lajos | 2005-11-13 14:07:37 |
 Egy régi feladat átfogalmazása következzen:
204. feladat. Jelölje a komplex számok alábbi részhalmazát
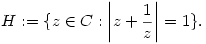
Mutassuk meg, hogy H korlátos. Adjuk meg továbbá azt az origó középpontú körgyűrűt, amely befedi a H halmazt és területe minimális.
|
|
| [1114] Lóczi Lajos | 2005-11-04 21:55:36 |
 203. feladat. Tekintsük a síkon azt a paraméteres görbét, amelyet a
t (2t-sin t,2t+cos t) (2t-sin t,2t+cos t)
hozzárendelés értelmez, ha t [0, [0, ]. Van-e ennek a görbének inflexiós pontja (azaz olyan görbepont, amelyben a görbe érintője "átmetszi" a görbét)? Ha igen, hol? ]. Van-e ennek a görbének inflexiós pontja (azaz olyan görbepont, amelyben a görbe érintője "átmetszi" a görbét)? Ha igen, hol?
|
|
|
| [1112] lorantfy | 2005-11-03 11:53:11 |
 Már indítanám a programot, hogy megkeressem a többi megoldást, de sajnos Pascalban a longint csak 2 milliárdig bírja, így reménytelen a helyzet! :-)
Azért elég jól megmozgatta az emberek fantáziáját ez a feladat. Vagy 50 hozzászólás jött, ami ezzel kapcsolatos.
A Fermat könyv csak ezt az egy ellenpéldát említi az Euler sejtés cáfolataként.
|
| Előzmény: [1110] Lóczi Lajos, 2005-11-02 20:23:27 |
|
| [1111] lorantfy | 2005-11-03 11:36:16 |
 Kedves Lajos!
A megoldásod rendben van. Az én hibám, hogy a feladat kitűzésénél nem fogalmaztam meg, hogy a megoldásnak a sakkal való kapcsolatát keressük.
Írjuk át az egyenletrendszert 2 dimes vektoregyenletre:
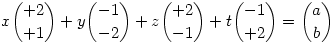
Egy végtelen sakktáblán a (0,0) mezőről el kell jutnunk az (a,b) pontba lólépésben.
|
| Előzmény: [1108] Lóczi Lajos, 2005-11-02 20:15:53 |
|
|
|
| [1108] Lóczi Lajos | 2005-11-02 20:15:53 |
 Nem értem.
"Két egyenletünk van és 4 ismeretlen. Hát miért is ne lenne egész megoldás!"
Íme, egy példa, amikor 1 egyenlet és 4 ismeretlen van, mégsincs megoldás:
2x+2y+2z=2t+1.
Az általam felírt megoldások ekvivalensek az eredeti rendszerrel, tehát annak összes megoldása előállítható a megadott képlettel.
De most már én is kíváncsi vagyok a sakk-kapcsolatra :)
|
| Előzmény: [1107] lorantfy, 2005-11-02 17:03:04 |
|
| [1107] lorantfy | 2005-11-02 17:03:04 |
 Két egyenletünk van és 4 ismeretlen. Hát miért is ne lenne egész megoldás! Nyugodtan megtehetjük, hogy egyik változót lefixáljuk, még akkor is mindig van egész megoldás a többire.
Végülis az az érdekesség benne, ha rájövünk, mi az összefüggés a feladat és a sakk között.
Káli gúlának sikerült! Grat!
|
| Előzmény: [1104] Lóczi Lajos, 2005-11-01 22:43:28 |
|
|
| [1105] Káli gúla | 2005-11-01 23:26:25 |
 Adjuk össze és vonjuk ki egymásból a 2 egyenletet:
3(x-y)+(z+t)=a+b
(x+y)+3(z-t)=a-b
A zárójeles összegek helyére írjunk A,B,C,D-t:
3A+B=a+b
C+3D=a-b
Ilyen A,B,C,D nyilván van, mert 1 és 3 relatív prímek. Azt kell biztosítani, hogy itt A=C és B=D (mod 2) legyenek, pl. úgy, hogy legyen A=a+b (mod 2) és C=a-b (mod 2)
|
| Előzmény: [1100] lorantfy, 2005-10-30 21:49:05 |
|
| [1104] Lóczi Lajos | 2005-11-01 22:43:28 |
 Legyenek a, b és t tetszőleges egészek. Ekkor
x:=-a-2b-2t, y:=-a-2b-t, z:=a+b+2t
megoldás. Sőt, általánosabban
x:=-a-2b-2t+5w, y:=-a-2b-t+4w, z:=a+b+2t-3w
is megoldás, ha w tetszőleges egész.
|
| Előzmény: [1100] lorantfy, 2005-10-30 21:49:05 |
|
|
|
|
| [1100] lorantfy | 2005-10-30 21:49:05 |
 202. feladat: Bbh. hogy az alábbi egyenletrenszernek minden a,b Z esetén van x,y,z,t Z esetén van x,y,z,t Z megoldása! Z megoldása!
2x-y+2z-t=a
x-2y-z+2t=b
|
|
| [1099] medvecukor | 2005-10-25 21:06:29 |
 KÖSZÖNÖM SZÉPEN!:)
örök hálám,köszönöm mindenki segítségét:)
utólag nem is olyan nehéz:)
|
|
| [1098] xviktor | 2005-10-25 00:44:53 |
 Elnezest kerek, valoban elneztem. ZH-ra keszulve az n-dimenzios paralelepipedon elojeles terfogata es a komplex szamok kozott, egy kisse osszecsptam a megoldast. Koszonom, hogy eszrevettek a hibat.
Udv: Viktor
|
| Előzmény: [1094] lorantfy, 2005-10-25 00:03:35 |
|
|
|
|
|
|
|
| [1091] Lóczi Lajos | 2005-10-24 22:46:41 |
 Nekem más jött ki, az első esetben én a kúpot az alapján fekvőnek vettem, más jelölésekkel ekkor
a víz aljánál az eredeti kúp sugara legyen R, a víz tetejénél a kúp sugara r, a víz magassága x. Ekkor hasonló háromszögekből r=R(24-x)/24.
A fordított szituációban a nagykúp a csúcsán áll, a víz tetejénél a kúpsugár legyen  , ami =R.(2x)/24. Persze R itt is az eredeti kúp sugara. , ami =R.(2x)/24. Persze R itt is az eredeti kúp sugara.
A víz térfogata azonos a két esetben, azaz
R2 /3.24-r2 /3.24-r2 /3(24-x)= /3(24-x)= 2 2 /3.2x. /3.2x.
Ezt x-re megoldva 3 megoldás adódik: 0 illetve
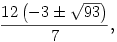
ahol csak a "+" jöhet szóba, ami kb. 11.3891.
|
|
| [1090] xviktor | 2005-10-24 22:29:34 |
 Szia!
A kup magassaga legyen M. A kiskup magassaga 2m, a csonkakup magassaga m. A kis kup alapkorenek sugara r1, a csonkakup fedokorenek sugara r2, alapkorenek sugara r3. Irjuk fel a terfogatokat:
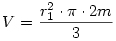 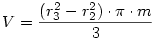
Mivel a viz terfogata nem valtozik: 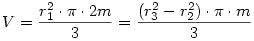
(1) Ebbol kapjuk, hogy: r32-r22=2.r12
Megfigyelheto, hogy kupok hasonlosaga miatt:  . .
A fentibol kijon, hogy: 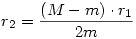 , , 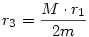 , amit behelyettesitunk az (1)es egyenletbe: , amit behelyettesitunk az (1)es egyenletbe:
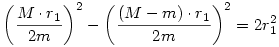
Ebbol ha minden igaz kijon r12 kiesese utan egy elsofoku egyenlet m-re: 9m-48=0, amibol m 5,33cm jon ki. 5,33cm jon ki.
Remelem nem szamoltam el semmit, azert erdemes megegyszer atszamolnod.
Udv: Viktor
|
| Előzmény: [1089] medvecukor, 2005-10-24 21:54:52 |
|
| [1089] medvecukor | 2005-10-24 21:54:52 |
 Sziasztok, van egy matekfeladat, amin 1.5 órát törtem a fejemet de szinte sehova se jutottam, légyszi segítsetek megoldani!
4.6) Egy egyenes körkúp alakú, m=24 cm magasságú zárt edényben víz van. Ha a kúpot "fejre" állítjuk, akkor kétszer olyan magasan áll a víz a kúpban. Milyen magasan állt a víz a kúpban eredetileg?
Ez egy feladat az "Egyenes út az egyetemre" című kötetből.
Segítségeteket előre is köszönöm: medvecukor
|
|
| [1088] qer | 2005-10-19 23:19:36 |
 Akkor talán egy harmadik megoldás:
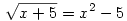
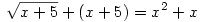
Az egyszerűség kedvéért legyen 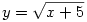 . Ekkor: . Ekkor:
y2+y=x2+x
x2-y2+x-y=0
(x-y)(x+y)+(x-y)=0
(x-y)(x+y+1)=0
Innen már csak két másodfokú egyenlet meg ha nem tettél kikötést akkor gyökvizsgálat...
|
| Előzmény: [1081] philip, 2005-10-19 17:44:52 |
|
| [1087] nadorp | 2005-10-19 22:54:01 |
 Ha 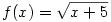 és g(x)=x2-5, akkor az f(x)=g(x) egyenletet kell megoldani.Ekkor és g(x)=x2-5, akkor az f(x)=g(x) egyenletet kell megoldani.Ekkor
g(f(x))=g(g(x) is teljesül. De g(f(x))=x, ezért
g(g(x))=x
Ha g(x)=x, akkor g(g(x))=x is teljesül, ezért az x2-5=x egyenlet gyökei az eredetinek is gyökei, azaz x2-x-5 a Csimby által említett egyik tényező.
|
| Előzmény: [1081] philip, 2005-10-19 17:44:52 |
|
|
| [1085] Csimby | 2005-10-19 21:08:00 |
 A lényeg, hogy valahogy kitalálod a szorzattá bontást:
x4-10x2-x+20=(x2-x-5)(x2+x-4)
És mivel a szorzat akkor 0, ha valamelyik tényező 0, ezért elég ezt a két másodfokú egyenletet megoldanod.
|
| Előzmény: [1084] philip, 2005-10-19 20:53:44 |
|
| [1084] philip | 2005-10-19 20:53:44 |
 esetleg nincsen valami ojan megoldási lehetőség,amit 10dikes fejjel meglehet csinálni.....ugyanis nemigazán vettünk minden ojan anyagot,ami az általad leírt megoldásban szerepel.....
|
|
|
| [1082] Csimby | 2005-10-19 19:20:29 |
 Négyzetre emeljük mindkét oldalt és egy oldalra rendezzük:
f(x)=x4-10x2-x+20=0
Próbáljuk meg két másodfokú szorzatára bontani (mindkét tényezőben a főegyüttható 1, hiszen a szorzat főegyütthatója a tényezők főegyütthatójának szorzata):
(x2+ax+b)(x2+cx+d)
Végezzük el a szorzást! Két polinom akkor egyenlő, ha az együtthatóik egyenlőek, tehát az alábbi egyenleteket írhatjuk fel:
0=a+c
-10=d+b+ac
-1=ad+cb
20=db
A Második Gauss Lemma szerint ha f egész együtthatós polinomot felbontottuk a racionális együtthatós g és h polinomok szorzatára, akkor g és h megszorozható alkalmas racionális számokkal úgy, hogy a kapott g0 és h0 polinomok egész együtthatósak legyenek és f=g0h0 teljesüljön.
Ezért tehettük föl, hogy h és g főegyütthatója 1 (vagy asszociáltja) és kereshetjük a kapott egyenletrendszer megoldását az egész számok körében. Amit innentől szerintem be tudsz fejezni.
Ha kijöttek az együtthatók, megoldod a két másodfokú egyenletet a megoldóképlettel, így 4 gyököt fogsz kapni. De 2 gyök nem elégíti ki az eredeti egyenletet, hiszen ott a bal oldal pozitív -> a jobboldal is pozitív -> 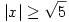
|
| Előzmény: [1081] philip, 2005-10-19 17:44:52 |
|
| [1081] philip | 2005-10-19 17:44:52 |
 Sziasztok!Lehet ,hogy nem az érdekes feladatok közé tartozik,de segítség kellene ennek az egyenletnek a megoldásában...A segítséget előre is köszönöm!
|
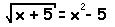 |
|
|
|
| [1078] Sirpi | 2005-10-18 10:29:55 |
 Na, ez a feladat nagyon tetszett, nem hallottam még korábban, csak mindenféle elcsépelt egyféle bábos felpakolásokat.
8x8-asra k=5, 10x10-re k=7 (tovább még nem volt időm vizsgálódni), mindkettőre van konstrukcióm, és könnyű látni, hogy többet nem lehet felrakni. Utóbbinak leírom a bizonyítását, ábrát egyelőre nem teszek fel.
Szóval ha egy nxn-es sakktáblára fel lehet tenni k db bástyát és futót egyszerre, akkor teljesülnie kell az (n-k)2 k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2 k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2 k, ahonnan viszont adódik, hogy k, ahonnan viszont adódik, hogy 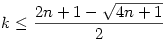 , ez pedig n=8-ra , ez pedig n=8-ra 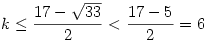 , tehát ekkor k<6, vagyis k , tehát ekkor k<6, vagyis k 5. Hasonlóan adódik n=10-re, hogy k 5. Hasonlóan adódik n=10-re, hogy k 7. 7.
Ez utóbbi nehezebb különben, mert míg 8-ra 5 db futónak kell elférnie egy 3x3-as területen, addig 10-re ugyanígy egy 3x3-as részre 7 futót kell bepréselni.
|
| Előzmény: [1073] rizsesz, 2005-10-17 00:28:27 |
|
|
|
|
| [1073] rizsesz | 2005-10-17 00:28:27 |
 201. feladat.
Adott egy 8*8-as sakktábla, és a k pozitív egész. Mekkora k maximális értéke, ha létezik hozzá olyan elrendezése k darab futónak és k darab bástyának egyazon sakktáblán, hogy egyik bábu sem üti a másikat?
|
|
| [1072] Lóczi Lajos | 2005-10-16 23:36:48 |
 200. feladat. Adjuk meg azt a p valós számot, amelyre az
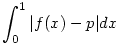
integrál értéke minimális, ha
f(x)=1-e-x2.
|
|
| [1071] jonas | 2005-09-14 21:38:33 |
 Ezt véletlenül ismerem, mert egyszer javítottam a megoldásait.
a: Nem.
b: Csak a c3, f3, c6, f6 mezők valamelyikét hagyhatjuk el.
Három színnel átlósan kell színezni a sakktáblát (vagy lehet nem átlósan, hanem soronként is, úgy, hogy minden dominó alatt hárommal osztható összeg álljon).
|
| Előzmény: [1065] Csimby, 2005-09-14 00:03:02 |
|
|
|
|
| [1067] nadorp | 2005-09-14 16:45:54 |
 Lehet, hogy félreérthető a megfogalmazás:
a ... tört részt jelent.
|
|
| [1066] nadorp | 2005-09-14 16:19:56 |
 Szia Rizsesz !
A b) verziót szerintem a következőképpen lehetne értelmezni:
Legyenek n és k pozitív egészek és legyen
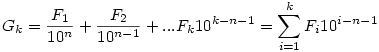
Bizonyítsuk be, hogy létezik egy olyan n pozitív egész és egy k1<k2<... indexsorozat, hogy a
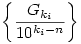 sorozat konvergens és határértéke egy prím reciproka. sorozat konvergens és határértéke egy prím reciproka.
|
| Előzmény: [1060] rizsesz, 2005-09-11 16:52:33 |
|
| [1065] Csimby | 2005-09-14 00:03:02 |
 199.feladat A 8×8-as sakktábla egyik sarkából kivágunk egy 1×1-es négyzetet.
a. Lefedhető-e a megmaradt sakktábla 3×1-es téglalapokkal?
b. Ha a teljes sakktáblából akárhonnan kivághatunk egy 1×1-es négyzetet, honnan tegyük ezt meg ahhoz, hogy a megmaradt tábla lefedhető legyen 3×1-es téglalapokkal?
|
|
| [1064] Sirpi | 2005-09-13 15:44:55 |
 198. feladat: Mely pozitív egészek egyeznek meg 4 legkisebb pozitív osztójuk négyzetösszegével? Mi a helyzet 4 helyett 3-ra?
|
|
|
| [1062] jonas | 2005-09-12 21:42:51 |
 Szerintem igen.
Ugyanis a polinom deriváltja is polinom, tehát folytonos, tehát lokálisan korlátos változású, tehát felírható két monoton növő függvény különbségeként. Ezeket tagonként határozatlanul integráljuk (a konstansra is vigyázva), és megkapjuk a polinomot két konvex függvény különbségeként.
|
| Előzmény: [1061] Káli gúla, 2005-09-12 20:54:13 |
|
|
| [1060] rizsesz | 2005-09-11 16:52:33 |
 Kedves Lorantfy! A tesztversenyen volt az a Fibonacci számos feladat. annak van egy b., verziója, amibe még régebben ütköztem bele, de valahogy nem volt se füle, se farka :) Az a feladat, hogyha a Fibonacci sorozat elemeit egy-egy tizedeshellyel eltolva (akár balról jobbra, akár jobbról balra haladva) egymás alá írjuk és összeadjuk, akkor a sok szám összege végül ismétlődő szakaszokból fog állni, tehát olyan lesz, mint a végtelen szakaszos tizedestörtek. Sőt, nem csak olyan, hanem az is! Ha megfelelő helyre tesszük a tizedesvesszőt, akkor a két összeg éppen 1/A, illetve 1/B értékű lesz, ahol A és B prímszámok. Mennyi A értéke, ha jobbra tolva írjuk egymás alá az elemeket és mennyi B értéke, ha balra? A balra irány így néz ki valahogy:
00001
0001
002
03
5
|
| Előzmény: [1050] lorantfy, 2005-09-02 16:35:32 |
|
| [1059] Lóczi Lajos | 2005-09-10 23:51:47 |
 197. feladat. Legyenek f és g az egész számegyenesen értelmezett konvex függvények, amelyek semelyik intervallumon sem esnek egybe. Legfeljebb hány megoldása lehet az f(x)=g(x) egyenletnek?
|
|
| [1058] qer | 2005-09-10 14:15:30 |
 Ez adta az ötletet: Bármely poliéderbe beirt gömb sugara: 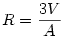 . Picit átrendezve: . Picit átrendezve: 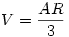 . .
Van egy ehhez hasonló tétel a síkban is: Egy kör köré írt sokszög területe feleakkora, mint a sokszög kerületének és a kör sugarának a szorzata. Azaz: 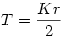 . .
Az analóg n dimenziós tételek igazak-e?
|
| Előzmény: [1010] xviktor, 2005-08-13 01:19:00 |
|
| [1057] Lóczi Lajos | 2005-09-05 22:24:07 |
 Az ilyen típusú feladatoknál jól használható az alábbi azonosság (a megfelelő értelmezési tartományok figyelembe vételével):
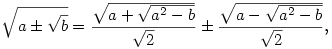
tehát ha a2-b négyzetszám, a dupla gyök mindig kiküszöbölhető.
|
| Előzmény: [1056] Csimby, 2005-09-05 20:53:00 |
|
| [1056] Csimby | 2005-09-05 20:53:00 |
 196. feladat: Állítsuk elő két négyzetgyök összegeként:
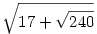
|
|
|
| [1054] CsG | 2005-09-04 12:33:54 |
 195.feladat:
Adott egy körben két egyenlő hosszú húr, ezeknek egyik végpontja közös. Milyen feltételnek kell teljesülnie a húrok által bezárt szögre ha a körben egynél több olyan húr létezik, amelyet az adott húrok három egyenlő részre osztanak?
|
|
| [1053] lorantfy | 2005-09-04 11:53:17 |
 A B. 3719. kitűzött feladatnak is ez volt a lényege. 2004. márciusában volt.
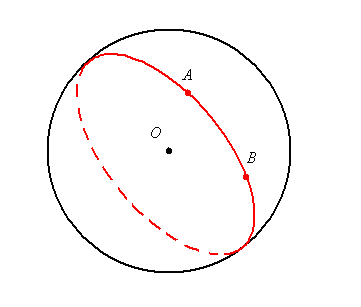
Három pontnál: Ha mindhárom pont egybeesik akkor egy félgömbön vannak. Ha A és B pontok nem esnek egybe, akkor tekintsük az O ( gömb középpontú) A-t és B-t is tartalmazó főkört. C pont eshet a főkörre, az egyik félgömbre vagy a másik félgömbre, a három pont mindenképpen egy zárt félgömbön van.
A kitűzött példában 5 pontról volt szó. Az A és B ponton kívül még 3 pontot kell elhelyezni a gömb felszinén. Az egybeeső esetektől eltekintve a 3-ból 2-nek azonos félgömbön kell lennie, így 4 pont mindig azonos zárt félgömbre esik.
|
 |
| Előzmény: [1051] Peti123, 2005-09-03 21:18:43 |
|
|
| [1051] Peti123 | 2005-09-03 21:18:43 |
 194. feladat:
Egy gömb felületén véletlenszerűen kiválasztunk három pontot. Mennyi a valószínűsége, hogy a választott pontok ugyanazon a félgömbön helyezkednek el?
|
|
|
| [1049] rizsesz | 2005-09-01 19:00:09 |
 http://www.komal.hu/verseny/1999-10/B.h.shtml , itt a B. 3304. sorszám alatt található a feladat az 1, 2... 12 esetben.
|
|
| [1048] lorantfy | 2005-09-01 16:19:22 |
 Szia Viktor!
Ez a megoldás! De az utolsó mondatod megfogalmazása kicsit szerencsétlen :-)!
Igy ha az élekre írt egymás után következő 12 természetes szám összegének kétszeresét 8 egyenlő részre osztjuk, akkor nem kaphatunk egész számot.
|
| Előzmény: [1045] xviktor, 2005-09-01 15:50:07 |
|
| [1047] xviktor | 2005-09-01 16:15:30 |
 Bocsesz. Csak a feladatot neztem, Sirpi megoldasat nem :S
|
|
|
| [1045] xviktor | 2005-09-01 15:50:07 |
 193. feladat: Vegyuk a termeszetes szamokat: n, n+1,...n+11 Mindegyik el ket csucsba megy, igy a 8 csucson levo szamok osszege az eleken levo szamok osszegenek ketszerese: ![2\cdot\left[n+(n+1)+...+(n+11)\right]=2\cdot\frac{n+(n+11)}{2}\cdot12=(2n+11)\cdot12](keplet.cgi?k=38DB592112677ECF) A zarojelben levo szam minden n-re paratlan, igy nem oszthato kettovel. 12-nek nem osztoja 8, csak 4. Igy ha 12 egymas utani termeszetes szamokat irnank az elekre, akkor minden csucson k,5 alapu szamnak kene lennie, de ez ellentmondas, hiszen barmely 3 termeszetes szam osszege egesz. A zarojelben levo szam minden n-re paratlan, igy nem oszthato kettovel. 12-nek nem osztoja 8, csak 4. Igy ha 12 egymas utani termeszetes szamokat irnank az elekre, akkor minden csucson k,5 alapu szamnak kene lennie, de ez ellentmondas, hiszen barmely 3 termeszetes szam osszege egesz.
Szerintem ez a megoldas: Viktor
|
| Előzmény: [1043] lorantfy, 2005-09-01 11:37:07 |
|
| [1044] Sirpi | 2005-09-01 13:07:36 |
 12 egymás utáni szám összege nem osztható 4-gyel, mert ha a kezdőszám n, akkor az összeg 6.(2n+11). Így az összeg duplája se osztható 8-cal. Másrészt minden csúcsban ugyanannyi a befutó összeg, és ezen összeg 8-szorosa épp az élösszeg duplája. Ellentmondás.
|
| Előzmény: [1043] lorantfy, 2005-09-01 11:37:07 |
|
| [1043] lorantfy | 2005-09-01 11:37:07 |
 193. feladat: Ki lehet-e választani 12 db egymás után következő természetes számot úgy, hogy egy kocka éleire egyenként felírva őket, az egy csúcsban összefutó élekre írt számok összege egyenlő legyen?
|
|
|
| [1041] rizsesz | 2005-08-31 19:12:19 |
 Kedves lorantfy! Neked sincsen ötleted a Fibonaccis megfordítására? (ott van a tesztverseny topicban).
rizsesz
|
|
|
| [1039] lorantfy | 2005-08-31 17:32:22 |
 Szia Csimby!
Nagyon profi a megoldás! Gratula! Nem gondoltam, hogy ilyen gyorsan beírja valaki.
(Aki nem ismeri a kongruenciát először lássa be azt, hogy azonos kitevőjű hatványok maradéka egyenlő, ha az alapok maradéka megegyezik!)
|
| Előzmény: [1036] Csimby, 2005-08-31 17:16:51 |
|
|
| [1037] rizsesz | 2005-08-31 17:19:04 |
 2222 = 3 (mod 7), míg 5555=4 (mod 7). 3 hatványai a következő maradékokat adják 7-tel osztva: 3, 2, 6, 4, 5, 1... és innentől kezdve ismétlődés van. 4 hatványai: 4, 2, 1, 4, 2... 5555 = 5 (mod 6) és 2222 = 2 (mod 3), így az összeg maradéka 5 + 2 = 0 (mod 7). (Biztos van elegánsabb is :))
|
|
|
| [1035] lorantfy | 2005-08-31 14:00:36 |
 192. feladat: Bbh. 22225555+55552222 osztható 7-tel!
|
|
| [1034] Yegreg | 2005-08-21 22:33:28 |
 Igen, tulajdonképpen ez a kombinatorikus. Csak lehet n2 golyó n dobozban, és az érdekel, hogy melyik golyók vannak együtt, vagy, ami az én első megoldásom volt az n2 gyerek n házban, és az érdekli őket, hogy kivel vannak egy házban. És akkor még lehet a kebvésbé szépen, de egyszerűen elintézős megoldás: az n2 faktoriális tényezői közt van k(amivel éppen egyszerűsíteni akarunk) egyszerese, kétszerese...és k-szorosával kétszer egyszerűsíthetünk, és ezzel n+1 k-t ejthetünk ki, amennyi kell, hiszen a nevezőben is n+1-iken van k. De ez hasonló a binomiális együtthatóshoz alapjában véve. Üdv:
Yegreg
|
|
| [1033] jonas | 2005-08-20 21:40:11 |
 Ezt ismerem, nagyon szép feladat.
A kombinatorikus megoldás ez lehet. Vegyünk n2 elemet n sorban és n oszlopban. Ezeknek (n2)! permutációja van. Csakhogy vehetjük azokat a permutációkat, amiket úgy kapunk, hogy minden soron belül permutálgatjuk az elemeket, és aztán a sorokat egymással permutáljuk. Két ilyen permutáció kompozíciója is ilyen. Az ilyen permutációk tehát az eredeti (n2)! rendű szimmetrikus csoportnak egy (n!)n+1 elemű részcsoportját alkotják.
|
| Előzmény: [1032] Yegreg, 2005-08-18 13:54:46 |
|
| [1032] Yegreg | 2005-08-18 13:54:46 |
 Helyes a megoldás, bár nem a legszebb megoldások közé tartozik, ezt nehogy sértésnek, vagy ilyesminek vedd, mert kiváló megoldás, csak a kombinatorikai azért elegánsabb, szerintem. Van még egy logikára épülő számvizsgáló megoldás, bár az hasonlít a tiedre, azt leszámítva, hogy az leginkább egy logikai következtetés, és nem kell binomiális együtthatókat írkálni, illetve van egy kombinatorikai megoldás, az talán a legelegánsabb. De más megoládok is lehetnek még. Üdv:
Yegreg
|
| Előzmény: [1030] nadorp, 2005-08-18 09:44:25 |
|
| [1031] Lóczi Lajos | 2005-08-18 12:54:33 |
 Vettem az első két egyenlet rezultánsát x szerint, majd az eredmény és a harmadik egyenlet rezultánsát y szerint. (Közös gyöke két (többváltozós) polinomegyenletnek csak ott lehet, ahol a rezultáns nulla.)
|
| Előzmény: [1029] xviktor, 2005-08-17 22:30:28 |
|
| [1030] nadorp | 2005-08-18 09:44:25 |
 Ez egy számolós megoldás. Szerintem van tisztán kombinatorikai is, vagy valami polinomiális tételes is, ezt egyelőre nem találtam. Jelöljük a kifejezést A-val. Ekkor
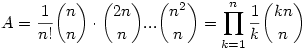 Itt minden tényező egész, ui. Itt minden tényező egész, ui.
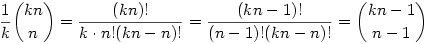
|
| Előzmény: [1025] Yegreg, 2005-08-16 22:48:40 |
|
|
|
| [1027] Lóczi Lajos | 2005-08-17 21:33:21 |
 Kiküszöbölve az egyenletekből pl. x-et és y-t, z-re az alábbi egyenletet kapjuk:
4z8+230z6+81297z4+41720z2+71824=0.
Erről az egyenletről viszont világosan látszik, hogy nincs valós megoldása, csak komplex, tehát az eredeti egyenletrendszernek sincs valós megoldása.
|
| Előzmény: [1026] xviktor, 2005-08-17 18:38:28 |
|
| [1026] xviktor | 2005-08-17 18:38:28 |
 191. Feladat: Oldjuk meg a kovetkezo egyenletrendszert a valos szamok halmazan:
1.:x2+y2-xy=225
2.:x2+z2-xz=121
3.:y2+z2-yz=36
Jo gondolkodast: Viktor
U.i.: Hogy lehet megcsinalni, hogy a 3. egyenlet a tobbi alatt legyen?
|
|
| [1025] Yegreg | 2005-08-16 22:48:40 |
 Én nem feltétlenül tekinteném különböző megoldásnak, annyi, hogy én felbontottam a szab. háromszöget 3 egyenlószárú háromszögre. Itt egy feladat, ezt nem én találtam ki, csak hallottam, és tetszett, talán azért, mert egész gyorsan megoldottam:)
Bizonyítsuk be, hogy az 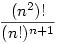 kifejezés bármely n (nyilván természetes szám) esetén egész! Több megoldást is lehet adni rá! kifejezés bármely n (nyilván természetes szám) esetén egész! Több megoldást is lehet adni rá!
Üdv:
Yegreg
|
|
| [1024] Lóczi Lajos | 2005-08-16 19:10:57 |
 Szép megoldás!
(Egy TeX-es megjegyzés a környező feladatokhoz: amikor koszinuszt/szinuszt írtok be, használjátok a "backslash"-t előtte, így olyan formátumot kapunk, ahogyan a könyvekben szokás: cos x-et, és nem cosx-et, ami utóbbi a c, o és s változók szorzata szokott lenni. Hasonló igaz a többi beépített függvénynévre is, pl. log x és nem logx.)
|
| Előzmény: [1021] xviktor, 2005-08-16 17:17:14 |
|
| [1023] xviktor | 2005-08-16 18:22:24 |
 Jo a megoldasod mutatok egy masikat is...
A forgasszimmetria miatt:
1.: A belso haromszog egy szabalyos haromszog, melynek terulete: 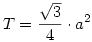
2.: A 3 kis haromszog egybevago. Felirtam a cosinus tetelt egy kis haromszogre: a2=22+42-2.2.4.cos =20-16cos =20-16cos
1-2bol: 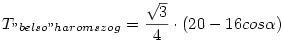
A kis haromszogek terulete /mindharome osszesen/: 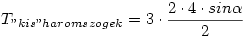
Igy a hatszog terulete: 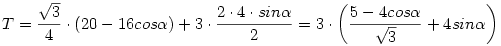
|
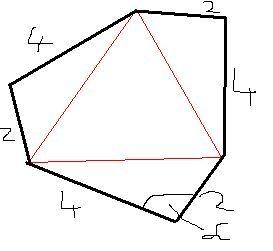 |
| Előzmény: [1022] Yegreg, 2005-08-16 17:36:10 |
|
| [1022] Yegreg | 2005-08-16 17:36:10 |
 A hatszöges feladatra írt képlet így jött ki: Vagyünk 3 szomszédos csúcsot, és a két szélsőt kössük össze a 120°-os forgásszimmetria középpontjával. Ekkor a forgásszimmetria miatt(bármelyik 3 egymás melletti csúcsot választjuk) a hatszög területének 3-ada lesz a kapott négyszög területe. Ez eddig a külső 3-as szorzó, a zárójelben a négyszög területe van. A négyszög oldalai: 2, 4, a, a. Az első kettő a hatszög két oldala a másik kettő a szimmetria miatt egyenlő. Kössük össze egymással a két szélső pontot, ekkor a négyszög egy átlóját kapjuk, ami két háromszögre bontja a négyszöget, a külső egyértelműen meghatározott adott  belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor belső szögnél, hiszen két oldal és a közbezárt szög ismert, és ebből a belső háromszög is meg lett határozva, hiszen az egyik oldala a külsővel közös, a rajta fekvő szögek pedig nyilván 30°-osak. A külső háromszög területe ekkor
t1=4sin
. A behúzott átló legyen b! Ekkor b2=22+42-16cos a koszinusz tétel alapján. Ha behúzzuk a belső háromszög magasságát, akkor két egybevágó félszabályos háromszöget kapunk, ahol a nagyobb befogó a koszinusz tétel alapján. Ha behúzzuk a belső háromszög magasságát, akkor két egybevágó félszabályos háromszöget kapunk, ahol a nagyobb befogó 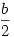 , a kisebb pedig így , a kisebb pedig így  , ami a belső háromszög magassága. A belső háromszög területe tehát , ami a belső háromszög magassága. A belső háromszög területe tehát

(valóban egyszerűsíthetünk). A hatszög területe pedig:
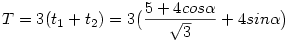
Ennyi. Üdv:
Yegreg
|
|
| [1021] xviktor | 2005-08-16 17:17:14 |
 A 189. feladat megoldasa szerintem:
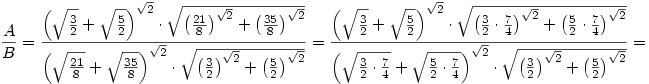
![=\frac{{\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac74\right)^{\sqrt2}\cdot \left[\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}\right]}}}{{\left[\sqrt{\frac74}\cdot\left(\sqrt{\frac32}+\sqrt{\frac52}\right)\right]^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}}=\frac{{\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}\cdot\sqrt{\left(\frac74\right)^{\sqrt2}}}{{\left(\sqrt{\frac74}\right)^{\sqrt2}\cdot\left(\sqrt{\frac32}+\sqrt{\frac52}\right)^{\sqrt2}\cdot \sqrt{\left(\frac32\right)^{\sqrt2}+\left(\frac52\right)^{\sqrt2}}}}=1](keplet.cgi?k=DF34C505BB17548F)
Eszreveheto, hogy az egyszerusitesek utan 1et kapunk. Igy A=B.
Amennyiben valamit elirtam legyszives szoljatok, es kijavitom.
Remelem jo a megoldasom: Viktor
|
| Előzmény: [1020] Lóczi Lajos, 2005-08-16 15:00:38 |
|
| [1020] Lóczi Lajos | 2005-08-16 15:00:38 |
 A különböző gyökkitevők egy összegben felcserélhetők?
189. feladat. Jelölje
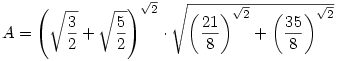
és
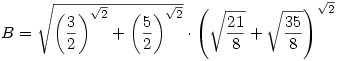
Döntsük el (majd bizonyítsuk be), hogy kettejük közül melyik a nagyobb szám.
|
|
| [1019] Lóczi Lajos | 2005-08-16 14:48:19 |
 Aki szeret térfogatot számolni, annak álljon itt a
188. feladat. Legyen a>0 adott szám és tekintsük a közönséges térbeli x-y-z koordinátarendszert.
Mekkora a térfogata annak a testnek, amely az x2+y2+z2 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2 4a2 egyenlőtlenséggel meghatározott gömb és az (x-a)2+y2 a2 (végtelen) henger metszeteként áll elő? a2 (végtelen) henger metszeteként áll elő?
|
|
|
|
| [1016] xviktor | 2005-08-15 23:28:27 |
 Annyibban igazad van, hogy tobb eset van, tehat egy altalanos kepletet keresunk, de szerintem nem jo a kepleted... bar lehet en tevedek
Es akkor a 187. feladat: a hatszog kore kor irhato. Mekkora a terulete?
Udv: Viktor
|
| Előzmény: [1015] xviktor, 2005-08-15 23:14:22 |
|
|
| [1014] Yegreg | 2005-08-15 21:01:22 |
 Bocsánat, úgy tűnik, hogy most sem vagyok képes normálisan beírni... egy zárójel elcsúszott. Helyesen így:
. Hiába, még nem vagyok rutinos TeX-es...:oD. Üdv:
Yegreg
|
|
| [1013] Yegreg | 2005-08-15 20:58:07 |
 Üdv!
Bocs, hogy csak most írok, de most értem haza, így nem tudtam reagálni a közbenső dolgokra. A beírt gömb sugara jogos, az egyenletet nem ismertem, kitalálni meg akkor este esélyem sem volt, pláne, hogy nem is gondolkoztam ilyesmiben(a bizonyítás amúgy nagyon szép szerintem). A sok számolás azért nem annyira sok, csak egy finom túlzás volt annak eltitkolása érdekében, hogy képtelen lettem volna beírni akkor este:). Valójában azt hiszem, hogy az pár Pitagorasz-tétel volt.
Az a hatszöges feladat nem akar összejönni Viktornak:) Vagy direkt csináltad először nem létezőre másodjára pedig több esetesre? Szóval a 186(azt hiszem) feladat megoldása:
Ahol alfa valamelyik belső szög. A 120°-os forgásszimmetria nem határozza meg egyértelműen a hatszöget, csak 3-3 belső szöge egyenlő egymással, két különböző belső szög összege pedig 240°. Egyébként szerintem a feladat normálisan körbe írt hatszög lenne. Akkor egyértelműen  =120°, és akkor kiszámolható a terület(akkor máshogy is számolható). Üdv: =120°, és akkor kiszámolható a terület(akkor máshogy is számolható). Üdv:
Yegreg
|
|
| [1012] xviktor | 2005-08-14 17:59:30 |
 Gratulalok, mindenki megoldasa helyes. De a 186. feladatra meg nem jott megoldas...
Jo gondolkozast: Viktor
|
|
| [1011] lorantfy | 2005-08-14 16:26:14 |
 185-höz: Kössük össze a poliéder csúcsait a beírt gömb középpontjával. Így a poliéder térfogatát sokszög alapú gúlák térfogatának összegére bontottuk, melyek magassága éppen a beírt kör sugara, alapjaik területének összege pedig a poliéder felszine.
Igy aztán: 
|
| Előzmény: [1010] xviktor, 2005-08-13 01:19:00 |
|
| [1010] xviktor | 2005-08-13 01:19:00 |
 Gratulalok szepek a megoldasaid /181,182,183/, a 184-et meg atgondolom en kicsit maskepp csinaltam,de szerintem az is jo.
A 183. feladatnal irtad hogy sok szamolas volt, pedig nagyon egyszeruen meg lehet allapitani a beirt gomb sugarat:
Tetel: Barmely poliederbe beirt gomb sugara: 
185. feladat: Bizonyitsuk be a fenti tetelt.
186. feladat: A 181. feladatot kisse fogalmazzuk at. Ha ahelyett hogy kor irhato bele azt mondanam, hogy 120°os forgasszimmetrikus, akkor mekkora lenne a terulete? /Ilyen hatszog letezik ;-)/
Jo gondolkodast: Viktor
|
| Előzmény: [1009] Yegreg, 2005-08-13 00:49:02 |
|
| [1009] Yegreg | 2005-08-13 00:49:02 |
 181.:
Ilyen hatszög nem nagyon van, hiszen ha egy 2 egység hosszú oldalt a kör x-re és 2-x-re bont, akkor az az x melletti 4 egység hosszú oldalt x-re és 4-x-re bontja, hiszen a körhöz külső pontból húzott érintő szakaszok egyenlőek, illetve továbblépve a 4-x melletti 2 egység hosszú oldalra, azt a körnek 4-x és 2-(4-x)-re kell bontania, szintén az érintő szakaszok miatt, azonban 2-(4-x)=x-2, csak akkor pozitív, ha x nagyobb, mint kettő, x azonban nem lehet nagyobb kettőnél, mert akkora szakaszt metszett le a kör egy másik két egység hosszú oldalból, tehát ha a beírt kör nem mehet át csúcson(azaz azt a sokszög teljes egészében tartalmazza), akkor nincs ilyen hatszög.
182:
20 3-as maradéka 1, 21-é 2, és belátható, hogy innentől kezdve periodikus, hiszen a 2 kétszerese mindig 4, aminek a 3-as maradéka mindig egy, az 1 kétszerese pedig mindig 2, aminek a 3-as maradéka kettő, ezzel a ciklus végére értünk. Látható tehát, hogy minden páratlan kitevő esetén 2 a hármas maradék. A 2333+2555-1 esetében a két kettő hatvány kitevője páratlan, hármas maradékuk 2 és 2, ezek összege 4, mínusz egy az 3, tehát az összeg osztható 3-mal, és mivel nagyobb nyilván, mint három, így nem lehet prím.
183:
Sok számolgatással(amit most nem szeretnék leírni, mert úgyis félreírnám) megkapjuk, hogy szabályos tetraédernél:
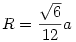
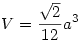

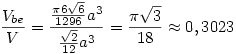
184:
Ha összekötjük a négy alsó gömb középpontját a vele szomszédosokkal, valamint az alsó 4-ét a felsőjével, akkor egy négyzet alapú gúlát kapunk, aminek minden oldala R.(ezt be lehet látni, hiszen érintik egymást) Ennek a gúlának a magassága 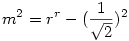 (Pitagoras tétel alapján) (Pitagoras tétel alapján)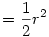 Ebből Ebből  Amiből ha meg akarjuk kapni a földtől való tárvolságot, akkor még hozzá kell adni Amiből ha meg akarjuk kapni a földtől való tárvolságot, akkor még hozzá kell adni 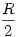 , hiszen a gúla ilyen magasan van, ekkor tehát az 5. gömb távolsága a talajtól: , hiszen a gúla ilyen magasan van, ekkor tehát az 5. gömb távolsága a talajtól:

És azt hiszem, ennyi feladat volt. Bocsánat, hogy 1, nincs ábra 2, nincs túl sok számolás leírva 3, ha valahol számolási hibát vétettem , de késő van már.
Üdv:
Yegreg
|
|
| [1008] xviktor | 2005-08-12 16:41:51 |
 Mostanaban hallottam par jo kis feladatot, gondoltam beirok ide parat.
181. feladat: Van egy hatszog mely oldalai: 2,4,2,4,2,4 /ebben a sorrendben/. Mekkora a hatszog terulete, ha tudjuk, hogy kor irhato bele?
182. feladat: Kicsit maskepp irom be ide mint az eredeti feladatban szerepel, hogy szamologepet ne lehessen hasznalni: Bizonyitsuk be hogy 2333+2555-1 nem prim!
183. feladat: Van egy szabalyos tetraederunk. A tetraederbe irt gomb terfogata hany szazaleka a tetraeder terfogatanak?
184. feladat: Van negy ugyanakkora sugaru gomb, melyek egy vizszintes asztalon paronkent erintik egymast. Pontosan kozepre "felrakunk" egy 5., a lentiekkel megegyezo sugaru gombot. Milyen messze van a fenti gomb kozeppontja a talajtol?
Jo gondolkodast!
|
|
|
|
|





 -x helyettesítést. Ekkor egy egyenletet kapunk az ismeretlen integrálra, ahol szerepelni fog egy másik integrál is, ami azonban elemien kiszámolható (egy arkusz tangenses összetettfüggvény-derivált). A végeredmény:
-x helyettesítést. Ekkor egy egyenletet kapunk az ismeretlen integrálra, ahol szerepelni fog egy másik integrál is, ami azonban elemien kiszámolható (egy arkusz tangenses összetettfüggvény-derivált). A végeredmény: 

 -ig 1 legyen.
-ig 1 legyen. (F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy
(F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy 


 <2 esetén létezik
<2 esetén létezik

 1 lehet.
1 lehet. 


 [0,1] rögzített és tekintsük az
[0,1] rögzített és tekintsük az  ex minden valós x-re, továbbá a mértani sor összegképletét.
ex minden valós x-re, továbbá a mértani sor összegképletét. 

 (2t-sin t,2t+cos t)
(2t-sin t,2t+cos t)
 , ami =R.(2x)/24. Persze R itt is az eredeti kúp sugara.
, ami =R.(2x)/24. Persze R itt is az eredeti kúp sugara.  5,33cm jon ki.
5,33cm jon ki. 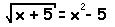
 k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2
k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2
 35555=(35)1111=2431111
35555=(35)1111=2431111