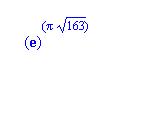| [2019] Tappancsa | 2007-04-27 19:08:15 |
 Remélem ez még nem volt.
318. feladat: Gondoltam egy polinomra (p(x)). Az együtthatói pozitív egész számok. Ki tudod-e találni a polinomomat, ha két x értékre hajlandó vagyok megmondani p(x) értékét?
Anikó
|
|
| [2018] HoA | 2007-04-26 16:59:36 |
 Persze. A feladat tehát az, tippeljük meg, legalább hányan állnak kettejük között, ha mobilon beszélnek. Elég 3? Vagy ahhoz hangosan szólni is elég, a mobilozáshoz inkább 6 kell? Stb.
|
| Előzmény: [2017] jonas, 2007-04-26 14:32:31 |
|
|
| [2016] HoA | 2007-04-25 16:43:11 |
 Talán azért érdemes itt foglalkozni ezzel a feladattal, mert szerintem ez a tipikus példája annak, milyen feladatot nem szabad iskolai versenyen feladni. Ugyanis a feladat szövege nem zárja ki azt, hogy Előd és Vali között nem áll senki. És innen nem matematikai, hanem nyelvészeti vagy filozófiai kérdés, van-e értelme 0 ember harmadáról beszélni, vagy a "még akkor is" jelentheti-e azt, hogy nem csökkent az előttem állók száma.
Tehát a megoldás: Ha Előd és Vali között nem áll senki, akkor Vali előtt ( a 0/3 távozása után is) Előd + az Előd előtt állók állnak. Ez csak úgy lehet kétszerese az Előd előtt állóknak, ha Előd előtt 1 ember áll. Ekkor Előd mögött 8-an, tehát Vali mögött 7-en állnak.
Ha előzetes megfontolások nélkül egyenleteket írunk fel, és az Előd előtt állók számát x-szel, az Előd és Vali között állókét y-nal, a Vali mögött állókét pedig z-vel jelöljük, a két megállapítás egyenlete:
y + z + 1 = 8x
2/3 y + 1 +x = 2x
Amiből z = 13/3 y + 7
Itt a feladat kitűzői nyilván elvárják a nyolcadikosoktól, hogy vegyék észre, mivel z egész, y csak 3-mal osztható egész lehet és mint "emberek száma" nem negatív. És itt ismét előjön a kérdés, megengedett-e y=0, ekkor persze z=7, vagy y legkisebb értéke 3 , amiből z=20 a helyes megoldás.
|
| Előzmény: [2013] Matthew, 2007-04-24 21:06:10 |
|
|
|
| [2013] Matthew | 2007-04-24 21:06:10 |
 Üdv mindenkinek!
Tudom,hogy ez a fórum középiskolásoknak van,de éppen ezért szeretnék tőletek segítséget kérni,mert én még csak 8.-os vagyok Tegnap volt a megyei Makkosházi Matematika Versenyen,amin én is elindultam,főleg tapasztalatszerzés céljából.Jókeddvel kezdtem neki a feladatoknak,mert 4 feladatra volt 70 percem,de aztán kiderült,hogy vagy én vagyok gyenge matekból,vagy a feladatok bonyolultabbak.Mindenesetre abban kérnék segítséget,hogy a feladatokat hogyan kellett volna megoldanom,és hogy mi a megoldásuk?.Ha jól tudom(de lehet,hogy rosszul emlékszem),akkor a Kömal is támogatta az iskolát a verseny megrendezésében,tehát lehet,hogy a feladatokat is ismerik éhányan,de azért leírom az elsőt,amire bevallom,közel 35 percem ment el:
Seft Előd és Kár Vali a hosszú sorban állás közben mobilon beszélgetnek.Előd végignézve a soron,megállapítja,hogy "Mögttem nyolcszor annyian vannak,mint előttem." Ezután Vali is "népszámlálást" végez és közli:"Remélem a köztünk lévők harmada itt hagyja és elmegy! De még akkor is kétszer annyian lesztek előttem,mint ahányan előtted vannak."
Legalább hányan lehettek Vali mögött?
Üdv.:Matthew
|
|
| [2012] jonas | 2007-04-24 13:22:18 |
 Hasonló feladat, hogy rakj le húsz érmét az asztalra úgy, hogy minden sorban és minden oszlopban öt legyen.
A megoldás, hogy egymásra kell rakni két érmét:
|
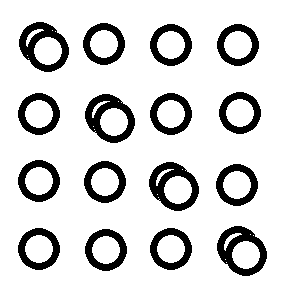 |
| Előzmény: [2008] DirtyD, 2007-04-24 11:48:07 |
|
| [2011] Sirpi | 2007-04-24 13:10:26 |
 Nem akartam bő lére ereszteni a magyarázkodást, képet meg pláne nem akartam hekkelni :-) Szóval köszi a kiegészítést, és tényleg így teljes értékű a megoldás.
|
| Előzmény: [2010] jonas, 2007-04-24 12:25:26 |
|
| [2010] jonas | 2007-04-24 12:25:26 |
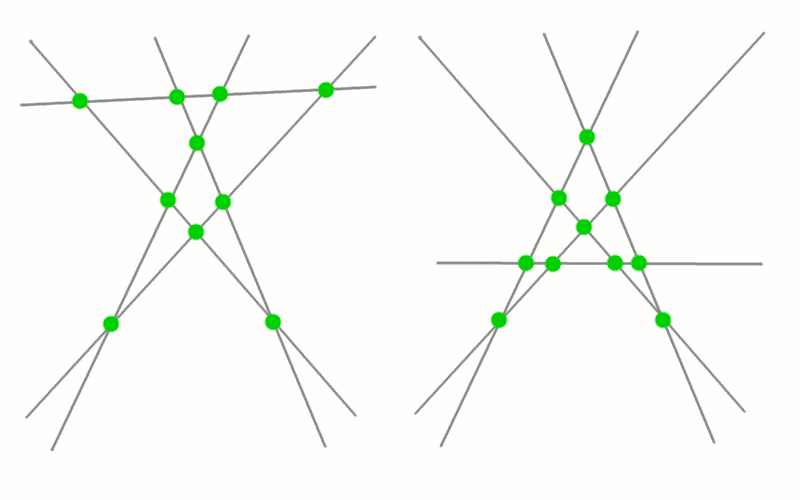
 Ha így tálalod a megoldást, akkor rejtvényújság-szaga van. Mondjuk inkább azt, hogy öt általános helyzetű egyenes metszéspontjai. Ez speciálisan a csillagötszöget is tartalmazza, de más helyzet is elképzelhető.
|
 |
| Előzmény: [2009] Sirpi, 2007-04-24 11:53:50 |
|
|
| [2008] DirtyD | 2007-04-24 11:48:07 |
 Sziasztok! Még új vagyok és remélem, hogy nem szerepelt még a következő feladat: Van 10 facsemete, amit 5 sorban úgy kellene elültetni, hogy minden sorba 4 csemete legyen! Lehet nagyon gagyi, de a baráti társaságban még senki nem oldotta meg!
|
|
|
|
|
|
|
|
|
|
| [1999] jonas | 2007-04-21 23:05:14 |
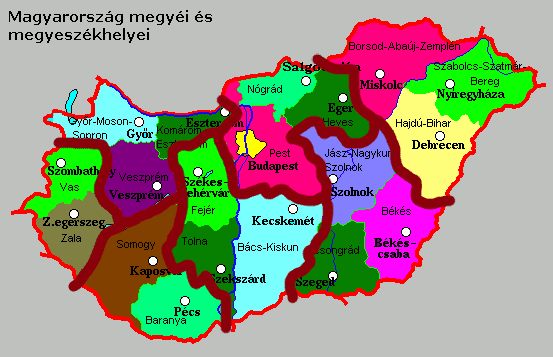
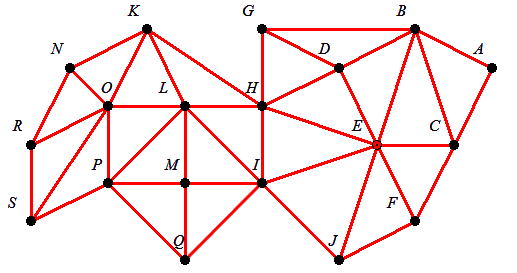
 Ha jól látom, nincs négy páronként szomszédos megye, tehát háromnál többet nem lehet összevonni. Ez azt jelenti, hogy legalább |-19/3-|=7 megye biztosan marad.
Ennyit viszont pont létre lehet hozni.
|
 |
| Előzmény: [1998] lorantfy, 2007-04-21 22:16:26 |
|
| [1998] lorantfy | 2007-04-21 22:16:26 |
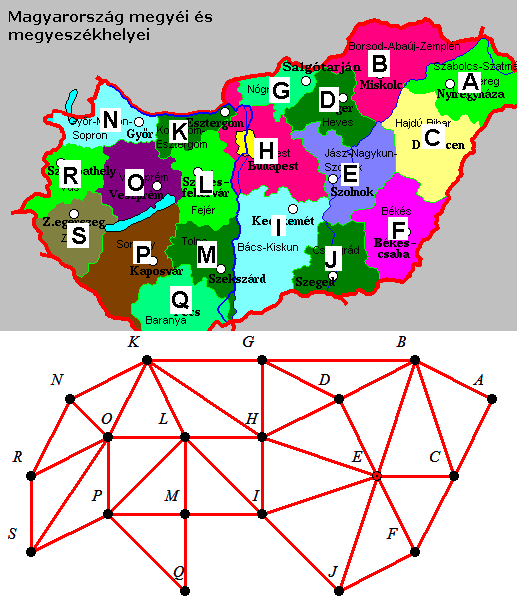
 306. feladat: Legalább hány megye lesz Magyarországon, ha
1. Bármely két megyét összevonhatunk, ha szomszédosak.
2. Nem kerülhet egy új megyébe két régi megye, ha eredetileg nem voltak szomszédosak.
|
 |
|
| [1997] Csimby | 2007-04-19 21:02:54 |
 Ja, megértettem, csak az nem volt világos múltkor, hogy pl. 0,2,4,6,... sorozatból ha beteszed a 2-est az egyik, 4-est a másik halmazba, akkor attól még mi garantálja, hogy 6,8,10,... számtani sorozat nem kerül be teljes egészében az egyik halmazba. Köszi.
|
| Előzmény: [1993] jonas, 2007-04-18 20:54:31 |
|
|
| [1995] Lóczi Lajos | 2007-04-19 18:16:46 |
 Csakhogy a kérdésem arra vonatkozott, hogy xx (általában) végtelen sok értéke MIND legyen valós. Ezt a kritériumot az Általad megadott számok már nem mind teljesítik, legyen pl.  =1, ekkor xx végtelen sok értéke =1, ekkor xx végtelen sok értéke
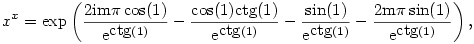
ahol m tetszőleges egész. Ha itt most m=1, akkor nemvalós szám adódik.
|
| Előzmény: [1994] Ali, 2007-04-19 10:50:57 |
|
|
| [1993] jonas | 2007-04-18 20:54:31 |
 Akkor megpróbálom mégegyszer elmondani, de még mindig szemléletesen, pontos indukciós feltétel nélkül.
Nyilván csak azokkal a számtani sorozatokkal kell foglalkozni, amiknek a kezdőeleme, és a differenciája is természetes szám (és az utóbbi nem nulla). Ilyen számtani sorozatból csak megszámlálható sok van, valahogy tehát sorba rendezzük őket úgy, hogy mindegyiket hozzárendeljük  egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n  -ra. -ra.
Utána a két halmazt lépésenként konstruáljuk meg úgy, hogy kiindulunk az A0={} és B0={} üres halmazokból, és bővítjük őket, amíg végül teljesítik a feltételeket. Azt szeretnénk elérni, hogy egyik halmaznak se legyen teljes egészében része valamelyik a fenti számtani sorozatokból, amit úgy érhetünk el, hogy minden számtani sorozatból berakunk egy elemet az A halmazba, és egyet a B halmazba. Ez elég, mert a két halmaz végig diszjunkt lesz.
Így aztán a következőképpen járunk el. Ha már megvan az An és Bn halmaz, akkor ezekből az An+1 és Bn+1 halmazokat egy-egy természetes szám hozzáadásával kapjuk meg, a két számot pedig úgy választjuk ki, hogy (1) mindkettő benne legyen az Sn számtani sorozatban, (2) különbözzenek egyástól és az An Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An Bn véges, így még mindig végtelen sok szám marad nekünk, amelyek közül kettőt ki kell választani. Bn véges, így még mindig végtelen sok szám marad nekünk, amelyek közül kettőt ki kell választani.
Például tegyük fel, hogy A1={0},B1={1},A2={0,2},B2={1,3}. Utána S2={0+2k}={0,2,4,6,8,....} amiből ki kell válsztanunk két olyan elemet, ami az A2 B2-ben nincs benne, ezek lehetnek a 4 és a 6, így aztán A3={0,2,4},B3={1,3,6} stb. B2-ben nincs benne, ezek lehetnek a 4 és a 6, így aztán A3={0,2,4},B3={1,3,6} stb.
Miután így minden n  -ra megkaptuk az An és Bn halmazokat, legyen A*= -ra megkaptuk az An és Bn halmazokat, legyen A*= nAn és B*= nAn és B*= nBn. Ez a két halmaz diszjunkt, és mindkettő tartalmaz legalább egy elemet minden érdekes számtani sorozatból. Az viszont még nem feltétlenül teljesül, hogy együtt minden természetes számot tartalmaznának (noha úgy is könnyen végre lehetne hajtani az indukciós lépést, hogy ez is teljesüljön), ezért legyen A= nBn. Ez a két halmaz diszjunkt, és mindkettő tartalmaz legalább egy elemet minden érdekes számtani sorozatból. Az viszont még nem feltétlenül teljesül, hogy együtt minden természetes számot tartalmaznának (noha úgy is könnyen végre lehetne hajtani az indukciós lépést, hogy ez is teljesüljön), ezért legyen A= -B* és B=B*. Mivel A* -B* és B=B*. Mivel A* A és B* A és B* B, ezért továbbra is mindkét halmazban van minden sorozatból elem, viszont az is igaz, hogy A B, ezért továbbra is mindkét halmazban van minden sorozatból elem, viszont az is igaz, hogy A B= B= és A és A B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket. B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket.
|
| Előzmény: [1989] Csimby, 2007-04-18 17:08:10 |
|
| [1992] SAMBUCA | 2007-04-18 20:45:34 |
 Na most hátha:)
(1)(4,5,6)(11,12,13,14,15)(22,23,24,25,26,27,28)...
(2,3)(7,8,9,10)(16,17,18,19,20,21)(29,30,31,32,33,34,35,36)...
azaz 1 ide, 2 oda, 3 ide, ...
|
| Előzmény: [1985] Csimby, 2007-04-18 02:23:52 |
|
|
|
| [1989] Csimby | 2007-04-18 17:08:10 |
 Biztosan bennem van a hiba, de nem teljesen értem a megoldásodat. Mindenesetre meg lehet adni két konkrét halmazt melyekről rögtön látszik hogy jók. És Sirpinek igaza van :-)
|
| Előzmény: [1987] jonas, 2007-04-18 08:09:56 |
|
| [1988] Yegreg | 2007-04-18 16:53:38 |
 érdekes, Sirpi konstrukciója sokkal természetesebb, mint az enyém, nekem eszembe sem jutott, de akkor már leírom az enyémet is: a számok kanonikus alakjában a prímkitevők összege szerint csoportosítunk. Így elég [log2(n)]+1 csoport, és nyilván nem lesz egy csoportban osztó és többszörös.
|
|
| [1987] jonas | 2007-04-18 08:09:56 |
 315. Persze, hogy fel lehet. Csak egy kis indukció kell hozzá.
Felsorolod az összes (nem konstans) végtelen számtani sorozatot, ami természetes számokból áll. Ilyenből persze csak megszámlálható sok van. Sorba mész rajtuk, és mindegyikből egy elemet beraksz az első halmazba, aztán egyet a második halmazba. Mivel úgy csináltad a felsorolást, hogy mindegyik számtani sorozat előtt csak véges sok másik van, csak véges sok számról döntöttél véglegesen, tehát van még két olyan szám, amivel el tudod rontani a soron jövő sorozatot. Végül a maradék természetes számokat berakod az első halmazba.
|
| Előzmény: [1985] Csimby, 2007-04-18 02:23:52 |
|
|
| [1985] Csimby | 2007-04-18 02:23:52 |
 [100 ]+1. feladat Fel lehet-e bontani a természetes számok halmazát két részhalmazra úgy, hogy egyikben se legyen végtelen számtani sorozat? ]+1. feladat Fel lehet-e bontani a természetes számok halmazát két részhalmazra úgy, hogy egyikben se legyen végtelen számtani sorozat?
|
|
| [1984] Sirpi | 2007-04-17 23:55:41 |
 Konstrukió (lehet máshogy amúgy?):
{1},{2,3},{4,5,6,7},{8,9,10,11,12,13,14,15}...
|
| Előzmény: [1983] Yegreg, 2007-04-17 17:05:52 |
|
| [1983] Yegreg | 2007-04-17 17:05:52 |
 semmi baj, tényleg gyorsan meg lehet oldani, viszont valóban a konstrukció az érdekesebb része, kíváncsi vagyok, hogy ti is azt a konstrukciót adjátok-e, mint én találtam
|
|
| [1982] Sirpi | 2007-04-17 16:04:29 |
 Hát így kapásból log2k elég, és annyi kell is, mert a 2-hatványokat mind külön kupacba kell rakni. Bocs a gyors lelövésért (nem is írom le a teljes konstrukciót), nem ismertem, csak gyorsan végiggondoltam :-) Jó feladat amúgy.
|
| Előzmény: [1981] Yegreg, 2007-04-17 14:38:30 |
|
| [1981] Yegreg | 2007-04-17 14:38:30 |
 Egy egyszerű, de szerintem érdekes feladat (ami úgy "jutott eszembe", hogy egy másik feladatot rosszul olvastam el :) )
Adottak az 1, 2, ... k számok. Legalább hány csoportba kell osztani őket, hogy ne legyen egy csoportban sem osztó-többszörös?
|
|
| [1980] Lóczi Lajos | 2007-04-17 10:02:58 |
 i-gen, hiszen 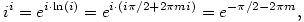 ahol m tetszőleges egész. ahol m tetszőleges egész.
Persze i ellentettje éppúgy jó. (Ezután azt a kérdést tettem fel magamnak, van-e még ezeken kívül ilyen tulajdonságú komplex szám. Azt találtam, hogy végtelen sok van, de csak megszámlálható, a valós részüket egy egyszerű képlet megadja, a képzetes részüket meg egy kicsit bonyolultabb. Akinek van kedve, keresse meg ezeket a "rácspontokat" a síkon.)
|
| Előzmény: [1979] ágica, 2007-04-17 07:53:44 |
|
|
|
| [1977] Lóczi Lajos | 2007-04-15 20:10:22 |
 Szerintem nem, pl. a k=0 esetben rögtön valós lesz z, amit kizártunk. De mondjuk a k=1, a= esetén kapott z:= esetén kapott z:= +i +i tg (1) sem lesz jó, hiszen tetszőleges m egész szám esetén fennáll, hogy tg (1) sem lesz jó, hiszen tetszőleges m egész szám esetén fennáll, hogy
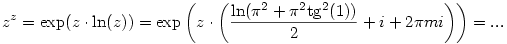
Itt véve pl. az m=0 esetet a következő számot kapjuk:
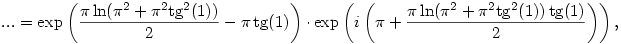
ami sajnos nem valós.
|
| Előzmény: [1976] Cckek, 2007-04-15 12:03:09 |
|
|
| [1975] Lóczi Lajos | 2007-04-12 22:53:58 |
 [100 ]. feladat. Adjunk példát olyan x komplex, de nem valós számra, hogy xx minden értéke valós. ]. feladat. Adjunk példát olyan x komplex, de nem valós számra, hogy xx minden értéke valós.
|
|
|
|
|
|
|
| [1969] Alma | 2007-04-12 18:14:51 |
 Nekem is valami hasonló jött ki, csak én megkaptam a végtelen sok megoldást. Nem kell sokat változtatni az előző megoldáson, csak egy icipicit: a) 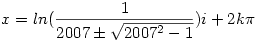 A b) eseten még nem gondolkoztam. A b) eseten még nem gondolkoztam.
|
| Előzmény: [1968] Lóczi Lajos, 2007-04-12 13:53:55 |
|
|
|
|
| [1965] Lóczi Lajos | 2007-04-11 22:22:31 |
 313. feladat. Adjuk meg az összes olyan x (komplex) számot, amelyre
a.) cos (x)=2007
b.) 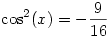 . .
|
|
|
| [1963] Cckek | 2007-04-09 10:40:38 |
 Kellemes ünnepeket mindenkinek.
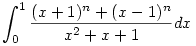 mely n-re racionális? mely n-re racionális?
|
|
| [1962] Cckek | 2007-04-06 07:35:31 |
 Ha már algebrai strukturáknál tartunk... Legyen A egy 4 elemű gyűrű. A akkor és csak akkor test ha az x2+x+1=0 egyenletnek van egy gyöke A-ban.
|
|
|
| [1960] Lóczi Lajos | 2007-04-02 01:28:13 |
 (Még néhány ilyen típusú, érdekes feladatot illetően l. pl. Szendrei-Czédli-Szendrei: Absztrakt algebrai feladatok, JATEPress, 1993. Az itteni feladat amúgy a Gyűrűk fejezet 15. feladatában szerepel.)
|
| Előzmény: [1959] nadorp, 2007-04-01 18:31:09 |
|
| [1959] nadorp | 2007-04-01 18:31:09 |
 Először oldjunk meg egy egyszerűbbet, nevezetesen: Ha egy gyűrűben 1-ab invertálható, akkor 1-ba is az. Megoldás:
Feltehető, hogy sem "a" sem "b" nem a zéróelem. Legyen (1-ab)c=1, azaz abc=c-1. Ekkor
babc=bc-b
babca=bca-ba
ba=bca-babca=(1-ba)bca
1-ba=1-(1-ba)bca. Tehát
(1-ba)(1+bca)=1, azaz 1-ba jobb inverze 1+bca. Hasonlóan adódik a bal inverzre is ugyanez az érték.
Mivel (xy)2=x(yxy) és (yx)2=(yxy)x ezért ha 1-(xy)2 inverze c, akor az előzőek szerint 1-(yx)2 inverze 1+yxycx
|
| Előzmény: [1956] Cckek, 2007-03-31 20:27:37 |
|
|
|
| [1956] Cckek | 2007-03-31 20:27:37 |
 Bizonyítsuk be, hogy ha egy gyűrűben az 1-(xy)2 elem invertálható, akkor 1-(yx)2 is invertálható.
|
|
|
|
| [1955] Cckek | 2007-03-29 20:11:02 |
 Hány számjegye van 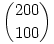 -nak? -nak?
|
|
|
|
|
| [1949] Cckek | 2007-03-27 10:19:18 |
 Bizonyítsuk be, hogy az (R,+) és (C,+) csoportok izomorfak.
|
|
| [1948] Lóczi Lajos | 2007-03-24 21:55:34 |
 Deriváljuk az integrált az x paraméter szerint, majd használjuk a jól ismert 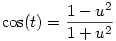 helyettesítést, ahol u=tan (t/2). Ekkor az u változó szerint egy racionális törtfüggvényt kapunk, aminek van elemi primitív függvénye. Visszahelyettesítve a t változót az alábbit kapjuk: helyettesítést, ahol u=tan (t/2). Ekkor az u változó szerint egy racionális törtfüggvényt kapunk, aminek van elemi primitív függvénye. Visszahelyettesítve a t változót az alábbit kapjuk:
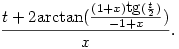
Ennek a megváltozása kell t=0 és t= között. A függvény t=0-ban 0, a t között. A függvény t=0-ban 0, a t  - határesetben pedig x-től függően kétféle értéket vesz fel: vagy nullát vagy 2 - határesetben pedig x-től függően kétféle értéket vesz fel: vagy nullát vagy 2 /x-et. Már csak x szerint kell a primitív függvényt visszakeresni, ami persze triviális. (Az x=0, x=1, x=-1 eseteket persze külön meg kell vizsgálni az eredeti határozott integrálban.) /x-et. Már csak x szerint kell a primitív függvényt visszakeresni, ami persze triviális. (Az x=0, x=1, x=-1 eseteket persze külön meg kell vizsgálni az eredeti határozott integrálban.)
Végeredmény: az eredeti integrál értéke 0, ha -1 x x 1, míg 2 1, míg 2 log |x|, ha x>1 vagy x<-1. log |x|, ha x>1 vagy x<-1.
|
| Előzmény: [1947] Cckek, 2007-03-24 19:44:40 |
|
| [1947] Cckek | 2007-03-24 19:44:40 |
 312.feladat Ha már integráloknál tartunk:
Számítsuk ki a következő integrált:
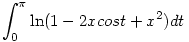
|
|
|
| [1945] Lóczi Lajos | 2007-03-20 03:00:23 |
 311. feladat. Mekkora a tangensfüggvény négyzetgyökének görbe alatti területe 0 és  /4 között? /4 között?
|
|
|
| [1943] Csimby | 2007-03-11 13:39:10 |
 309.feladat Van e olyan valós szám amelynek bármely egész számrendszerben felírt alakjában minden számjegy szerepel legalább egyszer.
310.feladat Igaz-e, hogy additív halmazfüggvények szorzata is additív?
Amúgy nincs kedvetek visszatérni a feladatok sorszámozásához? Szerintem az olyan jól bejött eddig...
|
|
|
| [1941] Lóczi Lajos | 2007-03-10 18:10:09 |
 Elképzelhető, hogy mi nem tudjuk megoldani a feladatot, mert nehéz; azért írtam be csak, mert meglepően egyszerű s szép a végeredménye. Inkább sejtsük meg numerikusan, vagy keressük meg az interneten az értékét, illetve, hogy ki az, aki rátalált erre a formulára. (Bár azt is el tudom képzelni, hogy igazából nem is számít, hogy pontosan prímekről van benne szó, és esetleg elég lenne egy alsó/felső becslés az n-edik prímszámra, és abból is ugyanaz az érték jönne ki?)
|
| Előzmény: [1940] Cckek, 2007-03-10 17:25:37 |
|
|
| [1939] Lóczi Lajos | 2007-03-09 23:53:09 |
 Jelölje pn az n-edik prímszámot.
Határozzuk meg a 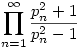 végtelen szorzat értékét. végtelen szorzat értékét.
|
|
|
|
|
|
|
| [1933] Doom | 2007-03-06 07:29:59 |
 Legutóbb rossz helyre tettem, remélem itt már jó...
Egy 'a' oldalú szabályos háromszög minden csúcsában 1-1 kutya áll (A, B és C), majd egyszerre elkezdenek futni egymás felé azonos sebességgel: A B felé, B C felé és C pedig A irányában. Mennyi idő múlva találkoznak?
Segítségként egy "sejtés": egy furcsa "spirál-alakot" megtéve a háromszög középpontjában fognak találkozni, mégpedig egyszerre.
|
|
| [1932] Cckek | 2007-03-01 23:37:51 |
 Így sem érthető teljesen, és nem is tudom, hogyan lehetne ezt helyesen megfogalmazni, de abban az esetben ha n=ab, amit egy egyenlőtlenség helytelen alkalmazásával kapunk!!
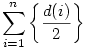 , jön ki, ahol {x} az x , jön ki, ahol {x} az x R törtrészét jelöli. Erre gondoltál?? R törtrészét jelöli. Erre gondoltál??
|
| Előzmény: [1930] S.Ákos, 2007-02-28 16:02:40 |
|
|
| [1930] S.Ákos | 2007-02-28 16:02:40 |
 Elnézést kérek az érthetelenségért és a lassú reagálásért
1) n Z+ Z+
2) az ai-k [a,b] intervallum beli valós számok, és föggetlenül választásuktól reciprokösszegük is [a,b]-beli valós szám lesz
3) ha n db valós számot választasz ki, lehetséges, hogy lesz több olyan [a,b] intervallum, amelyre teljesül 2),  (n) ezek számát jelöli egy adott n-hez (n) ezek számát jelöli egy adott n-hez
És a feladat helyesen: Határozzuk meg ![\sum_{i=1}^n\varepsilon(i)-\bigg[\frac{d(i)}2\bigg]](keplet.cgi?k=F5E4CF8B69D417E5) pontos értékét!-Remélem, így érthetőbb pontos értékét!-Remélem, így érthetőbb
|
| Előzmény: [1922] jenei.attila, 2007-02-26 20:16:10 |
|
|
|
|
|
| [1925] nadorp | 2007-02-26 21:39:15 |
 Szia Cckek !
Kicsit gyorsan reagáltál :-), de azért egy heurisztikát én is vázolnék ( nem bizonyítás, de szerintem befejezhető, a Te megoldásod viszont teljesen korrekt)
Legyen 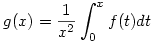 (x>0). Ekkor (x>0). Ekkor
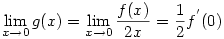 . Tehát . Tehát
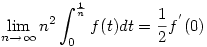 . A kérdéses szumma éppen a balodalnak egy integrálközelítő összege. . A kérdéses szumma éppen a balodalnak egy integrálközelítő összege.
|
| Előzmény: [1923] Cckek, 2007-02-26 20:25:22 |
|
|
|
| [1922] jenei.attila | 2007-02-26 20:16:10 |
 Ákos ne haragudj, de ez teljesen értelmetlen amit írsz. Próbáld meg légyszíves világosabban megfogalmazni. Pl. Mi az n, mi köze a reciprok összegnek az az ai-khez rendelt valós számokhoz (talán az ai-k maguk [a,b] intervallumbeli valós számok? Egyáltalán mik az ai-k)és mit jelent a "jelölje az n-hez tartozó intervallumok számát  (n)" mondat? (n)" mondat?
|
| Előzmény: [1918] S.Ákos, 2007-02-25 19:24:35 |
|
|
|
|
|
|
|
| [1915] Cckek | 2007-02-24 10:29:37 |
 Az 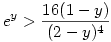 egyenlőtlenség igazolása: Legyen egyenlőtlenség igazolása: Legyen
f:(0,1) R, f(y)=y-ln (1-y)+4ln (2-y). R, f(y)=y-ln (1-y)+4ln (2-y).
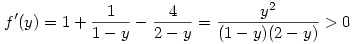 , tehát a függvény szigoruan nő, így , tehát a függvény szigoruan nő, így
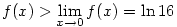 , tehát , tehát
y-ln (1-y)+4ln (2-y)>ln 16 az-az
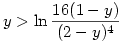 . .
|
| Előzmény: [1911] Cckek, 2007-02-22 21:43:46 |
|
|
| [1913] Lóczi Lajos | 2007-02-23 11:46:57 |
 Jól ismert a binomiális sorfejésbo"l, hogy vannak olyan c1,c2 pozitív állandók, hogy minden, elég kis abszolút értéku" x esetén fennáll az

egyenlo"tlenség; egyébként pl. c1=c2=1 megfelelo" az |x| 1 halmazon. 1 halmazon.
Ebbo"l a közrefogási elvvel és az
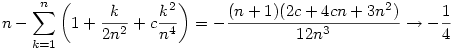
(n  ) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4. ) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4.
|
| Előzmény: [1908] Cckek, 2007-02-22 15:09:59 |
|
|
|
|
| [1909] Lóczi Lajos | 2007-02-22 19:41:12 |
 Valaki azt állította, hogy a
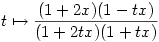
függvény (t-szerinti) határozott integrálja 0 és 1 között minden pozitív x esetén kisebb 1-nél. Igaza van-e neki?
|
|
|
|
|
| [1904] tim20 | 2007-02-22 07:16:52 |
 Egy furcsa fa első nap 1,1/2-szeresére nőtt. Másnap az előző nap 1,1/3-szorosára, harmadnap az előző nap 1,1/4-szeresére és így tovább. Hány nap alatt nőtt meg az eredeti magasságának 100-szorosára?
|
|
| [1903] Cckek | 2007-02-19 19:35:39 |
 Nagyon szép. Gratulálok.
|
|
| [1902] Lóczi Lajos | 2007-02-19 11:30:24 |
 A kerdeses yn sorozat konvergens:
lathato, hogy minden indexre 0<xn<1. Ezt es a rekurziv definiciot hasznalva adodik, hogy
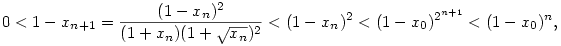
s igy n 1 eseten 1 eseten
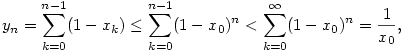
vagyis yn monoton no es felulrol korlatos.
A feladat kituzesehez a motivaciot nyilvan a (gyokvonasra szolgalo) Newton-iteracio adta, hiszen a megadott rekurzio nagyon hasonlit hozza, es a konvergenciasebesseg is olyan ("a helyes tizedesjegyek szama minden lepesben megduplazodik").
|
| Előzmény: [1896] Cckek, 2007-02-16 08:26:44 |
|
|
|
|
| [1898] HoA | 2007-02-16 14:51:17 |
 Lehet, hogy elírtad, de mivel mindkét helyen négyszer szerepel a "tucat", a két kifejezés értéke 0,5.tucat4 illetve 6.tucat4 , tehát mindenképpen a második a nagyobb, függetlenül attól, hogy a tucat milyen pozitív számot jelöl.
|
| Előzmény: [1895] tim20, 2007-02-16 06:01:09 |
|
| [1897] Lóczi Lajos | 2007-02-16 11:30:43 |
 Nyilvan nagyon hasonlo a ket megoldas, de igy utolag megnezve, a megoldasomban valojaban nem is kell kihasznalni, hogy az eredeti an sorozat monoton novo, sem azt, hogy konvergens, csupan azt, hogy mindig (0,1)-ben van (es persze a lenyegi 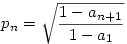 osszefuggest). osszefuggest).
|
| Előzmény: [1896] Cckek, 2007-02-16 08:26:44 |
|
| [1896] Cckek | 2007-02-16 08:26:44 |
 Sajnálom, elsiettem:)) De az csak jó lehet ha egy feladatra két szép megoldás is van a forumon. Amúgy azt hiszem az an 1,n 1,n  határértékből és határértékből és
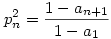
összefüggésből már következik, hogy pn nullsorozat.
Itt van még egy:
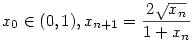 . .
Konvergens-e az yn=n-(x0+x1+...+xn-1) sorozat?
|
| Előzmény: [1894] Lóczi Lajos, 2007-02-15 11:40:09 |
|
| [1895] tim20 | 2007-02-16 06:01:09 |
 Melyik a több? Fél tucat tucat tucat tucat, vagy hat tucat tucat tucat tucat? A második vagy az első vagy egyenlőek?
|
|
| [1894] Lóczi Lajos | 2007-02-15 11:40:09 |
 Varhattal volna meg egy fel napot a leirassal :) de mivel tegnap 2 orat gondolkodtam a feladaton, beirom az en megoldasomat is.
Jeloljon n mindvegig nemnegativ egeszt. Konnyu latni, hogy an monoton no es minden n-re 0<an<1.
Legyen 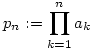 es szokas szerint p0:=1. A rekurziv osszefuggesbol kapjuk, hogy 1-an+1=(1-a1).pn2. es szokas szerint p0:=1. A rekurziv osszefuggesbol kapjuk, hogy 1-an+1=(1-a1).pn2.
Mivel 0<pn monoton fogyo, ezert konvergens. Indirekten tegyuk fel, hogy pn p>0. A monotonitas miatt ekkor persze minden n-re pn>p, azaz -pn2<-p2. p>0. A monotonitas miatt ekkor persze minden n-re pn>p, azaz -pn2<-p2.
Mivel tetszoleges valos x eseten x=1-(1-x) e-(1-x), ezert e-(1-x), ezert
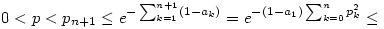
e(1-a1)(-1-p2.n).
Ha most n  , a jobb oldal tart 0-hoz. Az adodo ellentmondas mutatja, hogy pn valoban nullsorozat. , a jobb oldal tart 0-hoz. Az adodo ellentmondas mutatja, hogy pn valoban nullsorozat.
|
| Előzmény: [1893] Cckek, 2007-02-14 19:51:20 |
|
| [1893] Cckek | 2007-02-14 19:51:20 |
 Ez a feladat túl szép ahoz, hogy megoldatlanul maradjon:
a1 (0,1) Ha ak (0,1) Ha ak (0,1) akkor ak+1=ak2(ak-1)+1, de -1<ak-1<0 tehát 1-ak2<ak2(ak-1)+1<1 az-az ak+1 (0,1) akkor ak+1=ak2(ak-1)+1, de -1<ak-1<0 tehát 1-ak2<ak2(ak-1)+1<1 az-az ak+1 (0,1). A matematikai indukció elve szerint an (0,1). A matematikai indukció elve szerint an (0,1), (0,1), n n N. N.
an+1-an=an3-an2-an+1=(an-1)2(an+1)>0 tehát an növekvő. Legyen an határértéke l. Ekkor l=l3-l2+1,l [0,1] tehát l=1. Tehát létezik egy bn csökkenő sorozat, bn [0,1] tehát l=1. Tehát létezik egy bn csökkenő sorozat, bn 0 úgy hogy an=1-bn. Írhatjuk: 0 úgy hogy an=1-bn. Írhatjuk:
1-bn+1=(1-bn)3-(1-bn)2+1 bn+1=bn(1-bn)2 ezért bn+1=bn(1-bn)2 ezért
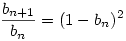
ahonnan tagonként felírva majd összeszorozva kapjuk, hogy
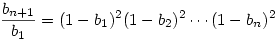 ahonnan ahonnan 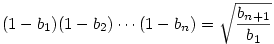 . .
Tehát
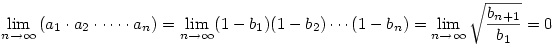
|
| Előzmény: [1890] Cckek, 2007-02-10 12:44:33 |
|
| [1892] jonas | 2007-02-12 18:03:59 |
 A feladatot nem találtam meg, de az állítást a Járai-könyvben igen (162. oldal).
Ez azt állítja, hogy a racionális számok halmaza nem áll elő megszámlálhatóan sok nyílt halmaz metszeteként.
|
| Előzmény: [1854] jonas, 2007-01-31 15:08:11 |
|
| [1891] HoA | 2007-02-10 16:32:44 |
 Mint matektanárunk szokta mondani, az eredmény közlése nem egyenlő a feladat megoldásával. Ha valakinek kell egy kis segítség az ilyen típusú feladatok megoldásához, hát lássuk: 1. megközelítés. Ki mond igazat?
I: Az első ajtó mond igazat -> a nyeremény a 2. mögött van -> a 2. is igazat mond -> ellentmondás azzal, hogy csak egy mond igazat
II: a második ajtó mond igazat -> mivel csak egy ajtó mond igazat, az 1. ajtó hazudik -> a 3. is igazat mond -> ellentmondás azzal, hogy csak egy mond igazat
III. a harmadik ajtó mond igazat -> mivel csak egy ajtó mond igazat, az 2. ajtó hazudik -> a nyeremény a 3. mögött van -> az 1. hazudik -> JÓ MEGOLDÁS
2. megközelítés: Hol a nyeremény?
I: Az első ajtó mögött -> 1. hazudik, 2. igazat mond, 3. igazat mond -> két igazmodó: ellentmondás
II: A második ajtó mögött -> 1. igazat mond, 2. igazat mond -> két igazmodó: ellentmondás
III: A harmadik ajtó mögött -> 1. hazudik, 2. hazudik, 3. igazat mond -> JÓ MEGOLDÁS
|
| Előzmény: [1889] Anum, 2007-02-10 11:00:54 |
|
| [1890] Cckek | 2007-02-10 12:44:33 |
 Az 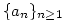 sorozat a következőképpen adott: sorozat a következőképpen adott:
a1 (0,1), an+1=an3-an2+1. (0,1), an+1=an3-an2+1.
Számítsuk ki a következő határértéket:
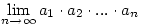 . .
|
|
|
| [1888] tim20 | 2007-02-10 10:28:37 |
 Sziasztok!
3 ajtó közül az egyik mögött nyeremény rejtőzik. Ám az ajtók közül csak az egyik mond igazat. Melyik ajtó mögött találod a nyerményed? 1.ajtó: "A 2-es mögött van." 2.ajtó: "Nem a 3-as mögött van." 3.ajtó: "Az 1-es hazudik!"
Lehetőségek:
1. ajtó 2. ajtó 3. ajtó nem lehet meghatározni, hogy melyik mögött van egyik mögött sincs
|
|
| [1887] Cckek | 2007-02-06 17:33:44 |
 Valóban szép interpolációs polinom, akkor az ajánlom szerkesszük meg trigonometrikus interpolaciós polinomját is, úgy hogy 1,2,3,...,8 helyeken a polinom ezeket az értékeket vegye fel:)
|
| Előzmény: [1886] HoA, 2007-02-06 16:48:13 |
|
| [1886] HoA | 2007-02-06 16:48:13 |
 Igazán díjazom a humorotokat, de azért ne hülyítsük az ifjúságot! LócziLajos rámutatott, hogy tetszőleges y1,y2,...,yk racionális értékekhez megadható olyan, legfeljebb k-1 -edfokú racionális együtthatós polinom, mely az 1,2, ... , k helyeken éppen az adott értékeket veszi fel ( vagy máshol, ld. második példa ) Ekkor persze mondhatjuk, hogy megvan a "szabály" , a sorozat folytatása a polinom következő egész helyeken felvett értéke.
Bohner Géza ötlete még keményebb, tkp. azt mondja, bármi megfelel, aminek az eleje megegyezik a megadottakkal. Mondjuk az adott számok Hófehérke és a hét törpe születésnapjának "nap" részei, és a következő szám a királyfi szülinapjának "nap"-ja. (Hogy ezeket honnan tudjuk, az más kérdés :-))
Félretéve a tréfát, nem mindig olyan egyértelmű rájönni az "igazi" szabályra, vagyis arra, amire a feladat kitűzője gondolt. Nekem már jött ki IQ-teszt -szerű feladatokban más "következő száma a sorozatnak" mint ami a megoldások között szerepelt, pedig igyekeztem a feladatkitűzők matematikai szintjére "emelkedni".
|
| Előzmény: [1884] BohnerGéza, 2007-02-06 12:42:04 |
|
|
| [1884] BohnerGéza | 2007-02-06 12:42:04 |
 Még az előző hozzászólásénál is egyszerűbb szabály!
Legyen a sorozat első nyolc tagja 1,4,9,7,7,9,13,10, majd a többi tetszőleges, például 77, 77, 77, ...
Azért a feladat feladója valószínűleg Cckek [1881]-ben adott válaszára gondolt!
|
| Előzmény: [1878] tim20, 2007-02-06 10:15:01 |
|
| [1883] Lóczi Lajos | 2007-02-06 12:12:31 |
 Inkább nekem higgyél! "Négyzetszámok", meg "számjegyek összege" ... brrr, de bonyolult. Vegyük csak az egyszerű racionális számokat és a polinomokat, hiszen már az ókoriak is...
1. Nézzük a
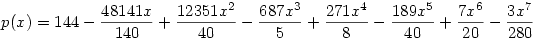
polinomot. Itt p(1)=1,p(2)=4,p(3)=9,...,p(8)=10. A 9. tag tehát -99 lesz, mert p(9)=-99.
Csak ez a megoldás lehet jó! Kipróbáltam ugyanis: vettem egy másik polinomot, mondjuk:
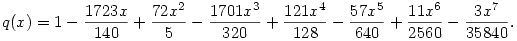
Nocsak! Páros helyeken tökéletes az egyezés: q(0)=1,q(2)=4,q(4)=9,...,q(14)=10. Mivel 14+2=16 és q(16)=-99, a sorozat 9. helyén álló szám tényleg a -99.
:-)
|
| Előzmény: [1878] tim20, 2007-02-06 10:15:01 |
|
|
|
|
| [1879] Sirpi | 2007-02-06 10:46:11 |
 ...9, 1, 4, 9, 16, 16, 9, 13, 19, 9, 10, 4, 9...
Egyelőre nem lőném le, annyi segítség, hogy az elejéből látszik, hogy a négyzetszámokhoz van köze a dolognak.
|
| Előzmény: [1878] tim20, 2007-02-06 10:15:01 |
|
| [1878] tim20 | 2007-02-06 10:15:01 |
 Sziasztok!
Találtam egy feladványt, de nem jövök rá a logikájára, pedig biztosan egyszerű. Szerintetek mi lesz a következő szám ebben a számsorban: 1,4,9,7,7,9,13,10, ?
Ugye valaki tud segíteni?
|
|
|
| [1876] Lóczi Lajos | 2007-02-06 02:52:19 |
 Ez a feladat nem más, mint apró általánosítása annak a jól ismert elemi állításnak, hogy egy konvergens sorozat limesze azonos a sorozatból képezett számtaniközép-sorozat limeszével.
Jelölje xn limeszét X, Y jelentése hasonló. Jelölje K a két sorozat abszolútértékének egy közös felső korlátját.
Nyilván azt kell igazolni, hogy
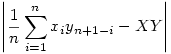
nullsorozat. De ezt -- az AB-CD=A(B-D)+D(A-C) összefüggés figyelembe vételével -- nyilván felülről becsülhetjük az alábbival:
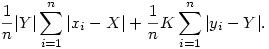
A befejezéshez elég megmutatni, hogy ezek nullsorozatok. Nyilván elég azt belátni, hogy ha xn X, akkor X, akkor 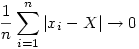 . .
Rögzítsünk egy  >0 számot, és legyen N( >0 számot, és legyen N( ) az a küszöbindex, melyre minden n>N( ) az a küszöbindex, melyre minden n>N( ) esetén |xn-X|< ) esetén |xn-X|< . Legyen n>N( . Legyen n>N( ). Ekkor ). Ekkor
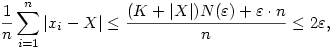
ha n elég nagy.
|
| Előzmény: [1874] Cckek, 2007-02-05 17:27:15 |
|
| [1875] pogre | 2007-02-05 17:41:49 |
 nah én tök béna vok a matekhoz tehát ne nevessetek ki a feladatommal!!! A sugarak intenzitása exponenciálisan csökken anyagokba való behatoláskor! 6mm mélységben az intenzitás az eredeti 10 százalékára csökken csökken!
a) Írj fel formulát az intenzitás csökkenésére b)mekkora lesz az intenzitás 2mm mélységben
|
|
|
|
| [1872] Cckek | 2007-02-05 16:59:26 |
 Találkoztam egy nagyon érdekes feladattal, persze nem tudom megoldani:(
Legyenek xn, yn konvergens sorozatok. Bizonyítsuk be, hogy
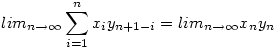
|
|
| [1871] Mhari | 2007-02-05 15:44:28 |
 Sziasztok!
Köszönöm Nektek - Lóczi Lajos és Cckek - a gyors megoldást,tetszik mindkettőtöké, de a lelkivilágomhoz mégis Cckek-é áll közelebb, az olyan "hagyományos", rendezgetős, számolgatós. Én próbálkoztam mindennel, ami a fejemből kifért, de erre az egyszerű dologra nem is mertem gondolni, hogy a 4xy így bontsam fel. Hát hiába, aki tud, az tud. Üdv: Attila
|
|
| [1870] Cckek | 2007-02-05 05:10:02 |
 A legegyszerűbb talán ha a baloldali kifejezést tényezőkre bontjuk:
3x2+4xy+y2=3x2+3xy+xy+y2=3x(x+y)+y(x+y)=(3x+y)(x+y).
Mivel p prímszám ezért csak a következőképpen írható fel egész számok szorzataként:
1.p, p.1, (-1).(-p), (-p).(-1).
Tehát négy egyenletrendszert kell megoldanunk:
3x+y=1,x+y=p vagy 3x+y=p,x+y=1, 3x+y=-1,x+y=-p vagy 3x+y=-p,x+y=-1, ahonnan kapjuk a megoldáspárokat:
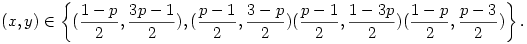
|
| Előzmény: [1867] Mhari, 2007-02-04 20:28:38 |
|
| [1869] Lóczi Lajos | 2007-02-04 21:17:47 |
 A megoldás:
Fejezzük ki a 3x2+4xy+y2=p egyenletből y-t a másodfokú egyenlet megoldóképletével. A gyökjel alatt x2+p áll, melynek nyilván teljes négyzetnek kell lennie, tehát valamely t egész számmal x2+p=t2. Itt p-re rendezve és faktorizálva kapjuk, hogy
1. t-x=1 és t+x=p
vagy
2. t-x=-1 és t+x=-p
3. t-x=p és t+x=1
4. t-x=-p és t+x=-1, amivel megoldottuk a kérdést.
|
| Előzmény: [1868] Lóczi Lajos, 2007-02-04 20:58:25 |
|
|
| [1867] Mhari | 2007-02-04 20:28:38 |
 Sziasztok! ...hát gyerekek, én csak ámulok és bámulok a sok rajzszög láttán, de nekem sokkal prózaibb gondom van már megint. Ahogy elnézlek benneteket, az én problémám nem is probléma (csak nekem). Szóval a probléma: 3*x*x+4*x*y+y*y=p Ahol x,y egészek, p pedig prím szám. Mi a megoldás?
Van ennek egy édestestvére, x*y*y+2*x*y+x-243*y=0 ahol x,y pozitív természetes szám, de azt simán meg lehet oldani, nehézség nélkül.(Még nekem is sikerült!)
De az elsővel sehogyan sem boldogulok. Próbáltam megoldani, mint felületet, még ábrázoltam is a Derive-val, jól is nézett ki, de nem sokra mentem vele. (Megjegyzem tudom a megoldást, 4 pár van belőle, de megoldani nem tudom.) Ha valaki tud, segítsen megoldani!
Üdv: Attila
|
|
| [1866] jonas | 2007-02-02 15:02:52 |
 Pontosan.
Továbbá az olcsóbb rajzszögeknél a tűt a fej lemezéből vágják ki és hajlítják ki, tehát ilyenkor a körlapból hiányzik egy szakasz, ami ugyanonnan indul, mint ahonnan a tű. Ilyen rajzszögekből is elfér kontinuum sok.
|
| Előzmény: [1865] Sirpi, 2007-02-02 13:36:53 |
|
| [1865] Sirpi | 2007-02-02 13:36:53 |
 Ha a tű nem indulhat kerületi pontból, akkor ez nem jelent általánosítást, hiszen minden rajzszög feje nyeshető úgy, hogy a tű a középpontból induljon.
Ha meg indulhat kerületi pontból (de továbbra sem lehet a fej síkjában), akkor simán el lehet kontinuum sokat helyezni.
|
| Előzmény: [1864] Csimby, 2007-02-02 10:38:55 |
|
| [1864] Csimby | 2007-02-02 10:38:55 |
 A hétvégén áttanulmányozom amiket írtál, csak most vizsgáztam és nem volt rá időm. Amúgy még egy általánosítási lehetőség, ha a tű nem a fej középpontjából indul.
|
| Előzmény: [1863] jonas, 2007-02-01 21:22:08 |
|
|
| [1862] jonas | 2007-02-01 21:16:38 |
 Ha ez működik így, akkor a gombás vagy T betűs ennek speciális esete. Sőt, a szállodásnak is, hiszen minden ember lenyelhet egy rajzszöget. Csak a nyolcasos feladatra nem ad semmit.
|
| Előzmény: [1861] jonas, 2007-02-01 21:11:53 |
|
| [1861] jonas | 2007-02-01 21:11:53 |
 Még egy ábra a bizonyítás második feléhez: a kék vonal (valójában gúla) fölé nem nyúlhat másik rajzszög, ezért ahol a kék és a piros vonal metszi egymást, a fölé nem érhet az adott rajzszög alatti másik rajzszög közepe.
(Megjegyzem, nem feltétlenül van egy rajzszög alatti következő rajzszög, a rajzszögek fölfele torlódhatnak.)
|
 |
| Előzmény: [1860] jonas, 2007-02-01 21:02:26 |
|
| [1860] jonas | 2007-02-01 21:02:26 |
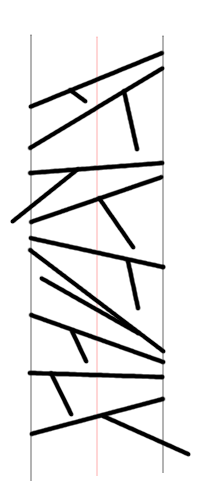
 Akkor most a változatosság kedvéért én próbálok meg egy bizonyítást a rajzszögesre (307. feladat).
Azt látom be, hogy megszámlálható soknál nem lehet több rajzszög. Tegyük fel ennek ellenkezőjét.
Először vegyünk egy olyan egyenes irányt, amivel megszámlálhatónál több rajzszög feje nem párhuzamos. Ilyen irány biztosan van: három páronként merőleges irány közül legalább az egyik biztosan ilyen.
Irányítsuk az összes fejet a szerint, hogy a kiválasztott irány mindegyiknek ugyanarra az oldalára mutasson. Két részre oszthatjuk a rajzszögeket a szerint, hogy a fejnek az előbbi irányítás szerint melyik oldalára áll ki a tűje. Vegyük a kettő közül csak a nagyobb csoportot.
Most vetítsük a rajzszögek fejét a kiválasztott irányban egy merőleges síkra -- kivéve azokat a rajzszögeket, amik párhuzamosak az iránnyal, tehát a vetületük lapos lenne. Vegyünk a síkon egy koordináta-rendszert, és vágjuk le az összes fejet olyan paralelogrammává, aminek ez a vetülete egy racionális koordinátájú téglalap, de azért a tű továbbra is a fej belsejéből induljon ki. Ilyen racionális koordinátájú vetületből csak megszámlálható sok van, tehát van megszámlálhatónál több olyan fej, aminek azonos a vetülete. (Lásd az ábrát.)
Vágjuk még le a rajzszögek tűit úgy, hogy ne lógjon ki a vetületük a fejek vetületéből.
Mármost nézzük a fejek közepét (ahol a piros egyenes metszi őket). Könnyen látható, hogy ha van egy rajzszögünk, akkor ehhez a tű irányában nem lehet akármilyen közel másik rajzszög, mert az nem metszheti sem a tűt, sem a fejet. Valójában ha a tű vége a vetítés irányában bizonyos távolságra van a fejtől, akkor a fej közepe a következő rajzszögek közepétől legalább fele ekkora távolságra van.
Ezért aztán mindegyik rajzszög közepétől a tűk irányában van egy pozitív hosszúságú szakasz, amin nincs másik rajzszög közepe. Ezen a szakaszon vehetünk egy racionális pontot, ezek mind különböznek, tehát csak megszámlálhatóan sok rajzszögünk lehet.
|
 |
| Előzmény: [1842] Csimby, 2007-01-31 12:23:56 |
|
|
| [1858] Lóczi Lajos | 2007-01-31 19:27:30 |
 Ha nem mértékelmélettel fogalakozó könyvet nézel, a Baire-tétel nem a végén lesz. A "Baire category theorem"-re rákeresve meg a neten a bizonyítást is könnyűszerrel felleled.
|
| Előzmény: [1854] jonas, 2007-01-31 15:08:11 |
|
| [1857] HoA | 2007-01-31 16:38:22 |
 Azt hiszem jó nyomon járok, ezek nálam is speciális esetek: Hogyan lehet egy biztos halálraitélt szavazatával éppen megúszni?
Ha a kalózhajót egy olyan rendszernek tekintjük, melynek állapotait a kalózok száma szerint A1,A2,..- vel jelöljük, akkor A2-től A204-ig bezárólag A203 az egyetlen instabil állapot: az ajánlattevőt vízbe dobják és A202 lép életbe. Jelöljük a kalózokat a sor végéről számolva K1,K2,...-vel. A204 azért is érdekes állapot, mert itt először nem egyértelmű, ki kap az aranyból. K204 számára az A202-es állapot 102 vesztese közül bármelyik 100 megfelel. Ezekkel, valamint a saját és a halálraítélt K203 szavazatával megvan az 50%-a. A kisebb indexű állapotokban mindig a megelőző állapot veszteseinek kellett adni, hiszen ha valaki csak ugyanannyit kap , mint a kalóz vízbedobása esetén biztosan, akkor a 3) szabály szerint ellenszavazóvá válik. Ha a szabályok pontosak, ez szerintem azt eredményezi, hogy a következő stabil állapotban (A208) - és a nagyobb indexűekben is - az osztó saját magán (K208) és a három "halálraítélten" (K205,K206,K207) kívül bármelyik 100-nak adhat 1-1 aranyat, hiszen A202 nyertesei ( = A204 biztos vesztesei ) valamint K203 és K204 biztosan jobban járnak vele, mint A204-ben; ha pedig A202 egyik vesztese kap, nem lép be a 3) szabály, hiszen ő nem lehet biztos benne, hogy K204 adna-e neki, a biztos esemény áll szemben egy kb. 98%-os valószínűséggel.
Itt abba is hagyom. Nyilván a feladatot már kielemezték, csak azt jelezd, ha valahol tévedek.
|
| Előzmény: [1840] Lacczyka, 2007-01-30 21:50:22 |
|
|
| [1855] Sirpi | 2007-01-31 15:25:56 |
 Hú, efölött valahogy elsiklottam, szemléletesen bennem egy egyenes rajzszög képe volt, és így hirtelen nem is látom, hogyan javítható a megoldásom. Mert akármennyire el lehet görbíteni. Ráadásul ezek a rajzszögek nem javíthatók úgy, mint az egyenesek, hogy nyesek belőlük, és akkor már csak megszámlálhatóan sok lehet, mert a kör és a szakasz szöge kontinuum értéket felvehet.
|
| Előzmény: [1853] jonas, 2007-01-31 15:05:14 |
|
| [1854] jonas | 2007-01-31 15:08:11 |
 A tétel a Baire-féle kategóriatétel volt, a könyv a Járai: Mértékelmélet, az okos ember Garay tanár úr, a verseny pedig, azt hiszem, a BME matematikaverseny két évvel ezelőtt.
A feladat és az állítás már nagyobb gond. Megpróbálok utánanézni.
|
| Előzmény: [1850] Csimby, 2007-01-31 14:25:51 |
|
| [1853] jonas | 2007-01-31 15:05:14 |
 Ügyes megoldás. Nem is gondoltam rá, hogy a különböző méretűeket külön vagyük.
Persze úgy, ahogy leírod, csak akkor működik, ha a rajzszögek tűje merőlegesen áll a fejére. Nézd:
|
 |
| Előzmény: [1851] Sirpi, 2007-01-31 14:41:18 |
|
|
| [1851] Sirpi | 2007-01-31 14:41:18 |
 Akkor a rajzszögesre belátom, hogy csak megszámlálható sokat lehet. Tegyük fel, hogy van egy olyan kitöltés, ahol a rajzszögek száma több, mint megszámlálható. Ekkor minden rajzszöget "nyessünk" meg. Vegyük a szár hosszát (l), és a kör sugarát (r), és mindkettőt csökkentsük le 1/n-re, ahol n egész. Ekkor továbbra is jó kitöltést kapunk.
Ezek után elég belátni, hogy minden n-re, ezekből az r=1/n, l=1/n méretű rajzszögekből csak megszámlálható sok fér el, ekkor az összes n-re együttesen is.
Ezt elég n=1-re belátni, a többi n-re csak hasonlóságot kell alkalmaznunk. Vegyük minden rajzszögön a szárnak a körhöz csatlakozó végpontjához közelebbi mondjuk 10-edelőpontját, és rajzoljunk köré 1/10 sugarú gömböt. Nem megyek bele a technikai részletekbe, de "szemléletesen látszik", hogy ezek a gömbök diszjunktak, aki akarja, beláthatja egzaktul. Mindben van rac. pont, így készen vagyunk.
|
| Előzmény: [1842] Csimby, 2007-01-31 12:23:56 |
|
|
| [1849] jonas | 2007-01-31 14:23:22 |
 Hát, a könnyűeket még a gimnáziumban tanultam Tünde nénitől.
A nehéz akkor merült fel, amikor egy versenyen beadtam egy feladatra egy félig jó megoldást, aminek a végén kijött az, hogy az állítás teljesül ha ez és ez a számosságos állítás igaz. Ez a megoldás (mivel csak egyirányú implikáció jött ki) csak akkor ér pontot, ha az a számosságos dolog tényleg igaz, ezért utólag megkérdeztem okos embereket, hogy igaz-e.
|
| Előzmény: [1848] Csimby, 2007-01-31 14:20:44 |
|
|
| [1847] jonas | 2007-01-31 14:15:33 |
 Ilyen számosságos feladatokból találkoztam már olyannal is, aminek a megoldását nem is értettem meg, mert valami tételt használt, ami csak a tankönyvek leghátában van benne, és ott is bizonyítás nélkül.
|
|
|
| [1845] jonas | 2007-01-31 13:39:06 |
 Aki akar gondolkozni a szállodás feladaton, az ne olvassa el ezt.
Az emberesre valami olyasmi volt a megoldás, hogy veszünk miden ember belsejében egy racionális koordinátájú pontot, és mivel ilyenből csak megszámlálható sok van.
Ilyen pont létezését persze csak akkor könnyű garantálni, ha az emberek tisztességes alakúak, mondjuk Borel-halmazok.
|
| Előzmény: [1844] Csimby, 2007-01-31 13:33:49 |
|
|
|
| [1842] Csimby | 2007-01-31 12:23:56 |
 307. feladat Hány rajzszög (körlap és középpontjából egy szakasz) fér el a térben?
308.feladat Amennyiben egy szállodához kontinuum sok hús vér három dimenziós ember érkezik, hogy szállásoljuk el őket, hány dimenziós ez a tér?
|
|
|
|
|
|
|
| [1836] Cckek | 2007-01-30 17:45:53 |
 Nos alkalmazva Sophie Germaine hires képletét kapjuk:
14+4.(2n)4=(22n+1-2n+1+1)(22n+1-2n+1+1) tehát a kifejezés akkor lehet prim ha az egyik tényező öt.
Így n=0 vagy n=1. De az n=0 esetben a kifejezés értéke 1.
|
| Előzmény: [1826] Lóczi Lajos, 2007-01-27 17:28:21 |
|
| [1835] HoA | 2007-01-30 13:09:49 |
 Köszönöm, megoldottam. tényleg nagyon jó. Már ha jónak lehet nevezni azt, ha látjuk, hogyan tudja egy valaki sok pénz elvételével az összes többit , minimális pénzük megtartásának reményében, egymás ellen kijátszani. :-)
|
| Előzmény: [1822] Lacczyka, 2007-01-26 21:24:37 |
|
|
|
|
|
|
|
| [1828] thukaert | 2007-01-27 18:43:24 |
 Ennek a számnak az első 12 tizedesjegye 9 -es, annak a valsége hogy valaki egy ilyet találjon tízezredrésze annak hogy ötöse legyen a lottón.Ramanujannak sikerült.Vajon hogy csinálta?
|
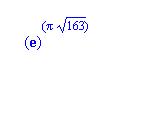 |
|
| [1827] thukaert | 2007-01-27 18:32:06 |
 A gyomos területek összkerületét vizsgáld, rá fogsz jönni, hogy ez változatlan marad , vagy csökken minden esetben amikor egy parcella elgyomosodik.
Kezdetbe az összkerület maximuma 4(n-1) Az elérni kívánt állapotban: 4n
Ez adja a feladat megoldását.
n gyomos parcella képes elgyomosítani az egészet, gondoljunk csak arra hogy keresztben vannak elhelyezve a gyomos parcellák.
Azt is elmondhatjuk, hogy n*n-n gyomos parcella esetén nem biztos hogy elgyomosodik az egész. n*n-n+1 esetén biztos .Ennek átgondolása némi időt igényel
|
| Előzmény: [1824] lorantfy, 2007-01-27 10:57:59 |
|
| [1826] Lóczi Lajos | 2007-01-27 17:28:21 |
 306. feladat. Adjuk meg azokat az n pozitív egészeket, amelyre 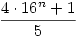 prímszám. prímszám.
|
|
|
| [1824] lorantfy | 2007-01-27 10:57:59 |
 Jó lenne újra számozni a feladatokat! Talán a 304. volt az utolsó számozott. Egy érettségi feladatsorban találtam az alábbi példát:
305. feladat: Egy négyzet alakú földterület n x n kisebb négyzetre van felosztva. Ha egy területrésznek legalább két szomszédja gazos, akkor ez a terület is elgazosodik.
Lássuk be, hogy n db gazos területrész elgazosíthatja az egész táblát, de n-1 db gazos területrész semmiképpen sem.
A feladat bármely általánosítása, továbbfejlesztése vagy hasonló feladat érdekelne. Ha valakinek eszébe jut ilyen, akkor legyenszíves nekem emilben elküldeni. Előre is köszönöm!
|
|
| [1822] Lacczyka | 2007-01-26 21:24:37 |
 Igazad van.. tényleg kimaradt... nem vagyok még gyakorlott TeX -használó, és az 50 százaléknál százalékjelet használtam, és így egy csomó minden kimaradt. Mindenesetre bocsánat a hibáért, itt a feladat:
Van 10 kalózunk, akik szereztek száz aranyat, és egy sajátos osztozkodási eljárással osztják szét. Sorba állítják magukat elvetemültség alapján, és a legelvetemültebb kalóz tesz egy osztozkodási ajánlatot: megmondja, hogy ki mennyit kap a 100 aranyból. Ezek után a kalózok szavaznak, és ha megvan az 50 százalék, akkor elfogadtatik a javaslat, ha nincs meg, akkor a kalózt vízbe dobják, és a második legelvetemültebb tehet ajánlatot, és így tovább. A szavazásnál annak a kalóznak a szavazata is számít, aki a javaslatot tette. A kalózok döntési elvei: 1)leginkább életben akarnak maradni. 2) pénzéhesek, vagyis úgy döntenek, ahogy több arany üti a markukat. 3) vérszomjasak: ha nem származik hátrányuk egy társuk halálából, akkor automatikusan nem szavazzák meg a javaslatát. Kérdés: hány aranyat tud megtartani magának a legelvetemültebb rabló? Egyáltalán, életben maradhat? A feladat megítélésem szerint nagyon jó... ha nem ismerted, akkor határozottan ajánlom figyelmedbe :)
|
| Előzmény: [1819] jonas, 2007-01-26 20:58:40 |
|
| [1821] tomii282 | 2007-01-26 21:09:40 |
 akk hogy is van ez a kalozos pelda?
|
|
| [1820] S.Ákos | 2007-01-26 21:05:42 |
 Legyen adott egy egységsugarú k1 kör a síkban. Hol van azon pontok mértani helye a síkban, amelyekből adott r sugárral rajzolt körnek és k1-nek a közös része éppen k1 területének a fele? 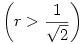
|
|
|
| [1818] tomii282 | 2007-01-26 20:38:19 |
 a kalozos feladatot h kell megoldani?
|
|













 =1, ekkor xx végtelen sok értéke
=1, ekkor xx végtelen sok értéke 
 k
k
 egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n
egyik eleméhez. Például legyen az első sorozat S0={0+1k}, a második S1={1+1k}, a harmadik S2={0+2k}, utána sorban S3={2+1k}, S4={1+2k}, S5={0+3k}, S6={3+1k}, S7={2+2k}, ... A sorrend nem is lényeges, csak az, hogy egy se maradjon ki, tehát minden ilyen számtani sorozat egyenlő Sn-nel valamely n
 Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An
Bn elemeitől is. Ilyen két számot mindig lehet választani, mert az Sn-nek végtelen sok eleme van, de An A és B*
A és B* B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket.
B=0. Ezért aztán az A és a B halmaz teljesíti a feltételeket. 



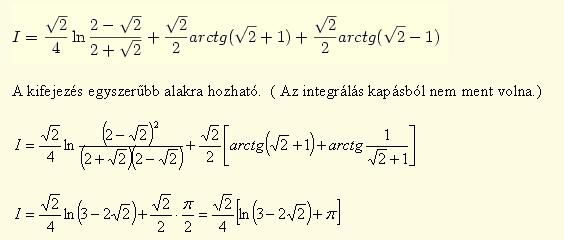

 x
x

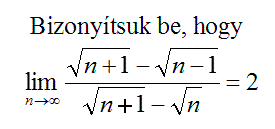
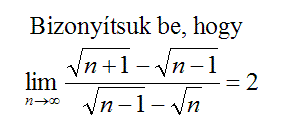

 (n) ezek számát jelöli egy adott n-hez
(n) ezek számát jelöli egy adott n-hez  ) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4.
) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4. 
 1 eseten
1 eseten  n
n bn+1=bn(1-bn)2 ezért
bn+1=bn(1-bn)2 ezért  1, akkor jobb oldal 1, a bal pedig
1, akkor jobb oldal 1, a bal pedig