|
|
|
|
|
| [2227] Gyöngyő | 2007-08-22 17:49:19 |
 Sziasztok!
Lenne egy olyan kérdésem,hogy hogyan lehet bebízonyítani,hogy 1>0 (egy nagyobb mint nulla)?
Köszönettel:
Gyöngyő
|
|
|
|
| [2224] Lóczi Lajos | 2007-08-22 12:07:23 |
 Gondolom, x valós. Ekkor elegendő a [0,2 ] intervallumot nézni. Mivel [ ] intervallumot nézni. Mivel [ ,2 ,2 ]-n a szinusz negatív és negatív alap esetén nehézkes a valós számok körében hatványokat értelmezni, ezért ezt a részt most hagyjuk ki. Marad a [0, ]-n a szinusz negatív és negatív alap esetén nehézkes a valós számok körében hatványokat értelmezni, ezért ezt a részt most hagyjuk ki. Marad a [0, ] intervallum. A koszinusz negatív ezen intervallum jobb felén. Marad [0, ] intervallum. A koszinusz negatív ezen intervallum jobb felén. Marad [0, /2]. Itt viszont az eredeti függvény tengelyesen szimmetrikus e legutóbbi intervallum felezőmerőlegesére, tehát elég [0, /2]. Itt viszont az eredeti függvény tengelyesen szimmetrikus e legutóbbi intervallum felezőmerőlegesére, tehát elég [0, /4]-re szorítkozni. /4]-re szorítkozni.
Az eredeti bal oldal x=0-ban éppen 1. De minden x (0, (0, /4)-re (sin x)cos x+(cos x)sin x>1, hiszen /4)-re (sin x)cos x+(cos x)sin x>1, hiszen
(sin x)cos x+(cos x)sin x (sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon. (sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon.
Azt is könnyű meggondolni, hogy (sin x)cos x+(cos x)sin x sosem lehet 2, hiszen 0 és 1 közötti számok 0 és 1 közé eső hatványa ugyanilyen, de egyszerre nem lehet mindkettő 1.
Ezekből az eredeti kérdésre a válasz már rögtön kiolvasható, ha nem tévedtem sehol.
|
| Előzmény: [2223] Cckek, 2007-08-22 10:13:55 |
|
| [2223] Cckek | 2007-08-22 10:13:55 |
 Oldjuk meg a (sin (x))cos (x)+(cos (x))sin (x)=k Z egyenletet:D Z egyenletet:D
|
|
|
| [2221] Cckek | 2007-08-10 17:43:13 |
 Köszi szépen Lajos a tanulmányokat, nagyon érdekesek, az említett azonosságra tudok egy indukciós bizonyítást, mely elég hosszú, ezért lettem volna kiváncsi más ötletekre...
|
| Előzmény: [2220] Lóczi Lajos, 2007-08-09 23:36:02 |
|
|
|
| [2218] Cckek | 2007-08-08 12:09:35 |
 Gyönyörűszép levezetés, gratula. Azt hiszem, hogy Cesaro-Stolzzal is megy, mármint ha nem csesztem el valahol:)
Első Stolz után 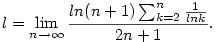
Második Stolz után: 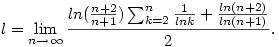
Már csak azt kell felhasználni, hogy 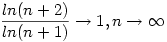 és és 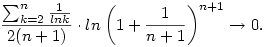
|
| Előzmény: [2217] nadorp, 2007-08-08 00:22:25 |
|
| [2217] nadorp | 2007-08-08 00:22:25 |
 Ennek nem lehet ellenállni :-) ( Remélem jó is lesz a megoldás)
Egy jelölés: Ha {an},{bn} két sorozat, akkor an bn jelölje az asszimptotikus egyenlőséget, tehát hogy bn jelölje az asszimptotikus egyenlőséget, tehát hogy 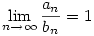 . Felhasználtam a következőket: . Felhasználtam a következőket:
a.) 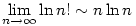
b.) Ha {an},{bn} két pozitív sorozat, és an bn valamint bn valamint 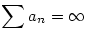 , akkor , akkor 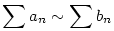
A feladatban szereplő összeg az alábbiak szerint is írható
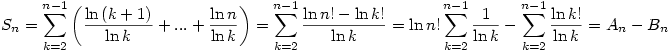
Belátjuk, hogy 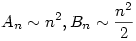 ,innen már következik ,innen már következik 
1.) 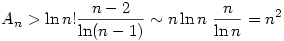
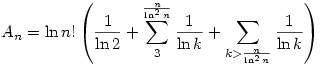
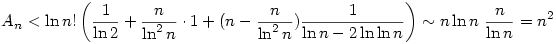
2.) Mivel 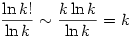 , ezért , ezért
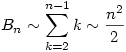
|
| Előzmény: [2213] Lóczi Lajos, 2007-08-07 00:22:27 |
|
|
|
| [2214] Cckek | 2007-08-07 12:23:30 |
 Tehát az eredmény valóban 6 :) Ha f:[a,b] [c,d] folytonos, növekvő, bijektív függvény akkor [c,d] folytonos, növekvő, bijektív függvény akkor 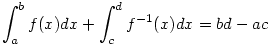 . .
A bizonyítás egyszerű, csak az f(x)=t jelölést kell használni.
Legyen
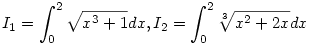 , ,
ekkor I=I1+I2. Jelölés 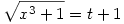 tehát tehát 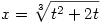 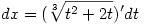 tehát tehát 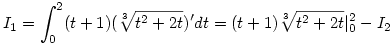
az-az I=6.
Természetesen észrevehető, hogy az előbb kijelentett tételt, egy kicsit más formában használtuk.
Ha f:[a,b] [a+ [a+ ,b+ ,b+ ] folytonos, növekvő, bijektív akkor ] folytonos, növekvő, bijektív akkor
![\int_{a}^{b}\left[f(x)+f^{-1}(x+\alpha )\right] dx=(b-a)(b+a+\alpha )](keplet.cgi?k=6DE24D46B6FB5774)
|
| Előzmény: [2212] Lóczi Lajos, 2007-08-06 20:56:35 |
|
|
| [2212] Lóczi Lajos | 2007-08-06 20:56:35 |
 Az eredmény (borzasztó nagy valószínűséggel) 6. A gép szimbolikus válasza csúnya hipergeometrikus függvényt és gammafüggvényt tartalmaz, de minden numerikus közelítés 6-ot ad.
Lássuk a levezetést és a tanulságokat! :)
|
| Előzmény: [2209] Cckek, 2007-08-04 20:12:02 |
|
| [2211] Csimby | 2007-08-04 23:55:24 |
 Mivel tudjuk, hogy zn is rajta van a komplex egységkörön (hiszen z rajta van), ezért zn szerintem már csak kétféle lehet, amiket írtam, z konjugált vagy -z hiszen ha z=a+bi akkor az y=-b egyenes legfeljebb két pontban metszi a komplex egységkört, -a-bi-ben és a-bi-ben.
|
| Előzmény: [2204] Cckek, 2007-08-04 17:00:39 |
|
|
|
|
| [2207] HoA | 2007-08-04 19:34:06 |
 Ugyanez egy kicsit másképp: n = 3k + 2 esetén zn+z+1=z3k+2+z+1=z2+z+1+z3k+2-z2=(z2+z+1)+z2(z3k-1) és itt a 3. primitív egységgyökök mindkét tagnak gyökei.
|
| Előzmény: [2200] Csimby, 2007-08-04 15:26:15 |
|
|
|
| [2204] Cckek | 2007-08-04 17:00:39 |
 Hogy a képzetes részek egymás ellentettjei ebből nem következik, hogy z és zn egymás konjugáltjai. Probáld inkább a z egységmoduluszú gyök akkor 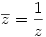 is gyök utat:) is gyök utat:)
|
| Előzmény: [2202] Csimby, 2007-08-04 16:43:26 |
|
|
| [2202] Csimby | 2007-08-04 16:43:26 |
 Másik biz., amiből kijön a másik irány is: t.f.h. van 1 absz. értékű z megoldás. Ekkor zn is 1 absz. értékű. Mivel z+zn=-1, ezért képzetes részeik egymás ellentettjei, vagyis z és zn egymás konjugáltjai vagy pedig z=-zn. A z=-zn eset kilőve, hiszen akkor z+zn nem -1 hanem 0. Marad az, hogy egymás konjugáltjai, ekkor viszont -1/2 a valós részük (hiszen összegük -1). És máris megkaptuk, hogy z csak 3. primitív egységgyök lehet. Ebből már következik, hogy n=3k+2 hiszen n=3k esetében zn=1, n=3k+1 esetében zn=z és csak n=3k+2 esetben lesz zn egyenlő z konjugáltjával.
|
| Előzmény: [2201] Cckek, 2007-08-04 15:29:15 |
|
|
| [2200] Csimby | 2007-08-04 15:26:15 |
 n=3k+2 esetén zn+z+1=(1+z+z2)(1-z2+z3-z5+...+zn-2) ahol a jobb oldal második tényezőjében váltakozó előjellel szerepelnek z növekvő hatványai és azok maradnak ki amelyekben a kitevő 3k+1 alakú. Mivel 1+z+z2-nek a 3. primitív egységgyökök gyökei és ezek 1 abszolútértékűek, ezért az egyik irány kész van.
|
| Előzmény: [2198] Csimby, 2007-08-04 15:09:43 |
|
|
|
| [2197] Cckek | 2007-08-04 12:53:25 |
 Egy olimpiászfeladat:
Bizonyítsuk be, hogy a zn+z+1=0 egyenletnek akkor és csakis akkor van egységnyi moduluszú komplex gyöke, ha n 3-mal való osztási maradéka 2.
|
|
| [2196] Hajba Károly | 2007-08-02 08:04:16 |
 OK. Akkor teljes szigorral csak n=7-re ismerünk megoldást.
Alacsony n-re szerintem nincs, ha van, akkor az magasabb n-re lesz. Ez minimum n>7, mivel n=7-re vért izzadva leltünk megoldást.
|
| Előzmény: [2194] Csimby, 2007-08-02 00:56:23 |
|
| [2195] Lóczi Lajos | 2007-08-02 02:14:23 |
 A számítógépbe csak beírom, hogy DSolve, lásd pl. itt.
Amúgy meg a legyegyszerűbb módszer a következő. (Nem írok se vektort, se mátrixot.)
Adott tehát az y'=y+2z és z'=-y+3z rendszer. Kifejezed pl. az elsőből z-t y-nal és beírod a másodikba. Kapsz egy valós, homogén, lineáris, másodrendű egyenletet y-ban. A karakterisztikus polinom két gyöke  1,2=2 1,2=2 i, vagyis (használva az Euler-formulát) két lineárisan független megoldás az i, vagyis (használva az Euler-formulát) két lineárisan független megoldás az 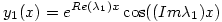 és és 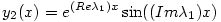 . Emiatt y(x)=c1.y1(x)+c2.y2(x). Innen z(x) már csak egy szimpla visszahelyettesítés. (Láthatod, hogy nem betű szerint ugyanaz jött ki, mint amit a gép adott, de könnyen látszik, hogy c1 és c2-t alkalmasan átnevezve mégsem kaptunk mást.) . Emiatt y(x)=c1.y1(x)+c2.y2(x). Innen z(x) már csak egy szimpla visszahelyettesítés. (Láthatod, hogy nem betű szerint ugyanaz jött ki, mint amit a gép adott, de könnyen látszik, hogy c1 és c2-t alkalmasan átnevezve mégsem kaptunk mást.)
|
| Előzmény: [2193] Willy, 2007-08-02 00:35:58 |
|
|
| [2193] Willy | 2007-08-02 00:35:58 |
 Megkérhetnélek mindkettőtöket, hogy mutassátok meg, ti egész pontosan hogyan oldanátok meg a feladatot (a gépesnek is nagyon örülnék). (Ugyanis se diffegyenletet nagyon, se komplex függvénytant nem tanultam még suliban, csak saját szakállamra; és nem nagyon látom át a helyzetet.)
Előre is köszönöm :-)
|
| Előzmény: [2192] Lóczi Lajos, 2007-08-02 00:20:51 |
|
|
| [2191] Cckek | 2007-08-01 21:26:43 |
 Bocs Willy, az előző hozzászolásomban a mátrix:
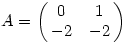 . .
Elfelejtettem, hogy megváltoztattam a feladat adatait:)
|
|
| [2190] Cckek | 2007-08-01 21:19:55 |
 Helló Willy.
Igen, valami ilyesmi jött ki nekem is vizsgán, bár kissé bonyolultabban. 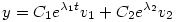
Ahol  1=-1+i, 1=-1+i, 2=-1-i sajátértékek és 2=-1-i sajátértékek és
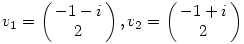 sajátvektorok. Na ezt kéne valóssá alakítani. sajátvektorok. Na ezt kéne valóssá alakítani.
|
| Előzmény: [2186] Willy, 2007-08-01 02:36:51 |
|
| [2189] Hajba Károly | 2007-08-01 21:14:07 |
 De ez ugye csak nem-kilépő? Mert nálam a visszazárt annyit tesz, hogy a kiindulási pontba zár vissza. Azaz nem lehet a gráf egyetlen pontja sem páratlan élű, csak páros. Nálam. :o)
Ha a bal alsóból [1,1] indulsz, akkor csak a [4,4]-be érkezhetsz. Erre én is ráleltem, csak én nem hosszabbítottam meg a már meglévő vonalig. Az [1,1]-be kellene vissza is érkezni.
|
| Előzmény: [2188] Csimby, 2007-08-01 20:36:28 |
|
|
|
| [2186] Willy | 2007-08-01 02:36:51 |
 Szia Cckek!
Nem vagyok valami penge a diffegyenltekből, de megnéztem egy próbafüggvényre:
Legyen
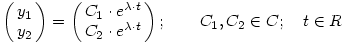
(Érzésem szerint ez a próbafüggvény minden megoldást vissza fog adni.)
Végezzük el a mátrixszorzást és a próbafüggvény deriválását is:
![\left(\matrix{y_1\cr y_2\cr}\right)'= \left( \matrix{C_1\cdot \lambda \cdot e^{\lambda\cdot t}\cr C_2\cdot \lambda \cdot e^{\lambda\cdot t}\cr} \right)= \left[\matrix{1&2\cr -1&3\cr}\right]\cdot \left( \matrix{C_1\cdot e^{\lambda\cdot t}\cr C_2\cdot e^{\lambda\cdot t}\cr} \right)= \left(\matrix{(C_1+2C_2)\cdot e^{\lambda\cdot t}\cr (-C_1+3C_2)\cdot e^{\lambda\cdot t}\cr}\right)](keplet.cgi?k=1B896813E872F5CC)
Ebből kapunk egy három paraméterrel rendelkező, egyváltozós, két egyenletből álló egyenletrendszert:
C1. =C1+2C2 =C1+2C2
C2. =-C1+3C2 =-C1+3C2
Elsőből kifejezzük C2-t, beírva a másodikba és rendezve, kapjuk:
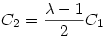
0=C1.( 2-4. 2-4. +5) +5)
1) Ezek alapján C1=C2=0 és   R azaz R azaz 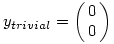
2) Avagy,  1,2=2 1,2=2 i, C1 i, C1 R és R és 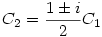 , azaz , azaz
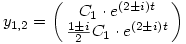
A három megoldás...
|
| Előzmény: [2183] Cckek, 2007-07-29 20:18:25 |
|
|
|
| [2183] Cckek | 2007-07-29 20:18:25 |
 Adott az 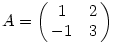 . Oldjuk meg az y'=Ay differenciálegyenletet. . Oldjuk meg az y'=Ay differenciálegyenletet.
|
|
|
| [2181] epsilon | 2007-07-29 14:01:01 |
 Helló Cckek, a Te szimpatikus feladatodra akartam választ adni, de egy sorral lennebb klickeltem, így a Doom nickre hívatkozik a válasz!
|
|
| [2180] epsilon | 2007-07-29 13:58:09 |
 Helló! Ha jól számoltam akkor a tört abszolútértéke 1/3, nem de? Pl. végezzük el a z=3+z' transzformációt, így a feltétel alapján abs(z')=1 ezért jelölje z"=konjugált(z). Így 1/z'=z" továbbá ha az abs[(4-z)/(4+z)]=E akkor E=abs[(3z'+1)/(3z'+9)]=1/3*A ahol A=abs[(3z'+1)/(z'+3)]. Most a tört számlálóját és nevezőjét is tagonkénz osztva z'-tel, a konjugálás tulajdonsága alapján azt kapjuk, hogy A=1/A adódik, és A>0 tehát A=1, így E=1/3.
|
| Előzmény: [2177] Doom, 2007-07-28 19:57:48 |
|
| [2179] epsilon | 2007-07-29 13:10:22 |
 Kösz Doom! Az még vettem észre, azzal valóban jobban be lehet osztani csoportokra, de valójában azt a keresési módszereket hiányolom, amikor konkrét szóra, stb. lehetne rákeresni, de gondolom, hogy ezt nem könnyű megvalósítani, mert már megtették volna, nem Én találnám fel a spanyolviaszt! Üdv: epsilon
|
| Előzmény: [2176] epsilon, 2007-07-28 19:35:48 |
|
|
| [2177] Doom | 2007-07-28 19:57:48 |
 A hozzászólások felett jobb felül: hány hsz legyen a lapon és rendezze a legöregebbel kezdve... innen már te is ki tudod egyszerűen számolni, hogy melyik sorszám hányas lapra esik... ;)
Ha olyan gyorsabb keresésre gondoltál, ami kulcsszavak alapján működne, az szerintem is hasznos lenne.
|
| Előzmény: [2176] epsilon, 2007-07-28 19:35:48 |
|
| [2176] epsilon | 2007-07-28 19:35:48 |
 Kedves Károly! Hát így sorszámszerint valahogy könnyebb volt betájolni, de tényleg kár, ha nem létezik olyan keresés, hogy ha beírod az adott hsz számát, akkor oda vigyen...de hát meglehet, hogy csak Nekem hiányzik. Mindenképpen kösz a segítséget! Üdv: epsilon
|
|
| [2175] epsilon | 2007-07-28 19:27:14 |
 Kedves Károly! Kösz, de nem találok valami szapora keresési lehetőséget, mint pl. a Neten, itt látom a [1. oldal] [2.oldal][3. oldal][4. oldal]...lehetőségeket, de a hozzászólások hosszából hogyan lehet megsaccolni, hogy melyikbe esik pl. 99. hozzászólás. Kár, hogy nem találtam, vagy nem található (?) szaporább keresési lehetőség! De addig is bogarászok! Üdv: epsilon
|
|
|
| [2173] epsilon | 2007-07-28 13:40:36 |
 Kedves Károly! Nem igazán szoktam döngetni ;-) meg a Fórumot sem ismerem annyira részleteiben, nem is járok régóta és túl gyakran ide, úgyhogy szerintem ülhet ott a valahol ahol van, mert biztosan nem találok rá, inkább majd szórakozásból megpróbálok magam rájönni. Üdv: epsilon
|
| Előzmény: [2170] epsilon, 2007-07-28 07:11:46 |
|
| [2172] Hajba Károly | 2007-07-28 13:28:21 |
 Üdv!
Közben az n=7 12 vonalasra találtam mégegy szigorú feltételű megoldást, így már 3-at is ismerek.
De a Csimby jelezte n=5 8 vonalasra még nem leltem rá, sőt még n=6 10 vonalast sem találtam.
|
| Előzmény: [2167] epsilon, 2007-07-27 18:13:42 |
|
| [2171] Hajba Károly | 2007-07-28 08:22:52 |
 Kedves epsilon!
Kicsit rejtélyes leszek. Nyitott kapukat döngetsz. Ti. a megoldások megtalálhatóak itt a KöMaL fórumon ... valahol. Csak meg kell keresni őket. Tudom, nem lesz nehéz, sok sikert hozzá. S ha meglelted, berakok még néhány nem-kilépő megoldást n=5, 6 tartományból.
:o)
|
| Előzmény: [2170] epsilon, 2007-07-28 07:11:46 |
|
| [2170] epsilon | 2007-07-28 07:11:46 |
 Kedves Károly! A jelzett lehetőségekről bemutatnál rajzot is, hátha további lehetőségeket tartogat? Üdv: epsilon
|
|
|
| [2168] Csimby | 2007-07-28 00:08:50 |
 Szia! Köszi az ábrákat! Az én algoritmusom most veszem észre, hogy mégsem jó, mert noha megfelelő számú szakaszból áll, az egyiket 2 részletben húzom be az pedig csalás (1 behúzással nem lehet mert van benne egy 3-fokú csúcs így muszáj abból indulni). Amúgy azt akartam, hogy az n=5-re talált "nem kilépő" megoldásomat (amit még nem akarok lerajzolni) L-alakban két szakasszal kibővítem és egy régi szakaszt meghosszabítok, ekkor n=6 egy megoldását kapom és ez folytatható is lenne, csak hát mégsem jó.
|
| Előzmény: [2167] epsilon, 2007-07-27 18:13:42 |
|
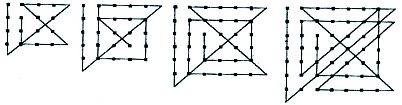
| [2167] epsilon | 2007-07-27 18:13:42 |
 A 328-as feladat kapcsán a következő biztos: n×n pont összeköthető 2n-2 szakaszból álló töröttvonallal, a kért feltétellel. Szemléltetés és algoritmus kialakítása végett itt egy "kép" egy pár esettel:
|
 |
| Előzmény: [2156] Csimby, 2007-07-26 23:20:32 |
|
| [2166] Hajba Károly | 2007-07-27 12:47:46 |
 A spirál alatt azt értem, hogy a mátrixot kivülröl körkörösen, majd mindig befelé haladva folyamatosan felfűztem. Ehhez, amint jól látod 1-gyel több vonal kell. Anno így határoztam meg a szükséges lépésszámot, azaz a spirálban található vonalak számából elvettem egyet. Persze később a képletet is meghatároztam. :o)
---
Az n=5 nemkilépő és visszazárón akkor elkezdek gondolkodni.
|
| Előzmény: [2164] Csimby, 2007-07-27 09:52:47 |
|
|
| [2164] Csimby | 2007-07-27 09:52:47 |
 Most látom csak hogy ez a feladat egyszer mennyire ki lett már vesézve (pl. 39.feladat), Spirálozás alatt amúgy azt érted hogy mindig az egyel kisebb oldalhosszú négyzet megoldásából állítjuk elő a következőt? Vagy mire gondolsz? Mert ugye ha csak úgy felspirálozzuk a pontokat, akkor az 1-gyel több szakasz.
|
| Előzmény: [2162] Hajba Károly, 2007-07-27 08:33:24 |
|
|
| [2162] Hajba Károly | 2007-07-27 08:33:24 |
 A "spirálozást" még anno eljátszottam, mikor a 7*7-es megoldását kerestem. E témakörben az lehet még érdekes, hogy melyik legkisebb n-nél lehet már megoldást találni, (1)hogy vissza lehessen zárni, (2)hogy ne lépjen ki a törtvonal a külső pontokon ill. (1) és (2) egyszerre. n=4-re már lehet zárt görgét találni, n=5-re pedig nem kilépőt. A kettő együtt eddig még az ismert n=7.
|
| Előzmény: [2161] Csimby, 2007-07-27 01:31:34 |
|
|
|
| [2159] Hajba Károly | 2007-07-27 00:54:05 |
 Szerintem az általánosító képlet 2(n-1), azaz a mátrix pontjait spirálisan 2(n-1)+1 szakaszból álló törtvonal segítségével tudjuk felfűzni.
S így ezen feltételekkel szerintem már megoldhatóak. Lásd n=7 esetében már két szigorításal is. (nincs kilépés és visszazár)
|
| Előzmény: [2148] Csimby, 2007-07-25 18:03:01 |
|
|
|
| [2156] Csimby | 2007-07-26 23:20:32 |
 Hát ez nagyon ügyes, gratulálok!
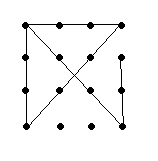
328.-ban az a feladat pl. n=4-re, hogy az ábrán látható 16 ponthoz megadható e egy 5 szakaszból álló töröttvonal amit a "ceruza felemelése nélkül" meg tudunk rajzolni és mind a 16 ponton átmegy. n=3-ra van ilyen 4-vonalból ez az ábráról leolvasható. Valaki azt állította egy ismerősömnek, hogy minden n-re van ilyen töröttvonal, de szerintem már n=4-re sincs. (pl. az ábrán 2 pont kimarad)
|
 |
| Előzmény: [2154] nadorp, 2007-07-26 21:08:23 |
|
|
| [2154] nadorp | 2007-07-26 21:08:23 |
 Másképp számoltam, a módszert még egyetemen hallottam egy szenzációs tanáromtól. Legyen 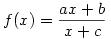 és tekintsük f(x) fixpontjait, azaz az f(x)=x egyenletet, x2+(c-a)x-b=0. Ha ennek két ( akár komplex) gyöke x1,x2, akkor és tekintsük f(x) fixpontjait, azaz az f(x)=x egyenletet, x2+(c-a)x-b=0. Ha ennek két ( akár komplex) gyöke x1,x2, akkor
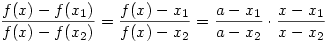 ( legyen ez a 327/a/a feladat :-), valamint ( legyen ez a 327/a/a feladat :-), valamint
x1+x2=a-c és x1x2=-b
Indukcióval azonnal adódik, hogy 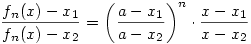 . .
Ha most a,x1,x2 értékét úgy választjuk meg, hogy
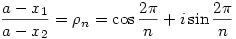 ( az első primitív n-dik egységgyök), akkor fn(x)=x adódik. Ha még x1=x2konjugált ( nem tudom a felső vízszintes vonalat TeX-ben :-), akkor x1,x2 lehetnek egy másodfokú egyenlet komplex gyökei. ( az első primitív n-dik egységgyök), akkor fn(x)=x adódik. Ha még x1=x2konjugált ( nem tudom a felső vízszintes vonalat TeX-ben :-), akkor x1,x2 lehetnek egy másodfokú egyenlet komplex gyökei.
Könnyen látható, hogy a=1, x1=- n , x2=- n , x2=- n-1 jók lesznek, innen b és c értéke a fentiek alapján könnyen számolható. n-1 jók lesznek, innen b és c értéke a fentiek alapján könnyen számolható.
|
| Előzmény: [2153] Csimby, 2007-07-26 19:17:17 |
|
| [2153] Csimby | 2007-07-26 19:17:17 |
 Köszi! Hogyha a törtfüggvénybe n-szer behelyettesítem önmagát, majd egyenlővé teszem ezt x-vel. a=1, b=-1-et helyettesítek és egyoldalra rendezem, akkor ebből kiemelhető lesz c-egy polinomja, amit megoldok hogy mikor 0. Így jön ki c-re az amit a megoldásban írtál? (n=3-ra ez működik, de 4-re nem szenvedtem végig)
Más: 328.-ra szerintem nemleges a válasz.
|
| Előzmény: [2152] nadorp, 2007-07-26 12:03:32 |
|
|
|
| [2150] nadorp | 2007-07-26 10:02:25 |
 A 327/a feladatra szerintem pozitív a válasz, azaz minden n-re van olyan elsőfokú racionális törtfüggvény ( 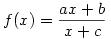 alakú), melyre f(n)=x ( ez most kompozíció és nem deriválás :-) alakú), melyre f(n)=x ( ez most kompozíció és nem deriválás :-)
|
| Előzmény: [2148] Csimby, 2007-07-25 18:03:01 |
|
|
| [2148] Csimby | 2007-07-25 18:03:01 |
 Előző feladatomra sajnos senki se reagált :-( Itt van pár új.
328.feladat A [2].hozzászólásban szereplő 2.feladat általánosítható-e n×n-es négyzetre és n+1 egymáshoz csatlakozó szakaszra. Már n=4-re is kíváncsi lennék hogy mit mondtok.
329.feladat Két Sudoku -táblázat távolsága legyen azon mezők száma ahol eltérnek egymástól. Milyen távolságok fordulhatnak elő két táblázat között.
Érdekes kérdés még hogy hány különböző Sudoku-táblázat van, illetve, hogy legkevesebb hány mezőt lehet úgy megadni, hogy legyen egyértelmű megoldás. De ezekről sajnos azt találtam hogy igen nehezek lehetnek.
|
|
|
| [2146] Lajos Arpad | 2007-07-21 10:41:18 |
 328. feladat Vegyük a kôvetkezô mértani haladványt: 1, x, x*x... x természetes szám és nagyobb mint 1, n természetes sám S(n)=1+x+...+(x) az n-dik hatványon Bizonyítsuk be, hogy: S(n)/(x-1) természetes szám <=> (n+1)/(x-1) természetes szám.
|
|
|
|
|
| [2142] Cckek | 2007-07-17 22:37:13 |
 A nagy meleg miatt, megaztán nyaralás okán elég hulla a forum, itt van egy frissitő:
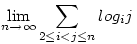
|
|
| [2141] Csimby | 2007-07-07 04:02:03 |
 327.feladat Az f:R R fv. n-edik hatványa legyen fn=fo...of - n db f összekomponálva (tegyük fel, hogy Rfk R fv. n-edik hatványa legyen fn=fo...of - n db f összekomponálva (tegyük fel, hogy Rfk Dfk+1, k Dfk+1, k 1 vagy k 1 vagy k 0 - ez esetben f0:=id, még nem tudom hogy lesz érdekesebb a feladat 0-val vagy 1-gyel. Megj.: Ha k 0 - ez esetben f0:=id, még nem tudom hogy lesz érdekesebb a feladat 0-val vagy 1-gyel. Megj.: Ha k 0 akkor f az egész R-en értelmezett és így fn=id-ből következik, hogy f összes hatványa is egész R-en értelmezett). Egy f R 0 akkor f az egész R-en értelmezett és így fn=id-ből következik, hogy f összes hatványa is egész R-en értelmezett). Egy f R R fv. rendje legyen az a legkisebb n pozitív egész, melyre fn=id. R fv. rendje legyen az a legkisebb n pozitív egész, melyre fn=id.
a. feladat Keressünk minden n-re n-rendű f:R R függvényt. R függvényt.
A Cckek által [2116]-ban kitűzött feladatban pl. az 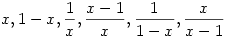 függvények az R-{0,1} értelmezési tartományban csoportot alkotnak a kompozícióra nézve az R függvények az R-{0,1} értelmezési tartományban csoportot alkotnak a kompozícióra nézve az R R fv.-ek terében. Ebben a csoportban R fv.-ek terében. Ebben a csoportban 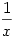 rendje 2, rendje 2, 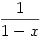 rendje 3, a csoport 6 elemű, így ez a csoport izomorf S3-mal. rendje 3, a csoport 6 elemű, így ez a csoport izomorf S3-mal.
b. feladat Mely G csoportoknak adható meg ilyen R R fv.-ekkel reprezentációja? (keressünk ilyen reprezentációkat) Megj.: Az a. feladat tehát azt kéri, hogy adjuk meg minden n-re Zn egy reprezentációját és n=2,3-ra már mutattunk példát, igaz egyik sem volt az egész R-en értelmezve, kérdés: van-e ilyen?. R fv.-ekkel reprezentációja? (keressünk ilyen reprezentációkat) Megj.: Az a. feladat tehát azt kéri, hogy adjuk meg minden n-re Zn egy reprezentációját és n=2,3-ra már mutattunk példát, igaz egyik sem volt az egész R-en értelmezve, kérdés: van-e ilyen?.
u.i.: Most egy hétig nem leszek, pedig kíváncsi vagyok miket fogtok írni, mindenesetre még én sem gondolkoztam a feladatokon, csak a [2116]-ban kitűzött feladat kapcsán vetődtek fel bennem ezek a kérdések.
|
|
|
|
| [2138] Csimby | 2007-07-05 17:33:57 |
 Szia!
2/A-ban card a számosságot jelenti? És ha igen, akkor abból hogy ez alef0 miért következik, hogy Z? (Pl. Q nem izomorf Z-vel hiszen nem ciklikus)
|
| Előzmény: [2137] Cckek, 2007-07-05 10:42:17 |
|
| [2137] Cckek | 2007-07-05 10:42:17 |
 Természetesen ki kell zárni a G={0} esetet. Először bebizonyítjuk, hogy G nem korlátos. Legyen
g G,g G,g 0.Mivel G csoport,(g 0.Mivel G csoport,(g G G -g -g G) vehetjük g>0 és ng G) vehetjük g>0 és ng G minden n G minden n N esetén. Ekkor az arkhimédészi axioma értelmében minden r N esetén. Ekkor az arkhimédészi axioma értelmében minden r R-re van olyan n R-re van olyan n N melyre ng>r. Tehát G nem korlátos, és G nem véges. N melyre ng>r. Tehát G nem korlátos, és G nem véges.
1. Ha G-nek nincs torlodási pontja mivel G zárt és nem korlátos, ugyanakkor nG G igy G megszámlálható végtelen sok izolált pontból áll, tehát izomorf Z-vel. G igy G megszámlálható végtelen sok izolált pontból áll, tehát izomorf Z-vel.
2. Ha x G torlodási pontja G-nek, akkor ha V környezete x-nek,(V végtelen sok pontot tartalmaz a G-ből)akkor minden y G torlodási pontja G-nek, akkor ha V környezete x-nek,(V végtelen sok pontot tartalmaz a G-ből)akkor minden y G esetén (y-x)+V környezete y-nak (és végtelen sok pontot tartalmaz a G-ből), tehát y szintén torlodási pont. Tehát ebben az esetben G minden pontja torlodási pont. Két lehetségünk van: G esetén (y-x)+V környezete y-nak (és végtelen sok pontot tartalmaz a G-ből), tehát y szintén torlodási pont. Tehát ebben az esetben G minden pontja torlodási pont. Két lehetségünk van:
A. G egyetlen pontjának sincs G-beli környezete. Ekkor G minden pontjának a környezetei megszámlálható végtelen sok pontot tartalmaznak G-ből, tehát cardG= 0 igy izomorf Z vel. 0 igy izomorf Z vel.
B. Létezik x G úgy, hogy V=(x- G úgy, hogy V=(x- ,x+ ,x+ ) ) G. Ekkor V-x=(- G. Ekkor V-x=(- , , ) ) G és az archimédészi axioma értelmében G és az archimédészi axioma értelmében
(-n ,n ,n ) ) G, G, n n N tehát G=R N tehát G=R
|
| Előzmény: [2133] Csimby, 2007-07-03 16:56:32 |
|
|
|
|
|
|
| [2131] HoA | 2007-07-03 11:24:07 |
 Igazad van. Sőt még abban is tévedtem, hogy x1,x2 tetszőleges multiplicitással szerepelhet. A valós együtthatós kikötés miatt ez nem igaz, csak párokban léphetnek fel.
Este végignéztem a hat gyök össszes párosításából adódó megoldásokat. Szerintem csak a már ismert 1/2, 2, -1, x1 és x2 értékeket kapjuk. Így aztán könnyen lehet, hogy csak az általad mondottakból adódó (x-x1)(x-x2)(x-1/2)(x-2)(x+1) polinom és a [2129] -beli P(x) a megoldás.
|
| Előzmény: [2130] Csimby, 2007-07-02 22:59:08 |
|
|
| [2129] HoA | 2007-07-02 16:53:25 |
 Szerintem nem kell túlbonyolítani. Odáig világos, hogy a 6 gyökhely 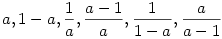 . Mivel a polinom csak ötödfokú, szükségképpen vannak köztük egyenlőek. Szépen végig kell nézni, mi adódik ha az egyes párokat egyenlővé tesszük. Például a = 1-a -ból a=1/2 és . Mivel a polinom csak ötödfokú, szükségképpen vannak köztük egyenlőek. Szépen végig kell nézni, mi adódik ha az egyes párokat egyenlővé tesszük. Például a = 1-a -ból a=1/2 és 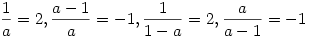 És itt nem baj, hogy további egybeeső gyökök vannak. A megoldás így írható: És itt nem baj, hogy további egybeeső gyökök vannak. A megoldás így írható: 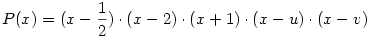 , ahol u és v egymástól függetlenül felveheti az 1/2, 2 és -1 értékeket. A további polinomokat a többi pár egyenlővé tételével keressük, és elhagyjuk az ismétléseket. Az , ahol u és v egymástól függetlenül felveheti az 1/2, 2 és -1 értékeket. A további polinomokat a többi pár egyenlővé tételével keressük, és elhagyjuk az ismétléseket. Az 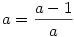 választással adódik a már szerepelt választással adódik a már szerepelt 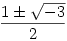 páros, ekkor valóban csak ez a két gyök van, jelöljük őket x1ésx2 vel, a polinom így P(x)=(x-x1).(x-x2).(x-u).(x-v).(x-z), ahol megintcsak u,v, és z x1vagyx2. És így tovább, ha van még... páros, ekkor valóban csak ez a két gyök van, jelöljük őket x1ésx2 vel, a polinom így P(x)=(x-x1).(x-x2).(x-u).(x-v).(x-z), ahol megintcsak u,v, és z x1vagyx2. És így tovább, ha van még...
|
| Előzmény: [2125] jonas, 2007-07-02 15:19:18 |
|
|
|
|
| [2125] jonas | 2007-07-02 15:19:18 |
 Egyébként a feladat azért trükkös, mert elindulhat valaki a rossz irányba is, hogy felteszi, hogy az öt gyök különönböző, és nem jut eszedbe, hogy 1-1/(1-1/(1-1/a))=a.
Ekkor gondolhat arra, hogy párba állítja a gyököket úgy, hogy a párja 1-a legyen, és mivel az öt páratlan, ezért biztosan gyök az 1/2 mert csak az párja önmagának, vagy hogy párba állítjuk a-t 1/a-val, és akkor biztosan gyök 1 és -1 közül az egyik.
Vagy arra is gondolhat (szintén ha az összes gyök különböző), hogy ha minden a gyökhöz 1-a is gyök, akkor a gyökök összege 5/2 így az x4 együtthatója -5/2, valamint hasonlóan a gyökök szorzata 1 így a konstans tag 1.
|
|
| [2124] jonas | 2007-07-02 15:11:54 |
 Na nézzük. Ha a=1-a, akkor a=1/2 és a gyökök 1/2,2,-1. Ha a=1/a akkor vagy a=-1 ami az előző eset, vagy a=1 jönne ki, de az nem jó, mert akkor az 1/0 is gyöke lenne a polinomnak.
Ha a=1/(1-a), akkor 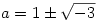 és ilyenkor csak két gyök van, mert a=1/(1-a)=(a-1)/a és 1-a=1/a=a/(a-1). és ilyenkor csak két gyök van, mert a=1/(1-a)=(a-1)/a és 1-a=1/a=a/(a-1).
Ezzel ki is merítettük az összes lehetőséget a gyökökre nézve, de a polinomokat nem adtuk meg.
|
| Előzmény: [2122] Csimby, 2007-07-02 13:53:58 |
|
|
|
|
|
|
| [2118] Csimby | 2007-07-02 13:37:44 |
 (reciprok képzés, 1-x, nem vezet ki közülük, viszont ezeknek mind szerepelnie kell) Kéne még vacakolni hogy mi van ha egybeesik pár. De úgy emlékszem algerba gyakorlaton volt valami hasonló Galois elmélet keretein belül. Majd ha végeztem a diffegy vizsgával és lesz időm megkeresem :-)
|
| Előzmény: [2117] Csimby, 2007-07-02 13:31:30 |
|
|
| [2116] Cckek | 2007-07-02 12:48:26 |
 Szép:) Amúgy ezek második fokozati vizsgakérdések itt Romániában. Itt van még egy ha érdekel valakit:
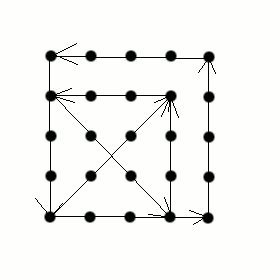
Határozzuk meg azokat az ötödfokú valós együtthatós P(X) polinomokat, melyeknek a domináns együtthatójuk 1 és, ha a gyöke P-nek akkor 1-a illetve 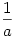 is gyöke P-nek. is gyöke P-nek.
|
|
| [2115] Lóczi Lajos | 2007-07-02 11:04:13 |
 A feladatban határozatlan integrálok szerepelnek: ha a két integrációs állandót különbözőnek választjuk, elég nehéznek tűnik a kérdés. Legyenek tehát egyenlőek.
Az egyenletet f-re rendezve látjuk, hogy f deriválható a pozitív és a negatív félegyenesen. Deriválva az egyenletet egy differenciálegyenletet kapunk, melynek megoldásai
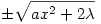
alakúak, valamely a 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen. 0 állandóval. Most csak a pozitív előjel jön szóba. A feladat megoldásai lesznek tehát az olyan f függvények, amelyek x>0 és x<0 esetén a fenti képlettel vannak megadva, esetleg más-más a állandóval a pozitív és a negatív részen.
|
| Előzmény: [2113] Cckek, 2007-07-01 19:42:18 |
|
| [2114] Cckek | 2007-07-02 09:19:08 |
 Határozzuk meg az összes morfizmust (Q,+) és (Sn,o) között.
|
|
|
|
|
| [2110] Sirpi | 2007-06-22 23:50:30 |
 Na jó, akkor lecsapom :-)
Pont elolvastam a feladatot, majd a vihar miatt jött egy 2 órás áramszünet, azalatt volt időm (többek közt ezt is) végiggondolni.
Tehát f(f(n))=f(n)+n és f(1)=2.
A Fibonacci-számokon végigugrálva az embernek elég hamar előjön az a sejtése, hogy ![f(n) = [\frac{\sqrt 5+1}2 n + \frac 12]](keplet.cgi?k=50BD69C500659BDD) , vagyis a függvény lineáris , vagyis a függvény lineáris 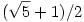 -es szorzóval, egészre kerekítve. -es szorzóval, egészre kerekítve.
És hogy ez miért jó? Legyen 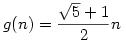 , vagyis a kerekítés nélküli függvény. Erre nyilván , vagyis a kerekítés nélküli függvény. Erre nyilván 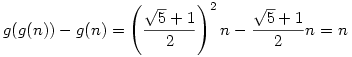
Másrészt minden n-re |f(n)-g(n)|<1/2, vagyis n-1<f(f(n))-f(n)<n+1, és mivel a különbség egész, ezért csak n lehet. Ezen kívül 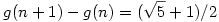 , vagyis , vagyis 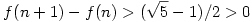 , így f(n+1)-f(n) , így f(n+1)-f(n) 1. 1.
|
| Előzmény: [2109] Cckek, 2007-06-22 19:38:21 |
|
| [2109] Cckek | 2007-06-22 19:38:21 |
 Felhívnám a tisztelt forumozók figyelmét, hogy a 2089-es hozzászolásomban kitűzött gyönyörűszép feladat még mindig megoldatlan:)
|
|
| [2108] Sirpi | 2007-06-21 11:50:54 |
 Szép elemzés!
Azért leírom azt is, hogy én mire jutottam. Talán kicsit egyszerűbb becsléseket használok, valamint semmilyen függvényvizsgálatra nincs szükség.
Legyen y:=n+x
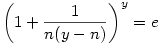
És itt, mikor 1/y-edik hatványra emelem mindkét oldalt:
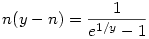
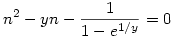
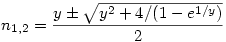
A két gyök közül az egyik lesz n, a másik xn. Az egyik gyök (a minuszos) 1 körül van, nézzük meg ezt alaposabban. Feltételezve, hogy y nagy, e1/y=1+1/y+1/(2y2)+O(1/y3), ahonnan
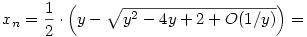
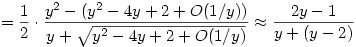
Ez pedig éppen az 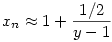 becslést adja, ahonnan szintén látszik az 1/2-es határérték. Viszont kihasználtam, hogy ha n becslést adja, ahonnan szintén látszik az 1/2-es határérték. Viszont kihasználtam, hogy ha n  , akkor y , akkor y  , ezt még annyival meg kell támogatni, hogy mivel a két gyök összege y, ezért valamelyik a kettő közül legalább y/2, válasszuk ezt n-nek, a másikat pedig xn-nek. , ezt még annyival meg kell támogatni, hogy mivel a két gyök összege y, ezért valamelyik a kettő közül legalább y/2, válasszuk ezt n-nek, a másikat pedig xn-nek.
* * *
Mindamellett azért is írtam le ezt az egészet, mert az az érdekes dolog látszik belőle, hogy ha nem n és xn lenne a feladatban, hanem x és f(x), akkor bejönne egy új gyök, hiszen az első lépésnél, a hatványozásnál az alap lehet épp negatív is, ha a kitevő (y) páros egész szám. Ekkor:
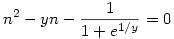
Ennek pedig egy pozitív (n), és egy negatív (xn) gyöke van. Viszont az sose fordulhat elő egyszerre, hogy y páros egész és n is egész, de ha n tetszőleges valós szám lehet, ami tart a végtelenbe, akkor valóban kapunk egy új gyököt:
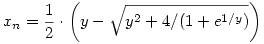
Itt most e1/y 1 triviális becslést alkalmazva 1 triviális becslést alkalmazva
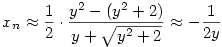
Szóval ha n nem feltétlen egész, akkor van egy másik (negatív) sorozat is xn-re (ilyenkor az alap -1 közelében van).
|
| Előzmény: [2106] Lóczi Lajos, 2007-06-21 03:16:23 |
|
|
| [2106] Lóczi Lajos | 2007-06-21 03:16:23 |
 Használjuk fel a pontosabb x-x2/2<ln (1+x)<x-x2/2+x3/3 egyenlőtlenséget. Ebből arra következtethetünk, hogy xn az
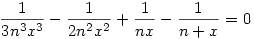
és az
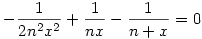
egyenletek (1-hez közeli) gyökei között van. Ez egy másod- és egy harmadfokú egyenlet, a megoldóképleteik felírhatók. Az ezekben szereplő négyzet- és köbgyököket a binomiális tétellel lehet sorbafejteni, amiből végül megkapjuk, hogy mind az alsó-, mind a felső becslése xn-nek 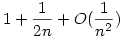 , ha n , ha n  . .
|
| Előzmény: [2104] Lóczi Lajos, 2007-06-21 01:34:29 |
|
|
| [2104] Lóczi Lajos | 2007-06-21 01:34:29 |
 A kérdéses xn sorozat az 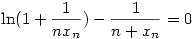 egyenlet gyöke. egyenlet gyöke.
Bizonyos mennyiségű számolással (első- és második deriváltak vizsgálata, határérték a 0-ban és a végtelenben, stb.) belátható, hogy ennek az egyenletnek minden, elég nagy n-re (pl. n>10) csak 1 gyöke van, az is 1 és pl. 2 között. Ez azért segít, mert ekkor használható az 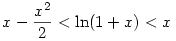 egyenlőtlenség (0<x<1). Így az eredeti egyenlet xn gyöke beszorítható két egyszerű egyenlet gyöke közé. Ebből kapjuk pl., hogy egyenlőtlenség (0<x<1). Így az eredeti egyenlet xn gyöke beszorítható két egyszerű egyenlet gyöke közé. Ebből kapjuk pl., hogy
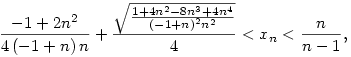
ami maga után vonja, hogy elég nagy n-ekre
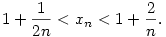
Tehát az (xn-1)na sorozatnak csak a=1 esetén lehet véges, nemnulla limesze (ha egyáltalán létezik).
Finomabb ötleteket fog igényelni annak kiderítése, hogy (xn-1)n melyik pozitív számhoz tart.
|
| Előzmény: [2103] Lóczi Lajos, 2007-06-19 22:38:34 |
|
|
|
|
|
|
| [2098] lorantfy | 2007-06-19 11:59:09 |
 Kedves Lajos!
Én úgy gondolkodtam, hogy az a és b megadásához minket az xn sorozat csak határértékben érdekel, vagyis nyugodtan helyettesíthető az 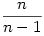 sorozattal, különben első egyenlet nem lenne igaz. sorozattal, különben első egyenlet nem lenne igaz.
Az 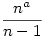 határértéke pedig a<1-nél 0, a=1-nél 1, a>1-nél végtelenbe megy. határértéke pedig a<1-nél 0, a=1-nél 1, a>1-nél végtelenbe megy.
|
| Előzmény: [2095] Lóczi Lajos, 2007-06-19 00:18:52 |
|
|
|
|
|
|
|
| [2091] jonas | 2007-06-18 22:07:31 |
 f(f(x))-es függvényegyenletből csak egy jut eszembe: f:R R differenciálható, mindenütt pozitív, f'(x)=f(f(x)). (Úgy emlékszem, nincs megoldása, de utánanézhetek, ha kell.) R differenciálható, mindenütt pozitív, f'(x)=f(f(x)). (Úgy emlékszem, nincs megoldása, de utánanézhetek, ha kell.)
|
| Előzmény: [2089] Cckek, 2007-06-18 18:33:49 |
|
|
| [2089] Cckek | 2007-06-18 18:33:49 |
 Egy nagyon érdekes feladattal találkoztam a minap. Létezik-e olyan f:N N függvény melyre f(1)=2, N függvény melyre f(1)=2,
f(f(n))=f(n)+n, és f(n)<f(n+1)?
|
|
|
| [2087] Cckek | 2007-06-11 21:06:11 |
 Valóban, bár ennek a bizonyítása nem is olyan egyszerű.:)
|
|
|
| [2085] Cckek | 2007-06-10 09:40:08 |
 Az xn sorozat a következőképpen adott:
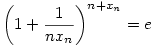 Határozzuk meg az a,b Határozzuk meg az a,b R számokat úgy hogy R számokat úgy hogy
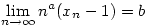
|
|
| [2084] psbalint | 2007-06-06 14:39:15 |
 jah...most nézem csak...szóval akkor 1706-1715-ig :)
|
|
| [2083] psbalint | 2007-06-06 14:37:26 |
 lásd az 1706-1715., illetve a 349. hozzászólást :)
|
|
| [2082] s_fecko | 2007-06-05 21:06:21 |
 77. feladat: (Felesben legel e kecske) Egy kecskepásztor egyik nap egy kerek legelőre vitte ki egyetlen kecskéjét legelni. De hogy ne kelljen másnap újabb legelő után nézni, úgy szeretné kikötni, hogy csak a legelő felét tudja a kecskéje lelegelni. A karót a legelő szélén verte le. Milyen hosszúra kell a kecske kötelékét engednie?
Megköszönném ha valaki e-mailben elküldené a megoldást részletezve! Mivel a 349-es hozzászólásban megvan a megoldás, de az számomra átláthatatlan. Még amatőr vagyok, de próbálkozom :) Ha esetleg valaki csak simán elmagyarázná a megoldás menetét annak örülnék legjobban. Msn: s(alulvonás)fecko@freemail.hu Vagy skype: s(alulvonás)fecko Köszönöm!
|
|
|
| [2080] Doom | 2007-05-29 18:39:10 |
 Legyen a két munkás A és B! A egyedül x óra alatt végzi el a munkát, míg a feladat alapján B x+12 óra alatt. Így 1 óra alatt a munka 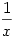 , illetve frac1x+12-ed részét végzi el. Mivel ketten együtt 8 óra alatt végeznek a teljes munkával, így , illetve frac1x+12-ed részét végzi el. Mivel ketten együtt 8 óra alatt végeznek a teljes munkával, így
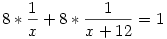
Szorozva x(x+12)-vel és nullára rendezve kapjuk, hogy
x2-4x-96=0
x1=12, x2=-8, de ez nem lehteséges.
Tehát x=12, azaz a munkát külön-külön 12, illetve 24 óra alatt végzik el.
|
| Előzmény: [2078] nervus, 2007-05-29 18:04:05 |
|
|
| [2078] nervus | 2007-05-29 18:04:05 |
 Üdv mindenkinek :) Van egy számomra nehéz matekfeladat, hálás lennék, ha valaki segítene a megoldásában. (levezetéssel leírná) "Két munkás összesen 8 óra alatt végez el egy munkát- Külön mennyi idő alatt végeznek, ha az egyik 12 órával tovább dolgozik." Előre is köszi :)
|
|
|
| [2076] Cckek | 2007-05-27 18:29:55 |
 A következő határozatlan integrált kéne kiszámolni, ha ki lehet:
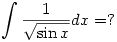
|
|
| [2075] Lóczi Lajos | 2007-05-27 16:25:45 |
 Sőt, a Newton-Leibniz-formula alapján minden olyan f folytonos függvény jó lesz, amelynek F primitív függvényére fennáll, hogy 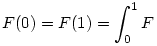 , én ebből a geometrikusabb feltételből találtam meg a , én ebből a geometrikusabb feltételből találtam meg a
f(x):=(x(x-1/2)(x-1))'=3x2-3x+1/2
példát.
|
| Előzmény: [2074] Cckek, 2007-05-27 15:44:29 |
|
|
| [2073] Lóczi Lajos | 2007-05-27 14:17:02 |
 Az eredeti f.) pont kérdésének megválaszolásához expliciten számoljuk ki az U operátor n-edik kompozícióhatványát, ami most könnyen megtehető: legyen x X rögzített elem, ekkor, ahogyan láttuk, bármely n pozitív egész esetén U[n](x)(s)=ans+bn alakú függvény, alkalmas an és bn számegyütthatókkal. Nyilván X rögzített elem, ekkor, ahogyan láttuk, bármely n pozitív egész esetén U[n](x)(s)=ans+bn alakú függvény, alkalmas an és bn számegyütthatókkal. Nyilván 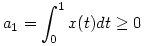 , , 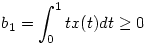 . Az U definíciójából ekkor adódik (hasonlóan ahhoz, amit már szintén láttunk az előző hozzászólásban), hogy . Az U definíciójából ekkor adódik (hasonlóan ahhoz, amit már szintén láttunk az előző hozzászólásban), hogy
an+1=an/2+bn és bn+1=an/3+bn/2.
Ennek a rekurziónak a megoldása
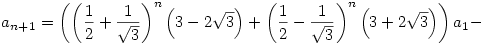
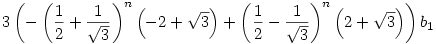
és
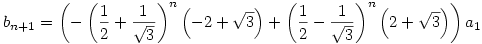
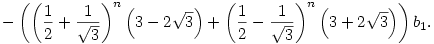
Ebből látszik, hogy tetszőleges s [0,1]-re [0,1]-re ![\lim_{n\to \infty} \root n \of {U^{[n]}(x)(s)}=1/2+1/\sqrt{3}](keplet.cgi?k=01F802F7975E68D1) , ahol az eredmény tehát egy kontans függvény [0,1]-en. , ahol az eredmény tehát egy kontans függvény [0,1]-en.
|
| Előzmény: [2072] Lóczi Lajos, 2007-05-27 13:32:17 |
|
| [2072] Lóczi Lajos | 2007-05-27 13:32:17 |
 Tudjuk, hogy a megadott X tér Banach-tér. Az U operátor nyilván lineáris.
a.) Az U operátor korlátos az X téren és ||U||op. operátornormája éppen 3/2, hiszen az X tér egységgömbjéről vett tetszőleges x függvénnyel
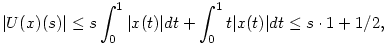
ennek a kifejezésnek a maximuma pedig s [0,1] esetén 3/2, amiből kapjuk, hogy ||U||op. [0,1] esetén 3/2, amiből kapjuk, hogy ||U||op. 3/2. Viszont az x(t) 3/2. Viszont az x(t) 1 választás mutatja, hogy ||U(x)||=3/2 elérhető. 1 választás mutatja, hogy ||U(x)||=3/2 elérhető.
b.) Mivel tetszőleges x X függvény esetén U(x) egy s X függvény esetén U(x) egy s a.s+b alakú X-beli függvény ( a.s+b alakú X-beli függvény (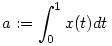 és és 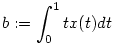 ), ezért az U operátor ranU értékkészlete részhalmaza az elsőfokú polinomok alterének X-ben, ami véges dimenziós. U tehát véges rangú, emiatt kompakt operátor. ), ezért az U operátor ranU értékkészlete részhalmaza az elsőfokú polinomok alterének X-ben, ami véges dimenziós. U tehát véges rangú, emiatt kompakt operátor.
e.) Bármely kompakt operátorra igaz, hogy spektruma csak a sajátértékeiből, illetve legfeljebb a 0 számból állhat. Mivel az X tér most végtelen dimenziós, ismert, hogy a 0 ilyenkor mindig spektrumpont. Megmutatjuk, hogy U-nak csak két nemnulla sajátértéke van.
Ehhez az U(f)= f egyenlet megoldása szükséges: keresendő az összes olyan komplex f egyenlet megoldása szükséges: keresendő az összes olyan komplex   0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely 0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely   0 számok esetén van nemtriviális megoldása az 0 számok esetén van nemtriviális megoldása az
a/3+b/2= b b
a/2+b= a a
egyenletrendszernek. Egyszerűen látszik, hogy ez csak 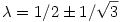 esetén van így, ezek tehát az U operátor nemnulla sajátértékei. esetén van így, ezek tehát az U operátor nemnulla sajátértékei.
U spektruma tehát 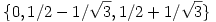 . .
c.) U nem injektív, mert a 0 egyúttal sajátérték is.
d.) A legkevésbé nyilvánvaló állítás a feladatból az, hogy a 0 szám sajátértéke is U-nak. Ehhez olyan f:[0,1] R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis 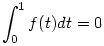 és és  . Ilyet lehet találni, de kíváncsi vagyok, ki milyen példát ad, a végén erre visszatérek. . Ilyet lehet találni, de kíváncsi vagyok, ki milyen példát ad, a végén erre visszatérek.
f.) A kérdés nem a szokásos alakú, de arra nagyon hasonlít: a kitűző véletlenül itt nem a spektrálsugárra gondolt? Az U operátor spektrálsugara nem más, mint a 0-tól legmesszebb lévő pont a kompakt spektrumból, ami jelen esetben 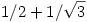 . Ismert, hogy ez a szám egyenlő a . Ismert, hogy ez a szám egyenlő a 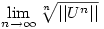 limesszel -- nem elírás az f.) pont és erre gondoltál? (Az eredeti kérdésre egy lineáris rekurzió megoldása után úgy tűnik, könnyen lehetne válaszolni, de azt még nem néztem meg.) limesszel -- nem elírás az f.) pont és erre gondoltál? (Az eredeti kérdésre egy lineáris rekurzió megoldása után úgy tűnik, könnyen lehetne válaszolni, de azt még nem néztem meg.)
g.) Jelölje Id az X tér identitásoperátorát. A válasz igen, hiszen az (U-1.Id) operátor (az X X korlátos lineáris operátorok Banach-terében) invertálható, lévén az 1 nem spektrumpont. (Sőt, emiatt több is igaz: fennáll a kezdeti feltételtől való folytonos függés is.) X korlátos lineáris operátorok Banach-terében) invertálható, lévén az 1 nem spektrumpont. (Sőt, emiatt több is igaz: fennáll a kezdeti feltételtől való folytonos függés is.)
h.) Az 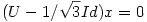 egyenletnek csak az x azonosan 0 függvény a megoldása, mert egyenletnek csak az x azonosan 0 függvény a megoldása, mert 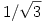 nem spektrumpont, innentől pedig l. az előbbi pontot. nem spektrumpont, innentől pedig l. az előbbi pontot.
Végül visszatérve a fent említett kérdésre, oldjuk meg az alábbi feladatot:
Adjunk példát olyan f:[0,1] R folytonos függvényre, ami nem azonosan nulla, de tetszőleges elsőfokú p polinommal R folytonos függvényre, ami nem azonosan nulla, de tetszőleges elsőfokú p polinommal 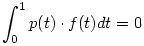 . .
|
| Előzmény: [2071] Cckek, 2007-05-16 22:22:36 |
|
| [2071] Cckek | 2007-05-16 22:22:36 |
 Legyen ![X=(C_{[0,1]},||\cdot||), ||x||=max_{t\in [0,1]}|x(t)|](keplet.cgi?k=CDF0BF029ADA9405) és és ![U:X\to X, U(x)(s)=\int_0^1{(s+t)x(t)}dt, s\in[0,1].](keplet.cgi?k=A9E0891BCE80CFA5)
Számítsuk ki illetve döntsük el a következő kijelentések igaz vagy hamis voltát:
a) ||U||=?
b) U kompakt
c) U injektiv
d) 0 sajátértéke U-nak
e) U spektruma=?
f) 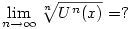
g) x-U(x)=y egyenletnek mindig van egy es csakis egy gyöke, bármely lenne y C[0,1] C[0,1]
h) A 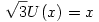 egyenletnek van 0-tól különböző gyöke egyenletnek van 0-tól különböző gyöke
|
|
|
|
| [2068] BohnerGéza | 2007-05-09 00:12:34 |
 Mutassuk meg, hogy tetszőleges n pozitív egészre van n db pithagóraszi számhármas, melyekben az átfogó (vagy az egyik befogó) megegyezik!
|
|
|
|
|
| [2064] Gubbubu | 2007-05-08 15:46:12 |
 A negyedik egyértelműen egy halászbárka, amelyet egy 200 méter magas hullám épp a csúcsára vett. A másik három vízijármű egy 200 méter oldalhosszúságú egyenlőszárú háromszög három csúcsát alkotja, melyek mindegyike 200 méter távolságra van a halászbárkától.
A "tengeralattjáró" kifogásolható megoldás, mivel nem a szó szoros értelmében a "tengeren" halad, hanem a tenger>ben< (kivéve persze, ha épp felszíni üzemmódban halad. De akkor meg nem a szó szoros értelmében vett tengeralattjáró, hanem tengeralattjáró, amelyet halászbárkának használnak).
Ez az egzakt megoldás.
|
| Előzmény: [2051] Fálesz Mihály, 2007-05-04 10:47:19 |
|
| [2063] Cckek | 2007-05-06 18:29:46 |
 324.feladat Határozzuk meg azon n-edrendű permutációk számát melyekre |p(i)-i| i i
|
|
|
|
| [2060] Lóczi Lajos | 2007-05-05 01:03:05 |
 Pár kérdés, amit nem értek:
1. Miért lenne log j=j /4 ? Szerintem nem az. /4 ? Szerintem nem az.
2. Valósban sem a kitevő, hanem az alap logaritmusát vesszük egy hatvány definíciójakor, tehát nem jó formulából indulsz ki.
3. exp(k /4) értéke nem k. /4) értéke nem k.
|
| Előzmény: [2059] jonas, 2007-05-04 22:53:31 |
|
| [2059] jonas | 2007-05-04 22:53:31 |
 Jó kérdés.
Azt ugye tudjuk, hogy log j=j /4, így azt mondhatnánk, hogy ij=exp(ilog j)=exp(ij /4, így azt mondhatnánk, hogy ij=exp(ilog j)=exp(ij /4)=exp(k /4)=exp(k /4)=k. Viszont ugyanígy mondhatnánk, hogy ij=exp(log j.i)=-k. Nem tudom, melyik a helyes, és egyáltalán azt sem, hogy értelmezve van-e a hatvány. /4)=k. Viszont ugyanígy mondhatnánk, hogy ij=exp(log j.i)=-k. Nem tudom, melyik a helyes, és egyáltalán azt sem, hogy értelmezve van-e a hatvány.
Az előző e alapú hatvány azért volt értelmezve, mert egy valós együtthatós hatványsorba bármilyen kvaternió elemet (vagy mátrixot) be tudunk helyettesíteni, hiszen egy elem hatványai felcserélhetőek egymással és a komplex számokkal is. Ezzel szemben az ix már nem valós, hanem komplex együtthatós hatványsor, amibe pedig nem helyettesíthetünk be akármilyen kvaterniót. Ha j-t az előzőhez hasonlóan egy 4x4-es valós mátrixként fogjuk fel, és behelyettesítjük a komplex hatványsorba, akkor egy nem valós komplex mátrixot kapunk, amit nem foghatunk fel kvaternióként.
|
| Előzmény: [2050] Lóczi Lajos, 2007-05-03 22:15:57 |
|
|
| [2057] Yegreg | 2007-05-04 16:24:05 |
 Igazoljuk, hogy ha x1,x2,...,xn pozitív számok, akkor 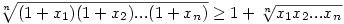 ! !
|
|
|
|
| [2054] HoA | 2007-05-04 13:48:37 |
 Attól még nem hibás egy feladat, hogy több megoldása van. Ha a kitűző azt szeretné, hogy csak egy legyen, szigorítsa a feltételeket. Tehát a 324. feladatra rímelő kitűzés: Hogyan lehet 6 gyufaszálból 4 olyan szabályos háromszöget kirakni, melyek oldala egy gyufaszál hosszú ?
|
| Előzmény: [2053] jonas, 2007-05-04 13:25:40 |
|
|
|
| [2051] Fálesz Mihály | 2007-05-04 10:47:19 |
 324. feladat. Négy hajó halad a tengeren, bármelyik kettő távolsága pontosan 200 méter. Az egyik egy motorcsónak, a második egy jacht, a harmadik vitorlás hajó. Milyen hajó a negyedik?
|
|
| [2050] Lóczi Lajos | 2007-05-03 22:15:57 |
 Akkor most már elő van készítve a terep, hogy kiszámoljuk,
323. feladat. Mennyi a kvaterniók körében ij? (Mivel nálam rosszul olvasható: "i a j-ediken".)
|
|
|
|
| [2047] jonas | 2007-05-03 15:58:36 |
 A másik lehetőség a megoldásra az, hogy a kvaterniók gyűrűjét egy mátrixgyűrűként reprezentáljuk:
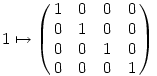
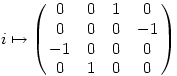
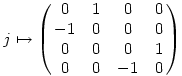
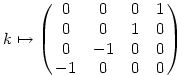
Így
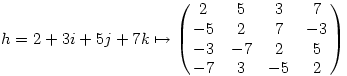
Amin pedig a szokásos módon elvégezhetjük az exponenciálást (ezt elvileg zárt képlettel is ki lehetne fejezni, mert a mátrix 4x4-es, tehát a sajátértékeket legfeljebb negyedfokú egyenlet megoldásaként kaphatjuk). Így aztán az eredmény
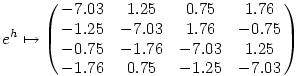
Ezt pedig csak ki kell fejezni az 1,i,j,k-nak megfelelő mátrixok kombinációjaként, és megkapjuk, hogy eh=-7.03+0.75i+1.25j+1.76k.
|
|
|
| [2045] Lóczi Lajos | 2007-05-03 00:53:09 |
 Még mindig nem egészen értem. Amikor pl. levezetjük az eix=cos (x)+isin (x) összefüggést, akkor vajon használjuk-e az i2=-1 tulajdonságot? Ha igen, akkor nem látom, hogy i helyett m-et írva ennek helyessége hogyan marad meg, ha egyszer m2 -1. -1.
|
| Előzmény: [2043] jonas, 2007-05-03 00:40:04 |
|
|
|
| [2042] Lóczi Lajos | 2007-05-02 23:19:26 |
 Két megjegyzésem van: az utolsó numerikus értékeid nincsenek összhangban az utolsó gyökös formulával.
A másik dolog fontosabb: felhasználtad az exponenciális függvény "szokásos" tulajdonságát, nevezetesen, hogy exp(a+b)=exp(a).exp(b). Ez azonban a nemkommutatív kvaterniók között általában nem áll fenn: ellenőrizhető, hogy pl. az exp(i).exp(j), exp(i+j) és exp(j).exp(i) kvaterniók mind különbözőek! Az érvelésedet ebből a szempontból tehát újra át kell vizsgálni.
|
| Előzmény: [2038] jonas, 2007-05-02 16:57:17 |
|
| [2041] Lóczi Lajos | 2007-05-02 22:54:49 |
 (Csak egy apró megjegyzés: a reziduumtételben a jobboldali szummában az összegzést nem csak a pólusokra végezzük el, hanem az összes (izolált) szinguláris helyre, ami tehát a póluson felül lehet még lényeges szingularitás is.)
|
| Előzmény: [2039] nadorp, 2007-05-02 20:29:29 |
|
|
|
|
| [2037] Lóczi Lajos | 2007-05-01 16:39:17 |
 Hm, a végeredményt tudva a bizonyítás már egyszerű.
Nyilván feltehető, hogy x0<y0, ekkor minden további tag pozitív lesz az iterációban. Könnyen igazolható, hogy létezik közös véges határérték, amit jelöljünk tehát L(x0,y0)-lal. Már részben említettem korábban, hogy L-re igazak az alábbiak: tetszőleges r>0 szám esetén
L(rx0,ry0)=rL(x0,y0), és nyilván
L(x0,y0)=L(xn,yn).
Jelölje 0<a<b esetén 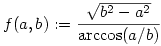 a megadott függvényt. Fel fogjuk használni, hogy a megadott függvényt. Fel fogjuk használni, hogy 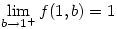 . .
Némi számolással igazolható, hogy tetszőleges r>0 és 0<a<b esetén f(ra,rb)=rf(a,b), illetve 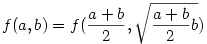 , vagyis f ugyanazokat a függvényegyenleteket teljesíti, mint L. , vagyis f ugyanazokat a függvényegyenleteket teljesíti, mint L.
Ebből azt kapjuk, hogy
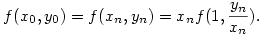
A jobb oldal n  esetén tart esetén tart 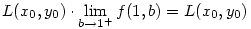 -hoz, amiből kapjuk, hogy 0 -hoz, amiből kapjuk, hogy 0 x0<y0 esetén x0<y0 esetén
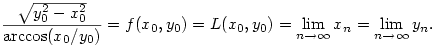
Megjegyzések, kérdések.
1. A bizonyítás kulcsa az volt, hogy képlettel megadtak számunkra egy olyan kétváltozós függvényt, amelyre igaz az 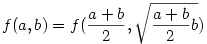 függvényegyenlet. Vajon hogyan lehet erre rájönni? (Egy differenciálegyenlet megoldásaként egyébként származtatható ez az f, csak nem látom a kapcsolatot a függvényegyenlet és a differenciálegyenlet között.) függvényegyenlet. Vajon hogyan lehet erre rájönni? (Egy differenciálegyenlet megoldásaként egyébként származtatható ez az f, csak nem látom a kapcsolatot a függvényegyenlet és a differenciálegyenlet között.)
2. A feladat ősében, a Gausstól származó számtanimértaniközép-sorozat esetében az f(a,b) függvény szerepét az
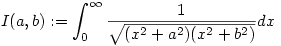
elliptikus integrál játssza. Erre az analóg 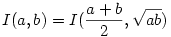 transzformációs tulajdonság igaz. Állítólag ezt az transzformációs tulajdonság igaz. Állítólag ezt az 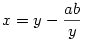 változócserével lehet belátni, de nekem nem sikerült eddig. változócserével lehet belátni, de nekem nem sikerült eddig.
322. feladat. Igazoljuk, hogy a,b>0 esetén
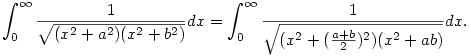
3. Mi lehet a mi feladatunkban a mögöttes integrálreprezentáció? Ez választ adhat arra a megfigyelésemre is, hogy hogyan kell kiszámolni 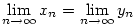 értékét akkor, ha 0 értékét akkor, ha 0 y0 y0 x0. (Tulajdonképpen a megadott f(a,b) függvény ebben az esetben is jónak tűnik, és helyes eredményt ad, csak komplex számokkal kell menet közben számolnunk.) x0. (Tulajdonképpen a megadott f(a,b) függvény ebben az esetben is jónak tűnik, és helyes eredményt ad, csak komplex számokkal kell menet közben számolnunk.)
|
| Előzmény: [2036] Cckek, 2007-05-01 14:16:56 |
|
|
| [2035] Lóczi Lajos | 2007-04-30 01:31:36 |
 Vagy kicsit rendezettebb formában:
jelölje L(x0,y0) a sorozatok közös limeszét a kezdőérték függvényében. Mivel pozitív r>0 esetén fennáll az
L(rx0,ry0)=rL(x0,y0)
skálázási tulajdonság, elég csak az L(1,y0) alakú értékekkel foglalkoznunk, ahol y0>1. Így
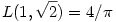
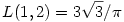
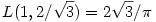 , ,
illetve a két kilógó érték, amit megtaláltam:
L(0,1)=2/ , és a meglepő , és a meglepő 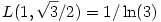 (ami nincs a feladatban, mivel itt x0>y0). (ami nincs a feladatban, mivel itt x0>y0).
Nos ezekre kellene keresni valami szép integrálformulát...
|
| Előzmény: [2034] Lóczi Lajos, 2007-04-30 00:51:38 |
|
| [2034] Lóczi Lajos | 2007-04-30 00:51:38 |
 Némi kísérletezéssel az alábbiakat kaptam:
Ha (x0,y0)=(0,y0), akkor a közös limesz 2y0/ . .
Ha (x0,y0)=(1,2), akkor a közös limesz 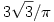 . .
Ha 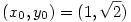 , akkor a közös limesz 4/ , akkor a közös limesz 4/ . .
Sajnos ebből még nem tudom megsejteni a limeszfüggvény formáját a kezdőértékek függvényében, de könnyen elképzelhető, hogy a számtanimértaniközép-sorozathoz hasonló elliptikus integrál áll a háttérben, és akkor reménytelen lenne a tippelgetés...
|
| Előzmény: [2027] Cckek, 2007-04-28 11:36:13 |
|
|




 /4 speciális esetben adódó
/4 speciális esetben adódó 

 Q?
Q?  (sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon.
(sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon. 
 (3) irracionális" állításról is szól.
(3) irracionális" állításról is szól.
 bn jelölje az asszimptotikus egyenlőséget, tehát hogy
bn jelölje az asszimptotikus egyenlőséget, tehát hogy 
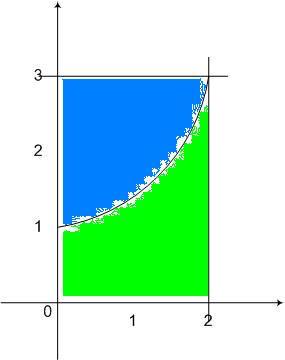
 [c,d] folytonos, növekvő, bijektív függvény akkor
[c,d] folytonos, növekvő, bijektív függvény akkor  [a+
[a+ ,b+
,b+ zn+zn-1+1=0, a két egyenletet kivonva egymásból kapjuk zn-1-z=0 tehat zn-2=1. De 0=zn+z+1=zn-2.z2+z+1=z2+z+1 tehát z harmadrendű egységgyök, tehát zn-2=z3k=1
zn+zn-1+1=0, a két egyenletet kivonva egymásból kapjuk zn-1-z=0 tehat zn-2=1. De 0=zn+z+1=zn-2.z2+z+1=z2+z+1 tehát z harmadrendű egységgyök, tehát zn-2=z3k=1 2
2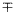 2
2
 1,2=2
1,2=2





 n , x2=-
n , x2=- Dfk+1, k
Dfk+1, k 0.Mivel G csoport,(g
0.Mivel G csoport,(g 0 igy izomorf Z vel.
0 igy izomorf Z vel.  ,x+
,x+ n
n
 ) folytonos függvényeket melyekre:
) folytonos függvényeket melyekre: 
 1 triviális becslést alkalmazva
1 triviális becslést alkalmazva  n úgy van definiálva, hogy
n úgy van definiálva, hogy 


 3/2. Viszont az x(t)
3/2. Viszont az x(t) 1 választás mutatja, hogy ||U(x)||=3/2 elérhető.
1 választás mutatja, hogy ||U(x)||=3/2 elérhető.  a.s+b alakú X-beli függvény (
a.s+b alakú X-beli függvény (