| [2633] Róbert Gida | 2008-04-28 19:11:45 |
 Találjuk meg a két legkisebb pozitív egész 1-nél nagyobb páratlan N számot, melyre teljesül, hogy: minden lnko(a,N)=1 esetén 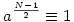 mod N teljesül! Mi a sejtésünk: végtelen vagy véges sok ilyen N szám van? mod N teljesül! Mi a sejtésünk: végtelen vagy véges sok ilyen N szám van?
|
|
|
| [2631] Róbert Gida | 2008-04-27 00:52:00 |
 Egy megoldás rá: Legyen s=a1+an rögzített, ekkor, ha s fix, akkor a jobb oldal is fix. De mi lesz a bal oldal maximuma (rögzített s esetén)? Legyen x=a2...ak és y=an-k+1...an-2, a bal oldalon elég az első és utolsó tagot nézni:
max(a1*x+y*an)=max(x,y)*s, ha s=a1+an, és a maximum felvétetik olyan helyen (is), ahol a1=0 vagy an=0, ezt beírva az eredeti feladatot kapjuk meg csak n tag helyett (n-1) taggal. Azaz leszállhatunk, egészen n=k-ig, ami a triviális eset, hiszen ez éppen a számtani-mértani egyenlőtlenség.
Egyenlőség viszont sokféleképpen lehet, például k=1-nél mindig egyenlőség van. n=3,k=2-nél pontosan akkor, ha a1-a2+a3=0
|
| Előzmény: [2630] Gyöngyő, 2008-04-26 22:06:26 |
|
| [2630] Gyöngyő | 2008-04-26 22:06:26 |
 Szisztok!
Legyen k és n pozitiv egészek és k=<n, és legyen a1,a2,...an nemnegativ valós számok. Bizonyítsuk be,hogy
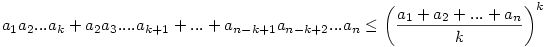
|
|
| [2629] Ratkó Éva | 2008-04-21 13:16:07 |
 Kedves CD iránt érdeklő és tájékozott fórumozók! Az, hogy a KöMaL eltűnt a sulinet honlapról, sajnos nem a mi hatáskörünk: higgyétek el, mi is azt szeretnénk, ha még mindig ott lenne. Volt velük egy ötéves szerződésünk, melyet a lejárta után nem óhajtottak megújítani, és jelenleg is ez az állapot áll fenn. Valóban, szkennelt formában elérhetőek a számok a mi honlapunkon, teljesen ingyen. (Itt egy másik oldal is, ahol elérhetők, méghozzá oldalanként: db.komal.hu/scan ) Ahhoz, hogy a) vagy egy hasonlóan működő honlapot gyártsunk b) a CD-t frissítsük vagy internetes vagy új CD-kiadás formájában, egy jó programra és ehhez pénzre van szükségünk. A HEFOP pályázat arról szólt, hogy adatokkal feltöltjük az adatbázisunkat.
Egyébként a pályázatnak 2006 decemberében vége volt, azóta még nem kaptuk meg az általunk kifizetett pénz 20%-át. Tehát adott egy egész szépen feltöltött adatbázis, amivel még 2 teendő van - ez folyik most- : 1.) a szöveghez az ábrákat bevinni - ezt elkezdték, de nem fejezték be - 2.) ellenőrizni kell, hogy tényleg jók-e a bevitt szövegek - ugyanis az adatbevitelkor sok hiba keletkezhetett.
Valóban eladtunk kb. 500 Cd-t, ebből számoljátok ki hány ember fizetése (minimálbér) finanszírozható!? Hány hónapig? (persze a CD nyomása és elkészítése és az azt működtető valóban nem egészen felhasználóbarát program megíratása sem volt ingyen - amúgy épp ezért szándékoznánk valami mai igényeknek megfelelőbb feldolgozást) Szóval elnézést, de ma csak itt tartunk. Egyébként teljesen igazatok van, már rég működnie kéne ennek az archívumnak valamilyen formában. A jó hír az, hogy legalább a KöMaL kiadására és a KöMal-honlap és FÓRUM működtetésére épp hogy futja a MATFUND (és az adófizetők) pénzéből :-)
Oláh Vera
|
| Előzmény: [2626] Cogito, 2008-04-13 14:11:36 |
|
| [2628] sakkmath | 2008-04-13 16:17:36 |
 Szia Gyöngyő!
Úgy tűnik, az első öt jól felírt sorozattag után a sok szám és vessző között eltévedtél, s talán ezzel magyarázható, hogy több hibával írtad fel a sorozat hátralévő tagjait. Megpróbálom hiba nélkül leírni a sorozat első 11 tagját, remélem, sikerül: 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, 31131211131221, 13211311123113112211, 11131221133112132113212221, ...
Végül nézzük a rekurziós képzési szabályt; hogyan kapjuk a 11. tagot a tizedikből: 1db 1, 1db 3, 1db 2, 2db 1, 1db 3, 3db 1, 1db 2, 1db 3, 2db 1, 1db 3, 2db 1, 2db 2, 2db 1.
Üdv: sakkmath
|
| Előzmény: [2627] Gyöngyő, 2008-04-13 14:36:32 |
|
| [2627] Gyöngyő | 2008-04-13 14:36:32 |
 Sziasztok!
Van egy jópofa feladatom!
folytasd:
1,11,21,1211,111221,31,2211,13112221,1113213211,31131211321, 132113111231131211....
üdv: Zsolt
|
|
| [2626] Cogito | 2008-04-13 14:11:36 |
 A KöMaL-szerkesztőség erről csak ennyit ír. E szűkszavú híren kívül illett volna azt is közölni, hogy a mostani állapot mégis meddig tart, illett volna megindokolni a "nem elérhető"-ség okát, s végül, de nem utolsó sorban, illett volna elnézést is kérni a legalább másfél éve tartó, bosszantó helyzetért.
Szerencsére van egy lehetőség, hogy saját cd-t készítsünk a KöMaL első 100 évének archívumáról. A hogyanhoz klikk ide. (Egy 523 MB-os ZIP-állományt kell/lehet letölteni...)
Az utóbbi linken a 2005 nyarán megjelent "Irány a Nobel-díj KöMaL 1994-2003" című CD-ről többek között ez olvasható: " ... minden vásárlót regisztrálunk, és számukra a jövőben lehetővé tesszük, hogy a folyamatosan bővülő tartalmat a meglevő CD-jük frissítéseként letölthetik erről a web-címről ...". A közlemény így zárul: "Az összes megjelent füzet digitalizálása körülbelül 3 évet vesz majd igénybe."
Ezek alapján joggal kérdezhetik a regisztrált felhasználók, hogy:
1) Az eltelt csaknem 3 év alatt miért nem lehetett semmiféle frissítést letölteni?
2) Az óvatos "körülbelül 3 év" hány év lesz a valóságban?
|
| Előzmény: [2625] kdano, 2008-04-11 19:47:08 |
|
|
|
|
| [2622] Lóczi Lajos | 2008-03-23 22:25:16 |
 Elegáns. Egy másik megközelítés lehet, ha a Róbert Gida által felvázolt módon expliciten kiszámoljuk a szóban forgó 5 darab, közönséges 3-dimenziós tetraéder térfogatnégyzetét: ez nagyon egyszerű pl. (a Héron-képletet is általánosító) Cayley-Menger determinánsok segítségével.
|
| Előzmény: [2621] Káli gúla, 2008-03-23 21:16:30 |
|
|
|
| [2619] Káli gúla | 2008-03-23 20:41:18 |
  -vel egy kiválasztott koordinátatengelyre merőleges hipersíknak és a szimplex origóval szemközti lapsíkjának a szögét gondoltam jelölni. -vel egy kiválasztott koordinátatengelyre merőleges hipersíknak és a szimplex origóval szemközti lapsíkjának a szögét gondoltam jelölni.
Az elsőfokú közelítés s az ennek megfelelő sáv egy korábbi példádhoz kapcsolódott (2608. ill. 2610. (A d szélességű "egyenes sáv" azon pontok mértani helye a síkban, melyeknek egy adott egyenestől mért távolsága legfeljebb d/2 :)
|
| Előzmény: [2617] Lóczi Lajos, 2008-03-23 20:06:20 |
|
|
| [2617] Lóczi Lajos | 2008-03-23 20:06:20 |
 De mit jelent itt a  szög? És mit az "elsőfokú közelítés"? Sajnos nem értem, mit mond a térfogatokra nézve az, ha az "egyenes sáv" szélessége legalább 1. Kérlek, adj még magyarázatot :) szög? És mit az "elsőfokú közelítés"? Sajnos nem értem, mit mond a térfogatokra nézve az, ha az "egyenes sáv" szélessége legalább 1. Kérlek, adj még magyarázatot :)
|
| Előzmény: [2616] Káli gúla, 2008-03-23 17:59:33 |
|
| [2616] Káli gúla | 2008-03-23 17:59:33 |
 A "ferde" lap mértéke merőleges vetítésnél akárhány dimenzióban is cos  -vel szorzódik, lényegében pontosan azért, mert a ferde lap normálvektorának megfelelő koordinátája cos -vel szorzódik, lényegében pontosan azért, mert a ferde lap normálvektorának megfelelő koordinátája cos  . .
Az elsőfokú közelítésre visszatérve, egy d széles sávban akárhogyan veszünk három A, B, C pontot, az ABC háromszög valamelyik magasságának hossza legfeljebb d lehet. Bizonyítás. Húzzunk a három ponton keresztül a sáv tengelyére merőlegesen három egyenest, és legyen pl. a B-n átmenő a középső. Ekkor az AC szakasznak van közös pontja (B1) a középső egyenessel, így mb BB1 BB1 d. d.
A -1, 0 és 1 pontokhoz tartozó parabolapontok egy 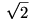 befogójú egyenlőszárú derékszögű háromszöget alkotnak. Ebben a háromszögben a legkisebb magasság 1, így egy ezt tartalmazó egyenes sáv szélessége is legalább 1. befogójú egyenlőszárú derékszögű háromszöget alkotnak. Ebben a háromszögben a legkisebb magasság 1, így egy ezt tartalmazó egyenes sáv szélessége is legalább 1.
|
| Előzmény: [2615] Lóczi Lajos, 2008-03-23 00:56:14 |
|
| [2615] Lóczi Lajos | 2008-03-23 00:56:14 |
 Oldjuk meg a feladatot 4 dimenzióban is.
Tekintsük a (0,0,0,0) origót és az (a,0,0,0), (0,b,0,0), (0,0,c,0), (0,0,0,d) pontokat (ahol a,b,c,d>0). Ennek az 5 pontnak a konvex burka meghatároz egy négydimenziós testet, melynek 5 db háromdimenziós "oldallapja" van.
Mi a kapcsolat ezen 5 lap térfogata között?
|
| Előzmény: [2613] Lóczi Lajos, 2008-03-20 22:41:55 |
|
|
| [2613] Lóczi Lajos | 2008-03-20 22:41:55 |
 Tekintsünk egy olyan tetraédert az első térnyolcadban, amelynek egyik csúcsa az origó, a többi három csúcs pedig a három koordinátatengely egy-egy pozitív pontja. Mi a kapcsolat e tetraéder oldallapjainak területe között?
|
|
| [2612] rizsesz | 2008-03-18 23:17:06 |
 Szóval tisztázom a saját irományomat, immáron TeXben.
Tehát ez a függvény nem más, mint x2 eltolva egyaránt az x és az y tengelyen, de hála a szabad paraméterezésnek, gondolkodhatunk csak az x2 világában.
A feladat azt kéri, hogy ennek a függvénynek egy (x0;x0+2) szakaszán a függvény abszolútértékének maximuma minimális legyen. Tegyük fel, hogy x0 már a növekvő szakasz része. Ekkor, mint az könnyen ellenőrizhető, a felvett fv.-értékek különbsége legalább 4 lesz (a sima x2-nél x0 minimuma 0, a különbség pedig 4x0+4, ami legalább 4). A skatulya-elv miatt ennek a legalább 4 értékű növekedésnek legalább 2 hosszú része vagy negatív, vagy pozitív, de legalább 2; így a maximum is legalább 2 az abszolútérték miatt. Ugyanez elmondható a monoton csökkenő részre is, marad a közbülső rész, amikor a másodfokú áthalad a minimumhelyén. Tfh. (x0;x0+2) tartalmazza a minimumhelyet, ami most a szimmetria miatt legyen 0. Ekkor x0 negatív. Teljesen az előző logikát követve x0 és x0+2 négyzeteik közül a nagyobb minimumát keressük. Ez már könnyebb feladat, a két parabola metszéspontja adja ki, az x0=-1 helyen, a föggvényérték 1, ekkor valóban kijön, hogy legalább 1/2 a minimum, ami a logikát követve el is érhető.
|
| Előzmény: [2608] Lóczi Lajos, 2008-03-18 01:49:58 |
|
| [2611] rizsesz | 2008-03-18 19:05:00 |
 A közölt függvény lényegében a sima másodfokú x négyzet. Ezt tologatjuk. Ennek nézzük 2 hosszú szakaszait. Ha már a teljes szakasz a növekvő részen van, akkor legalább 4 lesz az y értékek különbsége. Ez egyúttal azt jelenti, hogy az legalább 2 hosszú lesz a negatív vagy a pozitív rész, tehát lesz olyan y, aminek az abszolútértéke legalább 2 a monotonitás miatt. Ugyanez igaz a csökkenő részre. Amikor áthalad az minimumhelyén, akkor a legkisebb érték az ehhez tartozó, a legnagyobb pedig ynégyzet és (2-y)négyzet maximuma. itt y a baloldalra haladás a minimumhelytől. y>1 esetén ez a 1., ellenkező esetben a 2. mivel y értéke. könnyen látható, hogy ez akkor lesz minimális, ha y=1, ekkor 1 lesz a minimum és a maximum különbsége, tehát legalább 1/2 a keresett megoldás, ami így ki is jön. elnézést a TeXtelenségért.
|
| Előzmény: [2610] Lóczi Lajos, 2008-03-18 16:05:37 |
|
|
|
|
| [2607] S.Ákos | 2008-03-17 19:35:36 |
 Valóban hülyeség, nem fogalmaztam elég pontosan. amilyen függvénygörbét láttam, az alapján ezt tudtam mondani, legközelebb nem teszem. A növekedést pedig nem úgy értettem, hogy ha n<m akkor f(n)<f(m), hanem valamilyen érték körül ugrál.
|
| Előzmény: [2603] Róbert Gida, 2008-03-16 14:31:49 |
|
|
| [2605] rizsesz | 2008-03-16 18:41:35 |
 Róbert Gida, én téged baromira nem értelek. Miért kell kérkedned a tudásoddal? Látszik, hogy értelmes, matematikából nagyon tehetséges ember vagy, de ahogy megnyilvánulsz néha ezen a fórumon, az igazán nem egy értelmes emberhez méltó.
|
| Előzmény: [2603] Róbert Gida, 2008-03-16 14:31:49 |
|
|
|
|
| [2601] Róbert Gida | 2008-03-16 14:04:28 |
 Triviális. Legyen m=1236789689135*n-206131614856 alakú prím, ismeretes, hogy ezekből végtelen sok van Dirichlet tétele miatt (feltétele teljesül), ilyen prímekre  (6*m)< (6*m)< (6*m+1) lesz, hiszen az elsőt pontosan ki tudod számolni, mert m az prím, a másodikat pedig becsüld alulról, használva azt, hogy ekkor 6*m+1 osztható minden prímmel 5-től 37-ig, így *találtam ki*. Például n=25-re prímet ad, azaz m=30713610613519 megoldás lesz, ezt közvetlenül is ellenőrizheted, ez persze nem biztos, hogy a legkisebb megoldás, hiszen egy más konstrukció is adhat jó m-et. (6*m+1) lesz, hiszen az elsőt pontosan ki tudod számolni, mert m az prím, a másodikat pedig becsüld alulról, használva azt, hogy ekkor 6*m+1 osztható minden prímmel 5-től 37-ig, így *találtam ki*. Például n=25-re prímet ad, azaz m=30713610613519 megoldás lesz, ezt közvetlenül is ellenőrizheted, ez persze nem biztos, hogy a legkisebb megoldás, hiszen egy más konstrukció is adhat jó m-et.
|
| Előzmény: [2599] Gyöngyő, 2008-03-16 13:00:58 |
|
| [2600] S.Ákos | 2008-03-16 13:58:06 |
 Megnézve az [1;1020] intervallumot, eddig nem találtam megoldást, és úgy néz ki, hogy a függvényértékek közötti eltérés nő, egyre nagyobb lesz 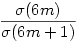 . Többet sajnos még nem tudok mondani. . Többet sajnos még nem tudok mondani.
|
| Előzmény: [2599] Gyöngyő, 2008-03-16 13:00:58 |
|
| [2599] Gyöngyő | 2008-03-16 13:00:58 |
 Sziasztok!
Tudnátok segíteni a következő feladatban:
Keressük a legkisebb pozitiv egész m-et amelyre  (6m)< (6m)< (6m+1)fenntáll. (6m+1)fenntáll.
A másik kérdés pedig,az h mutassuk meg,hogy a fennti egyenlőtlenségnek végtelen sok megoldása van.
Ahol  (m) az osztók összegét jelenti. (m) az osztók összegét jelenti.
Köszönettel
|
|
| [2598] szbela | 2008-03-15 15:13:01 |
 Sziasztok!
Esetleg megnézzük (i) x=0, (ii) x=0 és y=0 esetekre? Bár nem tudom, hogy ez így jó-e.
(i) x=0 : f(x+f(y))=f(0+f(y))=f(f(0))+f(y)
(ii) x=0 és y=0 : f(x+f(y))=f(0+f(0))=f(f(0))=f(f(0))+f(0)
(i)-nek és (ii)-nek teljesülnie kell: (ii)-ből következett, hogy f(f(0))=f(f(0))+f(0), ebből f(0)=0 tehát f(f(0))=0 szintén. Ezt (i)-be helyettesítjük és kapjuk, hogy f(f(y))=f(y) Ennek persze minden y-ra teljesülnie kell. És mivel f: R->R -be képez, ezért ha f(y)=a, akkor f(a)=a f(y)=f(f(y)) miatt. f tehát az identitásfüggvény lenne.
|
| Előzmény: [2595] Gyöngyő, 2008-03-14 20:29:51 |
|
| [2597] Cckek | 2008-03-15 09:56:31 |
 Egy ötlet: f(f(x+f(y)))=f(f2(x)+f(y))=f(f(y)+f2(x))=f(f(f(y)))+f2(x)=f2(f(y))+f2(x). Legyen f(y)=t Imf Imf
Ekkor f2(x+t)=f2(x)+f2(t), tehát az f2 függvény kielégíti Cauchy funkcionálegyenletét az RxImf halmazon.
|
| Előzmény: [2595] Gyöngyő, 2008-03-14 20:29:51 |
|
|
| [2595] Gyöngyő | 2008-03-14 20:29:51 |
 Sziasztok!
Nekem is van egy érdekes feladatom:
Keressük meg az összes R-ből R-be képző nemcsökkenő függvényt amelyre f(x+f(y))=f(f(x))+f(y) fennáll minden valós x és y-ra
|
|
| [2594] kicsipega | 2008-03-10 09:44:52 |
 sziasztok!
Még új vagyok negyon tetszik ez a fórum, bár még nem olvastam égig az összes feladatot és megoldást. A 44. feladatnak van egy kicsit nehezítet változa. A fekete és fehér marhák egy négyzetbe, a tarka és barna marhák egy háromszögbe tudnak felsorakozni.
Ha már volt bocsi az ismétlésért.
Gabi
|
|
|
| [2592] epsilon | 2008-03-09 21:16:09 |
 Ha elvégzed az 1/x=y változócserét, akkor visszakapod a [2589] Cckek integrálját aminek az eredménye éppen [2590] Lóczi Lajos-tól. Nem de?
|
|
|
|
|
| [2588] Róbert Gida | 2008-01-28 00:29:29 |
 Aszimptotikusan 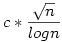 , ahol c>0 konstans, ez is megsejtehő, mint például az ikerprím konstans. , ahol c>0 konstans, ez is megsejtehő, mint például az ikerprím konstans.
Freud Gyarmati régi ELTE számelmélet jegyzetét megnéztem, ott sincs kimondva a sejtés, csak az irreducibilitás és a primitívség, de ez nem elég! n2+n+2 polinom például irred. és primitív, de csak a 2-t veszi fel prímként (minden egész helyen a polinom értéke páros). Szerintem már csak annyit kell feltenni, hogy, ha a polniom foka d, akkor minden p d-re a polinom Fp[x]-ben nem az azonosan nulla polinom. (p>d-re, ha a polinom primitív, akkor a fokszámtétel miatt nem lehet nulla a polinom). Ez persze a te n2+n+1 polinomodat nem érinti, ez is teljesül rá. d-re a polinom Fp[x]-ben nem az azonosan nulla polinom. (p>d-re, ha a polinom primitív, akkor a fokszámtétel miatt nem lehet nulla a polinom). Ez persze a te n2+n+1 polinomodat nem érinti, ez is teljesül rá.
|
| Előzmény: [2587] V Laci, 2008-01-27 22:28:12 |
|
|
| [2586] Róbert Gida | 2008-01-27 19:53:47 |
 Tehát, hogy végtelen sok van-e, az a kérdés? p=2 nem megoldás, egyébként feltehető, hogy p páratlan prím, így a négyzetszám is páratlan, legyen ez (2*n+1)2, ekkor rendezve az kell, hogy p=n2+n+1 alakú prímből végtelen sok legyen, mivel ez irreducibilis és primitív polinom, ezért egy idevonatkozó mély sejtés szerint végtelen sok ilyen prím van (elsőfokúra Dirichlet tétel, nagyobbra nem tudjuk, hogy igaz-e). Sőt ha a számukat kérdezed adott N-ig, hogy hány ilyen p prím van az is megsejthető.
|
| Előzmény: [2585] V Laci, 2008-01-27 19:22:26 |
|
| [2585] V Laci | 2008-01-27 19:22:26 |
 Sziasztok!
Nemrég találkoztam az alábbi érdekes problémával (bár lehet, hogy nehezebb, mint érdekesebb).
Hány olyan p prím van, amelyre 4p-3 négyzetszám?
|
|
|
| [2583] komalboy | 2008-01-26 13:36:58 |
 h lehet azt igazolni, h a két rekurzió ugyanaz?
|
|
|
|
|
|
|
|
|
| [2575] komalboy | 2008-01-24 18:19:19 |
 Bizonyítsuk be, h a sorozat tagjai egészek:
|
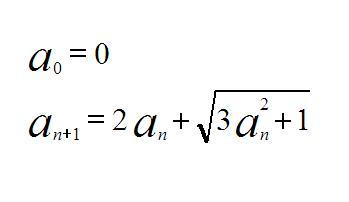 |
|
|
| [2573] Lóczi Lajos | 2008-01-24 01:48:39 |
 Igaz-e, hogy ha a,b,c tetszőleges pozitív valós számok, de a b, akkor b, akkor
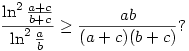
|
|
| [2572] epsilon | 2008-01-22 17:37:56 |
 Kedves Lóczi Lajos! Alaposan átnéztem a [2564]-es hozzászólásnál a megoldásodat, és úgy látom, hogy ennél elemibbet nem lehet találni, de ez amit a fogó tétellel meg a L'Hospital szabállyal függvényhatárértékből származtattál, feldolgozható a tehetségesebb, pontosabban kiváltságosn jó 12-ik osztályos tanulókkal, ellenben teljesen igazatok van, osztozom a feladatról írt véleményetekben, hogy 12. osztályban ha csak nem idomítottak be valakit ilyen trükkökre, elég nehezen jön rá ilyen megoldásra. Ismételten kösz mindkettőtöknek, nadorpnak is, hogy rávilágítottatok a feladat gyökerére is! Üdv: epsilon
|
|
|
| [2570] epsilon | 2008-01-22 06:39:13 |
 Kedves nadorp és Lajos! Köszi mindkettőtöknek a valóságos szép leckét. Én az asszimptótikus megközelítést elméletileg a Taylor-féle sorbafejtéssel képzelném el kikerülni, mondjuk a Lagrange Tételnél 1 lépéssel kellene továbbhaladni, a 2-ik rendü deriváltig az 1-ik helyett, de ez csak elképzelésem, tüzetesen átnézem amit írtatok, és ...hátha lehetne? Mégegyszer kösz Mindkettőtöknek! Üdv: epsilon
|
| Előzmény: [2568] nadorp, 2008-01-21 22:07:38 |
|
| [2569] Csimby | 2008-01-21 23:00:40 |
 Hasonlóan, mint Káli gúlának, szóval nincs benne új ötlet, csak nem tudtam továbbmenni. Azért beírom: T.f.h. ab rac., ekkor (a2+b2)(a5+b5)=a7+b7+a2b2(a3+b3) is rac., amiből köv. a2+b2 is rac. Másrészt 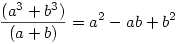 irracionalitása miatt a2-ab+b2 irrac., tehát a2+b2 irrac. Villám. irracionalitása miatt a2-ab+b2 irrac., tehát a2+b2 irrac. Villám.
|
| Előzmény: [2566] Lóczi Lajos, 2008-01-21 19:38:20 |
|
| [2568] nadorp | 2008-01-21 22:07:38 |
 Kedves Epsilon !
Nem tudom, hogy lehetne kikerülni az asszimptotikus egyenlőséget, de talán ez megfelelő lesz:
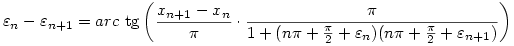
Ha most felhasználjuk, hogy az "arc tg"-ben az első tört 1-be tart, a második nevezőjének a nagyságrendje  2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés". 2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés".
|
| Előzmény: [2563] epsilon, 2008-01-21 17:16:39 |
|
| [2567] nadorp | 2008-01-21 21:45:23 |
 Lajos megoldása rövidebb, de álljon itt az enyém is.( Ha túl hosszú és unalmas, akkor hagyjátok ki.)
Azt láttuk, hogy
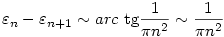
Tehát tetszőlesges  >0-hoz létezik N, ha n>N, akkor >0-hoz létezik N, ha n>N, akkor
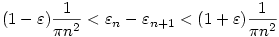
Ezt elvégezve az n+1,...,n+k-1 számokra is és összeadva a k db egyenlőtlenséget
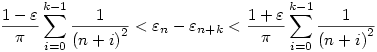
Ha most felhasználjuk,hogy
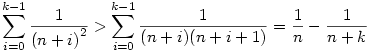 és hogy és hogy
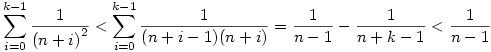 akkor akkor
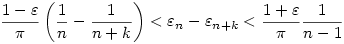 teljesül minden k-ra.Ha k=n2 teljesül minden k-ra.Ha k=n2
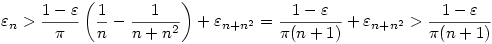 Másrészt Másrészt
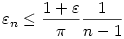 is igaz, ui. ellenkező esetben is igaz, ui. ellenkező esetben
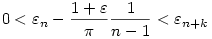 igaz lenne minden k-ra, de ez ellentmond a 0-ba tartásnak. Tehát igaz lenne minden k-ra, de ez ellentmond a 0-ba tartásnak. Tehát
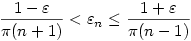
|
| Előzmény: [2563] epsilon, 2008-01-21 17:16:39 |
|
|
| [2565] Lóczi Lajos | 2008-01-21 19:36:40 |
 Ez tehát azt mutatja, hogy a fixpontegyenlet gyökei aszimptotikusan
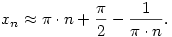
Kíváncsiságból egy lépéssel tovább is kiszámoltam, az előzőhöz hasonló érveléssel (a nehézség nem nőtt), és azt kaptam, hogy

|
| Előzmény: [2564] Lóczi Lajos, 2008-01-21 19:29:01 |
|
| [2564] Lóczi Lajos | 2008-01-21 19:29:01 |
 Tényleg nem értem, hogy lehetne ez egy tesztkérdésben benne (amikor, ahogyan illusztráltam, sok 18 évesnek problémája van a törtekkel és hatványozás azonosságaival...)
Szóval technikailag kicsit talán egyszerűbb így elmondani:
xn=n + + /2- /2- n, ebből egyszerűen kapjuk (figyelembe véve, hogy xn melyik intervallumban van, illetve hogy xn melyik egyenlet megoldása), hogy n, ebből egyszerűen kapjuk (figyelembe véve, hogy xn melyik intervallumban van, illetve hogy xn melyik egyenlet megoldása), hogy
 /2-arctg(n /2-arctg(n + + /2- /2- n)= n)= n. n.
Most használjuk fel, hogy 0< n< n< /2 (de konkrét becslés nem is kell, elegendő annyit tudnunk, hogy /2 (de konkrét becslés nem is kell, elegendő annyit tudnunk, hogy  n korlátos, hiszen nullsorozat). Ekkor n korlátos, hiszen nullsorozat). Ekkor  /2-arctg(n /2-arctg(n + + /2- /2- n) alulról és felülről becsülhető n) alulról és felülről becsülhető  /2-arctg(n /2-arctg(n +konstans) alakú kifejezésekkel, használva az arkusz tangens monotonitását. Ezt most már valós x-ekre kiterjesztve, a L'Hospital-szabállyal egy deriválás után látszik, hogy +konstans) alakú kifejezésekkel, használva az arkusz tangens monotonitását. Ezt most már valós x-ekre kiterjesztve, a L'Hospital-szabállyal egy deriválás után látszik, hogy
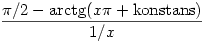
limesze (x tart végtelen esetén, tetszőleges, rögzített "konstanssal") 1/ , a közrefogási elv miatt az előző bekezdés értelmében tehát n , a közrefogási elv miatt az előző bekezdés értelmében tehát n n határértéke valóban 1/ n határértéke valóban 1/ . .
|
| Előzmény: [2563] epsilon, 2008-01-21 17:16:39 |
|
| [2563] epsilon | 2008-01-21 17:16:39 |
 Helló nadorp! A feleletválasztós tesztben ahonnan a feladat származik lehetséges válaszok: 1, 0, 1/pi, pi/2, pi/4 és ahogy nézem, az asszimptótikus megközelítéseid alapján 1/pi lenne...csak az a gondom, hogy nem igazán látom az utolsó 2 sorodban honnan vannak az asszimptótikus megközelítések, na meg hogyan lehetne ezt a feladatot 12. osztályt végzettnek feladni (mert az kapta fel) hiszen az asszimptótikus megközelítés nincs a tananyagban...szóval vajon hogyan lehetne a megoldást leszállítani 12. osztályos szintre? Üdv: epsilon
|
|
|
|
|
|
| [2558] epsilon | 2008-01-21 13:15:55 |
 Kedves Lajos! Amint nézem, Te éppen a kijavított feladatra is céloztál, éppen az érdekelne, hogyan lehetne megkapni egy olyan asszimtótikus sorbafejtést, vagy esetleg egy olyan dupla egyenlőtlenséget, amiből a limesz kiszámítható lenne, mert azt nem tudom "megfogni", hogy x(n) a tgx=x megoldása, az illető intervallumban. Üdv: epsilon
|
| Előzmény: [2554] Lóczi Lajos, 2008-01-20 22:33:56 |
|
| [2557] epsilon | 2008-01-21 07:01:13 |
 Köszi jonas, sajnos este volt, és megint elnéztem valamit(a limesz alatti x helyett persze n van), a kiszámítandó limesz előtt van egy n (ezért is mondottam nehéznek, és természetesen, hogy a zárójel határártéke nulla kell legyen, hiszen határozatlan eset az érdeke). Elnézést mindenkitől a figyelmetlenségemért, és továbbra is várom a segítségeteket, üdv: espilon
|
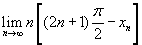 |
| Előzmény: [2553] jonas, 2008-01-20 21:08:15 |
|
|
| [2555] Csimby | 2008-01-20 23:06:19 |
 Szia! Tetszik a feladatod. Sajnos nem tudtam még megoldani, pedig nagyon kíváncsi vagyok. Annyi jött ki, hogy a,b,ab nem lehet racionális. Amúgy saját feladat, vagy honnan van? Ha tudod a megoldást megosztod velem? Csak mert tanulnom kéne de ez elvonja a figyelmemet :-) (ha nem akarod a fórumon lelőni, akkor a csimbyfree@freemail.hu címre is küldheted) Köszi! Csimby
|
| Előzmény: [2548] MateMSR, 2008-01-19 22:29:14 |
|
| [2554] Lóczi Lajos | 2008-01-20 22:33:56 |
 Vagyis 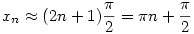 . Pontosabban, azt láttuk, hogy ha . Pontosabban, azt láttuk, hogy ha
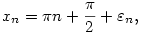
akkor  n a nullához tart. n a nullához tart.
Ezt persze lehet folytatni (a végtelenségig): mi lesz xn aszimptotikus sorfejtésének következő tagja, azaz mennyi

(ha egyáltalán létezik)?
|
| Előzmény: [2553] jonas, 2008-01-20 21:08:15 |
|
|
|
| [2551] epsilon | 2008-01-20 20:42:43 |
 Tisztelt Kollégák! Nem tudom, hogy ez a feladat inkább nehezebb mint érdekesebb, vagy érdekesebb mint nehezebb ( a hosszabb-zöldebb krokodil meséje), ezért ide tettem, de a lényeg, nem találok kiindulópontot a megoldásához, távközlési egyetemre való tesztvizsgán láttam. Ha Valakinek van valami jó ötlete, előre is köszönöm! Üdv: epsilon
|
 |
|
|
|
| [2548] MateMSR | 2008-01-19 22:29:14 |
 Sziasztok!
Létezik-e két olyan valós szám a és b hogy az összegük, a+b irracionális és az a2n+1+b2n+1 racionális minden n N-re? N-re?
|
|
|
|
|
|
|
|
|
|
| [2539] Enkidu | 2008-01-09 12:48:33 |
 Ja igen! Elírtam, de én is igazoltam (sajnos csak magamnak) a multiplikativitást, úgyhogy ez rendben van. Igazából azért bizonytalanodtam el korábban, mert a kapott megoldás "nem valami szép" és nem tudom, hogy Cckek akar(t)-e valami szépet mutatni azzel a feladattal kapcsolatban. Én már ezen agyaltam. Csá!
|
| Előzmény: [2537] nadorp, 2008-01-09 08:32:10 |
|
| [2538] nemtommegoldani | 2008-01-09 11:21:52 |
 Sziasztok! Azt szeretném kérni, valaki írjon ide a fórumra pár "nívósabb" számelméleti feladatot legnagyobb közös osztó, ill. legkisebb közös többszörös témakörben, illetve diofantoszi egyenletek témakörben (pl. olyanokra gondolok, amik OKTV-n, vagy más tanulmányi versenyeken előfordultak már)megoldással együtt. NAgyon köszönöm a segítséget!!! Már több helyen keresgéltem, de nem nagyon találok.
|
|
|
| [2536] Enkidu | 2008-01-07 13:05:07 |
 A következő definícióval élve: 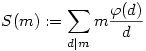 S(m) egy számelméleti függvény. Így prímhatványhelyeken felvett helyettesítési értékei meghatározzák. Ha m=pn,S(m)=pn-1(np+p-n) egyébként pedig a szokásos módon ha (m,n)=1, akkor S(mn)=S(m)S(n). S(m) egy számelméleti függvény. Így prímhatványhelyeken felvett helyettesítési értékei meghatározzák. Ha m=pn,S(m)=pn-1(np+p-n) egyébként pedig a szokásos módon ha (m,n)=1, akkor S(mn)=S(m)S(n).
Most így megnézve lehet, hogy valamit félreértettem, mert túl egyszerű amit írok, de ha már végigszenvedtem a TeX tanfolyamot csak bennhagyom. Hello!
|
| Előzmény: [2535] Cckek, 2008-01-05 12:33:11 |
|
| [2535] Cckek | 2008-01-05 12:33:11 |
 Valóban ez a megoldás, gratulálok, mert ez egyáltalán nem egy könnyű feladat:D, legalábbis számomra nem volt az. Ha már Euler számelméleti függvényénél vagyunk, akkor itt van mégegy:
Számítsuk ki a következő összeget:
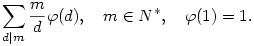
|
| Előzmény: [2534] nadorp, 2008-01-04 23:18:53 |
|
| [2534] nadorp | 2008-01-04 23:18:53 |
 Nem volt unalmas,de szerencsém volt :-). Mindkét oldal "e" alapú logaritmusát véve,bizonyítandó, hogy
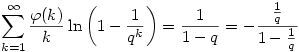
Felhasználva, hogy |q|>1 és a logaritmus függvény hatványsorát ez ekvivalens a következővel
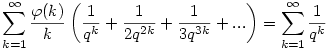 . .
Most vizsgáljuk meg 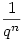 (n (n 1) együtthatóját a bal oldalon. Ha ez mindig 1, akkor készen vagyunk. 1) együtthatóját a bal oldalon. Ha ez mindig 1, akkor készen vagyunk.
Nyilván ha n=ab, akkor lesz olyan tag, ahol az együttható 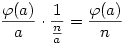 . Tehát . Tehát 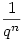 együtthatója a bal oldalon együtthatója a bal oldalon
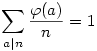 ( Itt felhasználtuk, hogy a ( Itt felhasználtuk, hogy a  (n) számelméleti függvény összegzési függvénye az "n" függvény) (n) számelméleti függvény összegzési függvénye az "n" függvény)
|
| Előzmény: [2532] Cckek, 2008-01-04 18:12:30 |
|
| [2533] Lóczi Lajos | 2008-01-04 20:33:11 |
 "Itt elég a második tagról belátni, hogy pozitív, mert az első az. x=1+t helyettesítéssel t3-ig kiírt Taylor-sorral látszik, nem tudom, van-e rá egyszerűbb módszer, ez az út elég gány ahhoz, hogy végigírjam."
Mivel csak polinom és logaritmus van benne, ilyenkor érdemes még egyszer deriválni:
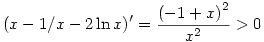 , ha x>1, de x-1/x-2ln x az 1 helyen 0, tehát ha x>1, akkor mindig pozitív a kérdéses kifejezés. , ha x>1, de x-1/x-2ln x az 1 helyen 0, tehát ha x>1, akkor mindig pozitív a kérdéses kifejezés.
|
| Előzmény: [2529] Sirpi, 2008-01-04 17:15:02 |
|
| [2532] Cckek | 2008-01-04 18:12:30 |
 Igen ez is gyors, szép megoldás, az eredeti feladat így szólt: Számitsuk ki ![\left[\frac{(e^\pi+e^e)(\pi-e)}{e^\pi-e^e}\right]](keplet.cgi?k=FF5948E8DC055B1D) -t. -t.
De mivel látom unatkoztok itt van egy sokkal nehezebb feladat amivel rengeteget kinlódtam: Bizonyítsuk be, hogy
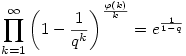
ahol  az Euler indikátor, q az Euler indikátor, q Z\{-1,0,1} Z\{-1,0,1}
|
|
| [2531] Róbert Gida | 2008-01-04 17:57:20 |
 Kijön ez deriválgatásokkal, nálam legyen x:= - - (érdemesebb ezt az utat követni, mert akkor log nem jön be). x a továbbiakban mindig legyen (0,1)-ben. (érdemesebb ezt az utat követni, mert akkor log nem jön be). x a továbbiakban mindig legyen (0,1)-ben.
Ekkor, mivel csak az egészrésze kell a függvénynek, ezért elég igazolni, hogy 2 és 3 közé esik az értéke:  , ha 0<x<1. A nevező pozitív, így felszorzás és rendezés után kapjuk, hogy kell: 0<(3-x)ex-(3+x)=:g(x), de g(0)=0, továbbá g'(x)=(2-x)ex-1, amire g'(x)>ex-1>0, így g szigorúan monoton nő (0,1) intervallumban, de g(0)=0, így g(x)>0 itt, ami kellett. (g folytonossága is kellett itt még, mert sajnos g'(0)=0). , ha 0<x<1. A nevező pozitív, így felszorzás és rendezés után kapjuk, hogy kell: 0<(3-x)ex-(3+x)=:g(x), de g(0)=0, továbbá g'(x)=(2-x)ex-1, amire g'(x)>ex-1>0, így g szigorúan monoton nő (0,1) intervallumban, de g(0)=0, így g(x)>0 itt, ami kellett. (g folytonossága is kellett itt még, mert sajnos g'(0)=0).
Másik irányú becsléshez:  , felszorozva és rendezve kell: 0 , felszorozva és rendezve kell: 0 (x-2)ex+(x+2)=:h(x), itt h(0)=0, továbbá: h'(x)=(x-1)ex+1, tehát h'(0)=0, továbbá h''(x)=xex (x-2)ex+(x+2)=:h(x), itt h(0)=0, továbbá: h'(x)=(x-1)ex+1, tehát h'(0)=0, továbbá h''(x)=xex 0, így h' monoton nő, de h'(0)=0, így h'(x) 0, így h' monoton nő, de h'(0)=0, így h'(x) 0, de akkor h monoton nő, de h(0)=0 miatt h(x) 0, de akkor h monoton nő, de h(0)=0 miatt h(x) 0 teljesül, ami kellett. 0 teljesül, ami kellett.
|
| Előzmény: [2529] Sirpi, 2008-01-04 17:15:02 |
|
|
| [2529] Sirpi | 2008-01-04 17:15:02 |
  -t kiemelve a számlálóból és a nevezőből is, valamint bevezetve az -t kiemelve a számlálóból és a nevezőből is, valamint bevezetve az 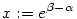 jelölést, a következő (immár egyváltozós) alakot kapjuk - mellesleg az is látszik, hogy jelölést, a következő (immár egyváltozós) alakot kapjuk - mellesleg az is látszik, hogy  és és  pozitív voltát nem használjuk sehol, az a feltétel elhagyható: pozitív voltát nem használjuk sehol, az a feltétel elhagyható:
![f(x):=\left[\frac{x+1}{x-1}\cdot \ln x \right] \qquad 1<x<e](keplet.cgi?k=36069AE35594D1F3)
f(e) 2.16, 2.16, 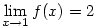 (utóbbi azért igaz, mert az x=1 közelében ln x (utóbbi azért igaz, mert az x=1 közelében ln x x-1) x-1)
Ezek után már csak az kell, hogy a függvény szigorúan monoton az [1,e] intervallumon, és meg is kaptuk a választ: 2.
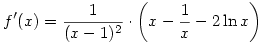
Itt elég a második tagról belátni, hogy pozitív, mert az első az. x=1+t helyettesítéssel t3-ig kiírt Taylor-sorral látszik, nem tudom, van-e rá egyszerűbb módszer, ez az út elég gány ahhoz, hogy végigírjam.
|
| Előzmény: [2528] Cckek, 2008-01-04 16:22:44 |
|
| [2528] Cckek | 2008-01-04 16:22:44 |
 Itt van Lajos, egy neked való feladat, egy helybéli igen megbecsült matematikus egyik feladatát általánosítgattam. Persze bárki megoldhatja ha van kedve hozzá.
Legyen  , , >0,0< >0,0< - - <1. Számítsuk ki <1. Számítsuk ki
![\left[\frac{(e^\beta+e^\alpha)(\beta-\alpha)}{e^\beta-e^\alpha}\right]](keplet.cgi?k=7DD0AB9D56429775)
értéket ahol [x]-el az x valós szám egész részét jelöltük.
|
|
| [2527] Lóczi Lajos | 2007-12-30 15:44:32 |
 Tovább próbálkozom. Legyenek tehát P és Q az n-dimenziós (komplex) Cn teret önmagukba képező n x n-es hermitikus idempotens mátrixok, melyek rangja azonos.
A rang a képtér dimenziója.
Az operátorokra vonatkozó felbontási tétel alapján tudjuk (felhasználva, hogy most az operátoraink hermitikusak és véges dimenzióban vagyunk), hogy Cn előáll a lineáris operátor képtere és magtere direkt összegeként. (Speciálisan, a képtér és a magtér dimenziójának összege n.)
Ezekből azt kapjuk, hogy P-nek és Q-nak nemcsak a képtere, de a magtere is azonos dimeziós kell legyen.
Korábban láttuk, hogy P=PQ. Ebből az adódik, hogy ha egy x vektor Q magterében van, akkor egyúttal P magterében is benne van: ker(Q) ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos. ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos.
De akkor a felbontási tétel miatt az ortogonális komplementereik, vagyis a képtereik is azonos alterek.
Tudjuk, hogy a projektorok a képtéren identitásként hatnak. (Valóban, ha x pl. P képterében van, akkor alkalmas y Cn vektorral x=Py. De az idempotencia miatt ekkor Px=PPy=Py=x.) Cn vektorral x=Py. De az idempotencia miatt ekkor Px=PPy=Py=x.)
Legyen tehát z egy tetszőleges Cn-beli vektor. Ekkor z előáll z0+z1 alakban, ahol z0 P magterébe esik (ami egyúttal Q magtere is), z1 pedig P (avagy Q) képterébe esik. Emiatt
Pz=P(z0+z1)=Pz1=z1=Qz1=Q(z0+z1)=Qz,
tehát P=Q.
Remélem, ezzel a megoldás rendben van :)
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2526] hobbymatekos | 2007-12-30 15:38:23 |
 Nem kőtáblába véstem:-) Azért irtam mert érdekel a téma. Semmi egyéb. Az összes tévedésre szükséges rámutatni. Az összeget azért gondolom oda a definicióhoz, mert igazán az az oldala izgat. Mint ahogy mondtad is a mátrix nyoma fontos.(Fizikailag a nyom sűrűséggel kapcsolatos. A sűrűségek pedig additivek? Vagyis egy térbeli pontban egy részecske helyett rögtön egy r szer akkora?. Helycserével? Anélkül?) Diagonálmátrixok összegének nyoma a nyomok összege. r(a+a)=raa, a mátrix elemei, r komplex számok, szintén megoldható, ekkor persze ferdén hermitikus a mátrix, akkor főátlóban tisztán képzetes szám állhat, de ezek minden páros hatványa lehet hermitikus, idempotens. De ezek csak gondolatok. Az eredeti feladattal kapcsolatban csak annyi volt a meglátásom, hogy a mátrix harmadik hatványa van a bizonyitandóban, akkor PP=P ből következik idempotencia miatt PQP=PQ=QP=PP=P. A középső rész kommutativitás. (Kommutativitásra nxn mátrixnál legalább nxn művelet kell eldöntéséhez. És ha n az Avogadro szám?) Egyébként olvasótok vagyok inkább. BUÉK
|
| Előzmény: [2524] Cckek, 2007-12-30 00:31:48 |
|
| [2525] Lóczi Lajos | 2007-12-30 14:21:01 |
 (Nem kukacoskodásból kérdeztem rá direktben, csak azért, mert nem értettem, és meg akartam érteni az állítását, ehhez tudnom kellett, a definíciókban "közös nevezőn" vagyunk-e :)
|
| Előzmény: [2524] Cckek, 2007-12-30 00:31:48 |
|
| [2524] Cckek | 2007-12-30 00:31:48 |
 Az értelmezéseket valóban kitünően elmondtad, s én hiszek abban hogy ez a forum a matematika és persze a matematikusok feltétlen tiszteletéről szól. Éppen ezért nem árt néha beismerni ha tévedtünk. Ez k...a nehéz de a tisztelet elérése szempontjából feltétlenül szükséges. És nem olyan vészes a tévedés,-a matematikai eredmények tévedések sorozatai, egy tévedés kijavítása oriási eredmény lehet:D- sokkal inkább veszélyes feltétlenül védeni az igazunkat. A magam hibájából tanultam ezt tehát, sértődöttségre semmi ok.
|
| Előzmény: [2523] hobbymatekos, 2007-12-29 02:55:18 |
|
| [2523] hobbymatekos | 2007-12-29 02:55:18 |
 Az I idempotens. Elmondtam az általános definiciot. (Annak értelmében nem lenne idempotens) Mátrixokra A=AA=AAA..... Ez a probléma amit kitűzött a kolléga: PQP=PP=P. Az állitása PQP=P alakban volt megadva. Továbbá csak vázoltam mxn mátrixból kiindulva unitér mátrixra mi adódik. Rang változatlan. Te megcsináltad Projektorra. Kellene még egy szokásos (A+A*)/2 és poláris P=QQU felbontásra is.
|
| Előzmény: [2520] Lóczi Lajos, 2007-12-28 21:08:34 |
|
|
| [2521] Lóczi Lajos | 2007-12-28 21:18:43 |
 Nem értem ezt. Kérlek, mondd ki, mi az állításod és mit bizonyítasz.
"Innen generalizálással adódik az állitás." Ez mit jelent és melyik állítás?
"P=PP=PPP implikálja TQ=TTQ implikáció ugyanaz, mint T=TQT." Ez nem magyar mondat. Kérlek, tisztázd.
Mit jelölsz felső vesszővel?
Stb.
|
| Előzmény: [2519] hobbymatekos, 2007-12-28 00:35:05 |
|
|
| [2519] hobbymatekos | 2007-12-28 00:35:05 |
 Ez már hermitikus és idempotens is. És pozitiv szemidefinit. Diagonizálható. Egy diagonál mátrix pedig triviálisan hermitikus és idempotens, ha elemei valósak (csak ekkor hermitikus definició szerint). Legyen M mxn mátrix, rangja n. És oszlopai ortonormáltak, P=MM' hermitikus,ha főátlóbeli elemei valósak, továbbá ortonormáltság miatt M'M=I , nxn es identitás. Létezik U unitér mátrix, T=U'PU. Mivel P hermitikus, T is az. PP=P implikálja TT=T, hiszen minden diagonális elem 1 vagy nulla és a rang ugyanannyi marad, azaz T n db 1 est és m-n db nullát tartalmaz főátlójában. Azaz P=UTU'=UTTU=UT'U'UT'U=MM' és M olyan mátrix, hogy n oszlopa U beli. Innen generalizálással adódik az állitás. Q rangja ugyanannyi mint P nek, valamint hermitikus idempotens.
P=PP=PPP implikálja TQ=TTQ implikáció ugyanaz, mint T=TQT.
|
| Előzmény: [2518] Cckek, 2007-12-26 14:17:40 |
|
|
|
| [2516] Cckek | 2007-12-26 13:08:46 |
 Hmm, szerinted tehát csak O illetve I idempotens? Amugy az idempotencia ebben az esetben a sor/oszlop mátrixszorzásra vonatkozik, s gondolom ott követted el a hibát hogy így ültetted át az értelmezést: x (G,*) idempotens, ha x*x=x, most pedig a *-ot sorra a + illetve . műveletekkel helyetesítetted. Keress olyan négyzetes másodrendű mátrixokat melyeknek nyoma 1 determinánsa 0. Ezek mind idempotensek lesznek:D (G,*) idempotens, ha x*x=x, most pedig a *-ot sorra a + illetve . műveletekkel helyetesítetted. Keress olyan négyzetes másodrendű mátrixokat melyeknek nyoma 1 determinánsa 0. Ezek mind idempotensek lesznek:D
pl: 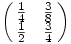
|
| Előzmény: [2515] hobbymatekos, 2007-12-26 12:43:15 |
|
| [2515] hobbymatekos | 2007-12-26 12:43:15 |
 A nullelem idempotens az összeadás és szorzás binér műveletre. A nullelemtől különböző elemek közül csak az egységelem idempotens és csak a szorzásra nézve. Mivel az állitás csak szorzást tartalmaz, ezért 0 vagy egységelemre teljesülhet az idempotencia. Az állitás a hermitikus mátrixok körében csak a valós P=Q=0 vagy P=Q=I mátrixokra igaz. De nem igaz, hogy csak P=Q-ra igaz. Ha Q=I akkor tetszőleges P re igaz. Ha P=0 akkor tetszőleges Q ra igaz. Q=0 ra nem igaz.
|
| Előzmény: [2513] Cckek, 2007-12-26 01:02:06 |
|
|
|
|
|
|
| [2509] hobbymatekos | 2007-12-25 23:25:13 |
 Def.: A idempotens ha A+A=AA=A.
A feltétel szerint P, Q hermitikus és idempotens volt. P=QP egyenlőség tetszőleges nem elfajuló (detP vagy detQ nem nulla) mátrixokra pl: Q=I lenne, de I nem idempotens.
|
| Előzmény: [2508] Lóczi Lajos, 2007-12-25 21:42:39 |
|
| [2508] Lóczi Lajos | 2007-12-25 21:42:39 |
 Nem egészen értem, mit írsz.
"Def.: A idempotens ha A+A=AA=A A feltétel szerint P, Q hermitikus és idempotens volt P=QP egyenlőség tetszőleges nem elfajuló (detP vagy detQ nem nulla) mátrixokra pl: Q=I lenne, de I nem idempotens."
Át tudnád ezt fogalmazni magyarosabbra? Összefolynak a részek. Amúgy miért veszed bele az idempotens definíciójába az összeget?
|
| Előzmény: [2505] hobbymatekos, 2007-12-25 17:05:24 |
|
|
|
| [2505] hobbymatekos | 2007-12-25 17:05:24 |
 Egyelőre csak a következőt sikerült igazolnom: P=PQ=QP Ez segédtételből következik: Ha P és Q hermitikus, akkor PQ=QP(kommutativitás) továbbá P ill. Q idempotens (a feltételek szerint) Def.: A idempotens ha A+A=AA=A A feltétel szerint P, Q hermitikus és idempotens volt P=QP egyenlőség tetszőleges nem elfajuló (detP vagy detQ nem nulla) mátrixokra pl: Q=I lenne, de I nem idempotens. Hermitikus, idempotens mátrixokra Q=P.
|
| Előzmény: [2399] Lóczi Lajos, 2007-10-22 12:32:28 |
|
| [2504] Cckek | 2007-12-24 16:57:02 |
 Kellemes, boldog és békés Karácsonyt minden tisztelt forumozónak. ...és a piával csak Lebesque mértékkel:D
|
|
| [2503] Lóczi Lajos | 2007-12-24 02:16:45 |
 Igen, a feladat érdekessége abban van, hogy indukcióval közvetlenül nem jön ki, viszont egy nála erősebb állítás igen: ha a jobb oldalra  -et írunk, az indukció már végigmegy. -et írunk, az indukció már végigmegy.
|
| Előzmény: [2501] Csimby, 2007-12-24 01:26:49 |
|
| [2502] rizsesz | 2007-12-24 01:30:03 |
 pedig van indukciós, csak sajna nem saját :( úgyhogy nem dobom be a közösbe (viszon Csimby megoldása szép!).
más kérdés: az első 2n pozitív egész számból kiválasztunk k. mekkora k értéke, ha tudjuk, hogy k-ra igaz, hogy van a k szám között 3 olyan, amelyek közül az egyik a másik kettő összege, továbbá az is igaz, hogy ez már k-1 esetén nem teljesül?
|
| Előzmény: [2501] Csimby, 2007-12-24 01:26:49 |
|
|
|
|
|
| [2497] Gyöngyő | 2007-12-22 11:08:52 |
 Sziasztok!
Segítséget szeretnék kérni! Az lenne a kérdésem,hogy hol találok olyan feladatokat,amiben a teljes indukció kicsit furcsa modon kerül elő vagy nem teljesen követi a megszokott utat!
Köszönettel: Zsolt
|
|
|
| [2495] Cckek | 2007-12-14 22:43:57 |
 Krimirajongóként, anélkül hogy kötekedni akarnék, megkérdem, hogy nem Moriarty professzorról van szó? Amúgy nagyon érdekes feladat, én léggyel meg pókhálóval tudom, a pók útolérheti a legyet ha a pókháló tartalmaz háromszöget.
|
| Előzmény: [2492] Enkidu, 2007-12-12 12:45:22 |
|
|
| [2493] Lóczi Lajos | 2007-12-14 00:04:44 |
 Van-e olyan kétváltozós f függvény, hogy 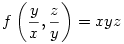 , azaz kifejezhető-e xyz, mint y/x és z/y függvénye? , azaz kifejezhető-e xyz, mint y/x és z/y függvénye?
|
|
| [2492] Enkidu | 2007-12-12 12:45:22 |
 A megoldásod teljesen jó! A 15-ös korlátot csak azért adtam, mert matekórán játszottunk párat gyerekekkel, én sem tudom pontosan, mennyi a legkevesebb lépés (ha Mortimer jól játszik); a lényeg az, hogy ha Holmes áthalad Rejkjavikon, akkor (állandóan közelítve Mortimerhez) 7-8 lépés alatt elkapja.
Szóval ez tényleg csak egy egyszerű játék volt, és nagyon hasonló a megoldása (Rejkjavik nélkül a gráf 2-színezhető lenne - Rejkjavikkal a kromatikus szám 3) is mint a korábbi példának, azért gondoltam, hogy megmutatom.
Sziasztok!
|
| Előzmény: [2491] HoA, 2007-12-11 14:19:06 |
|
| [2491] HoA | 2007-12-11 14:19:06 |
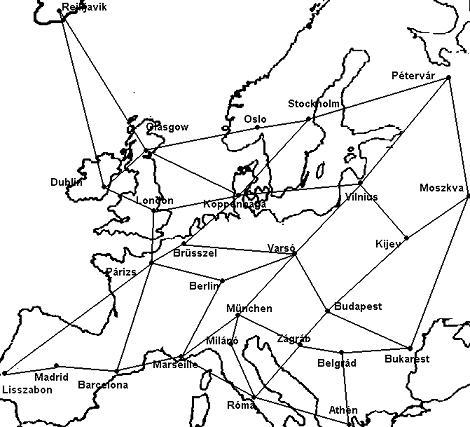
 A Holmes vs. Mortimer feladatban [2479] ezek után világos, hogy ha Rejkjavikot egyik sem érinti, Holmes Pétervárról, Mortimer Párizsból indul és Holmes lép elsőnek, akkor Holmes soha sem léphet abba a városba, ahol éppen Mortimer van. ( Fordítva igen, de Mortimernek ez nyilván nem célja. ) A megoldásnak tehát szükséges feltétele, hogy egyikük érintse egyszer Rejkjavikot. ( Precízen: A két ellenfél rejkjaviki utazásainak száma különböző paritású legyen ) . A továbbiakat nem látom. Hol jön be a 15-ös lépéskorlát? Biztos, hogy nincsenek szigorúbb feltételek? Pl. Mortimer nem mehet kétszer ugyanabba a városba? Az elfogás vége is világos: Ha Mortimer "A" városban van mikor Holmesnak sikerül "B" városba lépnie úgy, hogy "A" minden szomszédja egyben "B" -nek is szomszédja, Holmes nyert. Ilyen például A = Madrid B = Párizs. De hogyan kényszerítheti Mortimert ilyen lépésre? Szabad a gazda.
|
| Előzmény: [2479] Enkidu, 2007-12-05 13:31:00 |
|
| [2490] HoA | 2007-12-07 15:17:43 |
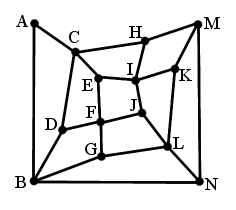
 Én [2476] -ban arra céloztam, hogy ha behúzzuk az AM élt, G gráfunkból egy szép szimmetrikus G' gráfot kapunk, ahol minden csúcs fokszáma 3 vagy 4, és a 8 éves is könnyen észreveheti, hogy 3-adfokú csúcsnak csak 4-edfokú szomszédja van és viszont. Innen adódik a 8 piros - 6 zöld alapú megoldás. És persze ha G' -nek nincs Hamilton útja, akkor G-nek sem lehet.
|
| Előzmény: [2489] Csimby, 2007-12-07 02:21:30 |
|
| [2489] Csimby | 2007-12-07 02:21:30 |
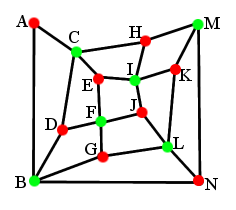
 A színezésből látszik, hogy két piros ill. két zöld csúcs között nem megy él, hanem él csak piros és zöld csúcsok között megy. Így bármely úton/körön felváltva kell hogy következzenek a piros ill. zöld csúcsok. De mivel piros csúcsból 8, zöld csúcsból pedig csak 6 van így váltakozó piros-zöld sorozatból legfeljebb csak 13 hosszút tudunk csinálni. Azt pedig, hogy a gráf kétszínnel színezhető - vagyis páros - lehetett megsejteni abból, hogy benne minden kör páros volt, ez a két állítás ekvivalens. Persze csak abból, hogy a gráf páros még nem következik hogy nincs benne Hamilton út, ehhez még kellett, hogy a két osztály (piros és zöld csúcsok) elemszámának a különbsége 2.
|
| Előzmény: [2488] szbela, 2007-12-07 01:38:08 |
|
| [2488] szbela | 2007-12-07 01:38:08 |
 Sziasztok!
Ez egy olyan megoldás lenne, ahol arra a tételre hivatkozol, hogy ha van a gráfban Hamilton-kör, akkor k csúcs és az ezekből induló élek elhagyásával a gráf legfeljebb k komponensre esik szét? A zöld (6db) pontok elhagyásával a gráf 8 db komponensre esik szét, azaz nincs Hamilton-köre.
|
| Előzmény: [2485] jonas, 2007-12-06 19:41:31 |
|
|
|
|
| [2484] Csimby | 2007-12-06 19:30:59 |
 Nem kell program. Van "szép" megoldás is, tehát nem ilyen esetszétválasztgatós. Mondjuk nekem hogy rájöjjek kellett valami amit véges matekon tanultunk az egyetemen.
|
|
| [2483] jonas | 2007-12-06 19:22:38 |
 Lefuttattam rá egy kimerítő keresést. Nem volt nehéz, mivel csak 14 csúcs van, és minden csúcsból csak legfeljebb három irányba lehet továbbmenni.
Ha helyes a programom, akkor nincs benne Hamilton-út.
Ha megengedjük, hogy egy csúcsot kihagyjunk, akkor pl. a következő útvonal jó: ACHMNLKIJFGBD.
|
| Előzmény: [2467] Csimby, 2007-12-04 01:26:25 |
|
|
|
| [2480] Enkidu | 2007-12-05 13:41:13 |
 A bizonyítás:
Nyolc ember között van olyan, aki legalább négy másikat elvert. Ő lesz a győztesünk. Vizsgáljuk azt a négy embert, akiket megvert. Ezen négyesben van olyan ember, aki a másik három ember közül kettőt elvert, ő lesz a "második". Az a két ember, akiket ez az utóbbi elvert eldöntik egymás között, ki a harmadik és a negyedik. Ezzel kész.
Ha hét emberre vizsgálnánk, akkor már nem feltétlenül teljesül; ha pl (megszámozva a versenyzőket) mindenki elveri a nála 1,2 és 4-gyel nagyobb sorszámút (modulo 7 gondolkozva - ennyi pontatlanság talán belefér:)), akkor az egy ellenpélda.
|
| Előzmény: [2466] Csimby, 2007-12-04 01:19:45 |
|
| [2479] Enkidu | 2007-12-05 13:31:00 |
 Egy ezzel a példával kapcsolatos aranyos (bár elég egyszerű) példa a következő:
Sherlock Holmes ősi ellenfele Mortimer ellopta a Mona Lisát a párizsi Louvre-ból. Holmes éppen Péterváron volt és rögtön repülőre ült, hogy elkapja a gazfickót. (Európa repülőtereit a lenti ábra mutatja; egy lépésben csak egy szomszédos repülőtérre repülhetünk, azaz pl Pétervárról közvetlenül csak Moszkva, Vilnius és Stockholm érhető el.) Miután Holmes lépett egyet Mortimernek is lépnie kell (ha túl sokáig maradna egy helyen elkapnák a rendőrök). Vagyis a két játékos felváltva lép. Ha Holmesnak sikerül ugyanabba a városba repülnie, ahol éppen akkor Mortimer tartózkodik, akkor elkapja és vége a játéknak. Ha Mortimer 15 lépés után is szabad, végleg megmenekült. El lehet-e fogni Mortimert? Ha igen, hogyan?
|
 |
| Előzmény: [2468] rizsesz, 2007-12-04 08:45:58 |
|
|
|
| [2476] HoA | 2007-12-05 11:11:43 |
 Nem is tudom, most örüljek-e, hogy sikerült rájönni egy megoldásra, amihez valóban elég egy 8 éves tudása. Az ebben a megoldásban felhasznált tulajdonság felismeréséhez nem a 10 négyszög léte, hanem az segít, ami hiányzik az ábráról :-)
|
| Előzmény: [2474] rizsesz, 2007-12-04 14:05:10 |
|
|
|
| [2473] Hajba Károly | 2007-12-04 14:01:11 |
 A vonalak 10 db négyszöget határoznak meg. Ha ezeket átalakítjuk egy újabb gráffá úgy, hogy a négyzetek a gráfcsúcsok és a csatlakozó él az új gráf élei, akkor ebben a gráfban is meg kellene tudni csinálni az összekötést. Ha nem sikerül, akkor az eredetiben sem lehet.
Persze tudom ez nem bizonyítás. Inkább csak morfondíroztam egyet. :o)
|
| Előzmény: [2471] Csimby, 2007-12-04 12:47:51 |
|
| [2472] rizsesz | 2007-12-04 13:58:02 |
 Akkor gondolj arra, hogy a hivatalos megoldás tulajdonosa 2. osztályos volt. És nem középiskolás, hanem általános iskolás, azaz 8 éves. Szóval érdemes elrugaszkodni egy kicsit attól, amit az ember tud, és olyan fejjel gondolkodni, mintha csak nagyon alapvető eszközeink lennének. :)
|
| Előzmény: [2470] Hajba Károly, 2007-12-04 12:38:43 |
|
| [2471] Csimby | 2007-12-04 12:47:51 |
 Szerintem is egy szép feladat :-) Ha alég sokáig nézi az ember a gráfot, akkor észre lehet venni valamit ami nagyon sokat segít.
|
|
| [2470] Hajba Károly | 2007-12-04 12:38:43 |
 Elvileg ez egy nyílt Hamilton-kör lenne, amire nincs egyértelmű megoldhatósági kritérium, mint az Euler-körre van. Nekem úgy tűnik, nem létezik Hemilton-kör, de a gráfok mélységében nem vagyok eléggé járatos, így nem tudom bizonyítani.
|
| Előzmény: [2467] Csimby, 2007-12-04 01:26:25 |
|
|
|
|
| [2466] Csimby | 2007-12-04 01:19:45 |
 Láttam most egy hasonlót (legalábbis annyiban hasonlít, hogy körmérkőzéses :-):
330.feladat 8-an körmérkőzést játszanak (nincs döntetlen). Biz.be, hogy mindig kiválasztható 4 olyan versenyző, akik közül az első legyőzte a másodikat, harmadikat és negyediket, a második legyőzte a harmadikat és negyediket, valamint a harmadik legyőzte a negyediket.
|
| Előzmény: [2439] rizsesz, 2007-11-23 10:23:55 |
|
|
| [2464] HoA | 2007-11-27 18:36:33 |
 Egy másik megoldás a 6 versenyzőre: Legyen a(z egyik) győztes A. Mivel összesen 6 x 5 / 2 = 15 pontot osztanak ki (sakk) , neki legalább 2.5 pontja van. Vegyük az A-t tartalmazó párok P halmazát ( 5 pár ) és a P párokat legyőzők G halmazát . G nem lehet 1 elemű, mert akkor saját magát is le kellene győznie. De nem lehet 3 vagy több elemű sem, mert akkor A-t legalább hárman legyőzték volna, tehát nem lehetne csak 5-3 = 2 pontja. Ha viszont G kételemű, akkor G tagjai A-tól 2, a többi 5 résztvevőtől együtt legalább 5 pontot szereztek, így együtt legalább 7 pontjuk van, az egyiknek legalább 3.5. A viszont a 2 pont elvesztésével legfeljebb 3 pontos lehet, ami ellentmond annak, hogy ő a(z egyik) győztes.
|
| Előzmény: [2439] rizsesz, 2007-11-23 10:23:55 |
|
|
| [2462] Enkidu | 2007-11-27 13:23:05 |
 A hétszereplős kőrmérkőzésre a válasz: lehetséges.
A következő táblázat mutat egy lehetséges esetet: az egyes sorokban azt jelöltem, hogy az adott játékost ki verte meg.
1| 2,3,4 (2,3 és 4 veri az 1-est) 2| 3,6,7 3| 4,5,7 4| 2,5,6 5| 1,2,7 6| 1,3,5 7| 1,4,6
A példád továbbgondoltam 7-nél több szereplő esetére.(Nem lesz valami nagy durranás) Szóval ekkor is megoldható, hogy bármely 2-höz legyen aki veri mindkettőt. Pl. az összes többit verje a 2,3,4-es (az első 7-en kívűli összes többit). Ez nyilván megfelelő.
Sziasztok!
|
| Előzmény: [2438] nadorp, 2007-11-23 08:10:45 |
|
|
| [2460] Sirpi | 2007-11-27 11:01:14 |
 Köszi, sokat segítettél :-)
Emiatt a 396 miatt egyrészt leesett az állam, másrészt arra is rájöttem, hogy ennek fényében nem biztos, hogy érdemes túl sok időt belefeccölnöm a probléma vizsgálatába...
Ja, és itt egy példa, amikor páratlan sok elem tölti ki a téglalapot (bár nem minimális), ezt hirtelen találtam, lehet, hogy van kisebb is.
|
| Előzmény: [2459] Hajba Károly, 2007-11-27 01:09:54 |
|
|
|
|
| [2456] Sirpi | 2007-11-26 15:38:24 |
 Igazad van, ez kimaradt. Én úgy vettem, hogy lehet tükrözni. Bár az is érdekes lehet, hogy milyen különbség adódhat egy adott alakzat esetén, ha megengedjük, illetve ha nem engedjük meg a tükrözést.
És igen, én is 10-est találtam még az 1,2,4-en kívül. Vajon van más?
|
| Előzmény: [2454] Hajba Károly, 2007-11-26 14:26:42 |
|
|
|
| [2453] Sirpi | 2007-11-26 12:53:02 |
 Felmerült bennem egy probléma, egyelőre csak ízlelgetem. Az egyszerűség kedvéért nevezzünk rácsidomnak rácsnégyzetekből álló, élek mentén illeszkedő, összefüggő alakzatokat (gondoljatok a tetrisre, de nem feltétlen kell 4 kis négyzetből állnia az alakzatnak). Ezek között vannak olyanok, amiket többször felhasználva ki lehet rakni egy téglalapot, másokból meg nem. Az előbbiekhez rendeljük hozzá az ehhez szükséges minimális darabszámot. Tehát ha az alakzat eleve téglalap, akkor 1-et, a tetrisben pedig pl. az L-alakhoz 2-t, a T-alakhoz 4-et rendelünk.
A kérdés az, hogy mekkora lehet maximálisan ez a szám? Vagy egyáltalán, milyen más értékek adódhatnak így?
Mindenesetre találtam 4-nél nagyobbat már, innen jött az ötlet.
|
|
| [2452] Lóczi Lajos | 2007-11-25 22:46:37 |
 Nem olyan nehéz ez.
Tudjuk, hogy x, y és z pozitívak. Az x g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B 0, A>0, B>0. 0, A>0, B>0.
Azt kapjuk, hogy
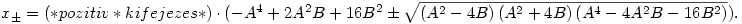
Ki akarjuk zárni, hogy g<0 pozitív x-ekre.
Ha a diszkrimináns negatív, készen vagyunk.
Ha a diszkrimináns A2-4B miatt nulla, szintén készen vagyunk, mert ez annak felel meg, ha y=z, de 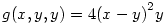 . .
Elég tehát az A4-4A2B-16B2 0 esetben megvizsgálni, hogy a nagyobbik gyök, x+ lehet-e pozitív. 0 esetben megvizsgálni, hogy a nagyobbik gyök, x+ lehet-e pozitív.
Elemi módon látszik, hogy A4-4A2B-16B2 0 és -A4+2A2B+16B2 0 és -A4+2A2B+16B2 0 és A2-4B 0 és A2-4B 0 egyszerre nem teljesülhetnek a pozitív számpárok körében. 0 egyszerre nem teljesülhetnek a pozitív számpárok körében.
Az kell tehát csak megnézni, mi van, ha -A4+2A2B+16B2 0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van. 0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van.
|
| Előzmény: [2450] Lóczi Lajos, 2007-11-25 20:32:12 |
|
| [2451] Róbert Gida | 2007-11-25 20:51:55 |
 Igen, ezt kell belátni, nem szabadott volna négyzetre emelnem, mert a jobb oldal negatív is lehet, köszönhetően annak, hogy: igaz, hogy R 2*r teljesül, de R bármekkora lehet rögzített r mellett. 2*r teljesül, de R bármekkora lehet rögzített r mellett.
Egyébként szabályos háromszögre egyenlőséggel, ez megfelel x=y=z-nek és g(x,x,x)=0
|
| Előzmény: [2450] Lóczi Lajos, 2007-11-25 20:32:12 |
|
|
|
| [2448] Róbert Gida | 2007-11-25 16:29:22 |
 Hm, a polinom lexikografikusan legnagyobb tagjának negatív az együtthatója, ergó számtani-mértani egyenlőtlenségekkel ezt nem lehet belátni.
A polinom egyébként homogén hatodfokú, így feltehető például, hogy x=1 teljesül. (Kicsivel rövidebb lesz akkor a képlet.)
|
| Előzmény: [2446] Róbert Gida, 2007-11-25 16:14:49 |
|
|
| [2446] Róbert Gida | 2007-11-25 16:14:49 |
 A következőkkel próbálkoztam:
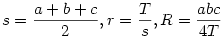
Majd egy háromszögekre való egyenlőtlenség bizonyításának ismert technikája: legyen
x=s-a,y=s-b,z=s-c
Ekkor x,y,z>0 teljesül, megfordítva minden pozitív x,y,z-re tartozik pontosan egy háromszög. (oldalaira a háromszög-egyenlőtlenség teljesül). Ezt beírva és négyzetre emelve és rendezve az oldalt kapjuk: f(x,y,z)=4yz(x+z)2(x+y)2-(16xyz-(x+y)(y+z)(z+x))2 kell teljesülnie minden pozitív x,y,z számokra. Ez a polinom viszont a maple szerint irreducibilis a racionális többváltozós test felett. Egy nehéz módszer ilyenkor, hogy számtani-mértani egyenlőtlenségek tucattyaival igazolni, hogy f(x,y,z) pozitív, de ennek a megtalálása egyáltalán nem triviális, illetve van amikor nem is lehetséges, annak ellenére, hogy az egyenlőtlenség igaz.
|
| Előzmény: [2443] Gyöngyő, 2007-11-25 13:26:07 |
|
|
|
| [2443] Gyöngyő | 2007-11-25 13:26:07 |
 Sziasztok!
Lenne egy kis feladatom,amivel nem nagyon tudok megbirkozni:
adva van egy általános háromszög ahol r,R a szokásos dolgok.p=kerület fele,a,b,c az oldalak hossza. Bizonyítsuk be,hogy:
a/2*((4r-R)/R)=<gyok((p-b)(p-c).
Köszönettel:
Zsolt
|
|
| [2442] Python | 2007-11-25 12:37:22 |
 a.) Nem lehet. Ha A-t csak 2 ember, B és C győzte le, akkor A-t és B-t mindkettőjüket csak C győzhette le, így B-t C legyőzi, de A-t és C-t csak B győzhette le, így C-t B legyőzi, de ez ellentmondás, így mindenkit legalább 3-an legyőznek, de ehhez 6.3=18 meccs kell, de csak 15 meccs van.
|
| Előzmény: [2439] rizsesz, 2007-11-23 10:23:55 |
|
| [2441] kisevet7 | 2007-11-23 15:26:42 |
 Sziasztok! Köszönöm a megoldásokat! Sajnálom, hogy nem voltam gépnél az előző 2 napban, így nem tudtam válaszolni a kérdésekre, de természetesen a szimmetria miatt (mármint hogy mindenki kaszabolja a másikat, csak más hatákonysággal) igaz a másik összefüggés is. Sirpi! Esetleg találkoztál azzal az ese4ttel is, ahol az egyik csapat hagyományosan kaszabol, a másik gerillaharcot folytat (amikoris a gerillákat meg is kell keresni), és ahol az összefüggés x'(t)=bx(t)y(t)? (x harcol hagyományosan, y a gerilla)
|
|
| [2440] Sirpi | 2007-11-23 14:25:47 |
 Az integrálással kapott egyenleted átrendezve:
ay2(t)-bx2(t)=ay2(0)-bx2(0)
Vagyis az f(t)=ay2(t)-bx2(t) függvény igazából nem függ t-től, és értéke ugyanannyi, mint kezdetben.
Ebből pl. kijön az a szerintem meglepő dolog, hogy egy 5000-es és egy 4000-es sereg ütközetekor (azonos tudású katonákat feltételezve) a győztes csapatnak 3000(!) katonája marad életben. 13000 vs. 12000 esetén pedig 5000.
Én biztos, hogy magamtól sokkal kevesebbre tippeltem volna (korábban magam is felvetettem és megoldottam ezt a feladatot, és már akkor megdöbbentett az eredmény).
|
| Előzmény: [2434] wernerm, 2007-11-21 22:19:43 |
|
| [2439] rizsesz | 2007-11-23 10:23:55 |
 Sziasztok!
Lehetséges-e az egy a., 6, b., 7 fős társaságban, ahol mindenki játszik mindenkivel (mondjuk sakkoznak) hogy bármely 2 emberhez található egy olyan 3., aki megverte mindkettejüket?
|
|
| [2438] nadorp | 2007-11-23 08:10:45 |
 Bocs, helyesen:
Gondolom a feladat úgy van modellezve, hogy az y sereg egy katonája mondjuk percenként "a" darab ellenséget tud legyőzni, az x sereg egy katonája pedig percenként "b" darabot és feltesszük, hogy ezt egyenletesen teszik.
|
| Előzmény: [2437] nadorp, 2007-11-23 08:06:15 |
|
| [2437] nadorp | 2007-11-23 08:06:15 |
 Gondolom a feladat úgy van modellezve, hogy az y sereg mondjuk percenként "a" darab ellenséget tud legyőzni, az x sereg pedig percenként "b" darabot és feltesszük, hogy ezt egyenletesen teszik.
|
| Előzmény: [2436] wernerm, 2007-11-22 22:22:09 |
|
| [2436] wernerm | 2007-11-22 22:22:09 |
 Ha nem lenne az az egyenlet, akkor tetszőleges y(t)-t beírhatnék, és abból x(t)-t integrálással kapnám.
A feladat kitűzője valóban nem írt y'(t) és x(t) közötti összefüggésről, de mivel két hadseregről van szó, a dolog elég szimmetrikusnak tűnik, ezért tettem fel egy ilyen alakú egyenletet.
üdv: Miklós
|
| Előzmény: [2435] Lóczi Lajos, 2007-11-22 11:44:44 |
|
|
| [2434] wernerm | 2007-11-21 22:19:43 |
 Nézzük meg, hogy az idő elteltével egymáshoz viszonyítva hogyan változnak a hadseregek. (A pontos időbeli lefutás nem lényeges, csak az a lényeg, ki nyer.)
x'(t)=-ay(t)
-bx(t)=y'(t)
Szorozzuk össze a két egyenletet!
ay(t)y'(t)=bx(t)x'(t)
Integráljuk mindkét oldalt 0-tól t-ig határozottan.
ay2(t)/2-ay2(0)/2=bx2(t)/2-bx2(0)/2
.
Átrendezve ez az x-y síkon egy hiperbola egyenlete. A végső állapotot az jelenti, ha elmetszük valamelyik tengelyt. Amelyik tengelyt elmetszettük, az a sereg győzött. (Nekik maradt katonájuk).
Az x csapat győz, ha bx2é(0)-ay2(0)>0, fordított relációnál az y csapat.
Érdekes a helyzet az egyenlőségnél. Ekkor a két sereg kölcsönösen lekaszabolja egymást.
A katonák kis létszáma esetén lényegessé válik az, hogy a katonák száma egész.
|
| Előzmény: [2433] kisevet7, 2007-11-21 20:48:07 |
|










 -vel egy kiválasztott koordinátatengelyre merőleges hipersíknak és a szimplex origóval szemközti lapsíkjának a szögét gondoltam jelölni.
-vel egy kiválasztott koordinátatengelyre merőleges hipersíknak és a szimplex origóval szemközti lapsíkjának a szögét gondoltam jelölni.  BB1
BB1
 =0,
=0, =-1/2 helyen vesz fel. Ez következik a
=-1/2 helyen vesz fel. Ez következik a 
 (-1,1), és legyen f(-1)=f(0)=f(1)=0, majd ezt terjesszük ki 2-periodikus függvénnyé az egész számegyenesre. Adjuk meg f Fourier-sorának összegfüggvényét.
(-1,1), és legyen f(-1)=f(0)=f(1)=0, majd ezt terjesszük ki 2-periodikus függvénnyé az egész számegyenesre. Adjuk meg f Fourier-sorának összegfüggvényét. (6*m)<
(6*m)<

 B
B 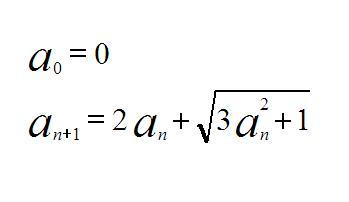
 b, akkor
b, akkor 
 2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés".
2n2 és az arc tg monoton nő, akkor kijön az "alulról a második sorban levő" asszimptotikus egyenlőség. Az utolsó egyenlőséget pedig az előbb írtam le. Egyetértek Lóczi Lajossal, ez nem éppen egy "tesztkérdés". >0-hoz létezik N, ha n>N, akkor
>0-hoz létezik N, ha n>N, akkor 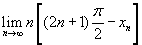

 kéne?
kéne? 


 függvénynél járunk, anno olvastam egy cikket ( Ruzsa Imre: Számelméleti függvények I.) és itt szerepel egy érdekes konstrukció. A poén az benne, hogy a multiplikatív
függvénynél járunk, anno olvastam egy cikket ( Ruzsa Imre: Számelméleti függvények I.) és itt szerepel egy érdekes konstrukció. A poén az benne, hogy a multiplikatív 
 2.16,
2.16,  x-1)
x-1)  ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos.
ker (P). De a két magtér, mint altér, azonos dimenziójú, ez csak úgy lehet, ha azonos.  A=A-A=O(n) az-az az "idempotencia feltételed" csak a nullmátrixra teljesül.
A=A-A=O(n) az-az az "idempotencia feltételed" csak a nullmátrixra teljesül.


 g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B
g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B
