|
|
| [3431] Róbert Gida | 2011-02-18 16:31:25 |
 f(x,0)=g(x)h(0) és f(0,y)=g(0)h(y), innen, ha teljesül a feltétel és g(0)h(0) 0, akkor 0, akkor 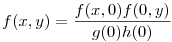 , azaz f(x,y)=Cf(x,0)f(0,y), ahol C konstans. Megfordítva, ha ez utóbbi feltétel teljesül, akkor van alkalmas g,h függvényünk: g(x)=Cf(x,0) és h(y)=f(0,y) , azaz f(x,y)=Cf(x,0)f(0,y), ahol C konstans. Megfordítva, ha ez utóbbi feltétel teljesül, akkor van alkalmas g,h függvényünk: g(x)=Cf(x,0) és h(y)=f(0,y)
|
| Előzmény: [3428] Lóczi Lajos, 2011-02-12 04:02:26 |
|
|
|
| [3428] Lóczi Lajos | 2011-02-12 04:02:26 |
 Adjunk (minél egyszerűbb és jól kezelhető) feltételt arra nézve, hogy egy f kétváltozós függvény mikor áll elő f(x,y)=g(x)h(y) alakban, alkalmas egyváltozós g és h függvényekkel.
|
|
| [3427] jonas | 2011-01-26 21:43:17 |
 Az 513. feladathoz először lássunk be egy rekurziót az U mátrix elemeire. Ez a C mátrixnál segített, tehát gondolhatjuk, hogy itt is beválik. Az összefüggés az lesz, hogy
un+1,k=2un,k-1-un-1,k
feltéve, hogy 1 k. A k=0 esetre egyszerűen un+1,k=un-1,k. Ez egyszerűen abból következik, hogy a másodfajú Csebisev-polinomokra igaz a következő rekurzió. k. A k=0 esetre egyszerűen un+1,k=un-1,k. Ez egyszerűen abból következik, hogy a másodfajú Csebisev-polinomokra igaz a következő rekurzió.
Un+1(x)=2xUn(x)-Un-1(x)
Lássuk be ez utóbbit. Helyettesítsünk be x=cos  -t. (Hogy így esetleg nem minden x kapható meg, az lényegtelen, mert mindkét oldal polinom, tehát elég csak egy intervallumon belátni, hogy egyenlők.) Szorozzuk meg mindkét oldalt sin -t. (Hogy így esetleg nem minden x kapható meg, az lényegtelen, mert mindkét oldal polinom, tehát elég csak egy intervallumon belátni, hogy egyenlők.) Szorozzuk meg mindkét oldalt sin  -val. Így a következő azonosságot kell belátnunk. -val. Így a következő azonosságot kell belátnunk.
sin ((n+2) )=2cos )=2cos  sin ((n+1) sin ((n+1) )-sin (n )-sin (n ) )
Ehhez pedig csak használjuk a sin ( + + )=sin )=sin  cos cos  +sin +sin  cos cos  képletet. Valóban: képletet. Valóban:
sin ((n+2) )=cos (2 )=cos (2 )sin (n )sin (n )+sin (2 )+sin (2 )cos (n )cos (n )=(-1+2cos2 )=(-1+2cos2 )sin (n )sin (n )+2sin )+2sin  cos cos  cos (n cos (n )= )=
=2cos  (sin (sin  cos (n cos (n )+cos )+cos  sin (n sin (n ))-sin (n ))-sin (n )=2cos )=2cos  sin ((n+1) sin ((n+1) )-sin (n )-sin (n ). ).
Innen már megpróbálhatjátok ti kitalálni az 513. bizonyítását – az eredményt megsejteni könnyű, csak ki kell számolni kis értékekre.
|
| Előzmény: [3368] jonas, 2010-11-23 22:19:07 |
|
| [3426] jonas | 2011-01-24 20:13:24 |
 Akkor PAL érdeklődésére tekintettel nézzük meg ezeket a feladatokat.
Kezdjük az 512. feladattal. Stray dog már elárulta a megoldást: a determináns 1. Ezt nem is nehéz belátni: detH=det(CCT)=(detC)2. Csakhogy C háromszögmátrix, mivel ha 0 n<k, akkor n-k<0 és n-k-2<0, így n<k, akkor n-k<0 és n-k-2<0, így
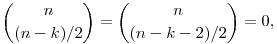
tehát a C mátrix főátló fölötti elemei valóban nullák. Hasonlóan, ha 0 n=k, akkor n=k, akkor
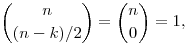
viszont
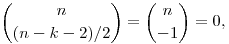
így hát cn,k=1, tehát a mátrix főátlójában egyesek állnak. Ebből aztán detC=1 tehát valóban detC=1.
Mindezt persze akkor lehet könnyen megsejteni, ha előbb valamilyen kis N méretre konkrétan kiszámoljuk a mátrixot. Például ha N=12, akkor


Most nézzük az 511. feladatot. Erre van egy nagyon érdekes kombinatorikus bizonyítás.
Először lássunk be egy rekurziót a C mátrix elemeire. Vegyük észre, hogy ha 0 n és 0<k, akkor cn+1,k=cn,k-1+cn,k+1; ha pedig 0 n és 0<k, akkor cn+1,k=cn,k-1+cn,k+1; ha pedig 0 n, akkor cn+1,0=cn,1. Szóban ez azt jelenti, hogy a mátrixban minden elem a fölötte balra lévő és a fölötte jobbra lévő elem összege, de ha nincs fölötte balra lévő elem, akkor egyszerűen a fölötte jobbra lévő elemmel egyenlő. n, akkor cn+1,0=cn,1. Szóban ez azt jelenti, hogy a mátrixban minden elem a fölötte balra lévő és a fölötte jobbra lévő elem összege, de ha nincs fölötte balra lévő elem, akkor egyszerűen a fölötte jobbra lévő elemmel egyenlő.
Azt, hogy ez a rekurzió igaz, nem nehéz belátni, egyszerűen be kell írni a definíciót. Nézzük először az első esetet: legyen 0 n és 0<k. Ha n-k páratlan, akkor n és 0<k. Ha n-k páratlan, akkor
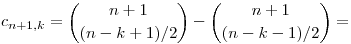
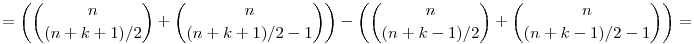
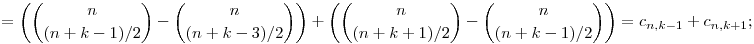
ha viszont n-k páros, akkor cn+1,k=0=cn,k-1+cn,k+1. A második esetben, ha 0 n, akkor n, akkor
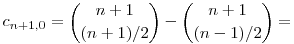
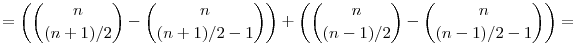
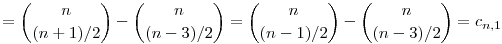
(Egy kis csalás van itt: szó szerint ennek a szabálynak a mátrix jobb szélén nincs értelme, de szerencsére tekinthetjük a mátrixot a végtelen nagy mátrix sarkának, úgyhogy igazából nincs probléma.)
Most a meglepő észrevétel az, hogy a C mátrix elemeinek kombinatorikai jelentést lehet tulajdonítani. A cn,k elem ugyanis pontosan azt számolja le, hányféleképpen lehet n lépést tenni a számegyenesen az origóból úgy, hogy minden lépésben egyet balra vagy egyet jobbra lépünk, nem lépünk rá a negatív félegyenesre, és a végén a k-ba érkezünk. Azt, hogy valóban ezt számoljuk le, nem nehéz látni a fenti rekurzió alapján.
Vegyük most szemügyre ezt a képletet, ami szerepelt a kitűzésben: ha 0 m,n akkor m,n akkor
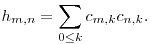
Azt állítom, hogy hm,n éppen azt számolja le, hányféleképpen lehet a számegyenesen m+n lépés hosszú sétát tenni úgy, hogy az origóból indulunk és oda is érünk vissza, minden lépésben eggyel jobbra vagy eggyel balra lépünk, és sose lépünk a negatív félegyenesre. Valóban, legyen ugyanis k az a szám, ahol az m-edik lépésben lépünk. Ekkor az első m lépés cm,k féle lehet a c fent megadott értelmezése szerint. Másrészt az utolsó n lépés éppen cn,k féle lehet, mert ha ezt az utolsó n lépést visszafele játsszuk le, akkor az origóból indulunk, és a végén érünk a k-ba. Az is látható, hogy az első m és az utolsó n lépést egymástól függetlenül választhatjuk meg akárhogyan, ha már k értékét rögzítettük, minden lehetőséghez tartozik pontosan egy m+n lépéses séta. Így megkaptuk, hogy hm,n egyenlő az m+n hosszú, origóba érkező séták számával, ami tényel m+n függvénye.
Az 513. feladatot egyelőre nem lövöm le.
|
| Előzmény: [3368] jonas, 2010-11-23 22:19:07 |
|
| [3425] m2mm | 2011-01-23 17:01:59 |
 523. feladat Egy egész együtthatós, normált polinom minden(komplex) gyökének abszolút értéke 1. Biz.: gyökei egységgyökök.
|
|
| [3424] PAL | 2011-01-21 19:48:57 |
 Kedves Tamás!
Remélem nem haragszol, hogy csatlakozom, de örömmel látom a feladatod, mert örülök annak, hogy téged is érdekelnek az efféle témák, az utóbbi hozzászólásokban kezd népszerű lenni ez a sin(nx) kifejtős téma, mely valahogy az én kedvencemmé is vált az utóbbi időben, ezért én is kiváncsian várom kitűzött feladatodra érkező megoldásokat.
|
| Előzmény: [3423] D. Tamás, 2011-01-21 19:20:26 |
|
| [3423] D. Tamás | 2011-01-21 19:20:26 |
 522.feladat: Határozzuk meg azokat a pozitív egész n számokat, melyre sin (nx) felírható sin (x) polinomjaként!
Gondolom felsőbbéveseknek közismert ez a feladat, de én nemrég találkoztam egy feladat kapcsán ezzel a gyönyörűséggel. (Persze ha valaki komoly "fegyverekkel" rendelkezik pillanatok alatt kijön a megoldás.)
|
|
|
| [3421] lorantfy | 2011-01-15 21:03:57 |
 520.feladat: Egy 24 órás, szokásos irányban járó és egy 12 órás, fordított számlapos, visszafelé járó falióra egymás mellett függenek. Mindkettő pontosan jár. A két órát egyszerre indítva nulla óráról mennyi idő múlva lesznek az órák percmutatói és óramutatói is párhuzamosak egymással és mennyi idő múlva lesznek merőlegesek egymásra?
|
 |
|
|
| [3419] Róbert Gida | 2011-01-07 17:45:06 |
 Persze, akár én is írhatnék egy ilyen programot ami úgy számolja ki, ahogy te szeretnéd. A szebb az lenne, ha már egy létező compteralgebra program is így számolná ki.
A ^ és ! műveleti sorrendje meg programfüggőnek tűnik, ahogy írtam a PARI-GP-nél és a Maple-nél például különböző.
|
| Előzmény: [3418] patba, 2011-01-07 17:21:26 |
|
| [3418] patba | 2011-01-07 17:21:26 |
 Ha mindkét program egy-egy sajátosságát(nincs multifaktoriális és hatvány nem alsóbbrendűbb, mint a faktor) felhasználva készítünk egy programot, az úgy fogja kiszámolni. Nem tudom, hogy létezik-e jelenleg ilyen program, de semmi sem zárja ki.
Viszont akkor a faktoriális, vagy a hatvány élvez előnyt műveleti sorrend szerint? Ez most már nem világos számomra.
|
| Előzmény: [3417] Róbert Gida, 2011-01-07 16:48:13 |
|
| [3417] Róbert Gida | 2011-01-07 16:48:13 |
 Igen, de nálunk több faktoriális is van, például 22!!!-et három különböző programmal néztem meg, és egyik sem adja meg a (24!)! értéket, így egyik sem számol úgy ahogy azt te szeretnéd.
A probléma hasonló ahhoz, hogy abc kifejezést hogyan értékeljük ki: ä(bc) vagy (ab)c ként.
|
| Előzmény: [3416] patba, 2011-01-07 15:28:49 |
|
| [3416] patba | 2011-01-07 15:28:49 |
 Leírtad egy hozzászólásban (jó gúnyosan), hogy a Mapple a hatványozást magasabb rendű műveletként kezeli, mint a faktoriálist, és neked csak és kizárólag egy program által igazolt összefüggés elfogadható ilyen téren.
Vagy most mire gondolsz?
|
| Előzmény: [3415] Róbert Gida, 2011-01-07 13:41:00 |
|
| [3415] Róbert Gida | 2011-01-07 13:41:00 |
 Úgy látszik, hogy a műveleti sorrend (precedencia) csak nekem fontos.
Azt azért megkérdezhetem, hogy ezt manapság nem tanítják ált. iskolákban, gimnáziumokban? +,*-ra gondolok most.
|
| Előzmény: [3407] patba, 2010-12-31 13:16:22 |
|
| [3414] djuice | 2011-01-02 00:57:23 |
 Besz@rok! :) Nem tudom elképzelni mit tököltem ezen fél órákat a felírással, hisz csak a mérleg elvet kell alkalmazni a feladat szövegének megfelelően. Mindegy, már megint bebizonyosodott, hogy mindig a bonyolultabbik oldalról közelítem a pofon egyszerű dolgokat. :)
(próbálkozva vmi ilyesmiket akartam felírni I. A-B=2; II. 2AB-B=0 persze hogy nem jó!)
Köszönöm szépen amúgy, már muszáj lesz vmi. tanárt fogadni magam mellé is. :)
|
| Előzmény: [3411] Nánási József, 2011-01-01 11:11:39 |
|
| [3413] Füge | 2011-01-01 22:09:54 |
 n 22 esetén 9n<n! ezért én is a 99!!!!!!!!-re szavazok 22 esetén 9n<n! ezért én is a 99!!!!!!!!-re szavazok
|
|
|
| [3411] Nánási József | 2011-01-01 11:11:39 |
 Ha jól értem, egyenleteket akarsz?
Legyen x fiókunk.
Akkor az első esetbe a könyvek száma y=x+2
Második esetben pedig a könyvek száma y=2x-1
Ebből jön, hogy x=3 y=5
3 fiók és 5 könyv
bocsánat ha félre értettem a kérdésed.
|
| Előzmény: [3410] djuice, 2011-01-01 01:55:15 |
|
| [3410] djuice | 2011-01-01 01:55:15 |
 Elnézést hogy ilyen gyermeteg feladvánnyal zavarok, de miközben fejben találgatva fél perc alatt rá lehet jönni a megoldásra, addig egyenletekkel felírni nekem nem sikerült az alábbi feladatot. :( (haverom 2.-os középsulis öccsének van feladva háziként!)
"Pista könyveit pakolja. Ha 1 könyvet 1 fiókba rak el, 2 könyvének már nem jut hely. Ha 1 fiókba 2 könyvet tesz, az utolsó fiókban már csak 1 könyv lesz. Hány könyve van Pistának?"
Első verzióra A-B=2 alakot tudtam felírni, de a 2. esetet sehogy sem tudjuk felírni. Igazából az érdekelne, miként kell gondolkodni a helyes felírást illetőleg?
Köszönöm!
|
|
| [3407] patba | 2010-12-31 13:16:22 |
 Igen, mert akkor a ! a kitevőbe kerül be. Ha nem a kitevőbe rakod, akkor 8!-nak kéne, hogy értelmezze. Megint oda jutottunk, ahol az előbb voltunk. Programnak ahhoz, hogy ne a kitevőben legyen, kell zárójel, kézírásban nem.
|
| Előzmény: [3403] robertgidatestvere, 2010-12-31 12:37:34 |
|
| [3406] robertgidatestvere | 2010-12-31 12:52:39 |
 Igen, de nem az volt a kérdés, hogy te mit csinálsz a gépeden, van aki beszél a számítógéphez, és egy hangfelismerő program írja a szöveget a képernyőre.
A precedencia pedig igenis fontos, számomra egy program bizonyítja egyértelműen, hogy az a precedencia amit kívánsz az tényleg igaz. 2+3*4-et egy matekprogram sem fog 20-ként kiértékelni.
|
| Előzmény: [3404] patba, 2010-12-31 12:43:32 |
|
| [3405] Tassy Gergely | 2010-12-31 12:48:41 |
 Valóban nem a programozási részére gondoltam, a 99!!!!!!!! elméletben kiszámítható ,,kézzel'' is. Persze vizsgálhatjuk azt a változatot is, ahol két !-jel nem állhat egymás mellett.
|
| Előzmény: [3404] patba, 2010-12-31 12:43:32 |
|
| [3404] patba | 2010-12-31 12:43:32 |
 Olvasd el még egyszer a feladatot!(Írni én kézzel szoktam, számítógépen meg gépelni.) Nem programozási feladat, a pontosítás szerintem csak annak szólt, hogy végtelen jelet ne használjunk, meg hasonlóakat.
Az én tippem: 99!!!!!!!!
|
| Előzmény: [3403] robertgidatestvere, 2010-12-31 12:37:34 |
|
| [3403] robertgidatestvere | 2010-12-31 12:37:34 |
 Az ötlet jó, de több probléma is van vele. Először egy olyan már létező programot kéne mutatni, amivel az adott kifejezés (elméletben) kiszámítható volna, és annyi lenne amit mondasz (plusz feltétel persze, hogy pozitív egésznek kell lennie a számnak).
Nekem már a precedencia sem világos, hogy ! vagy ^ van előrébb, bár ez programfüggőnek tűnik.
Ha PARI-GP-re gondoltál, akkor az bukta, mert a ^ jel nélkül ezt nem tudod bevinni, de egyébként sem müködne, mert itt például 2^3!=64 és nem 8!=40320. Mathematica 5.1-ben már n!!-t is multifaktoriálisként értelmezi, így ez már itt elbukik. Maple 12-ben rákérdez n!! esetén, hogy dupla faktoriálist kérsz, vagy a faktoriálist kétszer alkalmazva. De n!!! esetén nekem soha nem alkalmazza a faktoriálist háromszor. Így ez is bukta.
|
| Előzmény: [3402] patba, 2010-12-31 11:44:39 |
|
|
|
| [3400] Tassy Gergely | 2010-12-30 23:29:00 |
 519. feladat. Melyik a 10 karakterrel leírható legnagyobb pozitív egész szám?
(A feladat további pontosításra szorul, egyelőre csak gondolatébresztőnek szántam. Karakter alatt elsősorban a számjegyeket, az alapműveleti jeleket, valamint szükség esetén további, egy számítógép-billentyűzeten megtalálható betűket, szimbólumokat (pl. e, !) értek. Várom az esetleges további felmerülő kérdéseket, ötleteket.)
|
|
|
| [3398] ibiro | 2010-12-29 22:20:00 |
 Tényleg jó az oldal, kösz szépen. Amit ott láttam nem matematikai megoldás, tehát akit érdekel érdemes valami matematikai megoldást is keresni.
|
| Előzmény: [3397] Tóbi, 2010-12-29 01:37:14 |
|
| [3397] Tóbi | 2010-12-29 01:37:14 |
 Kiszámítottam az első pár tagot, arra rákerestem, ezen az oldalon, ahol a nevezetes egész sorozatokat tartják számon. Itt van minden hivatkozás a sorozattal kapcsolatban, utána lehet nézni, ha érdekel. Egyébként valóban csak az első 43 tag egész, utána egyik sem az. Szerintem nagyon hasznos a fenti adatbázis, sokat segített volna a Kömalban is, de sajnos csak az egyetemen hallottam róla először.
|
| Előzmény: [3396] ibiro, 2010-12-28 23:03:29 |
|
|
|
|
| [3393] jonas | 2010-12-10 19:27:40 |
 Az 511-re lényegében jó a válaszod, de csak akkor ez a képlet, ha m+n páros, különben hm,n=0.
Az 512-re jó a válaszod, a tanulság pedig az, hogy ha csak az 511-re adott képletet látnád, akkor sokkal nehezebb lenne megkapni a determinánst, mint így.
Az 513-ra vagy nem egészen jó a megoldásod, vagy a feladatot adtam fel rosszul, mert nem csupa nullák vannak a szorzatban.
|
| Előzmény: [3392] stray dog, 2010-12-10 13:13:34 |
|
|
|
| [3390] apci | 2010-12-09 21:22:52 |
 Sziasztok! Ezzel a feladattal nem boldogulok:
|
 |
|
| [3389] Tóbi | 2010-12-07 22:25:50 |
 Először is egy átfordítás nem hozhat létre kört, és amíg nincs kör, mindig lesz átfordítható csúcs. Tehát a folyamat végtelen sokáig fog tartani. Azt kellene igazolni, hogy minden csúcs végtelen sokszor átfordul. Ekkor Mariska néni eljuthat K-ból A-ba: kinéz egy tetszőleges irányítatlan K-A utat, és átmegy az egyes éleken, mikor azok a megfelelő irányba fordulnak. Tekintsünk egy minimális csúcsszámú gráfot, ahol az állítás nem igaz. Tegyük fel, hogy P olyan csúcs, ami csak véges sokszor fordul át. Ekkor egy idő után P már nem forog, és a P-ből kimenő élek száma monoton nő. Egy idő után ez is megáll. Hasonló igaz a P-ből elérhető pontokra, majd az azokból elérhetőekre is stb. Az elérhető csúcsok halmaza legyen S. Ha V(G)=S akkor egy idő után nem lenne több átfordulás, ez kizárt. Tehát néhány pont kimarad, egy idő után ezek közt zajlana minden átfordulás, mégpedig az S-el nem szomszédosak közt. Tekintsük most a V(G)\S csúcsai által adott részgráfot, és legyen ebben P' egy S-sel szomszédos pont (ilyen létezik az összefüggőség miatt). Ez egy kisebb ellenpélda lenne az állításra.
|
| Előzmény: [3385] Fálesz Mihály, 2010-12-07 12:48:40 |
|
|
|
| [3386] Sirpi | 2010-12-07 13:20:04 |
 Nagyon jó a megfogalmazás :-)
Csak lehet, hogy valamit félreértek, mert túl könnyűnek tűnik ellenpéldát gyártani:
Legyen 3 város, A, B és C, és a kezdeti kétirányú (összefüggő) úthálózat álljon az AB és BC utakból (Mariska néni A-ban lakik, C-be akar eljutni). A kezdeti irányítás legyen C->B->A, ez Mariska néninek nyilván nem fog tetszeni. Erre CB-t megfordítják: C<-B->A, de ekkor B lesz forrás, így CB-t megint megfordítják: C->B->A s.í.t., Mariska néni pedig hoppon marad (persze ha másodszor nem CB-t, hanem BA-t fordítjuk meg, akkor meg is van a kívánt út, szóval meg lehet oldani, hogy eljusson, de azt is, hogy ne).
Ja, és ez nem csak 3 városra ellenpélda, mert nyilván ha B-be becsatlakozik még egy csomó másik út, mondjuk mind B-ből kifelé, akkor is ugyanezt el lehet mondani).
|
| Előzmény: [3385] Fálesz Mihály, 2010-12-07 12:48:40 |
|
| [3385] Fálesz Mihály | 2010-12-07 12:48:40 |
 516. feladat (Valamikor réges-régen, egy nem annyira távoli galaxisban, olimpiai előkészítőn volt.)
Bergengóciában olyan az úthálózat, hogy a városok közötti utak nem ágaznak el, minden út két várost köt össze. Az úthálózat összefüggő, vagyis az utakon bármelyik városból bármelyik városba el lehetett jutni --- legalábbis a múlt hétig. A világgazdasági válság miatt ugyanis a bergengóc kormány változatos megszorításokra kényszerült. Az Utazásról Leszoktató Minisztérium például a következőket rendelte el:
56789/2010. Min. rendelet a helyváltoztatás szabadságának megőrzéséről és védelméről
1.§ (a) Az ország mindegyik útját egyirányúsítani kell.
(b) Az utak irányítását olyan módon kell megválasztani, hogy ne lehessen körbe utazni több város között.
Az intézkedés bevezetése ellen hevesen tiltakoztak a kukutyiniak, mert hozzájuk minden út befelé vezetett, és emiatt sehova nem tudtak utazni. A demonstráció vezérszónoka Mariska néni volt, aki az unokahúga nagybátya sógorának a régi kollégiumi szobatárását szerette volna meglátogatni Alsómocsoládon. A tiltakozások eredményeként a minisztérium a következővel egészítette ki a rendeletet:
2.§ (a) Minden héten, ha van olyan város, ahonnan csak kifelé vezet út, akkor ezek közül ki kell választani az egyiket, és az innen kifelé vezető utak irányítását meg kell fordítani.
(b) Az (a) pont rendelkezéseiben előírtaktól eltekintve, a többi út irányítása nem változik.
Eljuthat-e Mariska néni Kukutyinból Alsómocsoládra?
|
|
| [3384] Tóbi | 2010-12-01 02:43:46 |
 Tényleg van explicit megoldás. Ha k lehetséges végkimenetel van, a idegen egymástól függetlenül a szelvényt vesz, mi pedig k darabot, akkor a nyereményünk várható összege  jelöléssel: jelöléssel:
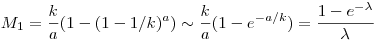
ha különböző szelvényeket veszünk,
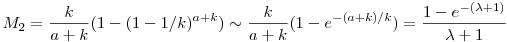
ha véletlenszerűen töltjük ki a szelvényeket.
|
| Előzmény: [3383] Róbert Gida, 2010-11-30 21:22:46 |
|
|
| [3382] Róbert Gida | 2010-11-30 21:20:15 |
 Itt szerintem neked feltételes valószínűséget kéne számolnod, ha összesen k darab telitalálat volt, akkor mennyi a valószínűsége, hogy ebből nekünk n darab telitalálatunk volt (persze 0 n n k). Amit te csinálsz a második szummában sehol nem jelenik meg k a valószínűségben, mást számolsz. k). Amit te csinálsz a második szummában sehol nem jelenik meg k a valószínűségben, mást számolsz.
Az, hogy rossz, legkönnyebben úgy látod: b=k azaz, ha minden szelvény telitalálatos, ekkor persze csak az lehet, hogy az összes szelvényünk nyert, ami a te formuládból nem következik.
Egyszerűbb egyébként úgy számolni, hogy k1 darab telitalálat volt a 8 millió szelvényből, és k2 darab volt nekünk (dupla szumma lesz itt is). Tóbi megoldása mindenesetre szellemesebb és rövidebb.
|
| Előzmény: [3381] Füge, 2010-11-30 18:12:07 |
|
| [3381] Füge | 2010-11-30 18:12:07 |
 Tóbi, a második részben te csak azt az esetet nézed, mikor egy szelvénnyel nyerünk nem? A véletlen miatt többel is nyerhetünk egyszerre, ilyenkor meg nagyobb részét kapjuk meg a nyereménynek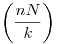 .Róbert Gida elmondanád kicsit részletesebben, hogy mi nem jó az én képletemben, mert nem igazán értem. Adott k érték esetén kiszámolom a nyereményem várható értékét, ezeket beszorzom a valószínűséggel, majd összegzem. Legalább is ezt akartam leírni. .Róbert Gida elmondanád kicsit részletesebben, hogy mi nem jó az én képletemben, mert nem igazán értem. Adott k érték esetén kiszámolom a nyereményem várható értékét, ezeket beszorzom a valószínűséggel, majd összegzem. Legalább is ezt akartam leírni.
|
|
|
| [3379] Tóbi | 2010-11-30 01:08:15 |
 Legyen 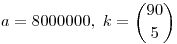 , a nyeremény 1. Az első esetet Füge már jól kiszámolta: , a nyeremény 1. Az első esetet Füge már jól kiszámolta:
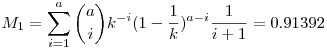
A 2. estben k szelvény van, mindegyik 1/k eséllyel nyer, így a nyeremény várható értéke egyenlő egy biztosan nyerő szelvény várható értékével. Ez az előzőek szerint számolható, csak a helyett a+k-1 további szelvény rontja az esélyeinket.
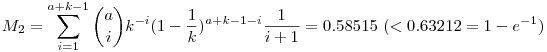
Az összegeket Maple-lel számoltam ki, i=100-ig.
|
| Előzmény: [3376] Róbert Gida, 2010-11-29 15:39:04 |
|
| [3378] Róbert Gida | 2010-11-29 22:43:33 |
 A második nem jó: b-ből kiválasztod a telitalálatosokat, aztán pedig a 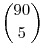 szelvényből a telitalálatosokat. szelvényből a telitalálatosokat.
Amúgy, ha csak közelítő eredmények érdeklik az embert, akkor elég elmenni addig, hogy legfeljebb mondjuk 100 telitalálat volt (már 100-nak is roppant kicsi az esély), továbbá nem racionális számokkal számolni, hanem lebegőpontossal, ha nem akarunk több millió jegyű számokkal szórakozni.
|
| Előzmény: [3377] Füge, 2010-11-29 20:23:06 |
|
| [3377] Füge | 2010-11-29 20:23:06 |
 Ha mindegyik szelvényt különbözően töltjük ki akkor biztosan 1 szelvénnyel fogunk nyerni, tehát a nyereményünk csak attól függ, hogy a többi szelvényből hány db nyert. Legyen a nyeremény: N, i db 5ös találat a 8.000.000 szelvényből és az egyszerűség kedvéért 8.000.000=a
![M_1=\sum_{i=0}^a\left[\binom{a}{i}\left[\frac{1}{\binom{90}{5}}\right]^i\left[1-\frac{1}{\binom{90}{5}}\right]^{(a-i)}\frac{N}{i+1}\right]](keplet.cgi?k=4E3895F80F12B0BC)
A második részt két változóval írtam fel, összesen k db telitalálat, ebből n db a miénk. 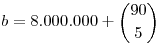
![M_2=\sum_{k=1}^b\left[\binom{b}{k}\left[\frac{1}{\binom{90}{5}}\right]^k\left[1-\frac{1}{\binom{90}{5}}\right]^{b-k}\sum_{n=0}^k\left[\binom{\binom{90}{5}}{n}\left[\frac{1}{\binom{90}{5}}\right]^n\left[1-\frac{1}{\binom{90}{5}}\right]^{\binom{90}{5}-n}\frac{nN}{k}\right]\right]](keplet.cgi?k=95E55BE97EE39516)
Gondolom, erre lehetne írni egy programot, ami szépen kiszámolja, de sajnos én nem tudok. Remélem, hogy jó, mert megszenvedtem a TeX-szel mire beírtam :)
|
|
| [3376] Róbert Gida | 2010-11-29 15:39:04 |
 A példa amúgy az idei Ankéton szerepelt: http://www.komal.hu/hirek/anket/2010/program2010.h.shtml Juhász István előadása.
Ez viszont már saját:
515. feladat Tegyük fel, hogy amikor már sokan játszanak a nagy nyereményért 8 millió szelvény érkezik be egy héten átlagosan. Mi történik, ha csak mi beszállunk és beküldünk 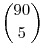 szelvényt. Mikor nagyobb a várható nyereményünk és mennyi (csak az ötös nyereményosztályban), ha véletlenszerűen töltjük ki a szelvényeket, vagy, ha mindegyiket különbözően? szelvényt. Mikor nagyobb a várható nyereményünk és mennyi (csak az ötös nyereményosztályban), ha véletlenszerűen töltjük ki a szelvényeket, vagy, ha mindegyiket különbözően?
(Csak egy hétig játszunk. Lottónál egy adott nyereményosztályban mindenki ugyanannyit kap.)
|
| Előzmény: [3371] Füge, 2010-11-28 19:55:48 |
|
|
|
|
|
|
| [3370] Róbert Gida | 2010-11-28 16:59:50 |
 514. feladat Véletlenszerűen kitöltünk 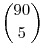 db ötöslottó szelvényt. Mennyi a valószínűsége, hogy lesz legalább egy öttalálatosunk? db ötöslottó szelvényt. Mennyi a valószínűsége, hogy lesz legalább egy öttalálatosunk?
|
|
| [3369] stray dog | 2010-11-26 16:18:14 |
 Köszönöm szépen!
Amúgy anno kihoztam hogy ha létezik vmelyik n-re ellenpélda, akkor minden m>n-re sem lehet igaz az állítás. Jelen esetben n=5, így minden 5-nél nagyobb értékre már nem teljesül az egyenlőtlenség.
|
| Előzmény: [3367] Tóbi, 2010-11-23 21:44:13 |
|
| [3368] jonas | 2010-11-23 22:19:07 |
 Ez a feladatcsokor a kedvencem, gonosz módon föladva. Ha így nehéz, kérhettek segítséget, mert tudok olyat mondani, ami még nem lő le mindent.
Legyen bármely n,k nemnegatív egészre ha n és k paritása azonos, akkor
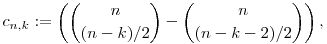
ha viszont n és k paritása különböző, akkor cn,k:=0. Épüljön fel a C négyzetes mátrix ezekből az elemekből, vagyis valamilyen N méretre legyen

Legyen H=CCT, azaz a H mátrix elemei
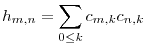
511. feladat Lássuk be, hogy a H visszafele csíkozott, azaz hm,n függvénye m-n-nek. Például h7,5=h8,4=h9,3=132.
512. feladat Mennyi H determinánsa?
Legyen bármely n,k nemnegatív egészre Un(x) az x-nek az az n-edfokú polinomja, amire Un(cos  )=sin ((n+1) )=sin ((n+1) )/sin )/sin  (ezeket másodfajú Csebisev-polinomnak hívják), és legyen un,k az xk együtthatója ebben a polinomban. Képezzük az un,k számokból is egy N méretű négyzetes U mátrixot. (ezeket másodfajú Csebisev-polinomnak hívják), és legyen un,k az xk együtthatója ebben a polinomban. Képezzük az un,k számokból is egy N méretű négyzetes U mátrixot.
513. feladat Számítsuk ki a CU szorzatot.
|
|
| [3367] Tóbi | 2010-11-23 21:44:13 |
 Ez pontosan az egyik kedvenc feladatom, pár éve magamtól vetettem fel, és hosszú agyalás után sikerült megoldani. Egy kis segítség a megoldáshoz:
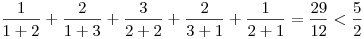
Próbálj ellenpéldát találni minden n 5-re és bizonyítani n=3,4-re. Végül határozd meg a kifejezés lehetséges legkisebb értékét (infimum). (Itt nem írok végeredményt, hadd gondolkodjon más is.) 5-re és bizonyítani n=3,4-re. Végül határozd meg a kifejezés lehetséges legkisebb értékét (infimum). (Itt nem írok végeredményt, hadd gondolkodjon más is.)
|
| Előzmény: [3365] stray dog, 2010-11-23 12:56:09 |
|
| [3366] D. Tamás | 2010-11-23 18:11:41 |
 n=3 esetén pont a Nesbitt-egyenlőtlenséget kapjuk, ami nevezetes. Egyébként a feladat igazolható a Titu-lemmával és a Számtani-mértani közepek közötti egyenlőtlenség felhasználásával.
|
| Előzmény: [3365] stray dog, 2010-11-23 12:56:09 |
|
| [3365] stray dog | 2010-11-23 12:56:09 |
 Sziasztok!
Igazából nem tudom hogy ebbe a topicba való-e, de ezt találtam a megfelelőbbnek. Szóval anno még középiskolásként a következő feladattal találkoztam:
Igaz-e, hogy ha x1,x2,...,xn tetsz. poz. valós számok, és n 3, akkor mindig fennáll a köv. egyenlőtlenség: 3, akkor mindig fennáll a köv. egyenlőtlenség:
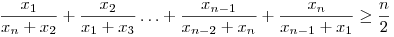
Az igazsághoz hozzátartozik még, hogy akkor nem tudtam megoldani. Most, hoszzú évek után, ismét kedvet kaptam egy kis matekozáshoz, de sajnos már nem rendelkezem a megfelelő ismerettel. Így a segítségeteket kérem. Az is jó, ha vki már látta a feladatot, és megadja, hogy hol érdemes utánanézni. Nekem úgy rémlik hogy a The American Mathematical Monthly-ban szerepelt még nagyon régen (60-as évek?), és akkor még mint megoldatlan probléma. Előre is köszönöm a segítséget! :)
|
|
|
|
| [3362] Róbert Gida | 2010-11-17 20:59:02 |
 Ez így elég pongyola. Nem indokoltad, hogy miért is lehet egy végtelen szorzatot csak úgy lecserélni. Négyzetre emeléssel hamis gyök is bejöhetett. De akár megoldást is elveszíthettél. Ha Kömal javító lennék simán kerek nulla pontot adnék egy ilyen megoldásra.
|
| Előzmény: [3360] nadorp, 2010-11-17 15:42:56 |
|
|
|
|
|
|
|
|
| [3353] Sirpi | 2010-11-07 20:44:48 |
 Nem engem kérdeztetek, de azért reagálok. A feladat valószínűleg nem bennem merült fel először, de nem olvastam sehol, magamtól találtam ki, hogy meg kellene oldani. És nekem is ugyanez jött ki megoldásnak, hozzátéve, hogy rengeteg más számláló is passzol a 9091-es nevezőhöz.
|
| Előzmény: [3352] vogel, 2010-11-07 20:37:05 |
|
| [3352] vogel | 2010-11-07 20:37:05 |
 Szerintem leprogramozta. Ezt nem is nagyon lehet máshogy. Vagy igen??
|
|
| [3351] HoA | 2010-11-07 19:58:13 |
 Ismerted a feladatot, sőt közismertnek tartottad - mint már annyiszor - és ezért koppintottál ránk az eredmény számszerű közlésével vagy megoldottad de lusta voltál leírni a megoldást?
|
| Előzmény: [3350] Róbert Gida, 2010-11-06 23:17:36 |
|
|
| [3349] Sirpi | 2010-11-06 20:45:48 |
 510. feladat: egy racionális számot normálisnak nevezünk, ha a tizedestört-alakjában egy periódusban mind a 10 számjegy ugyanannyiszor fordul elő (pl. 0,(2468013579)(2468013579)...).
Melyik a legkisebb pozitív egész nevező, melyhez van olyan számláló, hogy a számlálót a nevezővel elosztva a kapott hányados normális szám?
|
|
| [3348] m2mm | 2010-11-02 19:40:49 |
 509. feladat
Vegyünk egy (p-1)x(p-1)-es négyzetet, ahol p prím. Bontsuk fel 1x1-es négyzetekre, úgy, hogy a négyzetek oldalai párhuzamosak a nagy négyzet oldalaival.
Biz. ki lehet választani p (négyzet)csúcsot, hogy ne legyen köztük 3 egy egyenesre eső.
|
|
|
| [3346] DF | 2010-10-24 20:42:10 |
 Sziasztok! A következő feladat matematikai modelljét szeretnénk felépiteni. Adott két síkbeli egyenes, e1 és e2. Hajlásszögük fi. Bárhová helyezzünk el egymástól 2a távolságra 2db érzékelőt a síkon. Keressük az e1 egyenesen a1(t), v1(t); e2 egyenesen az e1 egyenesen mozgóval egyirányban illetve ellentétes irányban a2(t); v2(t) gyorsulással illetve pillanatnyi sebességgel mozgó anyagi pontok minimális távolságát megadó képletet. Egy matematikus mérnök azt javasolta, hogy térjünk át bipoláris koordináta rendszerbe. Például a metszéspontja e1 e2 egyeneseknek egy pont u,v paraméterrel, amik valójában szögek. Ezzel a ponttal az érzékelők polár egyenese adott a pályához képest. Ezekkel az adatokkal a szenzorok távolságától függően is adódik a keresett minimális távolság képlet. Ezzel pedig az egyébként azonos érzékelők tulajdonságát tudjuk figyelembe venni. Szeretnénk a minimális távolságot adó képletet meghatározni bipoláris koordináta rendszerben. (A korábbi számításunk csak derékszögű koordináta rendszerre vonatkozott. És nem vettük figyelembe a szenzorokat. Sajnos csak úgy tudtuk megoldani és csak derékszögű kereszteződésre. A bipoláris koordináta rendszerről pedig még nem hallottunk, nemhogy számolni tudnánk benne. Mások pedig lehülyézték a mérnököt, hogy halandzsázik. Tudomásul vette és távozott.)
|
|
|
| [3344] Róbert Gida | 2010-10-11 13:26:35 |
 Az már más kérdés, hogy a Maple isprime funkciója nem valódi prímtesztet ad (így kicsit megtévesztő is a fv. neve). A Maple help menüjéből:
"The isprime command is a probabilistic primality testing routine."
|
| Előzmény: [3343] Sirpi, 2010-10-11 12:34:04 |
|
| [3343] Sirpi | 2010-10-11 12:34:04 |
 Köszi, valóban ezekre gondoltam és én is pont így kerestem meg őket. Mondjuk 24-jegyű számra is lehet gyors prímtesztet írni, de az már nem megy, hogy a gyökéig végignézzük, hogy van-e osztója. Olyan 18-19 jegynél kezdett bedögleni ez a hozzáállás. De utána maple-ben megírtam az egészet, használva az isPrime beépített funkciót, és a 24-jegyű megoldás is meglett percen belül.
Viszont tuti, hogy nem az I.4-ből jött az ötlet, mert annak megjelenésekor már épp nem jártam egyetemre :-)
|
| Előzmény: [3342] jonas, 2010-10-11 12:16:09 |
|
| [3342] jonas | 2010-10-11 12:16:09 |
 Ha jól értelmezem a definíciódat, akkor ezek a right-truncatable prímek és left-truncatable prímek. Valóban meg lehet keresni az összeset, mégpedig úgy, hogy a kevesebb számjegyűekhez hozzápróbálsz minden számjegyet az elejére vagy a végére, majd ellenőrzöd, hogy prím-e. Az egyikből a leghosszabb is csak 8 számjegyű, ezeket itt a KöMaLon az I. 4. feladatból ismerheted, annak idején e miatt én is megkerestem az összeset. A másikból a leghosszabb kb. 24 számjegyű, és összesen néhány ezer van belőle, tehát ahhoz, hogy ebből megtaláld az összeset, legfeljebb néhány tízezer (legfeljebb 25 jegyű) számot kell prímtesztelni (felbontani nem kell), ez pedig nem tarthat sok ideig.
|
| Előzmény: [3341] Sirpi, 2010-10-11 11:39:44 |
|
| [3341] Sirpi | 2010-10-11 11:39:44 |
 Nem néztem utána, hogy létezik-e erre hivatalos definíció (majd valaki megmondja), de még egyetem alatt kitaláltam az "elölről prím/hátulról prím" fogalmakat. Ezek olyan prímek, hogy bárhol kettévágjuk őket, a vágás előtti/utáni részük is prím. Sikerült is megtalálnom mindkét fajtából mindet (szóval mindkettőből véges sok van). Ám az egyiknél még működött is, hogy minden számot a négyzetgyökéig teszteltem, hogy prím-e, de a másiknál ez a módszer csődöt mondott, miután 20-jegyű számokat kellett vizsgálnom, de végül megoldottam. Ha valakinek van kedve, megkeresheti ezeket a számokat.
|
| Előzmény: [3338] Lóczi Lajos, 2010-10-11 03:02:49 |
|
|
|
| [3338] Lóczi Lajos | 2010-10-11 03:02:49 |
 Egy prímet ciklikusnak nevezünk, ha számjegyeinek ciklikus permutációi mind prímek; más szóval, ha első számjegyét a végére téve ismét olyan prímet kapunk, amelyik ciklikus.
Például a 197 ciklikus prím, mert 197, 971 és 719 mind pímek.
Melyik az egymillió alatti legnagyobb ciklikus prím?
|
|
|
|
| [3335] Tóbi | 2010-10-02 22:38:44 |
 Igazad, van rossz következtetést vontam le abból, hogy van körbeverés. Ez csak azt jelenti, hogy a lehetséges kockák nem állíthatók sorba erősség szerint. Ettől még lehetne olyan kocka, ami minden másikat szigorúan legyőz.
|
| Előzmény: [3334] Csimby, 2010-10-02 22:00:45 |
|
| [3334] Csimby | 2010-10-02 22:00:45 |
 Pont te bizonyítottad be, hogy a szabályos kocka legerősebb, abban az értelemben, hogy senki se veri őt (a 21 összegű kockák közül). Persze ettől még igazad van, hogy másik 3 kocka körbeverheti egymást (de a szabályos kocka nem lehet benne ilyen körbeverésben).
Az A kocka legyen nagyobb a B kockánál, akkor, ha az Ai-Bj értékek között több pozitív van, mint negatív. Ez a reláció nem lesz tranzitív mint ahogy azt az előbb te is írtad, viszont maximális elemei lehetnek (akiknél mindenki akivel összehasonlítható, kisebb vagy egyenlő - jelen esetben persze mindenki mindenkivel összehasonlítható). A szabályos kocka pl. maximális.
|
| Előzmény: [3333] Tóbi, 2010-10-02 21:36:54 |
|
| [3333] Tóbi | 2010-10-02 21:36:54 |
 Nem lehet egyértelműen meghatározott legerősebb kocka. Ugyanis A=(4,4,4,4,4,1) B=(6,6,6,1,1,1) C=(6,3,3,3,3,3,) esetén A veri C-t 25-11-re, C veri B-t 18-15-re, és B veri A-t 18-15-re. Így (bármilyen számhalmazból kerüljenek is ki a felírt számok) kevert stratégiát kell használni, ha egyszerre kell megadnunk az egész kockánkat. Az eredeti feladatra ez persze nem ad választ, de indokolja, hogy mi értelme van egyesével számozni a kockákat.
|
| Előzmény: [3332] Csimby, 2010-10-02 21:03:32 |
|
| [3332] Csimby | 2010-10-02 21:03:32 |
 Hoa: Ez jó ötlet volt, köszi (valójában az kell, hogy Ni-Si-k között több legyen a pozitív mint negatív, nem az, hogy 18-nál több legyen)
Tóbi: Igen, ez jó. Kivéve ha 6-nál nagyobb számok is lehetnek a másik kockán (ami nem volt megtiltva). De a győzelmek száma ekkor se mehet 15 fölé, míg a döntetlenek száma ekkor is legfeljebb 6.
És ha 21 helyett valamimásik C 6 poz. egész a számok összege? Igaz lenne hogy az ilyen kockák között mindig vannak legerősebbek? 6 poz. egész a számok összege? Igaz lenne hogy az ilyen kockák között mindig vannak legerősebbek?
És ha nem pozitív egészeket is írhatunk a lapokra (nyilván bármilyen fix alsó korlát nem jelentene lényeges különbséget)?
|
| Előzmény: [3331] Tóbi, 2010-10-02 20:31:32 |
|
| [3331] Tóbi | 2010-10-02 20:31:32 |
 A szabályos (1,2,3,4,5,6) kocka ellen bármilyen (a,b,c,d,e,f) kocka 15 esetben nyer, 15 esetben veszít 6 döntetlen mellett, ha a+b+c+d+e+f=21. Ugyanis ha a 2. kockával a-t dobunk, akkor a szabályos kocka válaszai közül a-1 db győzelmet, 1 db döntetlent eredményez nekünk. Így 6 döntetlen lesz, és a-1+b-1+c-1+d-1+e-1+f-1=21-6=15 esetben nyerünk és 6*6-15-6=15 esetben veszítünk.
|
| Előzmény: [3329] HoA, 2010-10-02 20:00:58 |
|
|
| [3329] HoA | 2010-10-02 20:00:58 |
 Először azt kéne megnézni, van-e jobb kocka a "szabályos"-nál? Mert ha nem, akkor A akármilyen számokat is ír, B-nek szabályos ( 1,2,3,4,5,6 ) kockát kell készítenie. Az N nemszabályos kocka akkor jobb az S szabályosnál, ha a kockákra írt számok 36 darab Ni-Sj ( i,j = 1,2,...,6 ) különbségből 18-nál több pozitív.
Ha van jobb kocka, akkor igazi a feladat: A jobb kockájánál tud-e B mégjobbat készíteni?
|
| Előzmény: [3328] Csimby, 2010-10-02 19:46:13 |
|
|
|
| [3326] Csimby | 2010-10-02 18:08:47 |
 508. feladat
A és B a következőt játsszák: mindkettőjüknek van egy dobókockája, számok nélkül. Először A ír egy pozitív egész számot a saját kockájának az egyik lapjára, majd B tesz ugyanígy. Ezután megint A ír egy pozitív egész számot a saját kockájának egyik lapjára, majd B stb. Amire vigyázniuk kell, hogy a számok összege egyik kockán sem lehet nagyobb mint 21. Mikor már minden lapon szerepel szám, dobnak a saját kockájukkal és az nyer, aki nagyobb számot dobott a másiknál.
Kinek milyen stratégiával érdemes játszani?
(Az igazság az, hogy nem tudom milyen nehéz feladat, csak eszembe jutott.)
|
|
|
|
|
| [3322] HoA | 2010-09-30 13:10:20 |
 Tekintsük a feltételezett X megoldást szintén ciklikus felírásban. Mivel az 5 X3-ra helyben marad, ezért ő vagy egyelemű, vagy hárommal osztható hosszúságú ciklus tagja. Összesen 5 elem van, tehát ez csak hármas ciklus lehet. Ugyanez igaz a 4-re. Így a lehetőségek:
a) 5 is, 4 is egyelemű ciklus
b) 5 egyelemű, 4 egy hármas ciklus tagja
c) 4 egyelemű, 5 egy hármas ciklus tagja
d) 4 is és 5 is hármas ciklus tagja
A b) és c) eset könnyen kizárható, ekkor ugyanis a maradék egy elem is egyelemű ciklust alkot, tehát X3 –ra helyben maradna A d) esetben, mivel 5 elemből legfeljebb egy hármas ciklus képezhető, 4 és 5 ugyanannak a ciklusnak a tagjai, de ekkor ennek a ciklusnak a harmadik tagja is helyben maradna X3-ra. Marad az a) eset, az útmutatás tkp. erre vonatkozik. 4 és 5 nem mozog, tehát csak az 1 2 3 elemekkel kell foglalkoznunk. Van-e olyan permutációjuk, melynek harmadik hatványa (1 2 3) ? Esetszétválasztással elvben a lehetőségek:
d1) 3 egyelemű ciklus – nem jó, X3-ra helyben maradnak
d2) 1 egyelemű és 1 kételemű ciklus – nem jó, az egyelemű ciklus tagja helyben marad
d3) 1 háromelemű ciklus – nem jó, ennek harmadik hatványa mindhárom elemet helyben hagyja.
|
| Előzmény: [3309] epsilon, 2010-09-26 13:28:39 |
|
| [3321] epsilon | 2010-09-27 05:34:43 |
 Nagyon valószínű a magyarítás, mert pl. a transzpoziciót is a Wikipédia is elemcserének, a ciklust ciklikus permutációnak, stb. nevezi, tehát magyarítás nyugodtan lehet.
|
| Előzmény: [3320] jonas, 2010-09-26 22:31:21 |
|
|
| [3319] epsilon | 2010-09-26 20:55:20 |
 Igen Mihály, ezt értem, ez az előző hozzászólásod "láncsorának" a magyarázata, Én is felírtam a többi ugyanolyan "láncsort" amit az előbbi hozzászólásodban írtál, így bejön összesen 10 betű. Ezen felírások által sem látom, hogy mi lenne az ellentmondás, ami miatt nem létezik az x permutáció.
|
| Előzmény: [3318] Fálesz Mihály, 2010-09-26 20:32:10 |
|
| [3318] Fálesz Mihály | 2010-09-26 20:32:10 |
 Az x egy {1,2,3,4,5} {1,2,3,45} permutáció, amit keresel. Ez az 1-et elviszi valamilyen a elembe, az a-t elviszi valamilyen b-be, b-t pedig 2-be és így tovább. {1,2,3,45} permutáció, amit keresel. Ez az 1-et elviszi valamilyen a elembe, az a-t elviszi valamilyen b-be, b-t pedig 2-be és így tovább.
|
| Előzmény: [3314] epsilon, 2010-09-26 19:02:29 |
|
| [3317] epsilon | 2010-09-26 19:26:08 |
 Kedves Miháy! Noha a második vázlat érdekesnek tűnik, és nem tudtam követni, mindemellett az "Ha x3 harmadrendű, akkor az x hányadrendű?" kérdésed alapján összeállt egy megoldás, ami a következő: x a 9-ik hatványon éppen az identikus permutációt adja. És ekkor nem nehéz igazolni, hogy a 9-nek osztania kellene az 5!=1×2×3×4×5-öt, és ez absurdum, ígyhát nem létezik az x. Mindemellett, ha van rá türelmed, nagyon örvendenék annak a másik megoldásnak amit vázlatoltál. Tisztelettel üdv: epsilon
|
| Előzmény: [3311] Fálesz Mihály, 2010-09-26 14:47:33 |
|
|
|
| [3314] epsilon | 2010-09-26 19:02:29 |
 Kedves Mihály! Köszi szépen az útmutatást! Van benne számomra néhány megtévesztő dolog: az "elem pályája" az csak személyes megfogalmazás, vagy szakkifejezés? A "9 elem" honnan annyi, mert Én az x permutációban ha ismeretlennek tekintenénk akkor az 1,2,3,4,5 alatt a,b,c,d,e mindössze 5 betűre lenne szükség és nem 9-re. A nálad bejött a-f hat betű miket jelöl? Az x×x×x permutáció szorzásából? Szóval ha tudnád részletezni, előre is megköszönném! Üdv: epsilon
|
| Előzmény: [3313] Fálesz Mihály, 2010-09-26 17:25:07 |
|
|
| [3312] epsilon | 2010-09-26 16:22:25 |
 Szeretném kikerülni az elem rendjére vonatkozó ismereteket, csak a permutáció és a ciklusokra vonatkozóan szeretném megoldani, vajon így lehetséges-e? Mert a diákok akiknek szól nem tanultak csoportelméletet.
|
| Előzmény: [3311] Fálesz Mihály, 2010-09-26 14:47:33 |
|
|
| [3309] epsilon | 2010-09-26 13:28:39 |
 Üdv Mindenkinek! Egy középiskolás feladat a következő: igazoljuk, hogy az X×X×X=(2 3 1)(4)(5) ciklusszorzattal (ciklikus permutációkkal) adott permutáció egyenletnek nincs megoldása az S(5)-ben (az 5-öd rendű permutációk halmazán). Útmutatásnak ennyi szerepel: "Egy permutáció 3 hatványra emelésével nem kaphatunk egyetlen 3 hosszúságú ciklust." Elemi módszerrel nem tudom belátni ezt, vagyis a kért egyenlet megoldását. Valaki tudna-e segíteni? Előre is köszönöm!
|
|
| [3308] Lóczi Lajos | 2010-09-26 13:28:12 |
 Van-e olyan f:R R bijekció, amelyre f(0)=0, f folytonos a 0-ban, de az inverze nem folytonos a 0-ban? R bijekció, amelyre f(0)=0, f folytonos a 0-ban, de az inverze nem folytonos a 0-ban?
|
|
|
| [3306] Kristóf Miklós 2 | 2010-08-28 11:27:22 |
 Kedves Mindenki, egy feladvány a latin négyzetekkel kapcsolatban: .
.
.
.
acb
cba
bac
ez egy latin négyzet. Legyen ez egy szorzótábla!
Ekkor ez ezt tudja:
x*x = x idempotencia (x*y)*z = (x*z)*(y*z) jobbdisztributivitás x*(y*z) = (x*y)*(x*z) baldisztributivitás
négyre is van ilyen:
acdb
dbac
bdca
cabd
Kérdés: Tudtok ilyet 5-re, 6-ra, n-re?
Ezt úgy hívják, hogy DILA, azaz Disztributív, Idempotens, Latin Algebra.
|
|
| [3305] Sirpi | 2010-08-24 11:07:51 |
 ...kivéve, ha q=3 a második esetnél (hogy teljes legyen a bizonyítás). Valamint az összeg párosnál, és 3-mal oszthatónál nem árt megnézni, hogy nem lehet se 2, se 3 (de ez trivi).
|
| Előzmény: [3304] jenei.attila, 2010-08-24 09:18:03 |
|
|
| [3303] D. Tamás | 2010-08-23 10:43:49 |
 Mutassuk meg, hogy ha p és q prímszámok, akkor a pq+qp összeg csak egyetlenegy esetben prímszám, ha p=2 és q=3. (p<q) A feladat egyáltalán nem nehéz, ezt most előre leszögezem.
|
|
| [3302] Róbert Gida | 2010-08-18 17:38:34 |
 Nem azt mondtam, hogy nehéz a megoldása, hanem azt, hogy gyenge a feladatkitűzés.
Amúgy Tóbi megoldása még mindig rossz, azt nem tudom miért tette fel, hogy xi>0 amikor a feladatban természetes egészekről van szó. És ekkor van pontosan egy megoldás, (ha minden xi különböző és n 2): 0!+1!=2!. 2): 0!+1!=2!.
|
| Előzmény: [3298] D. Tamás, 2010-08-17 21:07:40 |
|
| [3301] Tóbi | 2010-08-18 16:00:25 |
 Így sem nehéz a megoldás. Állítás: Ha n 2 rögzített egész, akkor n db faktoriális összege csak véges sok esetben lehet faktoriális. Bizonyítás: Tegyük fel, hogy a legnagyobb tag az összegben (jelölje k!) nagyobb, mint n!. Ekkor az n tag összege k! és (k+1)! közé esik, hiszen n*k!<k*k!<(k+1)!. Véges sok eset kivételével lesz is ilyen nagy a tagok közt. Egyébként valószínűleg tényleg így gondolták eredetileg a feladatot, ez indokolja a "csak véges sok megoldás"-t a szövegben. 2 rögzített egész, akkor n db faktoriális összege csak véges sok esetben lehet faktoriális. Bizonyítás: Tegyük fel, hogy a legnagyobb tag az összegben (jelölje k!) nagyobb, mint n!. Ekkor az n tag összege k! és (k+1)! közé esik, hiszen n*k!<k*k!<(k+1)!. Véges sok eset kivételével lesz is ilyen nagy a tagok közt. Egyébként valószínűleg tényleg így gondolták eredetileg a feladatot, ez indokolja a "csak véges sok megoldás"-t a szövegben.
|
| Előzmény: [3300] Fálesz Mihály, 2010-08-18 13:44:20 |
|
|
|
|
|
|
|
|
|
|
|
| [3290] Sirpi | 2010-07-16 13:35:21 |
 Szerintem elég egyszerűen kijön, hogy ha 0 t t 1, akkor ha a, b, c oldalakból szerkeszthető háromszög, akkor az at, bt, ct oldalakból is, egyéb t értékekre pedig van ellenpélda. 1, akkor ha a, b, c oldalakból szerkeszthető háromszög, akkor az at, bt, ct oldalakból is, egyéb t értékekre pedig van ellenpélda.
Ha 0 t t 1, akkor a 1, akkor a b b c-ből következik, hogy at c-ből következik, hogy at bt bt ct, ezért elég megmutatni, hogy c<a+b-ből következik, hogy ct<at+bt. Mivel c<a+b, így ezt leosztva c1-t-vel: ct, ezért elég megmutatni, hogy c<a+b-ből következik, hogy ct<at+bt. Mivel c<a+b, így ezt leosztva c1-t-vel:
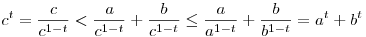
tehát valóban ct<at+bt.
Ha t>1, akkor elég kis epszilonra az 1,1,2- oldalú háromszög megfelelő, viszont az 1t,1t,(2- oldalú háromszög megfelelő, viszont az 1t,1t,(2- )t-re már nem teljesül a háromszög-egyenlőtlenség, mert (2- )t-re már nem teljesül a háromszög-egyenlőtlenség, mert (2- )t>2. )t>2.
Amúgy a t<0 is hasonlóan érdekes eset, arra is van egyszerű ellenpélda (ha  elég kicsi, akkor elég kicsi, akkor  ,1,1 megfelelő háromszög, de ,1,1 megfelelő háromszög, de  t>2). t>2).
|
| Előzmény: [3286] D. Tamás, 2010-07-15 16:05:08 |
|
| [3289] D. Tamás | 2010-07-16 12:19:24 |
 Ha minden igaz, megvan a felső korlát: n 1 Most csupán eredményt közlök, levezetni sem olyan nehéz, mint gondoltam. Azonban az alsó korlát megkeresése már nehezebb lesz úgy vélem. (Legalábbis bizonyítani biztosan az lesz, ha megsejtettük a számot.) 1 Most csupán eredményt közlök, levezetni sem olyan nehéz, mint gondoltam. Azonban az alsó korlát megkeresése már nehezebb lesz úgy vélem. (Legalábbis bizonyítani biztosan az lesz, ha megsejtettük a számot.)
|
|
| [3288] D. Tamás | 2010-07-16 11:45:46 |
 A 2 feladat hasonló, de nem ugyanaz.
B. 3936. Milyen feltételeknek kell teljesülni az a,b,c valós számokra ahhoz, hogy minden n természetes számra létezzék olyan háromszög, amelynek az oldalai an,bn és cn?
Az én feladatom pediog a következő volt: Igaz-e, hogy ha a,b és c oldalakból szerkeszthető (sík)háromszög, akkor an,bn és a cn oldalakból is szerkeszthető háromszög, ha n R\R-? Ez könnyen elmondható, hogy nem igaz, hiszen példának vehetjük a 3 4 és 5 egység hosszúságú oldalakkal rendelkező háromszöget. Ez a példa azért is speciális, mert n=2 esetén megkapjuk az oldalak közti összefüggést: 32+42=52 (De egyébként R\R-? Ez könnyen elmondható, hogy nem igaz, hiszen példának vehetjük a 3 4 és 5 egység hosszúságú oldalakkal rendelkező háromszöget. Ez a példa azért is speciális, mert n=2 esetén megkapjuk az oldalak közti összefüggést: 32+42=52 (De egyébként  pithagoraszi számhármasnál ezt tapasztalhatjuk. Összefoglalva ez a feladat azért más a B.3936-hoz képest, mert itt meg kell keresnünk azokat az n számokat, melyekre igaz lesz, hogy az an,bn és cn hosszúságú szakaszokl szerkeszthető háromszög. n=1 és pithagoraszi számhármasnál ezt tapasztalhatjuk. Összefoglalva ez a feladat azért más a B.3936-hoz képest, mert itt meg kell keresnünk azokat az n számokat, melyekre igaz lesz, hogy az an,bn és cn hosszúságú szakaszokl szerkeszthető háromszög. n=1 és  jó eset, de ez nem zárja ki a többi eset létezését. Mivel a probléma egyre jobban érdekel, ezért én is nekiállok a feladatnak mostantól. Bár van egy olyan sejtésem, hogy ez nem egy egyszerű probléma, na de majd meglátjuk. jó eset, de ez nem zárja ki a többi eset létezését. Mivel a probléma egyre jobban érdekel, ezért én is nekiállok a feladatnak mostantól. Bár van egy olyan sejtésem, hogy ez nem egy egyszerű probléma, na de majd meglátjuk.
|
| Előzmény: [3287] psbalint, 2010-07-15 16:52:31 |
|
|
| [3286] D. Tamás | 2010-07-15 16:05:08 |
 Teljesen általánosan is felvetődhet a kérdés: Tehát ha a,b és c oldalakból szerkeszthető (sík)háromszög, akkor an,bn és a cn oldalakból is szerkeszthető háromszög, ha n R\R-.? A válasz nem, de jó feladatnak tűnik - elsőre - megkeresni az n lehetséges értékeit. R\R-.? A válasz nem, de jó feladatnak tűnik - elsőre - megkeresni az n lehetséges értékeit.
|
|
|
|
|
| [3282] Kós Géza | 2010-07-11 20:17:08 |
 Az idei matekolimpián az 5. feladat volt a legérdekesebb, szerintem érdemes itt is megbeszélni.
506. feladat (IMO2010/5). A B1,B2,B3,B4,B5,B6 dobozok mindegyikében kezdetben egy érme van. Kétféle megengedett lépés van:
1. típusú lépés: Választunk egy Bj nemüres dobozt, ahol 1 j j 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz. 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz.
2. típusú lépés: Választunk egy Bk nemüres dobozt, ahol 1 k k 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával. 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával.
Állapítsuk meg, hogy ilyen lépések valamilyen véges sorozata segítségével elérhető-e, hogy a B1, B2, B3, B4, B5 dobozok mindegyike üres legyen, a B6 doboz pedig pontosan 201020102010 érmét tartalmazzon. (Definíció szerint abc=a(bc).)
|
|
| [3281] jonas | 2010-05-12 23:13:41 |
 gabor7987 feladata a Valaki monja meg! téma 1024. hozzászólásában annyira megtetszett, hogy föladtam egy nehezebb változatát az idei BME matematika versenyen. A feladat így szól.
505. feladat. Adott két 1-nél nagyobb egész szám: m és n. Bizonyítsuk be, hogy csak véges sok n-edik hatvány áll elő mn egymás utáni egész szám n-edik hatványának az összegeként.
Próbáljátok meg megoldani. Köszönet gabor7987-nak az ötletért, jenei.attilának a megoldás ötletéért, valamint Horváth Miklósnak amiért évek óta fáradhatatlanul szervezi a versenyt.
|
|
| [3280] HoA | 2010-04-30 10:42:01 |
 Tájékozódásul vizsgáljuk a felület metszetét sorra az x=0, y=0, x=y , x= -y síkokkal. A kapott függvények:
f1=y4–y2=y2(y2–1) zérushelyei -1, 0, 1 , a függvény jellegét az origó környezetében az 1. ábra mutatja. Tehát ebben az irányban itt lokális maximum van.
f2=x4–x2=x2(x2–1) hasonló f1 -hez.
f3 : Legyen x=y=t . f3=2t4–4t2=2t2(t2–2) jellegében megegyezik az előzőekkel, csak a zérushelyek itt (  ) )
f4 : Legyen x= -y = t . f4=2t4–2t2+2t2=2t4 A metszetgörbe jellege a 2. ábra szerinti, ebben az irányban lokális minimum van. A felületnek tehát az origó nyeregpontja. Általánosabb eredményt kapunk, ha áttérünk polárkoordinátákra. x=rcos ,y=rsin ,y=rsin helyettesítéssel helyettesítéssel
g(r, )=r4(cos4 )=r4(cos4 +sin4 +sin4 )–r2(cos )–r2(cos +sin +sin )2 Az r szerinti deriváltak az origóban )2 Az r szerinti deriváltak az origóban 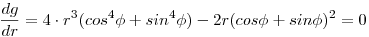 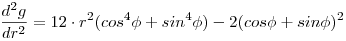 Ez általában negatív és az 1. ábra szerinti viselkedést indokolja. A kivétel éppen az x = -y eset, ekkor a második tag eltünik, és így még a harmadik derivált is nulla. A negyedik derivált pozitív volta adja a 2. ábra szerinti metszetet. Összefoglalásként megállapíthatjuk, hogy az origó ennek a függvénynek egy különleges nyeregpontja, egy irányban lokális minimum, az összes többiben lokális maximum. Ez általában negatív és az 1. ábra szerinti viselkedést indokolja. A kivétel éppen az x = -y eset, ekkor a második tag eltünik, és így még a harmadik derivált is nulla. A negyedik derivált pozitív volta adja a 2. ábra szerinti metszetet. Összefoglalásként megállapíthatjuk, hogy az origó ennek a függvénynek egy különleges nyeregpontja, egy irányban lokális minimum, az összes többiben lokális maximum.
Hátha valaki folytatja e,césv vektorok elemzésével.
|
 |
| Előzmény: [3279] Lóczi Lajos, 2010-04-23 23:34:25 |
|
| [3279] Lóczi Lajos | 2010-04-23 23:34:25 |
 (Szélsőérték szempontjából) milyen típusú pontja az f(x,y):=x4-x2-2xy+y4-y2 felületnek az origó?
|
|
| [3278] HoA | 2010-04-23 17:38:03 |
 Gondolatébresztőnek kezdjük az általános esettel, a térkép hasonlatnál maradva legyen az origó felett közönséges domboldal. Ekkor a szintvonal két irányába mutat v1=v0 és v2=-v0 és ezekre merőleges a gradiens, e=g és c=-g . ( A minusz jelek nálam nem igazán jól látszanak. ) Érdekesebbek a speciális terepalakulatok - csúcs , nyereg, töbör .
|
| Előzmény: [3277] Lóczi Lajos, 2010-04-17 14:04:34 |
|
| [3277] Lóczi Lajos | 2010-04-17 14:04:34 |
 A térbeli x-y-z koordinátarendszerben tekintsünk egy sima "domborzati térképet" az x-y alapsík fölött, azaz legyen adott egy f:R2 R deriválható függvény. Tekintsük az alapsíkban az összes origó kezdőpontú egységvektort, és jelöljük meg ezek közül mindazokat az e, c és v vektorokat, amelyek irányában az f felület origó fölötti f(0) pontjában rendre: legmeredekebb az emelkedés, legnagyobb a csökkenés, illetve a pontbeli adott irányú érintőegyenes vízszintes. R deriválható függvény. Tekintsük az alapsíkban az összes origó kezdőpontú egységvektort, és jelöljük meg ezek közül mindazokat az e, c és v vektorokat, amelyek irányában az f felület origó fölötti f(0) pontjában rendre: legmeredekebb az emelkedés, legnagyobb a csökkenés, illetve a pontbeli adott irányú érintőegyenes vízszintes.
Milyen összefüggések állapíthatók meg az e, c és v vektorok között?
|
|
| [3276] Tóbi | 2010-04-14 15:35:35 |
 Vegyük az egyenlőtlenség logaritmusát. k*log(a)=<L*log(b)<k*log(a)+log(2) Tulajdonképpen itt log(b) olyan többszörösét keressük, amit maradékosan osztva log(a)-val, a maradék legfeljebb log(2) lesz. Amennyiben log(a)/log(b) racionális a maradék 0 is lehet, ha irracionális, tetszőlegesen megközelíti a 0-t, így log(2) alá is megy.
|
| Előzmény: [3272] m2mm, 2010-04-13 23:21:09 |
|
|
|
|
| [3272] m2mm | 2010-04-13 23:21:09 |
 Igaz-e, hogyha a>b>1 a és b valós, akkor létezik pozitív egész k,l, hogy ak<bl<2ak?
|
|
|
|
|
|
|
|
| [3265] Lóczi Lajos | 2010-03-25 22:55:31 |
 Legyen a>0 adott valós szám. Mi lesz n  esetén az esetén az
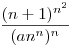
sorozat határértéke?
|
|
|
|
| [3262] Alma | 2010-02-25 17:12:18 |
 Szerintem függ, hogy melyik az az adott elem k-as. Vegyük például azt a leegyszerűsített esetet, hogy a kockának két oldala van: 1,2 és n=3szor dobunk.
Azok a számsorok, melyekben az 11 elemkettes pontosan egyszer fordul elő: 112 és 211.
Azok a számsorok, melyekben a 12 elemkettes pontosan egyszer fordul elő: 112, 121, 122, 212.
A két eseménynek nem egyenlő a valószínűsége.
|
| Előzmény: [3261] Láda19, 2010-02-25 16:21:43 |
|
| [3261] Láda19 | 2010-02-25 16:21:43 |
 Lenne egy valószínűségszámítási probléma, amit a napokban kérdeztek tőlem, de még nem tudtam megoldani. Szeretném, ha valaki segítene.
Egy dobókockával n-szer dobunk, majd a dobások eredményét leírjuk egymás mellé. Mennyi a valószínűsége annak, hogy az 1, 2, 3, 4, 5, 6 számokból képezett, adott elem k-as (k<n) pontosan egyszer előfordul az n hosszúságú számsorban?
|
|
|
|
| [3258] Fálesz Mihály | 2010-02-19 12:41:32 |
 Számomra inkább az érdekes, hogy ezzel a módszerrel primitív gyökök felhasználása nélkül is ilyen röviden be lehet bizonyítani azt, hogy a akkor és csak akkor kvadradikus maradék mod p, ha a(p-1)/2 1(mod p), különben a(p-1)/2 1(mod p), különben a(p-1)/2 -1. -1.
(A kis Fermat-tétel párosítgatás és Wilson-tétel nélkül is kijön a szokásos bizonyítással: összeszorozzuk az a,2a,...,(p-1)a maradékokat.)
|
| Előzmény: [3256] bily71, 2010-02-17 23:30:28 |
|
| [3257] bily71 | 2010-02-18 21:45:01 |
 Én arra jutottam, hogy a le nem fedett számok halmaza végtelen. Gondoltmenetem a következő:
Vonjuk össze az egy modulushoz tartozó számtani sorozatokat, így minden 3-nál nagyobb prímhez kapunk egy olyan számsorozatot, amelyben két differencia váltja egymást. Írjuk fel a sorokat egymás után képzeletben. A sorok táblázatba rendezhetőek, a táblázatban a számok a prímek szorzata egyhatodának alsó, vagy felső egészrészének felelnek meg. Ezt a táblázatot azt hiszem már jól ismerjük.
Ha a le nem fedett számok halmaza véges lenne, akkor létezne k természetes szám, hogy e szám nem, de minden nála nagyobb fedett. Ez csak úgy lehetséges, ha minden új sorozat legkisebb olyan tagja, amely eddig egyik sorozatnak sem volt tagja fedi a k után következő olyan számot, amelyet az előző sorozatok nem fedtek le, (remélem eddig érthetően fogalmaztam).
Jelölje an az n-edik le nem fedett számot, bn pedig az n-edik sorozat azon legkisebb tagját, amely nem szerepelt egyik eddigi sorozatban sem. Mivel a táblázat a főátlóra szimmetrikus, ezért ![a_n<\left[\frac{p_n^2}{6}\right]\le{b_n}](keplet.cgi?k=27E2DD7917EF967E) , ebből következik, hogy an<bn, így soha nem fedheti, mert az an=bn soha nem teljesül. , ebből következik, hogy an<bn, így soha nem fedheti, mert az an=bn soha nem teljesül.
Jól következtettem? Eléggé tömören fogalmaztam, ha nem érthető, bővebben kifejtem.
A nem fedett számok egy nevezetes számsorozat tagjaival egyértelműen megfeleltethetőek .
|
| Előzmény: [3253] bily71, 2010-02-16 20:04:32 |
|
| [3256] bily71 | 2010-02-17 23:30:28 |
 Két eset lehetséges:
1. a nem kvadratikus maradék modulo p. Ekkor a Wilson-tétel miatt
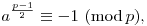
ebből
ap-1 1 (mod p), 1 (mod p),
ebből
ap a (mod p). a (mod p).
2. a kvadratikus maradék modulo p. Ekkor a Wilson-tétel miatt
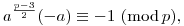
ebből

ebből ugyancsak a kis Fermat-tételt kapjuk.
(Az előző megoldásom második része részben hibás).
|
| Előzmény: [3252] Fálesz Mihály, 2010-02-15 10:16:52 |
|
| [3255] jonas | 2010-02-16 20:54:36 |
 Nem, én azt állítom, hogy a következő egy lefedő rendszer:
x0 0(mod p0) 0(mod p0)
x1 1(mod p1) 1(mod p1)
x2 -1(mod p2) -1(mod p2)
x3 2(mod p3) 2(mod p3)
x4 -2(mod p4) -2(mod p4)
x5 3(mod p5) 3(mod p5)
stb, ahol pi mondjuk a prímszámok sorozata.
Ez akkor is működik, ha mondjuk pi=10i+1: ilyenkor a kongruenciák közül bármelyik véges sok együtt csak a természetes számok legfeljebb egy kilenced részét fedi le, mégis az összes kongruencia együtt már lefedi az összes egész számot.
|
| Előzmény: [3248] bily71, 2010-02-14 23:10:38 |
|
|
| [3253] bily71 | 2010-02-16 20:04:32 |
 Ez a kongruenciarendszer minden természetes számot lefed a 0-án kívül, tehát részleges lefedőrendszer. Változtassunk egy kicsit a szabályokon. Legyen az ![x_n\equiv\left[\frac{p_n}{6}\right]~(\mod{p_n})](keplet.cgi?k=9446EE673F8A0723) kongruenciáknak megfelelő számtani sorozatok első eleme kongruenciáknak megfelelő számtani sorozatok első eleme ![p_n+\left[\frac{p_n}{6}\right]](keplet.cgi?k=6C0902C528816160) , az , az ![x_m\equiv-\left[\frac{p_m}{6}\right]~(\mod{p_m})](keplet.cgi?k=F051519F148EC06D) kongruenciáknak megfelelőeknek pedig változatlanul kongruenciáknak megfelelőeknek pedig változatlanul ![-\left[\frac{p_m}{6}\right]](keplet.cgi?k=728CDC07E3F05BB2) . .
Nevezzük az ilyen rendszereket, ahol a kongruenciáknak megfelelő számok sorozata nem a maradékosztályt reprezentáló legkisebb elemtől indul, számtani sorozatok lefedőrendszerének, ha minden természetes szám tagja legalább egy sorozatnak. Számtani sorozatok részleges lefedőrendszerének pedig akkor, ha létezik k>0 természetes szám, úgy, hogy a rendszer minden k-nál nagyobb számot lefed.
Utolsó kérdésem e témában: 1. Az így kapott számtani sorozatok rendszere részleges lefedőrendszer-e, vagyis a le nem fedett számok halmaza véges, avagy végtelen?
Mégegyszer elnézést kérek a témakör érdektelenségéért.
|
| Előzmény: [3248] bily71, 2010-02-14 23:10:38 |
|
|
| [3251] Fálesz Mihály | 2010-02-15 10:16:11 |
 Én pontosan fordítva szervezném a számolást:
1. eset: a -1 nem kvadradikus maradék mod p, azaz minden pár két különböző maradékból áll. A párok száma (p-1)/2. A Wilson-tételt is alkalmazva,
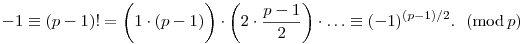 | (1) |
Mivel p>2, a +1 és -1 maradékok különbözőek, a -1 (-1)(p-1)/2 (mod p) kongruencia akkor teljesül, ha (p-1)/2 páratlan, azaz p 4k+3 alakú. (-1)(p-1)/2 (mod p) kongruencia akkor teljesül, ha (p-1)/2 páratlan, azaz p 4k+3 alakú.
2. eset: a -1 kvadradikus maradék mod p, azaz létezik egy a maradék, amire a2 -1(mod p). Ilyen maradék a -a is, a két maradék külöböző, mert p páratlan, és több nincs. -1(mod p). Ilyen maradék a -a is, a két maradék külöböző, mert p páratlan, és több nincs.
Az (1)-beli szorzatból hagyjuk el a (a,a) és a (-a,-a) párokat, és helyettük vegyük hozzá a szorzathoz az (a,-a) párt (ahol a.(-a)=-a2 +1(mod p)): +1(mod p)):
-1 (p-1)!=(a.(-a)).(1.(p-1)).... (p-1)!=(a.(-a)).(1.(p-1)).... (-1)(p-3)/2. (mod p) (-1)(p-3)/2. (mod p) | (2) |
A -1 (-1)(p-3)/2 (mod p) kongruencia akkor teljesül, ha (p-3)/2 páratlan, azaz p 4k+1 alakú. (-1)(p-3)/2 (mod p) kongruencia akkor teljesül, ha (p-3)/2 páratlan, azaz p 4k+1 alakú.
Összességében az derült ki, hogy a -1 akkor és csak akkor kvadradikus maradék mod p, ha p 4k+1 alakú.
|
| Előzmény: [3250] bily71, 2010-02-14 23:27:08 |
|
|
|
| [3248] bily71 | 2010-02-14 23:10:38 |
 Tehát, ha jól értem azt állítod, hogy az
x1 m(mod p1) m(mod p1)
x2 m(mod p2) m(mod p2)
...
xn m(mod pn) m(mod pn)
végtelen kongruenciarendszer lefedőrendszer?
Szerintem nem.
Bármelyik számot fedem le az összes kongruenciával, az ugyanaz, mintha a 0-át fedném le. Az eratoszthenészi szita működik akkor is, ha nem a 0-ról indítjuk a lépéseket, hanem m-ről, hiszen minden modulus prím, csak ebben az esetben nem a pl. 5-tel osztható számokat húzzuk le, hanem m-től minden 5k-adik számot.
Ha pedig arra gondoltál, hogy minden kongruenciával másik számot fedünk le, azt egy esetként írtam le, vagyis a végtelen sok megoldást egy típusba soroltam.
De mi a helyzet akkor, ha minden 3-nál nagyobb prímet kétszer használunk fel, és ha a lefedett szám függ a modulustól, mint a következő rendszerben:
x1 1(mod 5) 1(mod 5)
x2 -1(mod 5) -1(mod 5)
x3 1(mod 7) 1(mod 7)
x4 -1(mod 7) -1(mod 7)
x5 2(mod 11) 2(mod 11)
...
](keplet.cgi?k=31B7602D9EBE3CC4)
,](keplet.cgi?k=65AD1F2195D695B8)
ahol ha pn=6k+1, akkor ![\left[\frac{p_n}{6}\right]](keplet.cgi?k=EC986CB74BE95A64) az alsó egészrészt jelöli, ha pn=6k-1, akkor pedig a felsőt? Lehet-e ez a rendszer részleges lefedőrendszer, tehát létezik-e olyan természetes szám, hogy minden nála nagyobbat lefed a rendszer? az alsó egészrészt jelöli, ha pn=6k-1, akkor pedig a felsőt? Lehet-e ez a rendszer részleges lefedőrendszer, tehát létezik-e olyan természetes szám, hogy minden nála nagyobbat lefed a rendszer?
|
| Előzmény: [3246] jonas, 2010-02-14 17:18:58 |
|
| [3247] bily71 | 2010-02-14 22:12:36 |
 Ezt kapjuk:
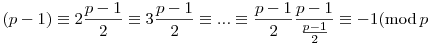
.
Két eset lehetséges, első:
2 |  , ekkor van , ekkor van  darab számpárunk, amelyek szorzata ab darab számpárunk, amelyek szorzata ab -1(mod p), ha behelyettesítünk, akkor ezt kapjuk: -1(mod p), ha behelyettesítünk, akkor ezt kapjuk:

.
Második:
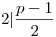 , ekkor létezik a, hogy a2 , ekkor létezik a, hogy a2 -1(mod p), de akkor (p-1)2 -1(mod p), de akkor (p-1)2 -1(mod p). Így kapunk -1(mod p). Így kapunk  darab számpárt, amelyek szorzata ab darab számpárt, amelyek szorzata ab -1(mod p), és mivel 2 -1(mod p), és mivel 2 |  , ezért, ha behelyettesítünk, ezt kapjuk: , ezért, ha behelyettesítünk, ezt kapjuk:

.
|
| Előzmény: [3243] Fálesz Mihály, 2010-02-13 12:38:17 |
|
| [3246] jonas | 2010-02-14 17:18:58 |
 Ne viccelj már. Ha végtelen sok kongruenciát használhatsz, és csak a modulusokra van megkötés, akkor nagyon sok megoldás van, mert akár minden kongruenciával elég egy egész számot lefedned.
|
| Előzmény: [3244] bily71, 2010-02-13 12:46:49 |
|
|
| [3244] bily71 | 2010-02-13 12:46:49 |
 Triviális megoldás az
x1 1(mod p1) 1(mod p1)
x2 2(mod p2) 2(mod p2)
...
xn n(mod pn), n(mod pn),
kongruenciarendszer, ahol n végig fut a természetes számokon, pn>n és a prímek páronkét különböznek.
A p1<p2<...<pn nem szükséges feltétel, pn itt nem az n-edik prímet jelöli és nem szükséges minden prímet felhasználni, akár végtelen sok is kimaradhat.
Egy másik:
x1 a1(mod p1) a1(mod p1)
x2 a2(mod p2) a2(mod p2)
x3 a3(mod p3) a3(mod p3)
...
xm am(mod pm) am(mod pm)
xm+1 b1(mod pm+1) b1(mod pm+1)
...
xm+n bn(mod pm+n), bn(mod pm+n),
ahol bi pi valamely maradékosztálya, bi és bj nem feltétlenül különböző számok, bn<pm+n és bn az n-edik olyan természetes szám, amely nem elégít ki p1-től pm-ig egy kongruenciát sem, pm nem az m-edik prím és p1<p2<...<pm+n itt sem szükséges feltétel, és itt sem szükséges minden prímet felhasználni.
1. Van-e több megoldás?
(Szerintem nincs a jonas által [3239]-ben ismertetett okok miatt.)
Nevezzünk részleges lefedőrendszernek egy olyan kongruenciarendszert, ahol létezik k természetes szám, hogy a k-nál nagyobb természetes számok mindegyike kielégít valamely kongruenciát, azaz k fölött a rendszer minden számot lefed.
2. Konstruálható-e véges, vagy végtelen részleges inkongruens lefedőrendszer, ha minden modulus prím?
3. Konstruálható-e véges, vagy végtelen részleges lefedőrendszer, ha minden modulus prím, és minden prímet kétszer használunk fel?
Elnézést, ha bárkit is untatok.
|
| Előzmény: [3241] bily71, 2010-02-12 22:53:59 |
|
|
|
|
|
| [3239] jonas | 2010-02-12 21:57:23 |
 Nyilván nem, mert a modulusok relatív prímek, így mindegyik sorozat tagjaihoz egyet hozzáadva a kapott sorozatoknak van metszetük, és az ebben lévő számok egyik eredeti sorozatban sincs benne.
|
| Előzmény: [3238] bily71, 2010-02-12 21:01:37 |
|
| [3238] bily71 | 2010-02-12 21:01:37 |
 Konstruálható-e inkongruens lefedőrendszer csak prím modulusú tagokból?
|
|
|
|
| [3235] Sirpi | 2010-02-11 18:03:18 |
 m2mm úgy érti, hogy a bizonyítás ilyen hosszúságban elmondható (gyakorlatilag változatlan formában) úgy, hogy nem ejted ki azt a szót, hogy latin négyzet. Mellesleg én is ezt a bizonyítást ismerem a tétel "alap" bizonyításának.
|
| Előzmény: [3234] bily71, 2010-02-11 17:28:19 |
|
| [3234] bily71 | 2010-02-11 17:28:19 |
 Annyi köze van a latin négyzetekhez, hogy ha nem latin négyzetekről lenne szó, akkor nem biztos, hogy tudnánk párokat képezni, ugyanis nem lenne biztosított, hogy minden sorban szerepeljen az egyes, főleg, hogy csak egyszer, biztosítva a párok egyértelműségét, elvégre definíció szerint egy n×n-es latin négyzet az 1-től n-ig terjedő egész számokat tartalmazza úgy, hogy minden sorában és oszlopában egy szám csak egyszer szerepel.
|
| Előzmény: [3233] m2mm, 2010-02-11 14:52:08 |
|
| [3233] m2mm | 2010-02-11 14:52:08 |
 Ez korrekt megoldás, de ennek valójában semmi köze a latin négyzetekhez. Egyszerűen párokat képezel, ez az egyik legismertebb bizonyítása a tételnek.
|
| Előzmény: [3231] bily71, 2010-02-11 12:49:08 |
|
|
| [3231] bily71 | 2010-02-11 12:49:08 |
 Ha életedben nem hallottad, hogy a latin négyzetek segítségével a Wilson-tétel bizonyítható, ez bizonyára érdekes lesz számodra, és legalább nem "halál ismert", legalábbis általad, (itt most az idézőjel nem iróniát, hanem tényleges idézést jelöl).
Legyen p P, azaz prím. Képezzünk p maradékosztályaiból, a 0-át kihagyva szorzótáblát. Ekkor a táblázat latin négyzet, ezt már [3187]-ben beláttuk. P, azaz prím. Képezzünk p maradékosztályaiból, a 0-át kihagyva szorzótáblát. Ekkor a táblázat latin négyzet, ezt már [3187]-ben beláttuk.
Ennek az a következménye, hogy minden a-hoz létezik egy, és csakis egy b szám, hogy
ab 1(mod p), 1(mod p),
ahol a és b p egy-egy maradékosztálya.
Az a=b csak a=1, vagy a=p-1 esetén fordulhat elő, minden más esetben a b, ugyanis, ha b, ugyanis, ha
a2 1(mod p), 1(mod p),
akkor
a2-1 0(mod p), 0(mod p),
de akkor p nem lehet prím, mert
a2-1=(a-1)(a+1) 0(mod p). 0(mod p).
Ennek az a következménye, hogy az 1<a<p-1 maradékosztályok párokba rendezhetőek, így lesz 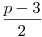 darab olyan számpárunk, hogy darab olyan számpárunk, hogy
aibj 1(mod p). 1(mod p).
Ezeket a számpárokat helyettesíthetjük 1-gyel, így a következőt kapjuk:
(p-1)!=1.2.3...(p-3)(p-2)(p-1)=1.1...1.1(p-1) p-1(mod p). p-1(mod p).
Q.E.D.
|
| Előzmény: [3186] Róbert Gida, 2010-02-01 17:11:09 |
|
|





 0, akkor
0, akkor 

 k. A k=0 esetre egyszerűen un+1,k=un-1,k. Ez egyszerűen abból következik, hogy a másodfajú Csebisev-polinomokra igaz a következő rekurzió.
k. A k=0 esetre egyszerűen un+1,k=un-1,k. Ez egyszerűen abból következik, hogy a másodfajú Csebisev-polinomokra igaz a következő rekurzió.  -t. (Hogy így esetleg nem minden x kapható meg, az lényegtelen, mert mindkét oldal polinom, tehát elég csak egy intervallumon belátni, hogy egyenlők.) Szorozzuk meg mindkét oldalt sin
-t. (Hogy így esetleg nem minden x kapható meg, az lényegtelen, mert mindkét oldal polinom, tehát elég csak egy intervallumon belátni, hogy egyenlők.) Szorozzuk meg mindkét oldalt sin  +
+ )=sin
)=sin 
 >0 szám, hogy a függvény leszűkítése a [-
>0 szám, hogy a függvény leszűkítése a [-


 22 esetén 9n<n! ezért én is a 99!!!!!!!!-re szavazok
22 esetén 9n<n! ezért én is a 99!!!!!!!!-re szavazok


 n
n N.
N. 



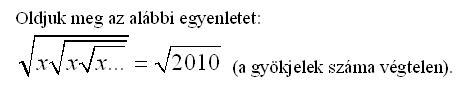




 {1,2,3,45} permutáció, amit keresel. Ez az 1-et elviszi valamilyen a elembe, az a-t elviszi valamilyen b-be, b-t pedig 2-be és így tovább.
{1,2,3,45} permutáció, amit keresel. Ez az 1-et elviszi valamilyen a elembe, az a-t elviszi valamilyen b-be, b-t pedig 2-be és így tovább.  a
a
 oldalú háromszög megfelelő, viszont az 1t,1t,(2-
oldalú háromszög megfelelő, viszont az 1t,1t,(2-

 ,y=rsin
,y=rsin


 ha a<e, 1 ha a=e és 0 ha a>e.
ha a<e, 1 ha a=e és 0 ha a>e.
 x3 (mod p), ha pedig p=3k+1, a akkor, és csak akkor kubikus maradék, ha a(p-1)/3
x3 (mod p), ha pedig p=3k+1, a akkor, és csak akkor kubikus maradék, ha a(p-1)/3