| [3849] w | 2014-02-28 21:14:28 |
 Jó megoldás, de nem kell ide feltétlenül multiplikatív inverz. Talán elemibb megoldás, amit találtam és tálaltam:
1. Tegyük fel, hogy van olyan (n,a,b) hármas, melyre nem igaz, és vegyük a legkisebb ilyen n-et! Ha ekkor a és n rendelkezik közös prímosztóval, akkor ez a prímosztó b-t is osztja, így leosztva vele (n,a,b)-t, kisebb, de megfelelő számhármashoz jutunk. Tehát n és a relatív prím.
2. Márpedig n|a100+b100 és n|a104+b104, ezért
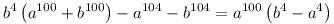
osztható vele, ahonnan a relatív prímek miatt a4 b4 (mod n). Ezt pedig visszahatványozva adódik, hogy n|a100+b100 b4 (mod n). Ezt pedig visszahatványozva adódik, hogy n|a100+b100 2a100. Ebből megint relatív prímek miatt következik, hogy n|2. Ami pedig ellentmondás, hisz n=1 és n=2-re triviális az állítás. 2a100. Ebből megint relatív prímek miatt következik, hogy n|2. Ami pedig ellentmondás, hisz n=1 és n=2-re triviális az állítás.
|
| Előzmény: [3848] csábos, 2014-02-28 00:08:20 |
|
|
| [3847] w | 2014-02-27 22:33:18 |
 Köszönöm, hogy ezeket így felsoroltad. Érdekes és egyszerű sorozatnak tűnik, az OEIS-ben mégsem találtam meg.
Bizonyítsuk be számológép nélkül, hogy a 101 és 111 is a sorozat tagja lesz!
|
| Előzmény: [3846] Róbert Gida, 2014-02-27 21:54:09 |
|
| [3846] Róbert Gida | 2014-02-27 21:54:09 |
 Hozzászóláskorlát nem engedi meg, hogy felsoroljam a számokat, de ezer alatt ezen számok (és többszörösei) a megfelelőek, elsőre hihetetlen soknak tűnik, de valójában nem véletlen, hiszen csupán 1022 darab 10-csökkenő (pozitív) szám van. A kérdést egyébként teljesen meg lehet válaszolni, mert az 1022 darab szám osztói közül kerülnek ki azon számok melyeknek van 10-csökkenő többesük, és pontosan 6178 darab ilyen szám van.
[11, 100, 101, 111, 156, 221, 223, 232, 249, 261, 267, 299, 348, 369, 384, 387, 439, 441, 447, 457, 463, 467, 469, 497, 501, 503, 507, 512, 516, 523, 551, 556, 559, 563, 567, 569, 575, 581, 591, 593, 597, 599, 601, 603, 607, 609, 623, 633, 647, 661, 667, 668, 673, 675, 677, 683, 684, 689, 692, 699, 701, 708, 709, 713, 716, 719, 725, 729, 733, 736, 739, 749, 756, 767, 772, 773, 779, 788, 789, 791, 793, 796, 797, 799, 807, 809, 812, 813, 816, 817, 827, 833, 837, 839, 844, 856, 857, 868, 877, 879, 881, 883, 887, 889, 893, 896, 899, 901, 907, 911, 917, 919, 925, 927, 937, 939, 956, 967, 977, 989, 991, 997]
|
| Előzmény: [3845] w, 2014-02-27 16:43:27 |
|
|
| [3844] Róbert Gida | 2014-02-27 14:15:20 |
 0<n<100 egészek közül pontosan a 11 többszörösei azok amelyeknek NINCS 10-csökkenő többszörösük: használjuk a 11-el való oszthatóságot (szám 11-el osztható, ha a0-a1+a2-a3+... osztható 11-el), és azt, hogy a szám 10- csökkenő.
Maradékra meg lehet írni egy programot, kis példa van mindegyikre, a legnagyobb n=89-re: 86*89=7654.
|
| Előzmény: [3843] w, 2014-02-27 12:36:36 |
|
|
| [3842] jonas | 2014-02-27 12:33:17 |
 552. (a) Nincs ilyen. Ugyanis bármely n pozitív egészre m=100 két nullára végződik, ezért nem lehet 10-csökkenő. Sőt, m>1010 esetén mn legalább 11 jegyből áll, ezért nem lehet 10-csökkenő.
(b) Nincs ilyen, mert már az (a)-nak sincs megoldása.
(c) Nincs.
|
| Előzmény: [3841] w, 2014-02-26 21:07:19 |
|
| [3841] w | 2014-02-26 21:07:19 |
 552. - m pozitív egész ("mn az n többszöröse")
Az 551. feladatból kimaradt, hogy nem szabad két e egyenesen lévő pont felezőmerőlegesét venni. Bocsánat. (Aztán feladat, hogy milyen mesével lehet ezt valóságszerűvé tenni. :-) )
|
| Előzmény: [3839] jonas, 2014-02-26 20:57:05 |
|
| [3840] jonas | 2014-02-26 21:00:04 |
 Az 551. feladat túl könnyűnek néz ki. Nem is értem, hogy az AB szakaszra mi szükség. Megoldás. Vegyél föl két pontot az e egyenesen, szerkeszd meg ezek f szakaszfelezőjét, ez merőleges e-re. Ezután vegyél két pontot f-en, ennek szerkeszd meg a szakaszfelezőjét, ez merőleges f-re ezért párhuzamos e-vel.
|
| Előzmény: [3837] w, 2014-02-26 20:01:14 |
|
|
| [3838] w | 2014-02-26 20:09:27 |
 B.4509 megfordításával adódik, hogy a húrnégyszög köré még egy parabola írható, melynek tengelye az eredeti paraboláéra merőleges, ezt és az eredeti parabolát elaffinítva további parabolákat kapunk, amik pedig B.4509 szerint húrnégyszögben metszik egymást, amely húrnégyszög az illeszkedéstartás szerint A'B'C'D'.
|
| Előzmény: [3832] Sinobi, 2014-02-11 16:29:21 |
|
| [3837] w | 2014-02-26 20:01:14 |
 Néhány témába illően szép feladat:
551. feladat. Adott egy AB szakasz, és egy e egyenes, ami áthalad a szakasz F felezőpontján. Rendelkezésünkre áll egy speciális szerkesztési eszköz, a szakaszfelező, ami két ismert ponthoz megrajzolja a tőlük egyenlő távol lévő pontok mértani helyét. Szerkesszünk csak szakaszfelezővel egy e-vel párhuzamos egyenest!
552. feladat. Nevezzünk egy k-alapú számrendszerbeli számot k-csökkenőnek, ha számjegyei balról jobbra olvasva szigorúan csökkennek.
(a) Van-e olyan n<100 pozitív egész úgy, hogy n bármely mn többszöröse a 10-csökkenő? (b) Van-e olyan n, amelyre igaz, hogy mn tetszőleges k-ra k-csökkenő? (c) Van-e végtelen sok ilyen n szám?
553. feladat. Legyenek a,b,n olyan pozitív egész számok, melyekre a100+b100 és a104+b104 osztható n-nel.
Igazoljuk, hogy a2014+b2014 is osztható n-nel!
|
|
|
| [3835] jonas | 2014-02-19 14:42:13 |
 Szerintem ez a szám a 1016949152542372881355932203389830508474576271186440677966, mert
6.1016949152542372881355932203389830508474576271186440677966=
6101694915254237288135593220338983050847457627118644067796
|
| Előzmény: [3833] Loiscenter, 2014-02-19 11:22:10 |
|
|
| [3833] Loiscenter | 2014-02-19 11:22:10 |
 szürgös:
Egy 6-ra végzödö szám ultolsó jegyét elhagyjuk. Ezt a szám elsö jegye elé irjuk. Az igy kapott szám hatsorosa az eredetinek. Melyik ez a szám? (azaz 6B = B6 . 6 ?)
|
|
| [3832] Sinobi | 2014-02-11 16:29:21 |
 Sinobi: "b, Bizonyítsd be, hogy ha van egy parabolán három pontpár (húr), amelyek felezőmerőlegesei egy ponton mennek át, akkor ha a hat pontot a parabola tengelyirányában elaffinítjuk, akkor az így kapott pontok felezőmerőlegesei is egy ponton fognak átmenni."
Azota sem tudom. Kedvcsinalonak egy hasonlo, de nagyon egyszeru feladat:
Ha van egy parabolan egy ABCD hurnegyszog, azaz barmelyik 2 pont felezomerolegese atmegy egy O ponton, akkor ha a hurnegyszoget a parabola tengelyiranyaban affinitom, akkor az A'B'C'D' pontnegyes is hurnegyszog lesz, azaz barmelyik ket pont felezomerolegese at fog menni O'-n.
Ez ugyan kovetkezik az elozo allitasbol, de azt nem tudom belatni, meg egyszerubben is kijon.
|
| Előzmény: [3795] Sinobi, 2013-10-12 01:30:53 |
|
|
| [3830] Fálesz Mihály | 2014-02-04 20:43:33 |
 Egy kapcsolódó feladat 2007-ből:
A. 429. Határozzuk meg mindazokat az egész együtthatós f(x) és g(x) polinomokat, amikre f(g(x))=x2007+2x+1.
A tanulság valami olyasmi, hogy polinomba polinom  deriválás... :-) deriválás... :-)
|
| Előzmény: [3829] w, 2014-02-03 23:18:11 |
|
| [3829] w | 2014-02-03 23:18:11 |
 550. feladat. (körülbelül)
a) Vannak-e olyan f,g,h másodfokú polinomok, melyekre az 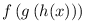 polinom pontosan az 1,2,3,4,5,6,7,8 helyeken nulla? polinom pontosan az 1,2,3,4,5,6,7,8 helyeken nulla?
b) Határozzuk meg azokat az f,g,h polinomokat, melyekre  . .
[Ezek nem nehéz, de érdekes feladatok. Ha eddig nem lett volna világos, aki ismeri őket, ne lője le. Aki maga megoldotta a feladatot, annak viszont szívesen látom megoldását.]
|
|
| [3828] Loiscenter | 2014-01-29 00:47:03 |
 1. legyen x=y=0 => f(0) = 0; 2) legyen x=y => 4f(x)[ f(x) - x.x] = 0 => vagy f(x) = 0 vagy f(x)=x.x külön x értékre
3) minden t# 0 esetére ha f(t) = t.t # 0 => legyen x=0, y=t => f(t).f(-t) =f(t)f(t) => f(-t) = f(t)=t.t; ha f(t) = 0 => legyen x=0, y=-t => f(t).f(-t) =f(-t)f(-t) => f(-t) = f(t)=0 összefoglalva f(-x)=f(x) minden x estére.
4) Ha létezik a# 0 ugy , hogy f(a)=0 => akkor minden t# 0 esetére legyen x=t, y=a => f(t+a)f(t-a) = f(t)f(t) legyen x=a, y=t => f(t+a)f(a-t) = f(t)f(t) - 4a.a.f(t) Mivel f(t-a) = f(a-t) => 4a.a.f(t) = 0 => f(t)=0
összegezve : f(x)=0 és f(x) = x.x; a két valosfüggvény , amely teljesiti a feltételt.
(Prof. Hung Son Nguyen - Varso egyetemból)
|
| Előzmény: [3827] Loiscenter, 2014-01-28 20:46:14 |
|
|
|
| [3825] nadorp | 2014-01-28 15:33:25 |
 Ez így egy kicsit hiányos.
Ugyanis abból, hogy minden x-re f2(x)=x2f(x) teljesül, csak az következik, hogy f(x)=0 vagy f(x)=x2, de ez még nem zárja ki azt, hogy pld f(2)=4 és f(5)=0 egyszerre teljesüljön.
|
| Előzmény: [3824] Loiscenter, 2014-01-28 15:17:44 |
|
| [3824] Loiscenter | 2014-01-28 15:17:44 |
 Legyen x=y=0 akkor f(0)=0 . legyen x=y igy f(2x)f(0)=4f(x)f(x) -4x.x.f(x) mivel f(0)=0 ezért 4f(x)f(x)-4x.x.f(x)=0 téhats f(x)=0 vagy f(x)=x.x . ellenörizve igaz mind.( bocsi nem tudtam hatványt irni)
|
| Előzmény: [3822] w, 2014-01-27 22:06:36 |
|
|
| [3822] w | 2014-01-27 22:06:36 |
 Egy "vicces" függvényegyenlet.
Keressük meg az összes f:R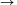 R függvényt a következő tulajdonsággal: R függvényt a következő tulajdonsággal:
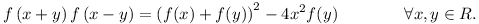
|
|
| [3821] aaaa | 2014-01-26 22:07:48 |
 Ebből még az is következik, hogy:
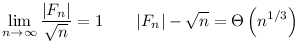
Ugyanis n 64-re 64-re 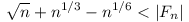 , mert van legalább egy 5-ik hatvány, egyébként finomítva a becslésedet (prímedik hatványokra elég nézni az összeget): , mert van legalább egy 5-ik hatvány, egyébként finomítva a becslésedet (prímedik hatványokra elég nézni az összeget):
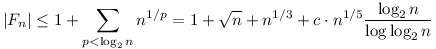
Ugyanis n-ig a prímek száma kb 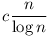 , ebből látszik, hogy elég nagy n-re , ebből látszik, hogy elég nagy n-re

|
| Előzmény: [3817] Ménkűnagy Bundáskutya, 2014-01-26 15:42:40 |
|
|
|
|
| [3817] Ménkűnagy Bundáskutya | 2014-01-26 15:42:40 |
 Azt hiszem, van egyszerűbb is.
Az n-nél kisebb k. hatványok száma legfeljebb n1/k. Itt a k legfeljebb log2n lehet: eltekintve az 1-től a 2 log2n. hatványával még számolni kell, többel biztosan nem. Azaz
|Fn| n1/2+n1/3+...+n1/log2n+1 n1/2+n1/3+...+n1/log2n+1 n1/2log2n+1, n1/2log2n+1,
ami n-nel osztva nyilván 0-hoz tart.
|
| Előzmény: [3815] aaaa, 2014-01-26 01:23:52 |
|
|
| [3815] aaaa | 2014-01-26 01:23:52 |
 Gondolom azt szeretnéd kérdezni, hogy ha Fn={n-nél kisebb hatványszámok}, akkor mi lesz
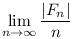
Lemma 1. 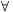  , , >0 >0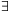 k0, hogy k>k0 esetén: k0, hogy k>k0 esetén:
![\left|\sum_{i=k}^{[k(1+\varepsilon)] }\frac{1}{i}-\log(1+\varepsilon)\right|<\delta](/kep/keplet.cgi?k=87DEA5C07E25C7AF)
Ez a szokásos integrálós becslésből kijön, legyen ez házi feladat.
Lemma 2. Ha ai pozitív egészek egy növekvő részsorozata, és 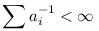 , akkor n-1|An| , akkor n-1|An|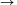 0, ha n 0, ha n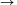 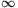 , ha An={ai|ai<n} , ha An={ai|ai<n}
Indirekt, tegyük fel, hogy nem áll fent a bemutatott egyenlőség, vagyis létezik olyan  , hogy |An|> , hogy |An|> n végtelen sokszor. Ha nincs ilyen, akkor pont azt kaptuk, amit akartunk. Legyen n végtelen sokszor. Ha nincs ilyen, akkor pont azt kaptuk, amit akartunk. Legyen 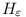 az ilyen n-ek halmaza, ekkor |H|=|N|, vegyük tehát egy olyan bi részsorozatát, ami tudja azt, hogy az ilyen n-ek halmaza, ekkor |H|=|N|, vegyük tehát egy olyan bi részsorozatát, ami tudja azt, hogy  kbi>bi-1, valamely k>2 egészre. Ekkor Abi> kbi>bi-1, valamely k>2 egészre. Ekkor Abi> bi miatt a [0,bi-1] intervallumba maximum bi-1< bi miatt a [0,bi-1] intervallumba maximum bi-1< kbi<Abi kbi<Abi k-1 darab eshet, szóval elég kevés szám, vagyis a számok legalább 1- k-1 darab eshet, szóval elég kevés szám, vagyis a számok legalább 1- k-1-edrésze a jó intervallumba esik. De ekkor az ide eső számok reciprokösszegére alsó becslést ad, ha az intervallumba eső legkisebb számokat vesszük, ebből legalább Abi-Abi-1=bi( k-1-edrésze a jó intervallumba esik. De ekkor az ide eső számok reciprokösszegére alsó becslést ad, ha az intervallumba eső legkisebb számokat vesszük, ebből legalább Abi-Abi-1=bi( - - k-1) darab van: k-1) darab van:
![\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq\sum_{i=[b_i-b_i \varepsilon+\varepsilon^k]}^{b_i}\frac{1}{i}\geq \log\left(1+\frac{\varepsilon-\varepsilon^k}{1-\varepsilon+\varepsilon^k}\right)-\delta](/kep/keplet.cgi?k=18D75B65BBB10C1D)
Az első lemma alapján. De legyen b1 akkora, hogy 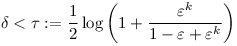 teljesüljön, így azt kaptuk, hogy teljesüljön, így azt kaptuk, hogy ![\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq \tau>0](/kep/keplet.cgi?k=423F09A30C0C85ED) De ekkor De ekkor
![\sum_{a_i<b_k} a_i^{-1}=\sum_{j=1}^{k}\sum_{a_i\in]b_{j-1},b_j]}\frac{1}{a_j}\geq\sum_{j=1}^{k}\tau=k\tau](/kep/keplet.cgi?k=7A2B5BC43AF17040)
Viszont így a reciprokösszeg nem lehet véges.
Lemma 3. A hatványszámok reciprokösszege kisebb, mint 2. Nézzük ugyanis a kövezkező összeget:

Viszont ab szerepel az a számhoz tartozó részlegösszegben, szóval a hatványszámok reciprokösszege véges.
Lemma 3 miatt teljesül Lemma 2. feltétele, így a hatványszámok felső sűrűsége 0 az egészek körében.
|
| Előzmény: [3814] Loiscenter, 2014-01-24 20:30:06 |
|
| [3814] Loiscenter | 2014-01-24 20:30:06 |
 Hatványszámok valoszinüsége természetes számok körében?
|
|
|
|
| [3811] w | 2013-11-10 16:59:08 |
 201314 mod 73 kiszámítása.
Bár klasszikus feladattípus, szerintem mégis érdekes a megoldás az átlagos feladathoz képest. (Például 999 mod 102 kiszámítása egyszerűbb, hiszen számológéppel is könnyen adódik, hogy 95 -1 (mod 102), ezért elég 99-t mod 10 vizsgálni, ami pedig könnyű.) Most az nem kunszt, ha Euler-Fermat-val lemészároljuk, ámde tökéletesen elfogadható megoldás (ezért tűztem itt ki). Ha egyszerűbb eszközökkel szeretnénk dolgozni, akkor a következő megoldást találhatnánk. -1 (mod 102), ezért elég 99-t mod 10 vizsgálni, ami pedig könnyű.) Most az nem kunszt, ha Euler-Fermat-val lemészároljuk, ámde tökéletesen elfogadható megoldás (ezért tűztem itt ki). Ha egyszerűbb eszközökkel szeretnénk dolgozni, akkor a következő megoldást találhatnánk.
Első célunk keresni olyan n kitevőt, melyre 20n  1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint 1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint

Tehát célszerű n=72 választása, hisz akkor az utolsó tag kivételével minden tag 73-nel osztható, vagyis 2049 -1 (mod 73). -1 (mod 73).
Vagyis csak 1314-t kell mod 49 megnéznünk. De a binomiális tételt újra alkalmazva kapjuk, hogy 1314 1 (mod 49), mert 13 1 (mod 49), mert 13 -1(7). Amiért az adódik, hogy 1314=49 -1(7). Amiért az adódik, hogy 1314=49 +1 alakú, ahol +1 alakú, ahol  tehát páros. Ebből következik, hogy 201314 tehát páros. Ebből következik, hogy 201314 20 (mod 73), vagyis az utolsó három számjegy 026. 20 (mod 73), vagyis az utolsó három számjegy 026.
|
| Előzmény: [3810] csábos, 2013-11-09 16:35:38 |
|
|
|
|
|
| [3806] w | 2013-11-07 16:09:11 |
 Nekem is van egy saját készítésű szép számelméletfeladatom, bár ez évszámok használatának árán könnyebb lesz.
Határozzuk meg a 201314 hatvány 7-es számrendszerbeli alakjában az utolsó három számjegyet.
|
|
| [3805] Sirpi | 2013-10-25 09:19:21 |
 Nekem is ez az eredmény jött ki, bár picit másképp csináltam.
Legyen a k jegyű. Ekkor
(a*)2=(a2)*=a2+11...1
(a*)2-a2=11...1
(a*-a)(a*+a)=11...1
11...1.(a*+a)=11...1
a*+a=11...1/11...1
Ha a k jegyű, akkor a2 vagy 2k-1, vagy 2k jegyű, tehát ennyi db. 1-es van az előző sorok jobb oldalán. Ezt osztjuk le az utolsó sorban egy k db 1-esből álló számmal, és könnyen látható, hogy csak akkor kapunk egész számot, ha 2k db egyesből áll a számláló (sőt, ellenkező esetben a* és a összege kisebb lenne, mint a különbsége).
Ez alapján a*+a=100...01 (k-1 db 0-val), a*-a=11...1, vagyis a=44...45, és ebből csak az 1 és a 2 jegyű megoldás a jó, ahogy azt Te is indokoltad.
|
| Előzmény: [3804] csábos, 2013-10-23 23:21:42 |
|
| [3804] csábos | 2013-10-23 23:21:42 |
 5,45
Tekintsük a feladatot modulo 10k. Legyen
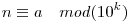
Ekkor a feladat az
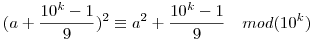
kongruencia formájában írható fel.
Négyzetre emelve, 81-gyel szorozva és a 10k-val osztható tagokat elhagyva a
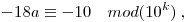
azaz
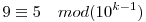
kongruenciához jutunk.
A jobboldalhoz 4.10k-t adva
a=44...445 adódik, azaz az eredeti kongruencia megoldásai
444...445 és 944...445. Ez utóbbi nem játékos, így marad az előbbi.
Ha k legalább 3, akkor 197136=4442<a2<4452=198025. Ezért a2 második jegye 9-es, azaz nem megoldás.
|
| Előzmény: [3803] Sirpi, 2013-10-21 14:26:41 |
|
| [3803] Sirpi | 2013-10-21 14:26:41 |
 A következő egy általam kitalált feladat:
Egy a természetes számra a* jelölje azt a számot, amit úgy kapunk, hogy a minden számjegyét eggyel megnöveljük. Pl: 125*=236. Ha egy számban szerepel 9-es számjegy, akkor nincs értelmezve.
Oldjuk meg az (n*)2=(n2)* egyenletet.
|
|
|
|
|
|
|
|
| [3796] Zilberbach | 2013-10-12 19:48:25 |
 Ebben a témában nem tördeli be a túl hosszú sorokat a gépem/programom. Mi lehet az oka?
|
|
| [3795] Sinobi | 2013-10-12 01:30:53 |
 Kaptam egy "érdekes" geometria feladatot, nem tudom mit lehetne vele kezdeni, ami nem kórdináta.
a, Ha van egy e egyenes, és egy p parabola, szerkeszd meg azokat a pontokat a parabolán, amelyek felezőmerőlegese az egyenes. (eddig nem volt nehéz)
b, Bizonyítsd be, hogy ha van egy parabolán három pontpár (húr), amelyek felezőmerőlegesei egy ponton mennek át, akkor ha a hat pontot a parabola tengelyirányában elaffinítjuk, akkor az így kapott pontok felezőmerőlegesei is egy ponton fognak átmenni.
c, Ily módon egy parabola és egy affinitás meghatároz egy  tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy  egyenestartó. egyenestartó.
|
|
| [3793] csábos | 2013-10-11 12:57:17 |
 Kedves HOA!
A probléma Steinerig és Fermat-ig visszavezethető. http://en.wikipedia.org/wiki/Steinertreeproblem Sőt, mér a Gyilkos számok egyik jelenetében is láttam. 2. évad Toxin című rész, 31. perctől. A kérdésem igazából arra vonatkozott, hogy a komplex számos megoldás-felvetés honnan ered. Ami még igazán érdekel: Minél korábbi előfordulása az
x2+xy+y2=a
x2+xz+z2=b
z2+zy+y2=c
típusú feladatnak.
Tud valaki erről valamit?
|
| Előzmény: [3792] HoA, 2013-10-10 16:48:43 |
|
| [3792] HoA | 2013-10-10 16:48:43 |
 Hát igen, mint a Ludas Matyi mottója mondta. „Nincsenek régi viccek, csak öreg emberek. Egy újszülöttnek minden vicc új” Nem emlékszem, hol láttam először, talán valamelyik Reiman könyvben. Most az interneten rákeresve ezt találtam legelőször:
Nemzetközi matematikai diákolimpiák (1959–2003)books.google.hu/books?isbn=9639548049 610 – 611. old.
http://books.google.hu/books?id=nNihkOMB8qYC&pg=PA610&lpg=PA610&dq=izogon%C3%A1lis+pont&source=bl&ots=ocxjZNxUjz&sig=g6aMbTyKXDcQBRh57RTWfDsgGfM&hl=hu&sa=X&ei=Fa5WUoy9HauX5ATV84HIBw&ved=0CGQQ6AEwCw#v=onepage&q=izogon%C3%A1lis%20pont&f=false
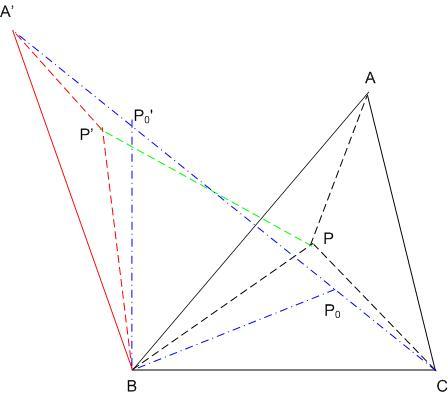
A lényeg: A 120 fokosnál nem nagyobb szögű háromszög síkjának az a pontja, melynek a csúcsoktól mért távolságösszege minimális, az izogonális pont. Bizonyítás: Legyen az ABC háromszög síkjának egy pontja P. Forgassuk el az ABP háromszöget B körül 60 fokal , új helyzete A’BP’ ( A’ az AB egyenes C-t nem tartalmazó oldalán ) . Ekkor A’P’ = AP, BPP’ háromszög szabályos, BP = BP’ = PP’ . A P pont csúcsoktól mért távolságainak összege AP + BP + CP = A’P’ + P’P +PC , vagyis egyenlő az A’P’PC töröttvonal hosszával. Mivel A’ és C helyzete P-től független, ez a hossz akkor a legkisebb, ha ha egybeeseik az A’C szakasszal. A minimális távolságösszeget adó P0 pont ( és 60 fokos elforgatottja , P0’ ) rajta van A’C –n, BP0P0’ szabályos, így BP0C szabályos, így BP0C =120o és BP0’A’ =120o és BP0’A’ =120o miatt BP0A =120o miatt BP0A is 120o is 120o
[3791]-re: Nézd meg, mi a helyzet, ha ABC >120o >120o
|
 |
| Előzmény: [3790] csábos, 2013-10-09 21:17:40 |
|
| [3791] csábos | 2013-10-09 22:21:43 |
 Természetesen a létezés bizonyításánál. Kavics mindig a tanteremben röpködő piros krokodilokkal példálózott. Ha azok léteznek, akkor minden igaz. A konstrukció mindig nehezebb a bizonyításnál. Ha feltesszük, hogy valami van, arról már könnyebb bármit igazolni.
|
| Előzmény: [3781] HoA, 2013-09-04 23:31:16 |
|
|
|
| [3788] HoA | 2013-10-04 22:04:07 |
 Azért írta ki furán, mert a százalék jelet megjegyzés kezdetének veszi, és mindent elhagy, amit a sorban utána írsz . Valamelyik témában nemrég volt szó róla. Tehát így kell írni, hogy látható legyen: \%
A feladattípus elég közismert. Nekem van egy egész kis könyvem belőlük. És persze egy táblázatos módszerrel elég automatikusan megoldható.
Az, hogy az emberek hány %-a képes megoldani, kicsit nézőpont kérdése. Készséggel elhiszem, hogy ha 100 embernek feladod, csak 1-2 -től kapsz megoldást. Nem azért, mert képtelen lenne megoldani, de nem érdekli annyira, hogy végigküzdje. Más lenne a helyzet, ha az élete - na jó, a havi fizetése függne tőle.
|
| Előzmény: [3787] koma, 2013-10-04 20:25:34 |
|
| [3787] koma | 2013-10-04 20:25:34 |
 -De furán írta ki-, szóval állítólag az emberek két százaléka tudja megoldani, és szerintem azért jóval többen képesek lehetnek rá, ti hogyan vélekedtek?
|
| Előzmény: [3786] koma, 2013-10-04 20:22:50 |
|
| [3786] koma | 2013-10-04 20:22:50 |
 Sziasztok, a véleményetekre lennék kíváncsi, szerintem nagyon sokan ismeritek a feladványt:
Ezt a feladatot Einstein írta. Azt mondta, hogy az emberek 98
Tények: 1. 5 ház van, különböző színüek. 2. Minden házban él egy-egy ember, mindegyik más nemzetiségű. 3. Az öt tulajdonos különböző italokat fogyaszt, különféle cigit szív és más-más állatot tart. 4. Nincs két olyan tulajdonos aki ugyanazt az állatot tartaná, ugyanazt a cigit szívná, vagy ugyanazt az italt inná.
1. A brit a piros házban lakik. 2. A svéd kutyát tart. 3. A dán teát iszik. 4. A zöld ház a fehér ház bal oldalán van. 5. A zöld ház tulajdonosa kávét iszik. 6. Az a személy aki Pall Mall-t szív madarat tart. 7. A sárga ház tulajdonosa Dunhill-t szív. 8. Az az ember aki a középső házban lakik tejet iszik. 9. A norvég az első házban lakik. 10. Az ember aki Blend cigit szív amellett lakik aki macskát tart. 11. Az az ember aki lovat tart amellett lakik aki Dunhill cigit szív. 12. A tulaj aki Blue Mastert szív, sört iszik. 13. A német Prince-t szív. 14. A norvég a kék ház mellett lakik. 15. Az ember aki Blend-et szív, a vizet ivó ember szomszédja.
-Én 20-25 perc alatt megoldottam, de nem érzem úgy, hogy a felső 2
|
|
|
| [3784] Ali | 2013-09-13 10:38:22 |
 Legyen g(x)=f(x)-x, és gn(x)=g(g(...g(x)...)). Az értelmezési tartományra tett megszorítás miatt g(x) 0 0 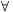 x x 0 esetén. 0 esetén.
Megoldva a gn+2(x)+gn+1(x)-2gn(x)=0 másodfokú lineáris rekurziót ( g0(x):=x, g1(x)=g(x) ),
gn(x)=(-2)n[x-g(x)]/3 +[2x+g(x)]/3, n 2 2
Ha x>g(x), akkor elég nagy páratlan n-re, míg x<g(x) esetén elég nagy páros n-re ellentmondás. Így g(x)=x és f(x)=2x.
|
| Előzmény: [3777] w, 2013-09-02 22:15:48 |
|
|
| [3782] juantheron | 2013-09-10 05:54:02 |
 Solution for real a,b,c in
a[a]+c{c}-b{b}=0.16
b[b]+a{a}-c{c}=0.25
c[c]+b{b}-a{a}=0.49
Where [x]= Integer part of x
and {x}= fractional part of x
|
|
| [3781] HoA | 2013-09-04 23:31:16 |
 A :-) -ból sejtem, észrevetted, hogy ez valójában a közismert izogonális pontos megoldás átírva komplexre.
A feladat talán éppen ezért érdekes: Hogyan derül ki a komplex megközelítésből, hogy a módszer csak 120o -nál kisebb szögű háromszögre működik?
|
| Előzmény: [3780] Fálesz Mihály, 2013-09-04 18:44:31 |
|
|
| [3779] HoA | 2013-09-04 10:54:29 |
 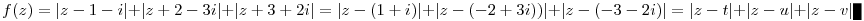 , ahol t=1+i,u=-2+3i,v=-3-2i Legyen továbbá z'=z-u,t'=t-u,v'=v-u . , ahol t=1+i,u=-2+3i,v=-3-2i Legyen továbbá z'=z-u,t'=t-u,v'=v-u . 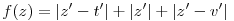 . Felhasználjuk, hogy . Felhasználjuk, hogy 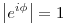 és és  ( ujjgyakorlat ) . Legyen ( ujjgyakorlat ) . Legyen 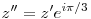 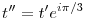 Ekkor Ekkor
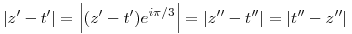
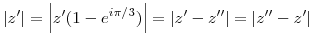
és innen a sokszög egyenlőtlenség miatt
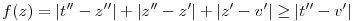
Numerikusan 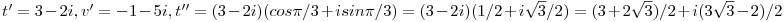 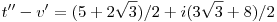 . . 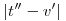 ~ 7,84 ~ 7,84
Feladatnak hagyom annak bzonyítását, hogy létezik is olyan z' - és innen z - érték, melyre f(z) felveszi minimális értékét – például a megfelelő z kiszámításával.
|
| Előzmény: [3775] juantheron, 2013-09-02 21:15:26 |
|
| [3777] w | 2013-09-02 22:15:48 |
 A következő függvényegyenlet leginkább a megoldási módszere miatt hasznos/érdekes 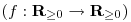 : :
f(f(x)-x)=2x.
|
|
|
| [3774] w | 2013-08-11 16:48:19 |
 Igen. Sok, az előbbihez hasonló feladat generálható. Olyan  szám kell nekünk, melyre az szám kell nekünk, melyre az
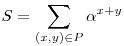 (*) (*)
összeg a lépések során invariáns marad, ahol P jelöli a zsetonok helyeinek halmazát. Az előbbi feladatban  x+y= x+y= (x+1)+y+ (x+1)+y+ x+(y+1)-ra redukálódik a (*) egyenlet, ahol x+(y+1)-ra redukálódik a (*) egyenlet, ahol 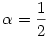 megfelel célunknak. Miért is? Úgy általában, olyan megfelel célunknak. Miért is? Úgy általában, olyan  számra van szükségünk, melyre számra van szükségünk, melyre
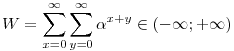 , ,
azaz az első síknegyed súlya véges. Ez éppen   (-1;+1) esetén következik be, és ekkor (-1;+1) esetén következik be, és ekkor
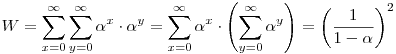
a mértani sor összegzőképlete szerint. A feladatokhoz pedig a P(x) polinomot rendelhetjük, amiről tudjuk, hogy van -1 és +1 között nemnulla gyöke, és tükrözi a zsetonok változását, azaz erre redukálódik a (*) egyenlet egy lépésnyi változás során. A VV-s példában ez a polinom P(x)=2x1-1 volt.
Aki ismer további alkalmazásokat erre a módszerre, örömmel olvasnám azokat.
|
| Előzmény: [3771] Micimackó, 2013-08-07 13:22:20 |
|
|
| [3772] aaaa | 2013-08-07 20:19:50 |
 a) ez ekvivalens n2 darab eredeti feladatbeli (kezdőhelyzet)->(véghelyzet) lehet-e kérdés megválaszolásával.
b) pl. (1;1)-re raksz, erre nem tudod az operációt alkalmazni.
|
| Előzmény: [3770] w, 2013-08-03 14:03:32 |
|
| [3771] Micimackó | 2013-08-07 13:22:20 |
 Megsúlyozzuk a mezőket, hogy egy érme mindig egyet érjen. Így 4 mező van, amiből 2-t akarunk üresen és két érmét akarunk a Fálesz verzióban, így ez nem lehet. A b) résznél még a szélső sorra és oszlopra is figyelni kell, mert ott is marad kis plusz üres terület és így nem lesz elég hely.
|
| Előzmény: [3768] w, 2013-08-02 22:28:38 |
|
| [3770] w | 2013-08-03 14:03:32 |
 Egyetértek, csak az eredeti feladatot akartam kitűzni. Lehetne bőven variálni a dolgokat: keressünk kezdő- és célhelyzeteket az (x,y)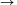 (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb. (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb.
Megkérdezném (a feladatot még nem gondoltam át): az (x,y)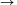 (x+1,y+1), (x-2,y-1) hasonló változatban legalább hány zsetont kell {(x,y): x,y egész} halmazra rakni, hogy sehogy se lehessen elérni, hogy mondjuk az (1,1)(1,10)(10,10)(10,1) négyzetben ne legyen zseton. (x+1,y+1), (x-2,y-1) hasonló változatban legalább hány zsetont kell {(x,y): x,y egész} halmazra rakni, hogy sehogy se lehessen elérni, hogy mondjuk az (1,1)(1,10)(10,10)(10,1) négyzetben ne legyen zseton.
|
| Előzmény: [3769] Fálesz Mihály, 2013-08-03 05:45:44 |
|
| [3769] Fálesz Mihály | 2013-08-03 05:45:44 |
 Nem értem, hogy az (a) rész miért ennyire bonyolult. Szerintem elég lenne három pont: (0,0), (1,0) és (0,1). Ha kezdetben csak ezeken van zseton, akkor akárhány lépés után is lesz legalább az egyiken.
|
| Előzmény: [3757] w, 2013-07-27 22:52:42 |
|
|
| [3767] Micimackó | 2013-08-02 21:06:06 |
 Nekem úgy tűnik nem lehet, mert nem férnek el. Az első bőven nem fér el (nem is marad elég hely a táblán), a másodikhoz már lenne elég hely, de nincs jól elosztva. Úgyhogy szerintem nem lehet.
|
| Előzmény: [3757] w, 2013-07-27 22:52:42 |
|
|
| [3765] Lóczi Lajos | 2013-08-01 11:04:27 |
 A célkifejezés négyzete azonosan egyenlő a nullára rendezett feltételi egyenletek egy másodfokú polinomjával. A konstans tag 1728-nak adódik, innen egy gyökvonás.
|
| Előzmény: [3762] w, 2013-07-31 12:57:17 |
|
|
|
|
|
|
|
| [3758] w | 2013-07-29 14:59:01 |
 Más. Legyen x,y,z>0. Tudjuk, hogy 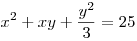 , , 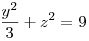 , z2+zx+x2=16. , z2+zx+x2=16.
Számítsuk ki xy+2yz+3zx értékét.
|
|
| [3757] w | 2013-07-27 22:52:42 |
 Egy további érdekes, hasznos, de nem annyira közismert feladat a Városok Viadaláról (1981):
Az első síknegyed rácspontjaira rakunk zsetonokat. Kezdetben (a) az origóban, az (1,0) és (0,1) és (1,1) és (0,2) és (2,0) pontokban van egy-egy zseton, (b) csak az origóban van zseton.
Egy lépésben az (x,y) rácspontból elveszünk egy zsetont - ha az (x+1,y) és (x,y+1) pontokban nincsen - majd utána az (x+1,y) és (x,y+1) pontokra rakunk egyet-egyet.
Elérhetjük-e az (a), illetve (b) esetben, hogy az (a) esetben megnevezett mezők egyikében sem szerepeljen zseton?
|
|
|
| [3755] w | 2013-07-27 21:47:12 |
 Állítás. Létezik c és d konstans a következő tulajdonsággal: tetszőleges a, b pozitív egész számpárhoz létezik pozitív egészekből álló m1,m2,...,mk számsorozat, melyre k<c.ln a+d és
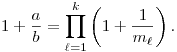
Ha igaz, próbáljunk minél kisebb c és d konstansokat keresni, ha hamis, akkor adjunk ellenpéldá(ka)t.
|
|
| [3754] Róbert Gida | 2013-07-27 21:46:59 |
 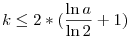 -re teljesül az állítás! Könnyen látható, hogy: -re teljesül az állítás! Könnyen látható, hogy: 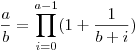 , itt a nevezők egymásutáni egészek; ezt fogjuk használni, hogy rövidebb szorzatot találjunk: vegyü észre, hogy , itt a nevezők egymásutáni egészek; ezt fogjuk használni, hogy rövidebb szorzatot találjunk: vegyü észre, hogy 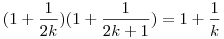 . Ezt az azonosságot alkalmazzuk az (első szinten), ekkor legfeljebb 2 tag marad ki a szorzatból (az első és az utolsó), míg az új . Ezt az azonosságot alkalmazzuk az (első szinten), ekkor legfeljebb 2 tag marad ki a szorzatból (az első és az utolsó), míg az új 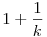 tagokban k egészek itt is egymásutáni egészek lesznek. Így ezt az azonosságot iterative tudjuk újra alkalmazni. Ha 2t-1 tagokban k egészek itt is egymásutáni egészek lesznek. Így ezt az azonosságot iterative tudjuk újra alkalmazni. Ha 2t-1 a<2t akkor t szint van és minden szinten megmarad legfeljebb 2 tag, azaz összesen legfeljebb 2t tag, de (t-1)ln 2 a<2t akkor t szint van és minden szinten megmarad legfeljebb 2 tag, azaz összesen legfeljebb 2t tag, de (t-1)ln 2 ln a, innen triviálisan kapjuk a bizonyítandót. ln a, innen triviálisan kapjuk a bizonyítandót.
|
| Előzmény: [3748] w, 2013-07-27 14:47:25 |
|
|
| [3752] w | 2013-07-27 20:19:56 |
 Jó, bocs, ez most kicsit sötét volt :-)
Kérlek akkor nézz utána a>1 esetének, vagy módosítsd a feladatot úgy hogy értelmes legyen. Felkérlek arra, hogy tégy hozzá valami építő jellegűet is.
|
| Előzmény: [3751] Róbert Gida, 2013-07-27 20:04:10 |
|
|
|
|
| [3748] w | 2013-07-27 14:47:25 |
 Állítás: Létezik c konstans a következő tulajdonsággal: tetszőleges a, b pozitív egész számpárhoz létezik pozitív egészekből álló m1, m2, ..., mk számsorozat, melyre k<c.ln a és
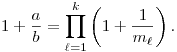
Igazoljuk vagy cáfoljuk.
|
|
| [3747] w | 2013-07-02 07:25:35 |
 Én leginkább erre gondoltam (5. feladat). Lineáris algebrából kb. semmit sem tudok, de úgy látszik, hogy a te megoldásodat írták át elemire. Van viszont lin. algebrakönyvem, előbb-utóbb belenézek. Elnézést a késő válaszért.
Üdv.: w
|
| Előzmény: [3746] jonas, 2013-06-21 21:08:33 |
|
| [3746] jonas | 2013-06-21 21:08:33 |
 Ez szerintem egy tanulságos feladat, mert lineáris algebrát tanít. Hadd mondjam el, én hogy képzelem el.
Az hogy egy (x1,x2,x3,x4) vektor négyzetes, ekvivalens azzal, hogy felírható (a,b,c)N alakban, ahol N a következő mátrix.

Legyen N első három oszlopa által alkotott V mátrix, és legyen az utolsó oszlop v.
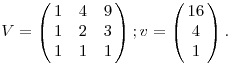
V egy Vandermonde mátrix, ezért invertálható. Ezért aztán bármely (x1,x2,x3) vektort pontosan egyféleképpen lehet négyzetes (x1,x2,x3,x4) számnégyessé befejezni: úgy, hogy x4=(x1,x2,x3).V-1.v. (A V-1.v vektor pontos (1,-3,3)T értékére nem lesz szükségünk a bizonyításhoz.)
Mármost rakjuk a feladatban adott számokat mátrixokba:
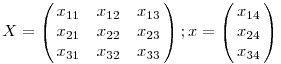
y=(x41,x42,x43)
Az, hogy a sorok négyzetesek, pont azt jelenti, hogy x=X.V-1.v és hogy x4=y.V-1.v. Mivel az első három oszlop is négyzetes, y=vt.(VT)-1.X. Ebből viszont
x4=y.V-1.v=vt.(VT)-1.X.V-1.v=vt.(VT)-1.x,
tehát az utolsó oszlop is négyzetes.
|
| Előzmény: [3745] w, 2013-06-21 14:15:10 |
|
| [3745] w | 2013-06-21 14:15:10 |
 Nevezzünk egy (t1,t2,t3,t4) valós számnégyest négyzetesnek, ha léteznek a, b, c valós számok, melyekre 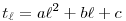 teljesül teljesül  =1,2,3,4-re. Az alábbi táblázatban (xi1,xi2,xi3,xi4) (i=1,2,3,4) négyzetes számnégyesek. Mutassuk meg, hogyha (x1j,x2j,x3j,x4j) j=1,2,3 esetén négyzetes, akkor j=4-re is. Általánosítsunk. =1,2,3,4-re. Az alábbi táblázatban (xi1,xi2,xi3,xi4) (i=1,2,3,4) négyzetes számnégyesek. Mutassuk meg, hogyha (x1j,x2j,x3j,x4j) j=1,2,3 esetén négyzetes, akkor j=4-re is. Általánosítsunk.

|
|
| [3744] aaaa | 2013-06-15 17:10:57 |
 Igazából a következő jutott eszembe, nem tudom mennyire nehéz: Legyen H egy olyan véges halmaz, amelynek elemei olyan szakaszhalmazok, melyek egész koordinátájú, szomszédos pontokat kötnek össze. Legyen S is egy ilyen halmaz, elemei Si. (S megszámlálhatóan végtelen, elemei nem vihetők egymásba tükrözésekkel, forgatásokkal, eltolásokkal). Mérjük H lefedőképességét S-re nézve a következőképpen: fH(si):=1, ha si S lefedhető H-beli elemek eltoltja, elforgatottja vagy tükrözött verziójaival, átfedés nélkül, és különben 0, és definiáljuk a S lefedhető H-beli elemek eltoltja, elforgatottja vagy tükrözött verziójaival, átfedés nélkül, és különben 0, és definiáljuk a 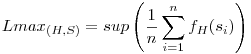 és és 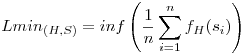 értékeket. Legyen H triviális halmaz, ha minden eleme összefüggő, és lefedhető egy elég nagy szakasszal. értékeket. Legyen H triviális halmaz, ha minden eleme összefüggő, és lefedhető egy elég nagy szakasszal.
Ezek után kellene megadni valami értelmes rendezést S elemeire, hogy kikerüljük azt, hogy bárhogy átrendezhetjük az S halmazt, és ezután lenne értelme a következőknek:
Ezek után kérdések: Van-e olyan S halmaz, amelyre Lmax(H,S) Lmin(H,S)? Lmin(H,S)?
Lehet-e úgy megadni halmazokat, hogy Lmin(H,S)=Lmax(H,S)=r irracionális legyen?
Ugye itt azt láttuk be, hogy ha H= {négyzet,L-betű}, S={négyzethálók}, akkor Lmin(H,S)=Lmax(H,S)=0
|
| Előzmény: [3737] aaaa, 2013-06-11 19:02:07 |
|
|
|
|
|
|
| [3738] uborkalekvar | 2013-06-12 17:19:31 |
 Sziasztok!
Valaki tudna segíteni ebben a 2 feladatban?
1. a.Hányféleképpen juthatunk el a koordináta-rendszerben az origóból a (7,6) pontba, ha egy lépés során csak jobbra, illetve felfelé léphetünk 1 egységet? b.Hány esetben haladunk át a (3,4) ponton?
2.Hány olyan valódi hatjegyű páros szám van, amely nagyobb 400000-nél és van benne ismétlődő számjegy?
Köszönöm előre is a segítséget!
|
|
| [3737] aaaa | 2013-06-11 19:02:07 |
 valóban igazad van, butaság, amit írtam. Újra nekifutva: Tegyük be a hálót egy koordinátarendszerbe, (0;0) legyen az egyik csúcs, egység hosszú oldala legyen a négyzeteknek, legyen a rács tengelypárhuzamos n*n-es háló, ahol n>5, az (x,y), (x,y+1) szakaszt jelölje (x,y+0.5) s (x,y), (x+1,y)-t (x+0.5,y). Az L-betűt a 2 szakasz 3 végpontjával adjuk meg, a négyzetet meg (x+0.5,y+0.5) alakban.
Na most nézzük a (0;0) sarkot. Ha L-betű van itt, akkor az (2,0)-(0,0)-(0,2), mert különben (0,0)-(0,2)-(2,2)-t és (0,0)-(2,0)-(2,2)-t használjuk, de ekkor (1,0.5) és (0.5,1) nem fedhető le átfedés nélkül. Így leraktuk a (2,0)-(0,0)-(0-2) L-betűt. Ekkor (1,0.5) és (0.5,1) csak egyféleképp fedhetők, (1,0)-(1,2)-(3,2)-vel és (0,1)-(2,1)-(2,3)-al. Ezután (2,0.5) és (0.5,2) csak (2.5,0.5)-el és (0.5,2.5)-el fedhető. Ezután (0,3.5) és (3.5,0) fedéséhez kell (0,3)-(0,5)-(2,5) és (3,0)-(5,0)-(5,2). Most ha ránézünk (4,0.5), (0.5,4)-re, akkor muszáj (4,0)-(4,2)-(6,2)-t és (0,4)-(2,4)-(2,6)-t lerakni, de ekkor (1,3.5) és (3.5,1) nem fedhető semmivel.
Konklúzió: a sarokban négyzet van, ha legalább 6*6-os négyzetről van szó, vagyis (0.5,0.5)-t fel kell használni. De ekkor (0,1.5)-t és (1.5,0)-t csak (0,1)-(0,3)-(2,3) és (1,0)-(3,0)-(3,2) fedheti, és ettől fogva (0,2n+1.5)-t és (2n+1.5,0)-t csak (0,2n+1)-(0,2n+3)-(2,2n+3) és (2n+1,0)-(2n+3,0)-(2n+3,2) fedheti.
Összefoglalva: egy legalább 6*6-os négyzet jó lefedésénél minden sarokban négyzet van, és a határszakaszokat egyértelműen fedik az L-betűk. De ekkor 2 eset van: ha n=2k+1, akkor lesz egy szakasz minden határon, amit nem tudunk lefedni, ha n=2k, akkor meg a négyzetektől induló L-betűk egymást fogják fedni, ahol a két sarokhoz tartozó L-betűk találkoznak.
A kimaradó kérdések: n=2,3,4,5-re van-e lefedés
n=2-re trivi, hogy nincs
n=3-ra (0.5,2.5), (2.5,0.5), (2.5,2.5), (2,0)-(0,0)-(0,2), (1,0)-(1,2)-(3,2) és (0,1)-(2,1)-(2,3) jó fedés
n=4-re L-betűs sarkos érvelés megakad (0,3.5) és (3.5,0)-nál, a négyzetes igaz rá, nincs fedés
n=5-re L-betűs sarkos érvelés megakad (4,0.5) és (0.5,4)-nél, a négyzetes igaz rá, nincs fedés
Összefoglalva: csak és kizárólag n=3-ra rakható ki.
|
| Előzmény: [3736] w, 2013-06-10 22:22:03 |
|
| [3736] w | 2013-06-10 22:22:03 |
 Nagyon vázlatos. "A másik 2 oldal ekkor nem fedhető le egyszerre ezekkel a típusú darabokkal átfedés nélkül." Átfedés alatt azt értem, hogy két darabnak közös szakasza van. Metszhetik még egymást. (Nem tudom, erre gondoltál-e.)
|
| Előzmény: [3734] aaaa, 2013-06-10 00:08:48 |
|
| [3735] jonas | 2013-06-10 09:55:57 |
 Négyzet alakú drótdarabokkal nyilván nem lehet, mert ezek a rács szélét nem tudják lefedni. Azt nem tudom, hogy L alakú darabokkal mi a helyzet.
|
| Előzmény: [3733] w, 2013-06-06 09:21:45 |
|
| [3734] aaaa | 2013-06-10 00:08:48 |
 Nem, L-betűt nem használhatunk a kirakáshoz, ugyanis tekintsük az L-betű "csúcsánál" lévő négyzetet, amelynek 2 oldala az L-betűbe esik. A másik 2 oldal ekkor nem fedhető le egyszerre ezekkel a típusú darabokkal átfedés nélkül. Csak négyzetekkel meg nem lehet lefedni. (megj. ez minimum 2*2-es négyzethálóra is igazolja, hogy nem lehet)
|
| Előzmény: [3733] w, 2013-06-06 09:21:45 |
|
| [3733] w | 2013-06-06 09:21:45 |
 Aha értem. Akkor témát váltok: ki lehet-e rakni egy 8x8-as négyzetrácsot átfedés nélkül a szimmetrikus, négy egységszakaszból álló L-alakú, illetve négyzet alakú drótdarabkákkal?
|
| Előzmény: [3732] aaaa, 2013-06-06 08:31:09 |
|
| [3732] aaaa | 2013-06-06 08:31:09 |
 azt a megoldást ismerem máshonnét, és épp ezért nem azt írtam le, meg most már ez a becsléssorozat egy kicsit kézenfekvőbb volt :)
|
| Előzmény: [3731] w, 2013-06-06 08:21:32 |
|
| [3731] w | 2013-06-06 08:21:32 |
 Lehet tanulságossá tenni. Kezdd azzal, hogy a feladatot megpróbálod szépen megoldani. Van igen szép, integrálos egyenlőtlenség nélküli megoldása, csak ahhoz gondolkodni is kell :-) Segítség: mi indukciót akarunk csinálni, csak n-re nem sikerül. Azt igazold, hogy g(n)<3.
|
| Előzmény: [3730] aaaa, 2013-06-05 22:45:26 |
|
| [3730] aaaa | 2013-06-05 22:45:26 |
 Utóbbi alsó korlátja triviálisan a 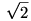 , felsőre meg logaritmálunk, szóval a következőt kéne minél jobban becsülni: , felsőre meg logaritmálunk, szóval a következőt kéne minél jobban becsülni:
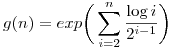
Mivel 2log x<x-1, ha x>4, ezért mehet a következő felső becslés: 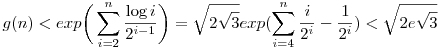
Ha meg nem becsülünk így felülről, hanem integrállal becsülgetünk, akkor n=10-től indítva az integrált felső korlátnak 2.76676 adódik pl, de ez nem túl tanulságos.
|
| Előzmény: [3729] w, 2013-06-05 21:33:20 |
|
| [3729] w | 2013-06-05 21:33:20 |
 További algebrai ügyeskedés (ami nagyon tetszik) ennek a topicnak az első hozzászólásaiban található: mennyi lesz az
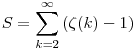
összeg, ha  (k) a híres Riemann-féle zéta-függvény. Riasztóbb, mint amilyen. (k) a híres Riemann-féle zéta-függvény. Riasztóbb, mint amilyen.
Új feladat következik. Egy másik függvényt mondok, pl. g-t, ami ezúttal a pozitív egészek közül a 2-nél nagyobbakra hat, és nem más, mint

lesz. Most nem puccoskodok, csak kérem, hogy mutassuk meg, hogy g felülről és alulról korlátos. Adjunk meg minél jobb korlátot.
|
| Előzmény: [3728] aaaa, 2013-06-05 21:22:05 |
|
| [3728] aaaa | 2013-06-05 21:22:05 |
 Hú, tényleg, pozitívakra gondoltam. Igen, bernoulliból szépen kijön, vagy még a b) feladat szorzatának felső becsülgetéséből is pont ez adódik.
|
| Előzmény: [3727] w, 2013-06-05 21:12:46 |
|
| [3727] w | 2013-06-05 21:12:46 |
 Aranyos. Nekem pozitív egészekre van megoldásom, de nem is baj, mert csak poz. egészekre értelmezhetők a kifejezések, vagy teljesül az egyenlőtlenség. (Utóbbi magyarázata: ha n=1 és m<0, akkor a bal oldal 1-1/(-m), a jobb oldal 1+0, ami ellentmondás.) A Bernoulli-egyenlőtlenség szerint
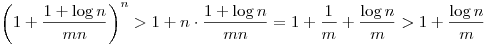
és ebből n-edik gyököt vonva megkapjuk a kívántat.
Már aki nem ismeri a Bernoullit, az kínos helyzetben van, mert vagy eszébe jut a súlyozott hatványközepek közötti egyenlőtlenség (ami bizonyítja a Bernoullit), vagy (nagyobb eséllyel) rájön, hogy itt indukciót lehetne csinálni. Ennek ellenére a feladat legkönnyebb megoldása a binomiális tétellel történik (megint ekvivalens átal. n-edikre hatványozok):
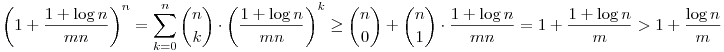
|
| Előzmény: [3726] aaaa, 2013-06-05 20:02:28 |
|
| [3726] aaaa | 2013-06-05 20:02:28 |
 Bizbe, hogy:
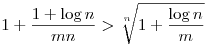
minden egész n és m párra.
|
|
| [3725] aaaa | 2013-06-05 19:53:28 |
 Remélem azért nem írtam el sehol, de:
a) Legyen:
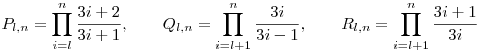
Ekkor Ql,n+1>Pl,n>Rl,n>Ql,n, ez pl. tényezőnkénti összehasonlítással adódik, az alsó ill felső becsléshez használt PQR típusú két szorzat meg teleszkópos, lesz. Ekkor
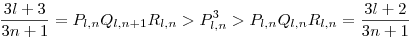
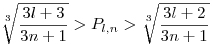
A feladatban l=2666, n=333, így 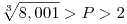 adódott. adódott.
b) Először is, ha xi>0 teljesül a következő, egyenlőség i=1 esetén:

Vagyis, felhasználva 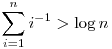 -et: -et:
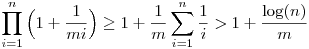
Szóval minden m>0-ra tart a végtelenbe.
|
| Előzmény: [3724] w, 2013-06-05 15:27:35 |
|
| [3724] w | 2013-06-05 15:27:35 |
 Definiáljuk a pozitív egész számokon értelmezett f(n,m) függvényt a következőképpen:
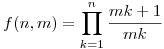 . .
(a) Nagyobb vagy kisebb a
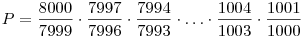
kifejezés a kettőnél?
(b) Mely m számok esetén lesz 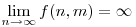 ? ?
|
|
|
|
| [3721] w | 2013-05-26 19:31:50 |
 Ennek mintájára igazoljuk, hogy
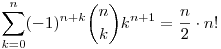
|
|
| [3720] w | 2013-05-26 19:26:07 |
 Visszatérve Lajos problémájára, helyettesítsünk be A=0, h=1-et, és vegyük az f(x)=xn polinomot!
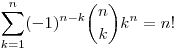
Ilyen formára írtam át korábban az összegét, ami tehát valóban 1-gyel egyenlő.
Amúgy ez elvileg ismert azonosság volna, úgyhogy egy kombinatorikai megoldást szívesen megnéznék.
|
| Előzmény: [3719] w, 2013-05-26 19:17:40 |
|
| [3719] w | 2013-05-26 19:17:40 |
 Olvasgatás közben rábukkantam a következő azonosságra:
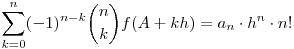
ahol f(x)=anxn+an-1xn-1+...+a1x+a0, f R[x] polinom, h R[x] polinom, h 0, A valós számok, n pozitív egész. 0, A valós számok, n pozitív egész.
Vajon hogyan igazolnánk?
Nemrég merült fel a következő segédfeladat. Keressük meg az összes legfeljebb n-edfokú p polinomot, amelyre adott páronként különböző a0, a1, ..., an és x0, x1, ..., xn számok mellett p(xi)=ai (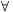 i=0,1,...n)! i=0,1,...n)!
Megoldás. Először megbecsüljük, hány ilyen polinom lehet. Tegyük fel, hogy két különbözőt is találtunk. Ekkor a két polinom különbsége (n+1) db helyen (x0, x1, ..., xn helyeken) nulla, bár legfeljebb n-edfokú, azaz csakis a zéruspolinom lehet, ami ellentmond annak, hogy különböző polinomokat vettünk. Idő kérdése, amíg konstruálunk is egyet:
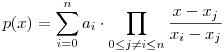
xi behelyettesítés után láthatóan jó lesz.
Ezt hívják a Lagrange-féle interpolációs polinomnak (amit gondolom a hozzászólók nagy része ismer).
Megoldás. Vegyük az f(x) legfeljebb n-edfokú függvényre felírt interpolációs képletet:
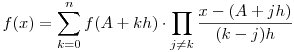
. Ezután nézzük meg a két oldalon álló polinomok főegyütthatóját!
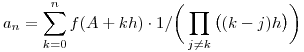
(Ugyanis az int. azonosságban minden egyes k-ra megnézve a tagot, a számlálóban lévő szorzat elvégzése után csak egy darab xn keletkezik.)
Az utóbbi kifejezés tovább alakítható:
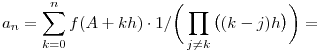
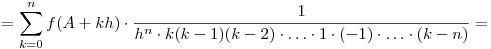
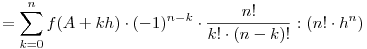
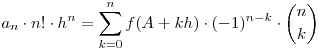
Készen vagyunk.
|
| Előzmény: [3717] Lóczi Lajos, 2013-04-22 01:41:38 |
|
| [3718] w | 2013-04-30 16:59:56 |
 Az összeget jobban szeretem a következő alakban:
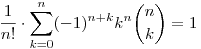 . .
(Direkt odaírtam, hogy az összeg valójában 1-gyel egyenlő. Ja meg itt n:=p, mert p általában prímet jelöl, továbbá az m betű futó indexben, kombinatorikai azonosságban nem tetszik nekem. Számomra ilyen formában sokkal áttekinthetőbb, de nem szeretnék erről vitát kezdeni.)
|
| Előzmény: [3717] Lóczi Lajos, 2013-04-22 01:41:38 |
|
|
| [3716] gyula60 | 2013-04-19 21:35:07 |
 Megoldandó a következő háromismeretlenes harmadfokú egyenlet, t=1,2 és 3 esetén:
t2·w3+t·v·(v2-3·u·w)+u3=1
Keress összefüggést a következő ciklikus mátrixszal:
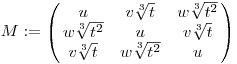
További előzmények: [3708],[3711],[3712],[3713]
|
| Előzmény: [3710] nadorp, 2013-04-13 09:28:54 |
|
|
| [3714] egyedülható | 2013-04-17 19:35:54 |
 Létezik-e olyan képlet,mely megadja,hogy egy adott számnál mikor lesz nagyobb a harmonikus sor értéke?
|
|
| [3713] gyula60 | 2013-04-13 16:34:47 |
 A klasszikus Csebisev polinomok és másodfokú Pell egyenlet között nyilvánvaló a kapcsolat. Az összekötő egyenletük lényegében egy másodrendű ciklikus mátrix determinánsával hozható összefüggésbe. Amire később mi kísérletet teszünk az, hogy megpróbálunk egy olyan polinom rendszert gyártani, ami egy harmadrendű mátrix determinánsával állítható elő. Ezt neveztem én hibásan 3711 utolsó mondatában "harmadfokú Csebisev polinom"-nak, holott többről lesz szó.
|
| Előzmény: [3711] gyula60, 2013-04-13 16:01:27 |
|
|
| [3711] gyula60 | 2013-04-13 16:01:27 |
 A feladat egyenlőre a harmadfokú háromismeretlenes Pell egyenlet egyik lehetséges, a harmadrendű ciklikus mátrixok alkalmazásával történő általánosítása. A lehetséges feltételek megkeresése, majd egy későbbi fázisban elgondolkozunk a negyedfokú változaton is. Még később a harmadfokú Csebisev polinomokat is megpróbáljuk előállítani.
|
| Előzmény: [3710] nadorp, 2013-04-13 09:28:54 |
|
| [3710] nadorp | 2013-04-13 09:28:54 |
 Legyen  n-edfokú algebrai szám, és legyenek n-edfokú algebrai szám, és legyenek  1= 1= , , 2,..., 2,..., n az n az  minimálpolinomjának gyökei. Tetszőleges x1,x2,,...,xn egész számokra tekinsük az minimálpolinomjának gyökei. Tetszőleges x1,x2,,...,xn egész számokra tekinsük az
f(x1,...,xn,x)=xnxn-1+...+x2x+x1 polinomot.
A feladatod szerintem arra vezethető vissza általában, hogy oldjuk meg az
 egyenletet az egész számok körében. egyenletet az egész számok körében.
|
| Előzmény: [3709] gyula60, 2013-04-12 17:35:08 |
|
| [3709] gyula60 | 2013-04-12 17:35:08 |
 A feladványom egyenletét eredetileg egy ciklikus mátrix determinánsával állítottam fel. Nyugodtan használhatsz gyökös kifejezéseket is. Ez a mátrixcsoport alkalmas lehet néhány alacsony fokszámú diofantoszi probléma kezelésére is.
|
| Előzmény: [3706] nadorp, 2013-04-11 16:05:24 |
|
|
|
| [3706] nadorp | 2013-04-11 16:05:24 |
 csak lusta voltam és ez már súrolja az egyetemi anyagot:-)
Ha 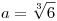 és (p,q,r) Q(a)-beli elem, akkor az inverzére és (p,q,r) Q(a)-beli elem, akkor az inverzére
(pa2+qa+r)(xa2+ya+z)=(rx+qy+pz)a2+(6px+ry+qz)a+6qx+6py+rz=1
Láthatóan egy lineáris egyenletrendszert kapunk, melynek mátrixa
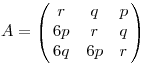 valamint jó jel, hogy |A|=36p3+6q3+r3-18pqr=1 valamint jó jel, hogy |A|=36p3+6q3+r3-18pqr=1
A szimmetria miatt ha (p,q,r) megoldása a diofantikus egyenletnek, akkor fenti egyenletrendszer x,y,z megoldása is az. Az előzőek alapján sejteni lehet, hogy ha (p,q,r) és (x,y,z) is megoldás, akkor 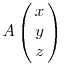 is megoldás lesz. Ez valóban így van, ezért innen indukcióval következik, hogy ha p,q,r megoldás, akkor is megoldás lesz. Ez valóban így van, ezért innen indukcióval következik, hogy ha p,q,r megoldás, akkor 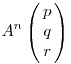 is megoldás tetszőleges n egészre ( negatív kitevő is megengedett, hiszen az A mátrix invertálható ). Innen az egyenlet megoldásai: is megoldás tetszőleges n egészre ( negatív kitevő is megengedett, hiszen az A mátrix invertálható ). Innen az egyenlet megoldásai:
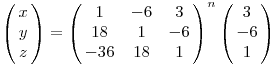
Ezt még "szebbé" lehet tenni, ha a mátrixot diagonizáljuk. Azt még nem láttam be, hogy több megoldás nincs. Ha pld. tudnánk, hogy z=1 esetén csak egy megoldás van és a rekurzió z-ben monoton, akkor ezzel is kész vagyunk.
|
| Előzmény: [3705] gyula60, 2013-04-11 13:27:06 |
|
|
|
| [3703] nadorp | 2013-04-07 10:28:50 |
 Igen, van összefüggés. Könnyű ellenőrizni, hogy tetszőleges p,q,r számokra
| (1) | p3+q3+r3-3pqr=(p+q+r)(p2+q2+r2-pq-pr-qr) |
Ezt alkalmazva a diofantikus egyenletedre, bevezetve az 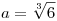 jelölést kapjuk jelölést kapjuk
36x3+6y3+z3-18xyz=(xa2+ya+z)((y2-xz)a2+(6x2-yz)a+z2-6xy)=1
Tehát, ha az egyenletnek az x,y,z számok megoldásai, akkor ez azt jelenti, hogy gyöktelenítéskor az y2-xz,6x2-yz,z2-6xy együtthatókat kell kapnunk. Esetünkben a 3,-6,1 számok kielégítik (1)-et, ezért gyöktelenítéskor a 33,60,109 együtthatókat kell, hogy kapjuk.
|
| Előzmény: [3700] gyula60, 2013-04-06 22:05:08 |
|
| [3702] w | 2013-04-07 09:18:45 |
 Próbáld meg faktorizálni. Ha k páros, a kifejezés is páros lesz, úgyhogy a páratlan k számok esete számít.
45(2k+1)+(5(2k+1))4=410k+5+(10k+5)4=...
(Már kiírtak megoldást a korábbi hozzászólásokban.)
|
| Előzmény: [3701] gyula60, 2013-04-06 23:09:43 |
|
| [3701] gyula60 | 2013-04-06 23:09:43 |
 Ha segít valamit az, hogy a számítógépem megnézte az összes 45k+(5k)4, (k=1,2,...,109) alakú számokat és false választ adott. Ebből talán felállítható egy sejtés, de a válasz nálam is meghaladja jelenlegi tudásomat.
|
| Előzmény: [3646] w, 2012-12-08 20:48:35 |
|
| [3700] gyula60 | 2013-04-06 22:05:08 |
 Szeretnék egy számelméleti problémát ismertetni:
Van-e kapcsolat a következő 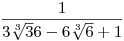 tört nevezőjének gyöktelenítése és a 36x3+6y(y2-3xz)+z3=1 háromismeretlenes diofantoszi egyenlet megoldása között, ha tudjuk, hogy a tört nevezőjének együtthatói adják az egyenlet egyik megoldását? tört nevezőjének gyöktelenítése és a 36x3+6y(y2-3xz)+z3=1 háromismeretlenes diofantoszi egyenlet megoldása között, ha tudjuk, hogy a tört nevezőjének együtthatói adják az egyenlet egyik megoldását?
|
|
|
| [3697] w | 2013-02-28 20:48:10 |
 Kicsit elbonyolítottad*: az
16(((s-b)(s-c))2+((s-c)(s-a))2+((s-a)(s-b))2) a4+b4+c4 a4+b4+c4
egyenlőtlenség AM-GM miatt nyilván igaz: pl.
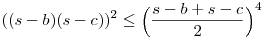 , ahol s-b+s-c=a. Innen egyenlőség esete is adódik. , ahol s-b+s-c=a. Innen egyenlőség esete is adódik.
-
*Persze ízlés kérdése, hogy teljes négyzetes alakra hozod-e.
|
| Előzmény: [3696] sakkmath, 2013-02-28 14:45:49 |
|
| [3696] sakkmath | 2013-02-28 14:45:49 |
 Használjuk fel Kiss György: Amit jó tudni a háromszögekről című cikkének eredményeit:
először az rra = (s-b)(s-c), rrb = (s-c)(s-a), rrc = (s-a)(s-b) összefüggéseket, később pedig a jól ismert, következő helyettesítéseket: s-a = x, s-b = y, s-c = z, illetve: a = y+z, b = z+x, c = x+y .
|
 |
| Előzmény: [3695] w, 2013-02-23 16:53:45 |
|
|
|
|
| [3692] w | 2013-02-21 22:08:17 |
 Köszönöm a hozzászólást, a Pedoe-egyenlőtlenséget nem ismertem, csak a Weitzenböck-öt és a Hadwiger-Finsler-t.
Egyetértek, a háromváltozós egyenlőtlenségek nem túl izgalmasak, leginkább a (még) több változós egyenlőtlenségekre való gyakorlásra vagy módszerek megismerésére. (Manapság még a KöMaL A-ban néha szerepel ilyen, pl. A.571, de mint láttuk, azt is végig lehet tolni akár AM-GM-mel is :-). )
Ha már egyenlőtlenségeknél tartunk, mutatok sajátot is (szokásos jelölésekkel):
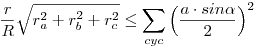 . .
Nem valami szép, sok minden bele van erőltetve, de azért van benne némi gondolkodás is.
Ezenkívül kitűznék egy nehezebb feladatot is, aki tud, mondjon megoldást.
|
| Előzmény: [3698] Fálesz Mihály, 2013-02-21 18:45:00 |
|
| [3698] Fálesz Mihály | 2013-02-21 18:45:00 |
 Bocs, a [3686]-ra akartam regálni, a [3688] elkerülte a figyelmemet.
A [3688]/a esetében valóban az a legegyszerűbb, ha új változókat vezetünk be, és ettől kezdve nincs háromszög, csak nemnegatív számok. (Btw, lehet egy lépéssel rövidebben, nincs szükség az xyz-vel való osztásra.)
A [3688]/b a (Neuberg-)Pedoe egyenlőtlenség egy változata, ami a KöMaL-ban is szerepelt (A. 468.). Ha két háromszög oldalai a,b,c, illetve A,B,C, a területük t, illetve T, akkor
a2(B2+C2-A2)+b2(C2+A2-B2)+c2(A2+B2-C2) 16tT. 16tT.
Egyenlőség akkor van, ha a két háromszög hasonló.
Abban a háromszögben, aminek az oldalai 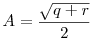 , , 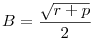 és és 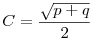 , azaz B2+C2-A2=p, C2+A2-B2=q és A2+B2-C2=r, a terület éppen , azaz B2+C2-A2=p, C2+A2-B2=q és A2+B2-C2=r, a terület éppen 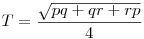 . .
(Mivel nem csak triviális esetekben van egyenlőség, ez elég nehézzé teszi a feladatot.)
* * *
Az érdekesség kérdéséről annyit, hogy sokezer háromváltozós szimmetrikus vagy ciklikus egyenlőtlenséget lehet találni az interneten, és ezeknek lényegében semmi üzenete vagy értelme nincsen. Egy időben voltak ilyenek az olimpián is, de miután egy csomó diák ráállt arra, hogy ilyeneket gyakoroljon tömegével, a háromváltozós egyenlőtlenségek háttérbe szorultak.
|
| Előzmény: [3691] w, 2013-02-21 15:26:54 |
|
| [3691] w | 2013-02-21 15:26:54 |
 "Hát, alaposan túlbonyolítottátok." - Ízlés kérdése, pl. szerintem a módszerem hasznosabb (a tiéd valóban szebb megoldás). Ezt mutatja, hogy a Te becslésed csak az eredeti egyenlőtlenségre jó (illetve egy csekély általánosításra), az (a) állításnál nem válik be.
"Csak tudnám, hogy ez az egyenlőtlenség miért "érdekes"..." - Az egyenlőtlenség (és főként az eredeti feladat) nem érdekes, ami érdekes, az az, hogy legalább 10-féle bizonyítása és 3-féle általánosítása van. A megoldási módszerek az érdekesek és tanulságosak.
Amúgy pedig a (b) változatra is gondolkodás nélkül alkalmazhatnánk az új változók bevezetését, csak bonyolult lenne.
|
| Előzmény: [3690] Fálesz Mihály, 2013-02-20 18:56:28 |
|
| [3690] Fálesz Mihály | 2013-02-20 18:56:28 |
 Hát, alaposan túlbonyolítottátok.
Jól ismert, hogy a terület és a (fél)kerület(négyzet) összehasonlításához az (s-a), (s-b) és (s-c) számok számtani és mértani közepeit érdemes venni:
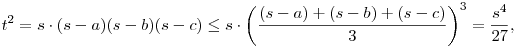
tehát 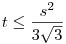 , egyenlőség csak s-a=s-b=s-c, vagyis szabályos háromszögre. , egyenlőség csak s-a=s-b=s-c, vagyis szabályos háromszögre.
Ha az oldalak négyzetösszege kell, akkor ezután jöhet a számtani-négyzetes az oldalakra.
(Csak tudnám, hogy ez az egyenlőtlenség miért "érdekes"...)
|
| Előzmény: [3689] w, 2013-02-20 10:54:27 |
|
| [3689] w | 2013-02-20 10:54:27 |
 Nem lövök le túl sokat, ha elmondom: az (a) részt a Róbert Gida által mondott módszerrel könnyebben meg lehet oldani, mint az eredetit, ujjgyakorlat. Átrendezve:
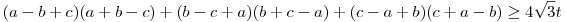 . .
Legyen x=-a+b+c, y=a-b+c, z=a+b-c, a Hérón-képlet miatt:
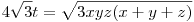 . Átírva az egyenlőtlenséget: . Átírva az egyenlőtlenséget:
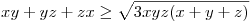
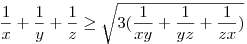
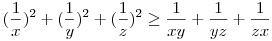 ismert, ekv. átalakítások miatt az eredeti is igaz. ismert, ekv. átalakítások miatt az eredeti is igaz.
|
| Előzmény: [3688] w, 2013-02-20 07:52:28 |
|
|
| [3687] Róbert Gida | 2013-02-19 21:46:12 |
 Nagyon ismerősnek tűnik. Gondolkodás nélkül: ha a,b,c egy háromszög oldalai, akkor a=y+z,b=x+z,c=x+y, ahol x=s-a,y=s-b,z=s-c és x,y,z>0 és ez visszafelé is igaz, ez nagyon hasznos az összes ilyen tipusú feladatnál, a háromszög kilőve. Héron képlettel: 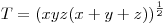 . Ezt beírva és négyzetre emelve a két oldalt és rendezve a bizonyítandó: . Ezt beírva és négyzetre emelve a két oldalt és rendezve a bizonyítandó: 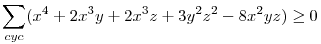 , ez pedig a számtani-mértani miatt igaz, az is látszik, hogy egyenlőség pontosan akkor van, ha x=y=z, azaz szabályos háromszögnél. , ez pedig a számtani-mértani miatt igaz, az is látszik, hogy egyenlőség pontosan akkor van, ha x=y=z, azaz szabályos háromszögnél.
|
| Előzmény: [3686] w, 2013-02-19 19:37:40 |
|
| [3686] w | 2013-02-19 19:37:40 |
 Adott egy háromszög, oldalai: a, b, c; területe t. Igazoljuk:
 . .
|
|
| [3685] jenei.attila | 2013-02-19 12:10:49 |
 Megnéztem a megoldást, szerintem a két konstrukció hasonló elvű, csak az enyém egyszerűbb. Egyébként először én is ezt a "hivatalos" megoldást adtam meg, és azután egyszerűsítettem.
|
| Előzmény: [3684] m2mm, 2013-02-19 00:26:45 |
|
| [3684] m2mm | 2013-02-19 00:26:45 |
 1 megoldásra emlékszem, az a hivatalos, megtalálható a 3681 hozzászólás linkjében. És igen, RMM a mostani hiv. név, régen volt ez RMMS, nekünk RMMC(C for competition) néven volt ismert.
|
| Előzmény: [3683] jenei.attila, 2013-02-16 08:42:56 |
|
|
|
|
|
| [3679] jenei.attila | 2013-02-15 08:30:10 |
 Ezt nem tudtam, de aki ismeri vagy megoldotta, azzal megbeszélhetjük. Az én megoldásom:
f(x)=(-1)[x]xhax>0
f(0)=0
f(x)=-f(-x)hax<0
g(x)=(-1)[x](x+1)hax>0
g(0)=0
g(x)=-g(-x)hax<0
|
| Előzmény: [3678] m2mm, 2013-02-15 05:05:37 |
|
|
|
| [3676] jenei.attila | 2013-02-14 21:09:19 |
 Képlettel:
(1*9+2*8+3*7+4*6+5*5+6*4+7*3+8*2+9*1)*20/4
Ez a következőképpen jön ki: a pontokat számozzuk 1-től 20-ig a körvonalon egymás után. Az első kiválasztott pont legyen az 1-es. Ekkor a 3-adik kiválasztott pont (körbehaladva számozva)7-estől 15-ösig lehet. Ha a 7-es a 3.-adik kiválasztott pont, akkor a 2. kiválasztott csak a 4-es lehet, a 4.-edik kiválasztott pedig 10-estől 18-asig 9 féle lehet. Ha 8-as a 3. kiválasztott pont, akkor a 2. kiválasztott 4-es és 5-ös lehet, a 4. kiválasztott 11-18-ig mehet. És így tovább: az 1. kiválasztott pont rögzítése mellet
1*9+2*8+3*7+4*6+5*5+6*4+7*3+8*2+9*1
jó kiválasztás létezik. Az 1. kiválasztott pontot 20 féleképpen rögzíthetjük, vagyis a jó kiválasztásokat úgy számolhatjuk össze, hogy a most kapott értéket 20-szal szorozzuk, de akkor minden egyes kiválasztást 4-szer számolunk, hiszen bármelyik pontját tekinthetjük 1. kiválasztott pontnak.
|
| Előzmény: [3675] Róbert Gida, 2013-02-14 18:55:51 |
|
|
| [3674] jenei.attila | 2013-02-14 09:43:24 |
 Adott a körvonalon 20 pont. Hányféleképpen választható ki ezek közül 4 pont úgy, hogy bármely két kiválasztott pont között legalább két ki nem választott pont fekszik. Erre a feladatra válaszoltam, ha jól értettem az angol szöveget. Tehát a válasz 825. Legalábbis szerintem. Szerintetek?
|
| Előzmény: [3673] jenei.attila, 2013-02-11 11:04:24 |
|
|
|
| [3671] juantheron | 2013-02-08 06:41:53 |
 There are 20 points in a circle A1,A2,...A20.
Find the number of ways of selecting 4 points such that
there are at-least two points in between any two selected
points.
|
|
| [3670] w | 2013-02-05 16:59:02 |
 Nem sokan foglalkoztak a feladattal, elmondom a megoldást. Legyen 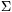 si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy
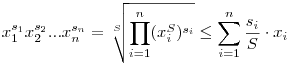 , ,
ahol a súlyozott mértani és számtani közép egyenlőtlenségét használtuk ki. Mindegyik tagot a jobb oldalon hasonlóan megbecsülve, majd az egyenlőtlenségeket összegezve a bizonyítandó adódik, hiszen az egyes xi számok előtt minden lehetséges 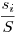 szorzótényező szerepel, és ezek összege 1. szorzótényező szerepel, és ezek összege 1.
|
| Előzmény: [3649] w, 2013-01-13 21:25:23 |
|
| [3669] jenei.attila | 2013-02-05 14:34:25 |
 Egy érdekes feladat: Léteznek-e f:R->R és g:R->R függvények úgy, hogy x->g(f(x)) szigorúan monoton növő, x->f(g(x)) pedig szigorúan monoton fogyó.
|
|
| [3668] marcius8 | 2013-02-04 15:48:49 |
 Tisztelt Látogatók!
Egy játékot találtam ki. Mivel egy játékkal akkor foglalkoznak sokan, ha szabályai egyszerűek, ugyanakkor nem könnyen végigjátszható, ezért a következő játékot találtam ki:
A magyar kártyacsomag összetétele: A magyar kártyacsomag 32 lapot tartalmaz. Minden lapnak van színe és értéke. A színek lehetnek: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél). Az értékek lehetnek: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”. A kártyacsomagban minden lehetséges szín-érték párosítás előfordul.
A nyolc sorból és négy oszlopból álló táblázatban elhelyezett magyar kártyacsomag lapjai akkor vannak rendezett sorrendben, ha a következő feltételek teljesülnek:
• A táblázat minden oszlopában található négy lap színének sorrendje felülről lefelé haladva: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél).
• A táblázat minden sorában található nyolc lap értékének sorrendje balról jobbra haladva: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”.
A játék szabálya: A kártyacsomag lapjai véletlenszerű sorrendben egy négy sorból és nyolc oszlopból álló táblázatban vannak elhelyezve. A játék során egyszerre mindig két lapot lehet megcserélni. Két lapot csak akkor lehet megcserélni, ha a két lap ugyanabban a sorban vagy ugyanabban az oszlopban van, továbbá (és) ha a két lap színe vagy értéke ugyanaz. A játék célja, hogy a kártyalapok sorrendje rendezett legyen.
Az érdekes az hogy a véletlenszerűen összekevert állapotból majdnem mindig abba az állapotba jutok, hogy a rendezett állapothoz képest a "makk ász" és a "tök király" fel van cserélve. Sajnos, nem tudok rájönni, hogy ez az én ügyetlenségem (gyanítom, hogy igen), de ugyanakkor nem hiszem hogy ennek törvényszerűen így kell lenni. Arra kérek bárkit, hogy ha ezt a jelenséget meg tudja indokolni, vagy meg tudja oldani (tehát ha a rendezett állapothoz képest csak a "makk ász" és a "tök király" van felcserélve, akkor ez az állapot rendezhető vagy sem), írjon a marcius.08@freemail.hu címre.
|
|
|
| [3666] ibiro | 2013-02-02 21:00:07 |
 Sajnos nem értem melyik jobb oldalra gondolsz, a [3649]-ben ? És miért a negyedik hatványra ? Még nincs bizonyitva hogy a [3652] igaz n-re is !
|
| Előzmény: [3665] w, 2013-02-01 19:25:15 |
|
|
| [3664] Róbert Gida | 2013-02-01 01:02:20 |
 Helyes. A módszerről, amivel ezt polinom időben meg lehet kapni: http://en.wikipedia.org/wiki/Modular_exponentiation Right-to-left binary method bekezdése. 3123456789123456789 utolsó 20 számjegye éppen a hatvány m=1020-al vett osztási maradéka amit 1 ezredmásodpercbe sem telik kiszámolni egy átlagos gépen.
Enélkül például az RSA sem lenne gyors, így nagyon fontos ez a módszer, http://en.wikipedia.org/wiki/RSA_(algorithm)
|
| Előzmény: [3663] jonas, 2013-01-31 23:47:10 |
|
|
| [3662] w | 2013-01-31 21:17:18 |
 Nem tudok programozni, de gondolom, sok időbe tartana megkeresni a 20 jegyet. Brutális magasságokba szárnyalhat a periódus hossza, az általad említett példában nem is biztos, hogy lesz 123456789123456789-ig valamilyen periódus (akár 4.1019 hosszú is lehetne). Köszönöm a hozzászólást, ebben tévedtem, mert 4545 utolsó négy számjegye is talán az első periódusban van. Amúgy általában az a tapasztalat, hogy a periódus a becsültnél sokkal rövidebb (persze akkor, ha maximumot becslünk :) ), erről ki is lehetne dolgozni egy kisebb elméletet... De egyenlőre ez engem nem izgat.
|
| Előzmény: [3661] Róbert Gida, 2013-01-31 20:59:37 |
|
|
|
|
| [3658] w | 2013-01-31 19:21:02 |
 Minden bizonnyal a Te megoldásod a legelegánsabb, mert direkt úton visszavezeti a teljes négyzet-egyenlőtlenségre. Helyette próbáld a közepek közötti egyenlőtlenségekkel igazolni a feladatot (természetesebb is az adható megoldás).
Persze rendezési tétellel azonnal látszik ennek a megoldása, de nem működik az általános verzióra határértékek nélkül.
|
| Előzmény: [3653] ibiro, 2013-01-31 13:48:15 |
|
| [3657] w | 2013-01-31 19:16:02 |
 Lehet, hogy van rá egyszerűbb okoskodás, de az utolsó négy számjegyet a hatványok utolsó n számjegyének periodikus ismétlődésével meghatározhatjuk (ezt a 4545-re használjuk, az 5454 meg számológéppel megadható).
|
| Előzmény: [3654] Hajba Károly, 2013-01-31 17:14:38 |
|
|
|
|
| [3653] ibiro | 2013-01-31 13:48:15 |
 Kezdetnek nem rossz, de engem legalábbis nem visz közelebb az általánosabb megoldáshoz, megszorozzuk 4-el mindkét oldalt majd ilyen alakba lehet írni : 2(a2-bc)2+2(b2-ac)2+2(c2-ab)2+(a2-b2)2+(b2-c2)2+(c2-a2)2>=0
|
| Előzmény: [3652] w, 2013-01-30 17:26:13 |
|
| [3652] w | 2013-01-30 17:26:13 |
 Kezdésképpen igazoljuk, hogy
a4+b4+c4 a2bc+b2ca+c2ab. a2bc+b2ca+c2ab.
|
|
|
| [3650] ibiro | 2013-01-30 13:30:19 |
 A "tetszőleges xi>0, si valós számokra" kifejezés azt jelenti hogy si>0 ??? Ha igen akkor lehet gondolkozni a feladaton, ha pedig lehetnek negatív számok is, akkor nem igaz az egyenlőtlenség: n=2, x1=1, x2=2, s1=2,s2=-1 .
|
| Előzmény: [3649] w, 2013-01-13 21:25:23 |
|
| [3649] w | 2013-01-13 21:25:23 |
 Mutassuk meg, hogy tetszőleges xi>0, si valós számokra fennáll (i=1, 2, ..., n):
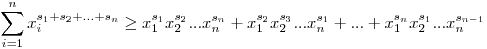 . .
|
|
| [3648] ibiro | 2012-12-08 22:26:04 |
 Az algoritmus remek és tényleg megérti egy hetedikes is, de biztos nem igy kapjuk meg a legkevesebb számú lépést (12,36,324,26244,26243,...,2012) és az algoritmus szerint ez az egyetlen megoldás, a valóságban pedig több is van.
|
| Előzmény: [3647] w, 2012-12-08 21:14:42 |
|
| [3647] w | 2012-12-08 21:14:42 |
 Mi választjuk-e meg a-t és b-t?
Erre egy trviális algoritmus: páros n=2k-ból k2 képezhető, ahol k2>2k, ha (k-1)2>1, k>2, n>4; páratlan n=2k+1-ből k(k+1) képezhető, itt k(k+1)=k2+k>2k+1, ha 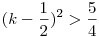 , , 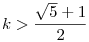 , , 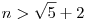 . Tehát szig. mon. növ. sorozatot képezhetünk n0>4 esetén, végül n=n-1+1 -ből n-1 képezhető, elég nagy sorozattag választásával így lecsökkenthetünk a szükséges számra. N>4-re tetszőleges M elérhető, de az is látszik, hogy N . Tehát szig. mon. növ. sorozatot képezhetünk n0>4 esetén, végül n=n-1+1 -ből n-1 képezhető, elég nagy sorozattag választásával így lecsökkenthetünk a szükséges számra. N>4-re tetszőleges M elérhető, de az is látszik, hogy N 4 esetén csak M 4 esetén csak M N érhető el. N érhető el.
Ilyen módon ez könnyen hetedikes szint. A megoldások és lépések minimális száma nem ilyen egyszerű, finoman fogalmazva.
|
| Előzmény: [3645] ibiro, 2012-12-08 11:45:22 |
|



 b4 (mod n). Ezt pedig visszahatványozva adódik, hogy n|a100+b100
b4 (mod n). Ezt pedig visszahatványozva adódik, hogy n|a100+b100





 deriválás... :-)
deriválás... :-)  R függvényt, melyre f(x)2=1 teljesül minden x-re.
R függvényt, melyre f(x)2=1 teljesül minden x-re.
 64-re
64-re  n1/2 igaz minden k
n1/2 igaz minden k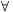
 ,
, >0
>0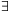 k0, hogy k>k0 esetén:
k0, hogy k>k0 esetén: 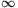 , ha An={ai|ai<n}
, ha An={ai|ai<n}  1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint
1 (mod 73). Vegyük észre, hogy 20=7k-1 alakú, ezért a binomiális tétel szerint  +1 alakú, ahol
+1 alakú, ahol 


 tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy
tranformációt, melyben minden Pi pont képe egy olyan Pi' pont lesz, hogy a parabolának minden olyan húrjának, amelynek a felezőmerőlegese átment Pi-n, a képe egy olyan húr, amelynek a felezőmerőlegese átmegy Pi'-n. Bizonyítsd be, hogy 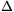 szabályos, így BP0C
szabályos, így BP0C =120o és BP0’A’
=120o és BP0’A’
 szám kell nekünk, melyre az
szám kell nekünk, melyre az  (-1;+1) esetén következik be, és ekkor
(-1;+1) esetén következik be, és ekkor 

 Lmin(H,S)?
Lmin(H,S)?  (k) a híres Riemann-féle zéta-függvény. Riasztóbb, mint amilyen.
(k) a híres Riemann-féle zéta-függvény. Riasztóbb, mint amilyen.  A2
A2


 si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy
si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy 
