| [1428] phantom_of_the_opera | 2006-10-21 23:10:52 |
 Megint én.
A következő feladat okoz igen nagy gondot:
Bizonyítsuk be, hogy 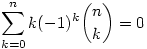 . Egyébként n . Egyébként n 2-től igaz csak... 2-től igaz csak...
Állítólag indukcióval kéne, addig jutok, hogy megpróbálom párosítani a szélső tagokat, hogy bele lehessen keverni a binomiális tételt, de igen körülményes, és máshogy se akar kijönni. Tudnátok segíteni?
Előre is köszönöm.
(Lóczi Lajos: ha kapok rá plusz pontot, ha nem, megőrülök hogy nem tudom megcsinálni és nem bírom ki a következő gyakig (nov 6))
|
|
|
|
|
| [1432] nadorp | 2006-10-22 22:55:30 |
 Kedves phantom_of_the_opera !
Utólag olvasva [1429] hozzászólásod végét, nem volt "szép dolog" Lóczi Lajossal szemben, hogy megoldottuk a szorgalmi példádat. Álljon itt egy hasonló, hátha mégis kaphatsz plusz pontot :-)
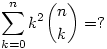
|
| Előzmény: [1431] phantom_of_the_opera, 2006-10-22 14:04:51 |
|
|
| [1434] djlado | 2006-10-24 08:31:04 |
 Erdekes feladat:
Hogyan visz ki a pincerno 20 palinkat 5x re ugy , hogy mind az 5x parantlant vigyen?
|
|
|
|
|
|
|
|
|
| [1442] Cckek | 2006-10-27 22:25:21 |
 A következő érdekes azonosság, permutációk fixpontjainak a kiszámolásánál jött elő:

Lehet adni rá egy egyszerű bizonyítást?
|
|
|
|
|
|
| [1447] nadorp | 2006-10-29 01:29:11 |
 A szita formula egy ismert alkalmazása a következő: Egy színházi előadáson a ruhatárba n darab ernyőt adtak le. Az előadás után senki sem a saját ernyőjét kapta meg. Hányféleképpen történhet meg ez ?
Az eredmény 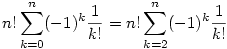
A fenti alapján az 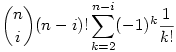 képlet az (1,2,...n) azon permutációinak a száma, amikor pontosan i darab elem van a saját helyén. Ha i=n-1, akkor az összeg 0, hiszen nincs olyan eset, amikor n-1 elem a saját helyén van és 1 meg nem. Ha i=n, a kkor a fenti összeg 1, hiszen minden elem a saját helyén van. Az összes esetek száma az n darab elem permutációinak a száma, azaz n!. Tehát képlet az (1,2,...n) azon permutációinak a száma, amikor pontosan i darab elem van a saját helyén. Ha i=n-1, akkor az összeg 0, hiszen nincs olyan eset, amikor n-1 elem a saját helyén van és 1 meg nem. Ha i=n, a kkor a fenti összeg 1, hiszen minden elem a saját helyén van. Az összes esetek száma az n darab elem permutációinak a száma, azaz n!. Tehát
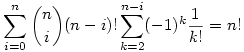
|
| Előzmény: [1442] Cckek, 2006-10-27 22:25:21 |
|
| [1448] Cckek | 2006-10-29 07:55:26 |
 Nos, nagyon szép bizonyítás, a képletek levezetése nekekem napokba telt.Egy kis korekció, remélem nem fogsz megsértődni érte, az első szumma nem mehet n-ig: 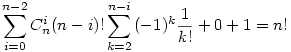
Ahol 0 az n-1 fixponttal rendelkező permutációk száma-tudjuk, hogy ilyen nincs:), 1 az n fixpontal rendelkező permutációk száma, tudjuk hogy ilyen csak egy van az identikus permutáció. Amúgy találtam rá egy egyszerű bizonyítást:
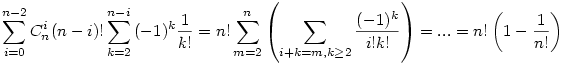
|
| Előzmény: [1447] nadorp, 2006-10-29 01:29:11 |
|
|
| [1450] Cckek | 2006-10-29 18:41:57 |
 A következő "differenciálegyenlethez" kellene egy kis segítség: 2xf'(x)=f(2x). Az f(x)=ax illetve f(x)=ax2 függvények megoldások. Van más is?
|
|
|
| [1453] Cckek | 2006-10-30 14:19:43 |
 Ez egy nagyon érdekes következtetés. Ugyanis én valójában az (x+y)(f(x)-f(y))=(x-y)f(x+y)funkcionálegyenletet alakítottam-nem egészen ortodox módon:)-ezzé a differenciálegyenletté. S valóban ennek a funkcionálegyenletnek ezek a függvények a megoldásai.Hogy van-e más is? Jó kérdés:)
|
| Előzmény: [1451] nadorp, 2006-10-30 08:56:12 |
|
| [1454] Yegreg | 2006-10-30 23:56:41 |
 Nem kapcsolódik az aktuális témához, de itt kérdezem meg:
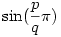 mikor írható fel egész számokkal, alapműveletek és gyökök segítségével? (amúgy elvileg mindig algebrai) mikor írható fel egész számokkal, alapműveletek és gyökök segítségével? (amúgy elvileg mindig algebrai)
Pl: 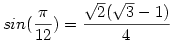
|
|
| [1455] nadorp | 2006-10-31 09:23:17 |
 Ha f(x)=xg(x), akkor
xg(x)-yg(y)=(x-y)g(x+y)
Azaz tetszőleges t-vel
(x+t)g(x+t)-xg(x)=t.g(2x+t) és
xg(x)-(x-t)g(x-t)=t.g(2x-t) Összeadva
(x+t)g(x+t)-(x-t)g(x-t)=t(g(2x+t)+g(2x-t)) A baloldalra újra alkalmazva az eredeti egyenlőséget:
2t.g(2x)=t(g(2x+t)+g(2x-t)) Bevezetve a 2x+t=p, 2x-t=q jelölést
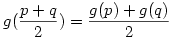 minden p,q valós számra. Ebből úgy néz ki, hogy a függvény konvex és konkáv egyszerre, azaz valószínűleg egyenes. Ha viszont g(x) egyenes, akkor f(x) csak a már megtalált megoldás lehet. minden p,q valós számra. Ebből úgy néz ki, hogy a függvény konvex és konkáv egyszerre, azaz valószínűleg egyenes. Ha viszont g(x) egyenes, akkor f(x) csak a már megtalált megoldás lehet.
|
| Előzmény: [1453] Cckek, 2006-10-30 14:19:43 |
|
| [1456] Lóczi Lajos | 2006-10-31 09:43:51 |
 Persze ennek a függvényegyenletnek lehet, hogy vannak nemfolytonos, s így nemderiválható megoldásai is, ami lehetetlenné teszi az összes megoldás explicit felírását. (Analógia alapján, a Cauchy-féle f(x+y)=f(x)+f(y) egyenletről jutott eszembe, aminek "csúnya" megoldásából meglehetősen "sok" van.)
|
| Előzmény: [1453] Cckek, 2006-10-30 14:19:43 |
|
|
|
|
| [1460] nadorp | 2006-10-31 10:41:56 |
 És mi a helyzet a 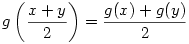 függvényegyenlettel. Feltesszük, hogy pld. x,y>0 ( ez az előző hozzászólásom hiányossága, mert nem zártam ki az x+y=0 lehetőséget az eredeti függvényegyenlet átalakításakor). Van ennek "csúnya" megoldása ? függvényegyenlettel. Feltesszük, hogy pld. x,y>0 ( ez az előző hozzászólásom hiányossága, mert nem zártam ki az x+y=0 lehetőséget az eredeti függvényegyenlet átalakításakor). Van ennek "csúnya" megoldása ?
|
| Előzmény: [1456] Lóczi Lajos, 2006-10-31 09:43:51 |
|
|
| [1462] Lóczi Lajos | 2006-10-31 11:51:03 |
 A választ Aczél János vagy Kuczma klasszikus függvényegyenletes könyvei bizonyára tartalmazzák. Az egyenlet neve egyébként Jensen-függvényegyenlet, érdemes megnézni, a neten erről van-e vmi "discontinuous" vagy "nowhere continuous" link, én konkrétat ezalatt a kis idő alatt nem találtam, talán azért, mert a kérdés nagyon klasszikus ízű. Intuitíve biztos vagyok benne, hogy ennek is van millió más megoldása. A konstrukció nyilván Hamel-bázissal kell történjen, a Cauchy-egyenlet mintájára. A megoldásfüggvények grafikonjai ilyen esetben az egész síkon sűrű ponthalmazok szoktak lenni.
|
| Előzmény: [1460] nadorp, 2006-10-31 10:41:56 |
|
|
| [1464] Lóczi Lajos | 2006-10-31 14:44:53 |
 Igen, a debreceni KLTE-s PDF szép leírás.
Még egy dolog eszembe jutott, már egyszer volt is szó róla itt a fórumon, a hatványsoros megközelítéssel kapcsolatban: tudjuk, hogy vannak 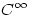 , de nem , de nem 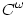 függvények, vagyis olyan függvények, amelyek akárhányszor deriválhatók ugyan, de nem analitikusak, azaz nem fejthetők Taylor-sorba. függvények, vagyis olyan függvények, amelyek akárhányszor deriválhatók ugyan, de nem analitikusak, azaz nem fejthetők Taylor-sorba.
Egy ilyen függvény pl. az f(x):=e-1/x2, ha x 0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem. 0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem.
Szóval elvileg ilyen megoldása is lehet egy függvényegyenletnek, ezeket tehát hatványsorfejtéssel nem lehet megtalálni, noha a folytonossággal/deriválhatósággal nincs baj.
|
| Előzmény: [1451] nadorp, 2006-10-30 08:56:12 |
|
| [1465] Cckek | 2006-10-31 19:52:14 |
 Nos, én is utánnaolvasgattam, úgy tűnik a Jensen egyenlet megoldásai A(x)+a alakúak, ahol A(x) a Cauchy egyenlet megoldása, s mint ilyen lehet nemfolytonos is. Mindenesetre mindkettőtöknek köszönöm a segítségét, megint bebizonyosodott milyen könnyű függvényegyenletet szerkeszteni és milyen nehéz őket megoldani:).
|
| Előzmény: [1462] Lóczi Lajos, 2006-10-31 11:51:03 |
|
| [1466] Lóczi Lajos | 2006-10-31 21:07:22 |
 Egy jópofa feladat:
Adott  valós szám esetén számítsuk ki a valós szám esetén számítsuk ki a 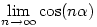 határértéket. határértéket.
|
|
| [1467] Lóczi Lajos | 2006-10-31 21:50:29 |
 Adjuk meg mindazokat az x>0 valós számokat, melyekre fennáll, hogy
xx2+1=e1-x3.
|
|
|
|
|
|
|
|
|
|
|
| [1477] Python | 2006-11-01 15:17:36 |
 Bemutatkozásul egy, feladat, ma olvatam:
238. feladat Gondoltam egy törtre, a számlálója és a nevezője is kétjegyű. A számlálónak és a nevezőnek egy-egy jegyét elhagyva (pl.: 56-ból a hatost elhagyva 5-öt kapunk) a tört egyszerűsített alakját kapjuk. Melyik lehet ez a tört?
Meg egy saját:
239. feladat
Négyzetrácsos terepen él a matekkígyó. A négyzetrács minden mezőjén vagy nincs semmi, vagy élelem van, vagy fal, vagy a kígyó feje, vagy a kígyó testének egy szakasza. A kígyó (nem sárkány, így a) testén nincs elágazás. Egy időegységen belül:
I. Ha nincs élelem a terepen, valahonnan egy véletlenszerűen kiválasztódott üres mezőre egy adag élelem kerül.
II. Mozog a kígyó:
1. A kígyó feje elmozdul egy oldalszomszédos mezőre, amelyen élelem van. Ekkor a kígyó feje helyén testszakasz jelenik meg, nyúlik a kígyó.
2. A kígyó feje elmozdul egy oldalszomszédos üres mezőre. Ekkor mozog, minden testszakasza előrébb mozdul, az utolsó helyén üres hely alakul ki.
3. Ha nem tud mozogni (1. v. 2.), rövidül, elveszti az utolsó testtáját.
a) Egy ilyen terepen:
| # |
# |
# |
# |
| # |
|
|
# |
| # |
:) |
|
# |
| # |
# |
# |
# |
|
, ahol '#'=fal; ':)'=kígyó feje; ' '(space)=üres mező (A kígyónak még nincs teste, de tfh túléli...) elérheti-e a kígyó a 3 testszakasz+fej hosszt, és ha igen, optimális stratégia mellett legfeljebb hány időegység alatt? (Hányadik időegység végére eszi meg az utolsó élelmet?)
b) Terep:
| # |
# |
# |
# |
# |
| # |
# |
|
# |
# |
| # |
|
:) |
|
# |
| # |
# |
|
# |
# |
| # |
# |
# |
# |
# |
|
Kérdés ugyanaz, de itt csak 2 testszakasz+fej kell.
|
|
| [1478] jonas | 2006-11-01 17:45:29 |
 238. Ez a feladat azért nem jó, mert túl sok megoldása van. Mondj még valami információt, különben nem tudunk választani.
A lehetséges megoldások:
20/10=2/1, 22/11=2/1, 24/12=2/1, 24/12=4/2, 26/13=2/1, 26/13=6/3, 28/14=2/1, 28/14=8/4, 30/10=3/1, 30/20=3/2, 32/16=2/1, 33/11=3/1, 33/22=3/2, 36/12=3/1, 36/12=6/2, 36/24=3/2, 36/24=6/4, 39/13=3/1, 39/13=9/3, 39/26=3/2, 39/26=9/6, 40/10=4/1, 40/20=4/2, 40/30=4/3, 42/21=4/2, 42/21=2/1, 44/11=4/1, 44/22=4/2, 44/33=4/3, 46/23=4/2, 46/23=6/3, 48/12=4/1, 48/12=8/2, 48/24=4/2, 48/24=8/4, 48/36=4/3, 48/36=8/6, 50/10=5/1, 50/20=5/2, 50/30=5/3, 50/40=5/4, 54/27=4/2, 55/11=5/1, 55/22=5/2, 55/33=5/3, 55/44=5/4, 60/10=6/1, 60/20=6/2, 60/30=6/3, 60/40=6/4, 60/50=6/5, 62/31=6/3, 62/31=2/1, 63/21=6/2, 63/21=3/1, 63/42=6/4, 63/42=3/2, 64/16=4/1, 64/32=6/3, 64/32=4/2, 65/13=5/1, 65/26=5/2, 65/39=5/3, 66/11=6/1, 66/22=6/2, 66/33=6/3, 66/44=6/4, 66/55=6/5, 68/34=6/3, 68/34=8/4, 69/23=6/2, 69/23=9/3, 69/46=6/4, 69/46=9/6, 70/10=7/1, 70/20=7/2, 70/30=7/3, 70/40=7/4, 70/50=7/5, 70/60=7/6, 75/15=5/1, 76/38=6/3, 77/11=7/1, 77/22=7/2, 77/33=7/3, 77/44=7/4, 77/55=7/5, 77/66=7/6, 80/10=8/1, 80/20=8/2, 80/30=8/3, 80/40=8/4, 80/50=8/5, 80/60=8/6, 80/70=8/7, 82/41=8/4, 82/41=2/1, 84/21=8/2, 84/21=4/1, 84/42=8/4, 84/42=4/2, 84/63=8/6, 84/63=4/3, 85/17=5/1, 86/43=8/4, 86/43=6/3, 88/11=8/1, 88/22=8/2, 88/33=8/3, 88/44=8/4, 88/55=8/5, 88/66=8/6, 88/77=8/7, 90/10=9/1, 90/20=9/2, 90/30=9/3, 90/40=9/4, 90/50=9/5, 90/60=9/6, 90/70=9/7, 90/80=9/8, 93/31=9/3, 93/31=3/1, 93/62=9/6, 93/62=3/2, 95/19=5/1, 96/16=6/1, 96/32=9/3, 96/32=6/2, 96/64=9/6, 96/64=6/4, 98/49=8/4, 99/11=9/1, 99/22=9/2, 99/33=9/3, 99/44=9/4, 99/55=9/5, 99/66=9/6, 99/77=9/7, 99/88=9/8,
Ezen kívül mindegyik megoldás úgy is, ha a számlálókat és nevezőket felcseréljük, van továbbá egy csomó olyan megoldás is, amikor a számláló egyenlő a nevezővel.
|
| Előzmény: [1477] Python, 2006-11-01 15:17:36 |
|
|
|
| [1481] jonas | 2006-11-01 21:47:32 |
 Valóban. Így még mindig van egy csomó olyan, mint 38/38=3/3 meg olyan hogy 30/70=3/7. Ha ezeket leszámítjuk, akkor tényleg csak ez a négy megoldás van, meg uganezek fejenállva.
|
| Előzmény: [1479] Python, 2006-11-01 18:51:05 |
|
| [1482] kdano | 2006-11-01 22:04:15 |
 Hát igen, ha kikötjük, hogy a tört értéke kisebb, mint egy, s a letörlendő számjegyek pozitívak, akkor kész vagyunk, a feladat megfogalmazását befejeztük :D
|
| Előzmény: [1481] jonas, 2006-11-01 21:47:32 |
|
| [1483] Python | 2006-11-02 16:46:02 |
 240.feladat
Ezeken a számológépgombkon beütünk egy tízjegyű számot (x) úgy, hogy minden jegye pontosan egyszer szerepel, és két egymás utáni jegy gombja oldalszomszédos (tehát pl.: 7 előtt/után lehet 4 vagy 8).
a)Hányféleképpen üthetjük be?
b)Mennyi sin xo (x fok szinusza)?
|
|
| [1484] tommyk | 2006-11-05 09:53:33 |
 Sziasztok!
Van egy feladat ,melyhez kérném a segítségeteket! A feladat a következő: Van egy pásztor, annak meg van egy tökéletesen kör alakú mezeje K1 sugarú. A mi pásztorunk megegyezik a szomszéd pásztorral, hogy használhatja az ő mezejét. A szomszéd pásztor egyetlen egy birkát legeltethet ezen a kör alakú mezőn úgy, hogy annak PONTOSAN csak a felét eheti meg a birka. Továbbá a birka csak a körmező szélén egy póznához kikötve mozoghat. Kérdés: mekkora sugarú körön K2 kell mozogni a birkának ahhoz, hogy pontosan a felét legelje le a körmezőnek? K1/K2=?
|
|
|
|
|
|
| [1489] Cckek | 2006-11-11 13:10:18 |
 Nagyon érdekes kis határértékfeladat:)
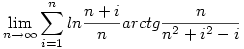
|
|
| [1490] jenei.attila | 2006-11-12 22:21:29 |
 Egy kis segítség kéne. Szerintem egy határozott integrál közelítő összege lehet, mégpedig az ln függvény Stieltjes integrálja az [1,2] intervallumon (n egyenlő részre osztva az intervallumot), ami szerint pedig a Stieltjes integrált képezzük, egy olyan g függvény, amelyre g(1+i/n)-g(1+(i-1)/n)=arctg(...).
|
| Előzmény: [1489] Cckek, 2006-11-11 13:10:18 |
|
|
|
|
|
|
| [1496] jenei.attila | 2006-11-13 13:54:16 |
 Szép megoldás, de most már kíváncsi lennék, Cckek szerint mitől is olyan érdekes ez a feladat. Nekem inkább kissé mesterkéltnek és "strapásnak" tűnik, hacsak nincs rá egy ettől különböző igazán szellemes megoldás.
|
| Előzmény: [1495] nadorp, 2006-11-13 13:31:54 |
|
|
| [1498] Cckek | 2006-11-13 18:16:57 |
 Nos a feladat két okból is nagyon érdekes:)) Először mert az én szerzeményem:)), másodszor mert senki sem ismerte fel még - és ezt komolyan mondom-a nagyrabecsült jelenlévők közül sem hogy ez valójában egy Riemann összeg, mégpedig az
![f:[0,\frac{\pi}{4}]\to R, f(x)=ln(1+tgx)](keplet.cgi?k=E93A7EC15B68CCE4)
függvény es a
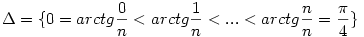 felosztáshoz rendelt Riemann integrálösszeg.Tehát egyenlő a felosztáshoz rendelt Riemann integrálösszeg.Tehát egyenlő a 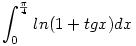 integrállal. integrállal.
|
| Előzmény: [1496] jenei.attila, 2006-11-13 13:54:16 |
|
| [1499] Cckek | 2006-11-13 18:25:05 |
 Ami mellesleg egy jólismert cseles integrál :) az 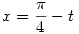 helyetesítéssel kiszámítható, és kitűnő példa olyan függvény integráljának a kiszámítására amelyenk nem ismerjük a primitív függvényét:)) helyetesítéssel kiszámítható, és kitűnő példa olyan függvény integráljának a kiszámítására amelyenk nem ismerjük a primitív függvényét:))
|
| Előzmény: [1498] Cckek, 2006-11-13 18:16:57 |
|
| [1500] Cckek | 2006-11-13 18:37:41 |
 Amúgy a feladat főleg középiskolásoknak szól, itt csak azárt tűztem ki, mert már megjelent egy Erdély-i matematikai folyóiratban a MATLAP-ban, és nagyon kevés helyes megoldás érkezett:))
|
| Előzmény: [1499] Cckek, 2006-11-13 18:25:05 |
|
|
|
|
| [1504] jenei.attila | 2006-11-14 11:32:30 |
 Kedves Cckek!
Először is maradjunk annyiban, tényleg érdekes a feladatot, csak kicsit másra számítottam. Másrészt nem egészen értem, mit is nem ismertünk fel? Azt, hogy Riemann-Stieltjes integrál közelítő összeg, észrevettük. Nadorp pedig megoldotta az integrálást, vagyis a feladat ezzel megoldódott.
|
| Előzmény: [1498] Cckek, 2006-11-13 18:16:57 |
|
|
| [1506] nadorp | 2006-11-14 12:19:34 |
 Szerintem Cckek arra gondol, hogy kár belekeverni a példába a Stieltjes-integrált, mert ha az eredeti szummában észrevesszük a 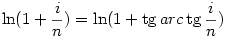 nyilvánvaló összefüggést, akkor mezei Riemann közelítő összeget kapunk, és azonnal adódik a nálam az x=tg y helyettesítés után kapott integrál. nyilvánvaló összefüggést, akkor mezei Riemann közelítő összeget kapunk, és azonnal adódik a nálam az x=tg y helyettesítés után kapott integrál.
|
| Előzmény: [1505] Sirpi, 2006-11-14 11:40:26 |
|
| [1507] jenei.attila | 2006-11-14 12:25:38 |
 Lehet, hogy erre gondolt, de ez szerintem kb. ugyanaz mint a stieltjes integrál, csak nem nevezzük nevén. Egyébként gondolom Te már előttem felismerted az integrál közelítő összeget. Te nem Stieltjes integrálra gondoltál?
|
| Előzmény: [1506] nadorp, 2006-11-14 12:19:34 |
|
|
| [1509] Cckek | 2006-11-14 15:49:20 |
 Kedves Attila. Eddig mintha starpás és mesterkélt lett volna. hmm:) Amúgy ez csak egy feladat, kitűztem mert reméltem, hogy van akinek örömet okoz a megoldása. Ha neked nem, hát akkor ne foglalkozz vele, ez itt nem verseny, és remélem még csak versengés sem.
|
| Előzmény: [1504] jenei.attila, 2006-11-14 11:32:30 |
|
| [1510] jenei.attila | 2006-11-14 16:29:21 |
 Egyáltalán nem akartalak megsérteni, szerintem nem is volt rá okod, hogy megsértődj. A véleményemet pedig hadd mondjam már el, én teljesen jószándékúan kérdeztem, hogy mi a feladatban az érdekesség, trükk. Most, hogy már megvilágítottad a feladat hátterét, valóban érdekesebbnek találom, bár még mindíg kicsit "megcsinált" ízű. Egyébként engedd meg, hogy azzal a feladattal foglalkozzak, amelyik nekem tetszik, a versengéssel kapcsolatban meg nem értem mire gondolsz.
|
| Előzmény: [1509] Cckek, 2006-11-14 15:49:20 |
|
| [1511] Cckek | 2006-11-14 19:03:42 |
 Jó, részemről befejezve felejtsük el:)) Itt van egy megint csak érdekes feladat:)) Hány n-edrendű permutáció inverzióinak a száma k???
|
|
| [1512] nadorp | 2006-11-15 17:03:41 |
 Félek tőle, hogy erre nincs zárt formula. Ha tévedtem, akkor annál jobb. Az az erős sejtésem ( bár ez is kétséges, úgyhogy ne dobáljatok meg kővel), hogy ha a keresett számot I(n,k)-val jelöljük, akkor az
fn(x)=(1+x)(1+x+x2)...(1+x+...xn-1) polinomban xk együtthatója éppen I(n,k)
|
| Előzmény: [1511] Cckek, 2006-11-14 19:03:42 |
|
| [1513] jenei.attila | 2006-11-15 19:27:32 |
 A feladat megtalálható Lovász László Kombinatorikai problémák és feladatok c. könyvében. Itt a megoldást az ún. inverzió vektorok használatával adják meg. Egy n-ed rendű p permutáció inverzió vektora egy n elemű t vektor (tömb), amelynek j-edik eleme azt adja meg, hogy a permutációban hány előző elem kisebb, mint a j-edik elem: tj=|1<=i<j:p(i)>p(j)|, vagyis rögzített j mellet a kisebb indexekkel képezhető inverziók számát. Világos, hogy 0<=tj<=j-1, és a t elemeinek összege éppen a p inverzióinak számát adja. Fordítva is igaz: egy feltételeknek megfelelő t vektor egyértelműen meghatározza a p permutációt (ez is egy érdekes kis feladat). Ezért a k=t1,+t2+...+tn egyenlet feltételnek megfelelő (0<=tj<=j-1) megoldásait kell összeszámolni, vagyis k hányféleképpen írható fel ilyen módon n db. szám összegeként. Ennek az ún. partíciós problémának a megoldását adja a Nadorp által felírt polinom k-ad fokú tagjának együtthatója.
Erre a megoldásra gondoltál?
|
| Előzmény: [1511] Cckek, 2006-11-14 19:03:42 |
|
|
|
|
| [1517] jenei.attila | 2006-11-16 15:50:44 |
 Egyébként (mint azóta utána néztem), D.E. Knuth: A számítógépes programozás művészete c. könyv harmadik kötete (Rendezések és keresések) is részletesen foglalkozik a problémával. Ott egy érdekes rekurziót is megad. A könyvet nagyon ajánlom mindenkinek.
|
| Előzmény: [1516] jenei.attila, 2006-11-16 15:44:31 |
|
| [1518] nadorp | 2006-11-18 10:22:10 |
 Megpróbálom vázolni a gondolatmenetemet. Jelölje az n-edrendű k inverziót tartalmazó permutációk számát I(n,k) és legyen p(n,k) egy ilyen permutáció. Ekkor ha az n+1 elemet a permutáció végére tesszük, akkor egy p(n+1,k) permutációt kapunk. Ha az n+1-et eggyel balra tolva a n-dik helyre tesszük, akkor egy p(n+1,k+1) permutációt kapunk stb. ha az n+1 az első helyen van, akkor egy p(n+1,k+n) permutációt kapunk. Foglaljuk be ezt az alábbi táblázatba, ahol a k-dik oszlopban a p(n,k)-ból kapható permutációk találhatóak.
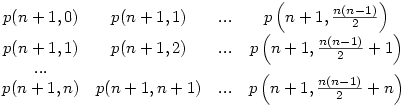
Tekintsük még a következő hasonló táblázatot
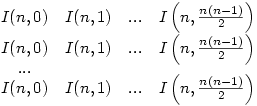
Nyilvánvaló, hogy I(n+1,k) úgy kapható meg, hogy ahol az első táblázatban p(n+1,k) van, összeadjuk a második táblázatban az ezeken a helyeken szerplő I(n,...) értékeket.Tehát
I(n+1,0)=I(n,0)
I(n+1,1)=I(n,0)+I(n,1)
I(n+1,2)=I(n,0)+I(n,1)+I(n,2) stb..
Ezek az összegek éppen balról jobbra haladva a "balról jobbra fel átlókon" levő elemek összege. Ha most fn(x) az I(n,k) sorozat (n fix) generátor függvénye, azaz
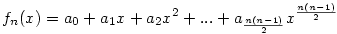 , ahol ak=I(n,k), akkor , ahol ak=I(n,k), akkor
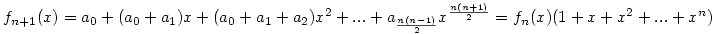
|
| Előzmény: [1516] jenei.attila, 2006-11-16 15:44:31 |
|
| [1519] Cckek | 2006-11-18 11:51:16 |
 Nagyon érdekes okfejtés. Az nyílvánvaló, már csak az inverziók számolási módszeréből is, hogy a t1+t2+...+tn-1=k összeg összes lehetséges képzésének a száma adja meg az n-edrendű k inverzióval rendelkező permutációk számát, hiszen ha a permutáció alsó sorában 1 előtt t1, 1-nél nagyobb, 2 előtt t2, 2-nél nagyobb,.. (n-1) előtt tn-1, (n-1)-nél nagyobb elem van akkor a permutáció inverzióinak a száma t1+t2+...+tn-1. Az is látható, hogy 0 t1 t1 (n-1), 0 (n-1), 0 t2 t2 (n-2),...,0 (n-2),...,0 tn-1 tn-1 1 Tehát, a problémát, kitűnően letárgyáltátok, itt valóban nem beszélhetünk zárt alakról, annyit még hozzátennék, hogy amennyiben Skn-el jelöljük a k inverzióval rendelkező n-edrendű permutációk számát úgy fennáll : 1 Tehát, a problémát, kitűnően letárgyáltátok, itt valóban nem beszélhetünk zárt alakról, annyit még hozzátennék, hogy amennyiben Skn-el jelöljük a k inverzióval rendelkező n-edrendű permutációk számát úgy fennáll :
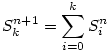
Attila is említett egy rekurziót. Az hogy néz ki?
|
| Előzmény: [1518] nadorp, 2006-11-18 10:22:10 |
|
| [1520] Cckek | 2006-11-18 11:59:12 |
 Még valami. Az vajon eldönthető-e, hogy egy k inverzióval rendelkező n-edrendű permutáció hányféle képpen bontható fel transzpozíciók szorzatára? Én ezzel probálkoztam, persze nem jutottam sehova.:)
|
|
| [1521] Lóczi Lajos | 2006-11-19 17:44:40 |
 Oldjuk meg a valós számok halmazán a
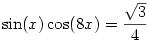
trigonometrikus egyenletet.
|
|
|
|
|
|
|
|
|
| [1529] Lóczi Lajos | 2006-11-22 22:26:15 |
 Csak 4 dolgot nem értek:
1. mi a különbség hi és Hi között
2. mit jelöl a  függvény függvény
3. mit jelöl a kapcsoszárójel
4. mire vonatkozik a limesz, ugyanis a szummában nincs már szabad változó
(Jobban érteném hi jelentését, ha látnám az első pár tagját.)
|
| Előzmény: [1528] S.Ákos, 2006-11-22 20:00:39 |
|
|
| [1531] Sirpi | 2006-11-22 22:53:47 |
 Lehet hogy rosszul gondolom, de én az állítást úgy értelmeztem, hogy azon egészek reciprokösszege, melyekre teljesül, hogy nem osztja őket a nála kisebb relatív prímek száma, végtelen.
|
| Előzmény: [1529] Lóczi Lajos, 2006-11-22 22:26:15 |
|
|
|
|
| [1535] jenei.attila | 2006-11-23 11:24:47 |
 Én sem egészen értem a feladatot, de ha azon számok reciprok összegéről van szó, amelyeknek a náluk kisebb relatív prímek száma nem osztója, akkor a páratlan prímekre ez biztos igaz. Ezek reciprok összege, pedig valóban divergens, és következik belőle, hogy a szóban forgó számok reciprok összege is divergens. A prímekre vonatkozóan a bizonyítás nem túl könnyű, és lehet, hogy az Ákos által megfogalmazott gyengébb állítás bizonyítása könnyebb. Szerintem ez lehet a feladat.
|
| Előzmény: [1534] Lóczi Lajos, 2006-11-23 10:15:36 |
|
| [1536] jenei.attila | 2006-11-23 12:01:16 |
 Sőt. A páratlan számokhoz relatív prímek száma páros, vagyis nem lehet osztója a páratlan számnak. A páratlan számok reciprok összege pedig divergál. Szerintem kérdezzük meg Ákost, pontosam mire gondolt. Ákos! A kérdés adott: légyszíves pontosítsd a feladatot. Köszi.
|
| Előzmény: [1535] jenei.attila, 2006-11-23 11:24:47 |
|
|
|
| [1539] jenei.attila | 2006-11-23 20:55:29 |
 Valóban, ez esetben a hányados tényleg 2, azonban a lényegen mit sem változtat. Egyébként ez az eset is benne van az előző hozzászólásomban, l=0-val. Az ez előtti megjegyzésem szerint, minden páratlan számra igaz, hogy a  (n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz. (n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz.
|
| Előzmény: [1538] S.Ákos, 2006-11-23 20:09:58 |
|
| [1540] Cckek | 2006-11-25 23:02:45 |
 Oldjuk meg az egész számok halmazán a következő egyenletet: 2m-1=xn
|
|
| [1541] Cckek | 2006-11-26 11:52:55 |
 Adjunk páldát olyan an sorozatra, melyre 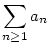 konvergens, de nan határértéke nem 0. konvergens, de nan határértéke nem 0.
|
|
|
|
| [1544] ScarMan | 2006-11-26 13:41:17 |
 Szerintem ebben az esetben a határérték csak 0 lehet.
Ha an-nek végtelen sok pozitív és negatív tagja van, akkor ez nan-re is igaz, de ekkor a két részsorozat közös határértéke csak a 0 lehet.
Ha valamelyik előjelű tagból csak véges sok van, akkor azokat hagyjuk el. Ha most csak negatív tagjaink maradtak, akkor szorozzuk az egészet -1-gyel. Most csak pozitív tagjanik vannak. Itt találunk egy szig. mon. csökkenően 0-hoz tartó részsorozatot, ez legyen aN. Nyilván 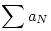 is konvergens, mert pozitív tagokat hagytunk el. Ekkor a Cauchy-féle ekvikonvergencia tétel miatt is konvergens, mert pozitív tagokat hagytunk el. Ekkor a Cauchy-féle ekvikonvergencia tétel miatt 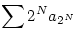 sor is konvergens, ezért az általános tag 0-hoz tart. Ez NaN-nek részsorozata, ami viszont nan-nek részsorozata, tehát nan-nek 0 torlódási pontja. sor is konvergens, ezért az általános tag 0-hoz tart. Ez NaN-nek részsorozata, ami viszont nan-nek részsorozata, tehát nan-nek 0 torlódási pontja.
|
| Előzmény: [1543] Cckek, 2006-11-26 12:12:20 |
|
|
|
|
| [1548] Cckek | 2006-11-26 15:40:18 |
 Most már egyszerű bebizonyítani azt is,hogy ha: 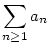 konvergens akkor konvergens akkor
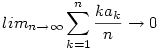 . .
Gondolkozzunk a következő határértéken:

|
|
|
| [1550] Csimby | 2006-11-28 23:01:50 |
 241.feladat
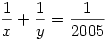
Keressük a pozitív egész megoldásokat. (Lehet, hogy már volt, ez esetben sorry)
|
|
| [1551] Hajba Károly | 2006-11-29 00:49:24 |
 Rendezzük az egyenletet:
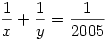
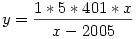
Ahhoz, hogy y egész lehessen, a nevező értékének a számláló valamely részszorzatával kell egyenlőségben lennie. Ez 7 megoldást ad, melyből 3-3 'szimmetrikus'.

|
| Előzmény: [1550] Csimby, 2006-11-28 23:01:50 |
|
|
|
| [1554] lorantfy | 2006-11-30 10:35:07 |
 300. feladat. Egységnyi szakaszt véletlenszerűen 3 részre vágunk szét. Mekkora a valószinüsége, hogy a három részből háromszög szerkeszhető? (TK. példa)
|
|
|
|
|
|
|
| [1559] jenei.attila | 2006-11-30 14:53:57 |
 Látom közben neked is ez jött ki, ez biztató. Egyébként én az x,y síkbeli koordináta rendszer (0,0), (1,0), (1,1), (0,1) egységnégyzetében veszek fel egy pontot (egyenletes eloszlás szerinti valószínűséggel), amelynek x ill. y koordinátája megadja a [0,1] intervallum egy felosztását. Az x, y-x, 1-y (ha x<=y) szakaszokból pontosan akkor szerkeszthető háromszög, ha mindegyik hossza 1/2-nél kissebb. A koordinátarendszerben ábrázolva azt jelenti, hogy a kivélasztott pont az x=1/2, y=1/2, y=x+1/2 egyenesek által határolt háromszögbe esik. Ennek területe 1/8. Amikor x>y, hasonlóan egy 1/8 területű háromszög lesz a megfelelő tartomány. Tehát a keresett valószínűség 1/4.
|
| Előzmény: [1557] Sirpi, 2006-11-30 14:27:02 |
|
| [1560] jenei.attila | 2006-11-30 14:56:23 |
 Közben látom te is megelőztél a feltöltéssel, én is az ábrádhoz hasonló háromdxögre gondoltam. Csak nem vetted figyelembe a másik esetet, amikor x>y. Én kitartok az 1/4 mellett.
|
| Előzmény: [1568] Ali, 2006-11-30 14:53:10 |
|
| [1561] nervus | 2006-11-30 16:56:31 |
 Üdv! Tudnátok segíteni 1 feladatban? Már órák óta gondolkozom rajta, de nem jöttem rá :( Egy üres, 100 szobás szállodában unatkozik a portás:) Elindul, és felkapcsol minden villanyt. Aztán visszafordul, és lekapcsol minden 2. lámpát. Majd újra elindul (3. kör) és minden 3. lámpát átvált (ha le van kapcsolva, felkapcsolja, ha fel, lekapcsolja). Ahanyadik kört teszi meg (vagyis csak 100 lehet), annyiadik szobának a lámpáját változtatja meg. (10 kör, minden 10. lámpa.. stb) Aki tudja, help légyszi:S
|
|
| [1562] nervus | 2006-11-30 17:10:55 |
 Jah, maga a kérdés az az, hogy a végére hány lámpa marad égve? Előre is köszi:)
|
|
| [1563] rizsesz | 2006-11-30 17:53:35 |
 pontosan 10. ugye egy lámpát pontosan annyiszor vált át, ahány osztója van. két érdekes állapot van, a lekapcsolt, illetve a felkapcsolt villany. a felkapcsolthoz páratlan sok, a másikhoz páros sok váltás kell. így azok maradnak égve, amelyeknek páratlan sok osztója van, ezek a négyzetszámok, amelyekből 10 darab van (1, 4, 9...100).
|
|
|
| [1565] nervus | 2006-11-30 18:05:24 |
 Az utolsó kérésem, hogy leírnád ezeket a négyzetszámokat? Hátha érdekli majd a matektanárom, hanyas szobákban maradnak égve a lámpák :) Köszönet és hála
|
|
|
|
| [1569] Tappancsa | 2006-12-01 20:55:18 |
 Ez a feladat a klasszikus példája a rosszul definiált valszám feladatnak. Mit jelent a "véletlenszerű" szétvágás? Néhány lehetőség:
1. Egymástól függetlenül kiválasztunk két pontot - ott vágjuk el.
2. Kiválasztunk véletlenszerűen egy pontot - az lesz az egyik vágás, aztán véletlenszerűen kiválasztjuk az egyik szakaszt és azt is véletlenszerűen ketté vágjuk.
3. Ugyanaz, mint előbb, de mindig a nagyobbik szakaszt osztjuk fel a második lépésben (mert ha a kisebbiket, akkor biztos nem lehet háromszög).
Az első két opció mindenestre logikusan hangzik. A vicc az, hogy különböző választ adnak.
Anikó
|
| Előzmény: [1554] lorantfy, 2006-11-30 10:35:07 |
|
| [1570] Nick | 2006-12-01 21:29:56 |
 Sziasztok!
Most találkoztam a fórummal és egyből végig is olvastam az egészet:)
Már itt is felmerült az a feladat, hogy egy n hosszú 0-1 sorozatban mi a valsz.-e, hogy van legalább k hosszú egyforma sorozat. Az akkori reagálás rá számomra kissé nehézkes volt és szeretném ha vki képletet adna rá (bizonyítás nélkül akár), n és k függyvényében. (előre is köszi a segítséget)
(más): Megkérdezte itt valaki, hogy hogyan határozzák meg a felvételi ponthatárokat, és a válasz rá sztem nem volt elég matematikus:) Úgy hogy szeretném ezt kitűzni feladatként:
Mennyi lesz jövőre (pl) az ELTE mat. szakjára a felvételi ponthatár? Persze ez így önmagában rosszul hangzik, és igen sok lenne benne a paraméter, ezért egy kicsit egyszerűsítsük a problémát. (Lényegében azt az eljárást keressük, hogy hogyan vesznek föl vkit egy egyetemre). Nézzük a következő feladatot: Egy házasságközvetítő irodában 100 férfi és 100 nő van nyílvántartva, minden férfi (és minden nő) rangsorolja az összes nőt (férfit), hogy melyiket választaná legszivesebben, másodiknak stb. A mi feladatunk, hogy olyan párosítást találjunk ami megfelelő mindkét fél számára. Azaz legyen az A1 által előálított rangsorban B1 a k. helyen. Minden k-nál előrébb álló Bi párjának a rangsorban(Bi által meghatározott) elfoglat helye legyen kisebb mint A1-é. ( De nehéz ezt leírni:); ha elírtam volna vagy nehezen értelmezhető akkor: azt szerettem volna leírni, hogy ha pl nekem választanak ki egy nőt, akkor az összes általam előrébb rangsorolt nőnek a férje az ő ranglistáján előbrébb legyen mint én; azaz ne legyen két olyan ember akik jobban akarják egymást mint a nekik kiosztottat).
Találjunk olyan módszert, eljárást ami a kívánt feltételt teljesíti. És ha ez már megvan, akkor jöhet a ponthatár:)
|
|
| [1571] Róbert Gida | 2006-12-01 21:42:25 |
 Stabil házasság problémája ez. Valóban, az egyetemi felvételinél is ezt az algoritmust futtatják, tudtommal az egyetemek felől és nem a jelentkezők szempontjából ráadásul.
|
| Előzmény: [1570] Nick, 2006-12-01 21:29:56 |
|
| [1572] Nick | 2006-12-02 13:04:55 |
 Hát persze hogy az:) És persze gyorsan meg is található a neten, de sztem van annyira érdekes a megoldás, hogy egyedül jöjjünk rá. (nekem nem is ment addig, míg meg nem mondták, hogy a megoldást az életből lopták:))
|
|
| [1573] Lóczi Lajos | 2006-12-03 20:49:25 |
 Adjuk meg azokat a 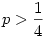 számokat, amelyek esetén a számokat, amelyek esetén a
p, p2+p, (p2+p)2+p, ((p2+p)2+p)2+p, (((p2+p)2+p)2+p)2+p, ...
sorozat korlátos.
|
|
| [1574] epsilon | 2006-12-04 07:17:56 |
 Kedves Lajos! A sorozatot rekurzióval így írhatjuk: a(1)=p és a(n+1)= a(n)×a(n)+1. Mivel p>1/4 ezért a(n+1)>a(n)×a(n)+1/4>=a(n) teljes négyzettel látható. Tehát a sorozat monoton növekvő, így csak a felső korlátja érdekel. Tegyük fel, hogy van felső korlátja, megkeressük a legjobbat, a supremumot. Mivel a sorozat monoton növekvő és korlátos, ezért van limesze, legyen a=lim a(n). A rekurzióban a határértékre térve, megoldva a 2. fokú egyenletet, annak a pozitív gyöke felel meg, ez a=(1+sqrt(1-4p))/2 vagis éppen ez lesz a legjobb felső korlát (indukcióval igazolható, a rekurziót használva), és ez a felső korlát MINDEN p>1/4 esetén létezik! Remélem, ilyen hajnalban nem tévedtem! ;-) Üdv: epsilon
|
| Előzmény: [1573] Lóczi Lajos, 2006-12-03 20:49:25 |
|
|
| [1576] jenei.attila | 2006-12-04 11:55:38 |
 Lehet, hogy butaságot kérdezek, de epsilon levezetése szerint p>1/4 esetén a sorozat tényleg monoton növő, és ekkor ha van felső korlátja, akkor konvergens is. Ha pedig konvergens, akkor csak az lehetne a határértéke, amit epsilon megadott. Na de az nem valós, ebből szerintem az következik, hogy nincs határértéke, de akkor nem is korlátos. Mit szóltok hozzá?
|
| Előzmény: [1573] Lóczi Lajos, 2006-12-03 20:49:25 |
|
| [1577] Sirpi | 2006-12-04 12:36:29 |
 Ebben a hozzászólásban én némi zavart látok, pl. nem tudom miért nem a p2+p=p egyenletet vizsgáljuk, aminek triviálisan csak a p=0 megoldása (mintha a p p2+1 rekurzió is belekeveredett volna a dologba). p2+1 rekurzió is belekeveredett volna a dologba).
Viszont azt, hogy a sorozat sosem korlátos, a következőképp is belátható:
Legyen x=p-1/4>0, vagyis az első tag ennyivel van 1/4 felett. Ekkor a második tag eltérése 1/4-től:
p2+p-1/4=(x+1/4)2+(x+1/4)-1/4=x2+3/2.x+1/16>3/2.x
Vagyis a következő tag 1/4-től való eltérése legalább másfélszer akkora lesz, mint az elsőnek, így a sorozat minden p>1/4 esetén exponenciálisan nőni fog.
|
| Előzmény: [1574] epsilon, 2006-12-04 07:17:56 |
|
| [1578] jenei.attila | 2006-12-04 12:53:18 |
 Szerintem epsilon csak elírta a rekurziót, mert utána már jól használja. Helyesen: a1=p,an=an-12+p A Te egyenleted, viszont nem jó, mert nem az előző tag négyzetéhez adja az előző tagot, hanem az előző tag négyzetéhez mindig p-t. Így a levezetésed sem jó, csak az első két tagra.
|
| Előzmény: [1577] Sirpi, 2006-12-04 12:36:29 |
|
| [1579] epsilon | 2006-12-04 13:24:56 |
 Bocs, valóban elírtam :-( túl korán reggel volt, és éppen egy szünetben olvastam: a helyes egyenlet úgy ahogyan javítoták, így a limeszre térés után a=a×a+p ahonnann a beszámítható "a" amit írtam, valóban komplex szám (itt sem figyeltem a p>1/4-et (illetve pont fordítva láttam :-( de tudjuk azt, hogy a sorozat monoton növekvő, és ha felülről korlátos lenne, akkor a legjobb felső korlát, a supremum, éppen ez az a=lim a(n) kellene legyen, vagyis úgy tűnik (?), hogy a p>1/4 feltétellel ellentmondásba kerülünk (?) vagyis nem létezne p>1/4 amire korlátos lenne(?)
|
|
| [1580] epsilon | 2006-12-04 13:46:29 |
 Végül is elgondolkozva, a leírtakból erre következtetek: ha p>1/4 akkor a sorozat monoton növekvő és korlátlan, az az divergens. Erre jutok akkor is, ha a(n+1)=f(a(n)) típusú rekurzióként kezelem, ahol f(x)=x*x+p és bevezetve g(x)=f(x)-x jelölést, g(x)=1/4*(2x-1)*(2x-1)+p-1/4>0 ami azt jelenti, hogy a fentiekben értelmezett sorozat monoton növekvő és korlátlan!
|
|
| [1581] Lóczi Lajos | 2006-12-04 14:01:58 |
 Köszönöm a szép hozzászólásokat, igen, tehát tetszőleges p>1/4 esetén a szóban forgó an sorozat + -be divergál. -be divergál.
Folytatás. Adjuk meg azokat a p<-2 értékeket, melyekre az illető sorozatunk korlátos.
|
|
|
| [1583] epsilon | 2006-12-04 15:26:56 |
 Nézzük csak a p<-2 esetet. Hátha megint nem írok el valamit! Szóval használom az előző g(x)=f(x)-x=x*x-x+p függvényt, és igazolom, hogy p<-2 mellett g(x)>0 így amennyiben a(1)<-2 márpedig ez igaz (mert p-vel egyenlő), úgy a sorozat megint monoton növekvő lesz. Az x*x-x+p=0 zérushelyei a következők: x(1)=(-1-sqrt(1-4p))/2 illetve x(1)=(-1+sqrt(1-4p))/2. Könnyen igazolható, hogy a p<-2 miatt x(1)<-2, ezért amikor a(1)=p<x(1)<-2 ekkor g(x)>0 (a trinom a gyökökön kivűl a főegyütthatók előjelével egyező előjelű), ami azt jelenti, hogy a a(n+1)=f(a(n))rekurzióval értelmezett sorozat monoton növekvő. Ha korlátos lenne, akkor konvergens is lenne, és a limesze éppen a=x(1)=(-1-sqrt(1-4p))/2 lenne, vagyis ez lenne a felső korlát. Közben most látom, hogy Cckek máris írt, de még nem mérlegeltem, ezt elengedem, aztán azt is mérlegelem.
|
|
| [1584] epsilon | 2006-12-04 15:36:55 |
 Gratulálok Cchek, nagyon elegáns bizonyítás a monotonításra,...hmmm...ezek szerint a korláttal megint elnéztem valamit...:-(
|
|
|
| [1586] Lóczi Lajos | 2006-12-04 15:44:49 |
 Tényleg nagyon tömör :)
Akkor most már "csak" az a kérdés, hogy hogyan viselkedik a sorozat az eddig kimaradt ![p\in \left[-2,\frac{1}{4}\right]](keplet.cgi?k=9475F8E6DDD4364B) paraméterértékek esetén. Adjunk meg minél bővebb részhalmazokat a paraméterértékek esetén. Adjunk meg minél bővebb részhalmazokat a ![\left[-2,\frac{1}{4}\right]](keplet.cgi?k=BF8701E4C127A47C) intervallumból, amely p számok mellett an (a 0-ból indítva) konvergens. intervallumból, amely p számok mellett an (a 0-ból indítva) konvergens.
|
| Előzmény: [1582] Cckek, 2006-12-04 15:17:55 |
|
|
|
|
| [1590] Cckek | 2006-12-04 17:25:29 |
 Esetleg vizsgálható a
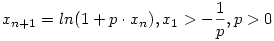
sorozat is.
|
|
| [1592] Cckek | 2006-12-04 20:56:58 |
 hogyan igazoljuk hogy kontinuum sok kontinuum számosságú halmaz egyesítése kontinuum számosságú?
|
|
| [1593] Csimby | 2006-12-04 21:36:10 |
 Ennek c2 eleme van, hiszen c féle képpen választhatjuk meg hogy melyik halmazból veszünk elemet, és azon belül is még c elem közül választhatunk. És c2=(2A)2=22A=2A=c , ahol A jelöli alef 0-t, a természetes számok számosságát és c a kontinuum számosságot.
|
| Előzmény: [1592] Cckek, 2006-12-04 20:56:58 |
|
| [1594] Cckek | 2006-12-04 22:00:40 |
 Ok nagyon szép. Egy direkt bizonyitást a kardinális számokkal végezhető műveletek nélkül? Tehát nem használhatjuk fel hogy k szor alef nulla az szintán alef nulla stb...
|
| Előzmény: [1593] Csimby, 2006-12-04 21:36:10 |
|
| [1595] jenei.attila | 2006-12-05 13:13:37 |
 Pl. "megindexeljük" az unió elemeit a [0,1]x[0,1]-beli valós számpárokkal. A pár első eleme jelenti, hogy melyik halmazból való a kiválasztott elem, a második, hogy azon belül melyik elemről van szó. A halmazok, illetve egy halmaz elemei nyilván indexelhetők [0,1]-beli valós számokkal. A [0,1]x[0,1]-beli valós számpárok halmaza pedig nyilván kontinuum számosságú, ez könnyen látható pl. a pár két számának tizedestört alakban felírt számjegyeinek összefésülésével.
|
| Előzmény: [1594] Cckek, 2006-12-04 22:00:40 |
|
| [1596] HoA | 2006-12-08 18:33:19 |
 Odáig igaz, hogy a nevező a számláló valamelyik részszorzata. Csak arra nem gondoltál, hogy x nem feltétlenül törzsszám - mint ahogy megoldásaidban sem az - legyen x = u * v, ezért a részszorzat olyan is lehet, hogy az 1*5*401 valamilyen s részszorzata u-val szorozva.
s*u=u*v-2005
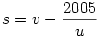
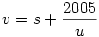
Egészekről lévén szó u is az 1*5*401 valamilyen részszorzata . Végignézve a lehetőségeket, két esetben kapunk a már ismertektől kükönböző megoldást.
s=5;u=5;v=406;x=2030;y=401*406=162806
és
s=401;u=401;v=406;x=162806;y=2030
Tehát ( 2030 ; 162806) és ( 162806; 2030 ) is két "szimmetrikus" értékpár.
|
| Előzmény: [1551] Hajba Károly, 2006-11-29 00:49:24 |
|
|
| [1598] jenei.attila | 2006-12-08 22:21:23 |
 Ez mintha most lett volna Arany Dániel versenyfeladat. Az eredeti egyenlet ekvivalens a következővel:
(x+y)2005=xy
, ez pedig ekvivalens a
(x-2005)(y-2005)=20052
. De 20052=524012, vagyis 9 osztója van, ezért az eredeti egyenletnek 9 megoldása van, Neked ebből csak 7 jött ki. Nem számoltam ki, ezért nem tudom melyik 2 hiányzik.
|
| Előzmény: [1597] Hajba Károly, 2006-12-08 20:20:03 |
|
|
| [1600] Cckek | 2006-12-09 08:00:43 |
 Ha p,q N* számítsuk ki a következő összeget: N* számítsuk ki a következő összeget:
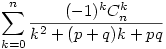
|
|
| [1601] Mhari | 2006-12-10 10:31:21 |
 Sziasztok!
Mi a valószínűsége annak, hogy úgy tudunk megfésülni egy plüssmackót, hogy ne legyen forgója? .
Állítólag létezik egzakt válasz a kérdésre, szóval nem átverés... Megj: Egy Tusnády Gábor nevű matematikust említettek, aki foglalkozik ilyesmivel. Gőzöm sincs, hogy merre induljak el.
Üdv: Mhari
|
|
|
| [1603] AzO | 2006-12-10 18:07:15 |
 Nalunk sundisznoval volt felteve a kerdes topologia gyakorlaton, es az a feladat ekvivalens volt azzal, hogy fujhat-e mindenhol a szel a foldgombon (a szel vektorszeru, es folytonos :) ). Erre a valasz az, hogy mindig van legalabb 1 pont, ahol nem fuj a szel. Meg hasonlo az a feladat is, hogy megkavarod a levest, es lesz olyan "pont", ami a helyen marad. Persze konnyen lehet, hogy felreertettem a feladatot :)
|
| Előzmény: [1601] Mhari, 2006-12-10 10:31:21 |
|
|
| [1605] Lóczi Lajos | 2006-12-10 21:56:17 |
 Angolul ezek a "hairy ball theorem"-ek. A válasz attól függ, hogy a mackó Euler-karakterisztikája mennyi.
Ha pl. 2, azaz folytonos deformációval átdeformálható egy gömbbe (pl. "felfújod"), akkor a tetszőleges, a felületén értelmezett folytonos vektormezőnek létezik zérushelye, azaz lesz a szőrén forgó.
Ha viszont a karakterisztika 0, tehát a maci átdeformálható egy tóruszba, akkor lehet úgy fésülni, hogy ne legyen forgója: egy szőrös úszógumit meg tudsz fésülni így.
|
| Előzmény: [1601] Mhari, 2006-12-10 10:31:21 |
|
|
|
|
| [1609] Mhari | 2006-12-11 23:25:55 |
 Köszönöm a segítséget, különösen Lóczi Lajosnak. Életembe se jutott volna eszembe a "szőrös labda tétel" esete. De lehet, hogy még Euler sem ebben a témában. Azt hittem valami differenciálgeometriai esettel állok szemben. A link jó, ott a megoldás. Még 1x köszönöm a gyors választ!
|
| Előzmény: [1605] Lóczi Lajos, 2006-12-10 21:56:17 |
|
| [1610] Mhari | 2006-12-11 23:32:17 |
 Bocs, a link lemaradt: http://www.math.hmc.edu/funfacts/ffiles/20005.7.shtml
|
|
| [1611] Cckek | 2006-12-12 18:29:35 |
 Határozzuk meg az elipszis racionális kordinátájú pontjait:)
|
|
| [1612] psbalint | 2006-12-13 20:16:58 |
 http://www.asztralfeny.hu/magus/magus.php
egy kis izgalmas sziget a gyilkos feladatok végtelen óceánján... ;)
|
|
|
|
| [1615] Csimby | 2006-12-14 21:02:24 |
 301. feladat Egy 3×3-as négyzet 1×1-es kisnégyzetei közül hányféleképpen színezhetünk ki 4-et úgy, hogy a négyzet szimetriával egymásba vihető színezéseket nem tekintjük különbözőnek.
|
|
| [1616] Hajba Károly | 2006-12-14 22:25:52 |
 Ha egy színnel színezek, akkor, ha nem néztem el valamit, 20. S ebből következtetve 2 szín esetén kevesebb, mint 280, a szimmetrikus alakzatokban fellépő ismétlődések miatt. 4 szín esetén kevesebb, mint 480.
|
| Előzmény: [1615] Csimby, 2006-12-14 21:02:24 |
|
|
|
| [1619] HoA | 2006-12-15 11:23:18 |
 Szerintem az ilyen, még fejben/papíron leszámolható eredményre vezető feladatokat úgy célszerű megoldani, hogy a lehetséges eseteket egy olyan döntési fa mentén derítjük fel, ahol a szimmetrikus esetek azonos ágra kerülnek. Esetünkben például: Van-e színezett saroknégyzet? Színezett-e a középső?
Ha valakinek 22-nál több vagy kevesebb jött ki, itt egy kis ellenőrzési lehetőség. Vagy javítsatok, ha én szúrtam el valamit :-)
|
 |
| Előzmény: [1617] Csimby, 2006-12-15 01:12:24 |
|
|
|
| [1622] HoA | 2006-12-15 11:45:50 |
 Arra azért kíváncsi lennék, a hozzászólók hány százaláka leplezi le az ezoterikus parapszichológiai telepátiát. Mert az ilyen hozzászólást természetesen nem teszi fel a lapra. A "Minden jog fenntartva" témában is lennének aggályaim, ezt már máshol is láttam, például itt:
http://brutalvideos.freeweb.hu/Flash/psychic.htm
|
| Előzmény: [1614] Hajba Károly, 2006-12-14 08:04:24 |
|
|
|
|
|
| [1627] Csimby | 2006-12-16 02:54:25 |
 302.feladat Adott a következő négy szám: 1,3,4,6. A négy alapművelet és a zárójelezés segítségével, mindegyik számjegyet egyszer felhasználva állítsuk elő a 24-et. (aki ismeri az NE lője le a megoldást)
|
|
|
|



 2-től igaz csak...
2-től igaz csak... 






 /q) nem más, mint
/q) nem más, mint  0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem.
0 és f(0):=0, melyeket szokás "lapos" ("flat") függvényeknek is nevezni. Egyszerűen látható, hogy ennek 0-körüli Taylor-sora a konstans 0 függvény, ami nyilván nem állítja elő f-et semmilyen origó körüli intervallumon sem.  valós szám esetén számítsuk ki a
valós szám esetén számítsuk ki a 
 a tört <1, így a megoldások száma lefeleződik...
a tört <1, így a megoldások száma lefeleződik... 
 függvény
függvény 

 =0
=0 
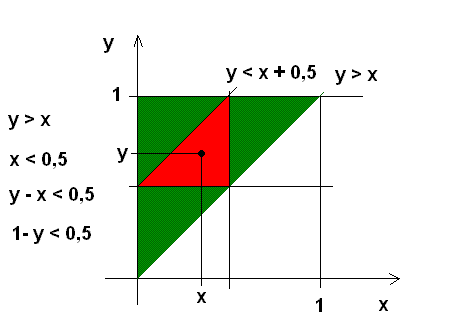

 p2+1 rekurzió is belekeveredett volna a dologba).
p2+1 rekurzió is belekeveredett volna a dologba).  -be divergál.
-be divergál. 
 N* számítsuk ki a következő összeget:
N* számítsuk ki a következő összeget: 



