|
|
| [1078] Sirpi | 2005-10-18 10:29:55 |
 Na, ez a feladat nagyon tetszett, nem hallottam még korábban, csak mindenféle elcsépelt egyféle bábos felpakolásokat.
8x8-asra k=5, 10x10-re k=7 (tovább még nem volt időm vizsgálódni), mindkettőre van konstrukcióm, és könnyű látni, hogy többet nem lehet felrakni. Utóbbinak leírom a bizonyítását, ábrát egyelőre nem teszek fel.
Szóval ha egy nxn-es sakktáblára fel lehet tenni k db bástyát és futót egyszerre, akkor teljesülnie kell az (n-k)2 k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2 k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2 k, ahonnan viszont adódik, hogy k, ahonnan viszont adódik, hogy 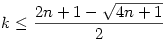 , ez pedig n=8-ra , ez pedig n=8-ra 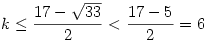 , tehát ekkor k<6, vagyis k , tehát ekkor k<6, vagyis k 5. Hasonlóan adódik n=10-re, hogy k 5. Hasonlóan adódik n=10-re, hogy k 7. 7.
Ez utóbbi nehezebb különben, mert míg 8-ra 5 db futónak kell elférnie egy 3x3-as területen, addig 10-re ugyanígy egy 3x3-as részre 7 futót kell bepréselni.
|
| Előzmény: [1073] rizsesz, 2005-10-17 00:28:27 |
|
|
|
|
| [1073] rizsesz | 2005-10-17 00:28:27 |
 201. feladat.
Adott egy 8*8-as sakktábla, és a k pozitív egész. Mekkora k maximális értéke, ha létezik hozzá olyan elrendezése k darab futónak és k darab bástyának egyazon sakktáblán, hogy egyik bábu sem üti a másikat?
|
|
| [1072] Lóczi Lajos | 2005-10-16 23:36:48 |
 200. feladat. Adjuk meg azt a p valós számot, amelyre az
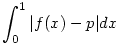
integrál értéke minimális, ha
f(x)=1-e-x2.
|
|
| [1071] jonas | 2005-09-14 21:38:33 |
 Ezt véletlenül ismerem, mert egyszer javítottam a megoldásait.
a: Nem.
b: Csak a c3, f3, c6, f6 mezők valamelyikét hagyhatjuk el.
Három színnel átlósan kell színezni a sakktáblát (vagy lehet nem átlósan, hanem soronként is, úgy, hogy minden dominó alatt hárommal osztható összeg álljon).
|
| Előzmény: [1065] Csimby, 2005-09-14 00:03:02 |
|
|
|
|
| [1067] nadorp | 2005-09-14 16:45:54 |
 Lehet, hogy félreérthető a megfogalmazás:
a ... tört részt jelent.
|
|
| [1066] nadorp | 2005-09-14 16:19:56 |
 Szia Rizsesz !
A b) verziót szerintem a következőképpen lehetne értelmezni:
Legyenek n és k pozitív egészek és legyen
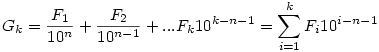
Bizonyítsuk be, hogy létezik egy olyan n pozitív egész és egy k1<k2<... indexsorozat, hogy a
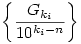 sorozat konvergens és határértéke egy prím reciproka. sorozat konvergens és határértéke egy prím reciproka.
|
| Előzmény: [1060] rizsesz, 2005-09-11 16:52:33 |
|
| [1065] Csimby | 2005-09-14 00:03:02 |
 199.feladat A 8×8-as sakktábla egyik sarkából kivágunk egy 1×1-es négyzetet.
a. Lefedhető-e a megmaradt sakktábla 3×1-es téglalapokkal?
b. Ha a teljes sakktáblából akárhonnan kivághatunk egy 1×1-es négyzetet, honnan tegyük ezt meg ahhoz, hogy a megmaradt tábla lefedhető legyen 3×1-es téglalapokkal?
|
|
| [1064] Sirpi | 2005-09-13 15:44:55 |
 198. feladat: Mely pozitív egészek egyeznek meg 4 legkisebb pozitív osztójuk négyzetösszegével? Mi a helyzet 4 helyett 3-ra?
|
|
|
| [1062] jonas | 2005-09-12 21:42:51 |
 Szerintem igen.
Ugyanis a polinom deriváltja is polinom, tehát folytonos, tehát lokálisan korlátos változású, tehát felírható két monoton növő függvény különbségeként. Ezeket tagonként határozatlanul integráljuk (a konstansra is vigyázva), és megkapjuk a polinomot két konvex függvény különbségeként.
|
| Előzmény: [1061] Káli gúla, 2005-09-12 20:54:13 |
|
|
| [1060] rizsesz | 2005-09-11 16:52:33 |
 Kedves Lorantfy! A tesztversenyen volt az a Fibonacci számos feladat. annak van egy b., verziója, amibe még régebben ütköztem bele, de valahogy nem volt se füle, se farka :) Az a feladat, hogyha a Fibonacci sorozat elemeit egy-egy tizedeshellyel eltolva (akár balról jobbra, akár jobbról balra haladva) egymás alá írjuk és összeadjuk, akkor a sok szám összege végül ismétlődő szakaszokból fog állni, tehát olyan lesz, mint a végtelen szakaszos tizedestörtek. Sőt, nem csak olyan, hanem az is! Ha megfelelő helyre tesszük a tizedesvesszőt, akkor a két összeg éppen 1/A, illetve 1/B értékű lesz, ahol A és B prímszámok. Mennyi A értéke, ha jobbra tolva írjuk egymás alá az elemeket és mennyi B értéke, ha balra? A balra irány így néz ki valahogy:
00001
0001
002
03
5
|
| Előzmény: [1050] lorantfy, 2005-09-02 16:35:32 |
|
| [1059] Lóczi Lajos | 2005-09-10 23:51:47 |
 197. feladat. Legyenek f és g az egész számegyenesen értelmezett konvex függvények, amelyek semelyik intervallumon sem esnek egybe. Legfeljebb hány megoldása lehet az f(x)=g(x) egyenletnek?
|
|
| [1058] qer | 2005-09-10 14:15:30 |
 Ez adta az ötletet: Bármely poliéderbe beirt gömb sugara: 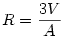 . Picit átrendezve: . Picit átrendezve: 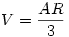 . .
Van egy ehhez hasonló tétel a síkban is: Egy kör köré írt sokszög területe feleakkora, mint a sokszög kerületének és a kör sugarának a szorzata. Azaz: 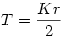 . .
Az analóg n dimenziós tételek igazak-e?
|
| Előzmény: [1010] xviktor, 2005-08-13 01:19:00 |
|
| [1057] Lóczi Lajos | 2005-09-05 22:24:07 |
 Az ilyen típusú feladatoknál jól használható az alábbi azonosság (a megfelelő értelmezési tartományok figyelembe vételével):
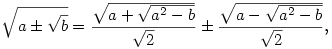
tehát ha a2-b négyzetszám, a dupla gyök mindig kiküszöbölhető.
|
| Előzmény: [1056] Csimby, 2005-09-05 20:53:00 |
|
| [1056] Csimby | 2005-09-05 20:53:00 |
 196. feladat: Állítsuk elő két négyzetgyök összegeként:
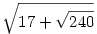
|
|
|





 k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2
k egyenlőtlenségnek. Ez úgy jön ki, hogy a k db bástya mind külön sort és oszlopot kell, hogy elfoglaljon, így a futóknak már csak egy (nem feltétlen egybefüggő) (n-k)x(n-k)-s részrácson marad hely. Itt el kell férnie mind a k futónak, innen jön, hogy (n-k)2 5. Hasonlóan adódik n=10-re, hogy k
5. Hasonlóan adódik n=10-re, hogy k

