| [118] Gyuri | 2003-12-01 04:26:07 |
 Kedves Laszlo!
Bizonyara az ejszakazasnak tudhato be a tevesztese.
A 24.c feladathoz pont az 1. pelda szolgaltat egy megoldast:
A=(1011+1).11-2.102=82644628100.
Hasonloan megoldas meg: (1011+1).11-2.i2 a kovetkezokre: i=4,5,6,7,8,9
A teljes megoldast ilyen koran mar nincs erom leirni...
Udv: Gyuri
|
| Előzmény: [117] lorantfy, 2003-12-01 00:24:24 |
|
| [117] lorantfy | 2003-12-01 00:24:24 |
 Kedves Nádor P.!
Jó példát adtál. Remélem jó lesz a megoldás is!
Megoldás a 24.c feladatra: Eredeti szövege: Keressünk olyan A pozitív egész számot, melyre igaz, hogy önmaga után leírva még egyszer (pld A=12264 esetén 1226412264) a kapott szám négyzetszám.
Az A-ból képezett „duplázott” szám: AA=k2. Legyen A „n” jegyű szám a 10-es számrendszerben, ekkor
AA=10nA+A=(10n+1)A=k2
A (10n+1)A minden prímtényezője páros (második) hatványon van és (10n+1) A. A.
Ebből az következik, hogy 10n+1-nek tartalmaznia kell legalább egy prímtényezőt második hatványon: p12, a többi páratlan (1) kitevőjű prímtényezőt pedig az A szám is tartalmazza, igy lesz a szorzat négyzetszám. Gondolnunk kell arra is, hogy A szám n jegyű.
Gyakorlatilag: 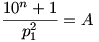 vagy 10n+1=p12A vagy 10n+1=p12A
Nézzük mi lehet ez a p1 prímtényező: 2 és 5 nyilván nem lehet, 3 és 9 nem lehet, mert a számjegyek összege 2.
Lehet 7 és 11. Többet nem is keresünk, ugyanis már ezek is túl nagyok.
Hiszen 10n+1-et 49-el vagy 121-el osztva, az A szám csak (n-1) illetve (n-2) jegyű lesz. Ami azt jelenti, hogy egy vagy két 0-t kéne elé írni, hogy „duplázáskor” a négyzetszám létrejöjjön. Ezt a feladat szövege nem engedi meg.
Így NINCS ilyen A szám!
Érthetőbbé válik a dolog, ha megnézünk egy-két példát, amikor a 0 számjegy segítségével teljesül a feltétel.
1.példa:
1011+1=112 23 4093 8779  A=23 4093 8779 A=23 4093 8779
Szorzatuk:
112 232 40932 87792
négyzetszám. A=826446281 - 9 jegyű szám, igy a szorzat: 82644628100826446281 – négyzetszám.
2.példa:
1021+1=72 11 13 127 2689 459691 909091
A=11 13 127 2689 459691 909091
Szorzatuk:
72 112 132 1272 26892 4596912 9090912
A=20408163265306122449 – 20 jegyű szám, kell elé egy 0-számjegy:
A négyzetszám: 20408163265306122449020408163265306122449
|
| Előzmény: [108] nadorp, 2003-11-28 12:24:24 |
|
| [116] Gyuri | 2003-12-01 00:12:04 |
 Kedves Zoli!
A 25. feladat megoldasa:
ha valamelyik valtozo 0, akkor a tobbi is az. tehat ha valamelyik nem 0, akkor a tobbi sem lehet az. ekkor nyilvan mindegyik pozitiv kell legyen. az egyenletek osszeszorzasabol:
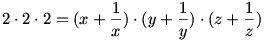
de ez csak x=y=z=1 eseten lehet, hisz a>0 eseten 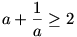 es egyenloseg csak a=1 eseten all fenn. es egyenloseg csak a=1 eseten all fenn.
igy pontosan ket megoldas van.
udv: Gyuri
|
| Előzmény: [111] SchZol, 2003-11-29 21:44:23 |
|
| [115] Hajba Károly | 2003-11-30 01:41:05 |
 Kedves Attila!
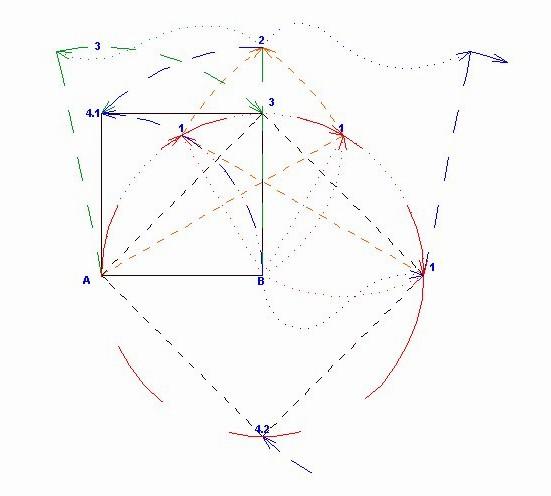
Abban igazad van, hogy mind 20. mind a 21. feladat megoldása a 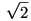 szerkesztése, de a két feladat végeredménye más. Nevezhetjük édestestvéreknek is. Az alábbi ábra mutatja a különbséget és egyben a szerkesztés egyszerűségét is. Nem kell invertálni sem. szerkesztése, de a két feladat végeredménye más. Nevezhetjük édestestvéreknek is. Az alábbi ábra mutatja a különbséget és egyben a szerkesztés egyszerűségét is. Nem kell invertálni sem.
HK
|
 |
| Előzmény: [93] jenei.attila, 2003-11-19 13:00:17 |
|
| [114] SchZol | 2003-11-29 22:07:26 |
 28.feladat: (A verseny 4. feladata)
Az ABCD húrnégyszögben AB=AD és az A csúcsnál lévő belső szög  . Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor . Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor
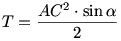
|
|
| [113] SchZol | 2003-11-29 21:55:34 |
 27.feladat: (A verseny 3. feladata)
Az egész együtthatós ax2+bx+c=0 másodfokú egyenletnek két különböző gyöke van a (0;1) nyílt intervallumban. Bizonyítsa be, hogy akkor |a| 5 5
|
|
| [112] SchZol | 2003-11-29 21:46:42 |
 26.feladat (A verseny 2. feladata)
Legfeljebb hány részre oszthatja fel a síkot, a sík egy rögzített pontján áthaladó k darab kör és n darab egyenes, ha k és n pozitív egész szám? Határozza meg a részek maximális számát megadó R(k;n) függvényt!
|
|
| [111] SchZol | 2003-11-29 21:44:23 |
 November 28-án és 29-én került megrendezésre Zalaegerszegen az Izsák Imre Gyula komplex verseny. Íme a matematika példák a versenyről:
25.feladat: (A verseny 1. feladata)
Oldja meg az alábbi egyenletrendszert a valós számhármasok halmazán:
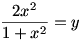
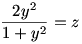
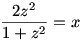
|
|
| [110] lorantfy | 2003-11-29 00:33:28 |
 Kedves Nádor P. és Károly!
Köszönet a megoldásokért! Természetesen A=0, C=0 nem megengedett, mint az az ilyen feladatoknál lenni szokott. Gyakorlatilag megvan a megoldás - persze nem ártana ha valaki szépen összefoglalná. Külön köszönet a 24.c-ért. Én úgy gondoltam a további általánosítást, hogy a "tengelyesen szimmetrikus" számok 7-tel való oszthatóságát kellene vizsgálni, csak még nem volt időm rá.
|
| Előzmény: [108] nadorp, 2003-11-28 12:24:24 |
|
| [109] Hajba Károly | 2003-11-28 13:14:36 |
 Kedves László!
A 24/a feladattal foglalkoztam egy kicsit, s mivel találtam rá példát, így a válasz: lehetséges (pl.: 168 - 861). Ha ragaszkodunk a háromjegyű számhoz, akkor |A-C|=7, tehát a számokpárok 1 és 8-cal ill. 2 és 9-cel kezdődhetnek.
(1) ABC -> 100*A+10*B+C=7*N
(2) CBA -> 100*C+10*B-C=7*M
(2)-(1) 99*(A-C)=7*(M-N)
Mivel 99 nem osztható 7-tel, továbbá M-N oszthatósága jelen esetben közömbös, így A-C mindenképpen osztható 7-tel. Ebből az is következik, hogy M-N osztható 99-cel.
Más a helyzet a 24/b feladattal. Ha a fenti levezetést minden n-re elvégezzük, találunk 7-tel osztható első számot pl.: 9009. Ekkor egyéb vizsgálatok is szükségesek, de most nincs időm rá.
HK
Ui.: A CBA egyes kis- és középboltok egyfajta országos tömörülése, felénk is van(/volt?).
|
| Előzmény: [107] lorantfy, 2003-11-28 00:45:42 |
|
| [108] nadorp | 2003-11-28 12:24:24 |
 Kedves László !
Gondolom, a 24.b feladatban a kérdést úgy értetted, hogy bármely n-re léteznek-e megfelelő A,B,C számjegyek. Én arra jutottam, hogy ha megengeded az A=0 vagy C=0 eseteket, akkor csak n=6k+4 esetén nincs megoldás, ha nem, akkor n=6k és n=6k+4 esetén nincsenek megfelelő számok. A megoldás leírásával még várnék. Viszont csatlakoznék egy hasonló feladattal:
24.c feladat: Keressünk olyan A pozitív egész számot, melyre igaz, hogy önmaga után leírva még egyszer (pld A=12264 esetén 1226412264) a kapott szám négyzetszám.
|
| Előzmény: [107] lorantfy, 2003-11-28 00:45:42 |
|
| [107] lorantfy | 2003-11-28 00:45:42 |
 24.a feladat: Legyenek ABC és CBA tizes számrendszerbeli számok, ahol A,B,C különböző számjegyeket jelölnek. Lehetséges-e, hogy mindkét szám osztható 7-tel?
24.b feladat: Legyenek ABB...BBC és CBB...BBA tizes számrendszerbeli számok, ahol "A" és "C" számjegyek között n darab "B" számjegy áll és A,B,C különböző számjegyeket jelölnek. Lehetséges-e, hogy bármely n-re mindkét szám osztható 7-tel?
Megjegyzés1: Sajnos felülvonást nem tudok húzni, ha valaki tud, kérem írja be a TeX témába!
Megjegyzés2: Mifelénk az ABC áruházakból CBA-k lesznek. Erről jutott eszembe ez a feladat.:-)
|
|
|
| [105] oroszgy | 2003-11-25 15:09:39 |
 Kedves Jenei Attila!
gyök2(TeX még folyamatban...) hosszúságú szakaszt lehet kapni ha egy 1 egység oldalú négyzetnek behúzzuk az átlóját.
|
|
| [104] lorantfy | 2003-11-24 12:00:57 |
 Kedves Károly!
Köszönet a kimerítő megoldásért! Szépen rámutattál miért nem lehet 45 fokkal forgatni - minthogy a sarkokban csak páros számok állhatnak. (Én a tükrözésről megfeledkeztem.)
|
| Előzmény: [103] Hajba Károly, 2003-11-24 10:08:25 |
|
| [103] Hajba Károly | 2003-11-24 10:08:25 |
 Megoldás a 23. feladatra:
Legyen (S) a négyzetbe írandó számok összege és (K) az egy sor-oszlop-átló összege. Végezzük el a következő műveletet:
A két átló kétszereséhez adjuk hozzá a középső oszlop és sort és vonjuk ki belőle a szélső oszlopokat és sorokat. Így egyrészről a középső elem 6-szorosát, mésrészről 2*K-t kaptunk. Tehát a középső elem 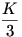 ill. ill. 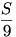 -cel egyenlő. -cel egyenlő.
A mi esetünkben a középső szám 5 és K=15. Mivel mindkét szám páratlan, így az egy sor-oszlop-átlóba írandó másik két szám vagy mindkettő páros vagy mindkettő páratlan. Továbbá az oszlopok és sorok szélső elemeinek összege páratlan, ez vagy 3 páratlan, vagy 2 páros és 1 páratlan szám összege. Ebből következik, hogy a 4 páros szám csak a sarkokba kerülhet.
A bűvös négyzetnél a nem egy sor-oszlop-átlóba írt 3 szám, mely egyéb keretfeltételeknek is megfelel, egyértelműen meghatározza a többi számot. Így a négy sarokszámot kétféle irányultsággal tudom beírni, hogy ne lehessen egymásba forgatni. Ha a tükrözéssel kialakult állapotot is azonosnak tekintjük, csak egy megoldás létezik. Tehát a megoldás az alábbi és a tükörképe:
Hajba Károly
|
| Előzmény: [102] lorantfy, 2003-11-23 09:15:26 |
|
| [102] lorantfy | 2003-11-23 09:15:26 |
 23.a) feladat Írd be az 1,2,3,4,5,6,7,8,9 számokat egy 3x3 bűvös négyzetbe!
(Úgy, hogy a sorok, oszlopok és átlók összege is azonos legyen.)
| .... |
. |
. |
| . |
.... |
. |
| . |
. |
.... |
|
23.b) feladat Hányféle beírás lehetséges, ha az egymásba forgathatókat nem tekintjük különbözőnek?
(Elemi forgatás (45 fok): amikor a főátló (....) oszlopba, a másik sorba megy át.)
|
|
| [101] Hajba Károly | 2003-11-21 13:46:46 |
 Kedves Lajos!
A pozitív egész számok tartományában értelmeztem és a 2. sor első számának 1-gyel kell kezdődnie és legalább 2 jegyű. Továbbá mind a 8 összeg egyenlő.
László pontosítása után természetesen csak egy létezik. A középső száma: 107, összege: 321
Hajba Károly
|
| Előzmény: [99] Lóczi Lajos, 2003-11-21 11:06:19 |
|
| [100] lorantfy | 2003-11-21 11:28:15 |
 Kedves Lajos és Károly!
Elnézést, de elfelejtettem írni a BŰVÖS NÉGYZET-hez, hogy a pontok csak helykitöltő szerepet játszanak, különben összeesik a TeX tábla. Szóval gondom volt az üres rekeszekkel és így tudtam gyorsan megoldani. A beírt számok: 1, 19, 98. (Az 1 számjegy mellett szintén csak "helynövelő" a pont.)
|
| Előzmény: [99] Lóczi Lajos, 2003-11-21 11:06:19 |
|
| [99] Lóczi Lajos | 2003-11-21 11:06:19 |
 Kedves Onogur!
Attól függ, hogyan értjük a kérdést.
Pontosan milyen feltételekkel kaptál kilenc megoldást? Gondolom, a négyzet sor- és oszlopösszegei ugyanaz a szám, de a fő- és mellékátlók összege is ez? A pontok egy számjegyet jelölnek? Negatív értékek megengedettek?
|
| Előzmény: [98] Hajba Károly, 2003-11-21 10:21:01 |
|
|
| [97] SchZol | 2003-11-20 16:23:38 |
 Kedves Suhanc!
Igen a nehezítésben meghagytam a feltételt, és van rá megoldásom! Egyébként, ha benézel a Biliárdgolyók és más méricskélős feladatok című téma alá, ott megtalálod Lorantfy megoldását.
Üdv, Zoli
|
| Előzmény: [96] Suhanc, 2003-11-20 14:54:09 |
|
| [96] Suhanc | 2003-11-20 14:54:09 |
 Üdvözlet! Ha jól láttam, a 15. feladatra még senki nem írt megoldást. Van egy ötletem, de az megszegi azt a kikötést,ami még az 5. feladatban szerepelt, névszerint: minden ládában 1000 pénzérme van. Sch Zolitól kérdezném: a nehezítésben meghagytad ezt a feltételt? Ha igen, van megoldásod rá?
|
|
| [95] lorantfy | 2003-11-19 22:39:21 |
 Egy könnyed kis feladat. A 7. osztályos fiamnak volt valamelyik versenyen.
Töltsétek ki a bűvös négyzetet!
|
|
|




 A.
A.  A=23 4093 8779
A=23 4093 8779 


 . Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor
. Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor 

