|
|
| [1205] Lóczi Lajos | 2006-03-19 22:43:26 |
 Erről jut eszembe a következő
223. feladat. Számítsuk ki az
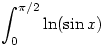
integrált.
|
|
|
| [1203] lorantfy | 2006-03-19 16:00:42 |
 222. feladat: Számítsuk ki a következő határozott integrál értékét:
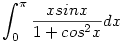
|
|
| [1202] lorantfy | 2006-03-19 15:55:20 |
 221. feladat: Oldjuk meg a p3+3p=7x+3 egyenletet, ahol p prímszám és az x egész szám.
(Műszaki főiskolák Hajós György matematika versenye 2003.)
|
|
| [1201] lgdt | 2006-03-18 20:27:57 |
 úgy látom, senkit sem hozott lázba a feladat, pedig érdekes. :-/ leírom a megoldást.
1. ki lehet nyírni, mert Zk (a k-dimenziós egész koordinátájú vektorok halmaza, ezek lehetnek a bolha stratégiái) és N között van egyértelmű megfeleltetés, és minden lövéssel ki tudunk zárni egy vektort, ha az n-edik másodpercben az n-edik vektor n-szeresére lövünk.
2. ki lehet nyírni, mert a stratégiák számegyeneséről az n-edik csapással egy 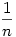 hosszúságú intervallumot zárunk ki, és hosszúságú intervallumot zárunk ki, és 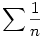 nem konvergens. nem konvergens.
3. megúszhatja, mert a stratégiák síkjáról az n-edik csapással egy  nagyságú területet zárunk ki, és nagyságú területet zárunk ki, és 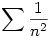 konvergens. konvergens.
|
| Előzmény: [1183] lgdt, 2006-03-10 19:19:16 |
|
|
|
|
| [1197] ágica | 2006-03-15 16:34:26 |
 :)
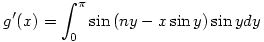
ez parciálisan integrálva:
![[-\cos{y}\sin{(ny-x\sin{y})}]_0^{\pi}+\int_0^{\pi}(n-x\cos{y})\cos{(ny-x\sin{y})}\cos{y}dy](keplet.cgi?k=D61818F66E3A6DE8)
itt az első tag nulla, a második tagot pedig felbonthatjuk két integrál különbségére:
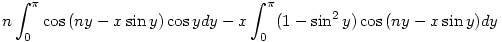
ennek második tagját még tovább bontva kapjuk:
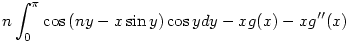
szorozzuk végig x-szel az egyenletet:

az integrálos tagról könnyen belátható, hogy n2g(x)-el egyenlő, ugyanis:
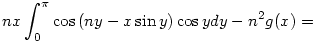
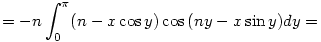
![=-n[\sin{(ny-x\sin{y})}]_0^{\pi}=0](keplet.cgi?k=7AA6A076AEE94EA3)
innen pedig már csak át kell rendezni.
Egyébként, lehet hogy hülye kérdés, de mi indokolta a Bessel-függvények definiálásakor azt az 1/ -s szorzót? (Mondjuk gondolom más "hasznuk" is van azon túl, hogy többek között ők is megoldják ezt a differenciálegyenletet.:) -s szorzót? (Mondjuk gondolom más "hasznuk" is van azon túl, hogy többek között ők is megoldják ezt a differenciálegyenletet.:)
|
| Előzmény: [1193] Lóczi Lajos, 2006-03-14 23:38:41 |
|
| [1196] qer | 2006-03-15 16:13:23 |
 219.feladatra:
Ez csak egy sejtés, de talán jó. k=1,2,3-ra (szerintem érdektelen) de nyílván jó a gömbfelület. k=4-re is a gömbfelület jön ki, elég egy tetraédert vizsgálni. k=5,6,... értékekre szerintem egy egyoldalú rendre 0,-2,... Euler-karakterisztikájú felület a megfelelő.
|
| Előzmény: [1187] Csimby, 2006-03-13 19:56:42 |
|
| [1195] qer | 2006-03-15 14:43:59 |
 218.feladatra: Először is legyen F egy tetszőleges felület, és  (F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy (F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy  (gömbfelület)=2. (gömbfelület)=2.
Ezután vizsgáljuk a körlap Euler-karakterisztikáját. Ez nyílván egy pontból, egy hurokélből és egy lapból áll, azaz  (körlap)=1-1+1=1.Az könnyen látható, hogyha egy gömbfelületből kivágunk egy körlapot, akkor egy másik körlap marad. (körlap)=1-1+1=1.Az könnyen látható, hogyha egy gömbfelületből kivágunk egy körlapot, akkor egy másik körlap marad.
Tórusz Euler karakterisztikáját (azaz k=1 esetre a kérdésre a választ) ugyanúgy számíthatjuk ki mint a körlapnál, azaz keresünk (egy lehetőleg minél egyszerűbb) felbontást. Vegyünk egy tóruszt, húzzunk be egy délkört, majd ottt vágjuk szét, de jegyezzük meg, hogy azok összetartoznak. Ha kiegyenesítjük, akkor egy hengerpalástot kapunk. Itt egy "magasság" mentén vágjuk szét a felületet, és ha kiegyenesítjük, akkor egy téglalapot kapunk, ahol a szemközti élek összetartoznak (azaz képzeletben összeragasztjuk őket). A két él egy pontban metszi egymást. Így  (tórusz)=1-2+1=0. (tórusz)=1-2+1=0.
Hogy meghatározhassuk más k-ra is az értéket, először is vegyünk egy tetszőleges F felületet, majd vágjunk ki belőle egy körlapot, vizsgáljuk, hogyan változik az Euler-karakterisztikája. Nyílván, ha egy lapot távolítunk (ami olyan mintha egy körlapot), akkor eggyel kevesebb lapja lesz az F felületnek, azaz l helyett l-1-et kell venni, azaz eggyel csökken az Euler-karakteriszika.
Ha két felület adott (mondjuk F és G), mindkettőből eltávolítunk egy-egy körlapot, majd a körlapon úgy veszünk fel csúcsokat, hogy mindkettőn ugyanannyi számú legyen (ez nyílván nem változtatja meg az Euler-karakterisztiká, mivel egy új ponttal egy új él is keletkezik), és a csúcsokat és az éleket összeragasztjuk, akkor a keletkező felület Euler-karakterisztikája egyenlő lesz  (F)+ (F)+ (G)-2-vel. (G)-2-vel.
Tórsuz úgy kapunk ha egy gömböt és tóruszt összeragasztunk, így  (k=1)=2+0-2=0 (persze ez nem újdonság,az eredmény az lett, amit vártunk). k=2 eset a k=1-re kapott felületből származik, ha még egy tóruszt ragasztunk hozzá, így (k=1)=2+0-2=0 (persze ez nem újdonság,az eredmény az lett, amit vártunk). k=2 eset a k=1-re kapott felületből származik, ha még egy tóruszt ragasztunk hozzá, így  (k=2)=0+0-2=(2+0-2)+0-2=2-2*(-2)=-2. Folytatva, tetszőleges k-ra, azt kapjuk, hogy (k=2)=0+0-2=(2+0-2)+0-2=2-2*(-2)=-2. Folytatva, tetszőleges k-ra, azt kapjuk, hogy  (k)=2-2k. (k)=2-2k.
|
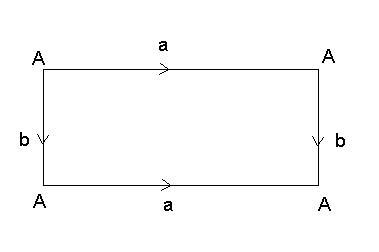 |
| Előzmény: [1187] Csimby, 2006-03-13 19:56:42 |
|
| [1194] Lóczi Lajos | 2006-03-14 23:58:40 |
 Valóban, úgy tűnik, Volterra csinált először ilyet Riemann integrálra (ami után persze adtak később egyszerűbb példákat is). A konstrukció lényege, hogy a korlátos derivált (mértékelméleti szempontból) túl sok helyen szakad: egy "kövér" Cantor-halmazon, az ilyeneket pedig Riemann nem tudja visszaintegrálni.
A feladatban viszont nem mondtam meg, milyen integrált használjunk.
220. feladat. U. az, mint a 217. feladat, csak az integrált értsük Lebesgue értelemben.
Ez a feladat jóval könnyebb, mint a Riemannos megfelelője, és az előzetes integrálos kérdések pont ezt készítették elő.
Fontos adalék, hogy Lebesgue (1900-as évek eleje) után fél évszázaddal kidolgozták a Henstock-Kurzweil integrált, amelynek definíciója formailag alig különbözik Riemannétól, és azzal a jó tulajdonsággal bír, hogy minden [a,b] intervallumon értelmezett deriváltat vissza tud integrálni (tehát a 217. feladatbeli formulában mindig egyenlőség áll), sőt egyúttal minden, [a,b]-n Lebesgue-integrálható függvényt is tartalmaz. Ezt az integrálfogalmat nyugodtan lehetne Riemann helyett tanítani, mert a bizonyítások csak alig bonyolultabbak és cserébe sokkal többet kapunk.
|
| Előzmény: [1191] nadorp, 2006-03-14 20:43:23 |
|
|
| [1192] ágica | 2006-03-14 22:50:28 |
 Vagy pedig, mivel g(x) csupán egy 1/ -s szorzóban különbözik az n-edik Bessel-függvénytől, melyre szintén teljesül ugyanez a differenciálegyenlet, így megoldható a feladat a Bessel-függvényekre vonatkozó bizonyítással teljesen analóg módon is (g(x) deriváltját számolva, majd parciálisan integrálva egy kis alakítgatás után kijön az egyenlet). -s szorzóban különbözik az n-edik Bessel-függvénytől, melyre szintén teljesül ugyanez a differenciálegyenlet, így megoldható a feladat a Bessel-függvényekre vonatkozó bizonyítással teljesen analóg módon is (g(x) deriváltját számolva, majd parciálisan integrálva egy kis alakítgatás után kijön az egyenlet).
|
| Előzmény: [1189] Lóczi Lajos, 2006-03-13 22:50:30 |
|
| [1191] nadorp | 2006-03-14 20:43:23 |
 Két helyen is találtam példát, mindkettő Volterra konstrukcióját közli. Azt látja be, hogy létezik olyan [0,1]-en mindenhol differenciálható függvény, melynek derivált függvénye korlátos, de nem Riemann integrálható.
|
| Előzmény: [1188] Lóczi Lajos, 2006-03-13 22:41:14 |
|
|
| [1189] Lóczi Lajos | 2006-03-13 22:50:30 |
 A deriválásokat elvégezve, ebben a feladatban nyilván csak annyit kell bizonyítani, hogy az y-szerinti integrálja 0-tól  -ig az alábbi kifejezésnek -ig az alábbi kifejezésnek
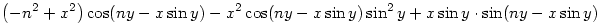
éppen nulla, ha n egész szám és x valós szám.
|
| Előzmény: [1184] Lóczi Lajos, 2006-03-10 23:10:59 |
|
| [1188] Lóczi Lajos | 2006-03-13 22:41:14 |
 Trükkös. Akkor a következő kérdés természetesen az, hogy
Van-e példa vajon olyan F függvényre, ami a zárt [0,1] intervallumon mindenhol értelmezve van, mindenhol deriválható, de az idézett Newton-Leibniz-formula nem igaz rá?
|
| Előzmény: [1186] ágica, 2006-03-13 19:39:06 |
|
| [1187] Csimby | 2006-03-13 19:56:42 |
 218. feladat Az Euler-féle poliéder-tétel ugyenbár csak "nem lyukas" testekre igaz. Hogy-néz ez ki "k lyukú testek" (k=1: tórusz, k=2: kengyel-felület) esetében?
219. feladat Adott a gömbön egy térkép országokkal és a fővárosaikkal. Vegyük azt a gráfot, aminek csúcsai a fővárosok, és két csúcsot pontosan akkor kötünk össze, ha a nekik megfelelő fővárosok országai határosak. Mondjunk olyan testet minden k-ra, hogy a testre lehessen olyan térképet rajzolni, amihez az előbbi módon definiált gráf a teljes k csúcsú gráf.
|
|
|
| [1185] Lóczi Lajos | 2006-03-12 01:59:04 |
 217. feladat. Adjunk példát (ha van) olyan F valós függvényre, amely deriválható az egész (0,1) intervallumon, de 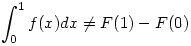 , ahol f=F'. , ahol f=F'.
|
|
| [1184] Lóczi Lajos | 2006-03-10 23:10:59 |
 216. feladat. Legyen n egész szám, x pedig valós szám. Igazoljuk, hogy az
x2g''(x)+xg'(x)+(x2-n2)g(x)=0
(differenciál)egyenlet egy megoldása a
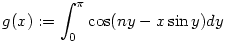 függvény. függvény.
|
|
| [1183] lgdt | 2006-03-10 19:19:16 |
 1. egy koordinátarendszerben egy láthatatlanul kicsi bolha minden másodperc elején mindig ugyanazzal az egész koordinátájú vektorral ugrik odébb (az origóból indul). tetszőleges egész koordinátájú pontjára lőhetsz minden másodperc végén.
2. a számegyenesen az origóból kiindulva mindig ugyanakkora valós számmal ugrik odébb. egy egységnyi szélességű vonalzóval csapkodhatsz minden ugrás után.
3. a síkon az origóból indulva mindig ugyanazzal a valós koordinátájú vektorral ugrik odébb, és egy négyzet alakú pecsét áll a rendelkezésedre.
Melyik esetben tudod kinyírni a bolhát és ha igen, hogyan?
Sorry a megfogalmazásért, valahogy így hangzott el előadáson is. Esetleg valaki átfogalmazhatná.
|
|





 -x helyettesítést. Ekkor egy egyenletet kapunk az ismeretlen integrálra, ahol szerepelni fog egy másik integrál is, ami azonban elemien kiszámolható (egy arkusz tangenses összetettfüggvény-derivált). A végeredmény:
-x helyettesítést. Ekkor egy egyenletet kapunk az ismeretlen integrálra, ahol szerepelni fog egy másik integrál is, ami azonban elemien kiszámolható (egy arkusz tangenses összetettfüggvény-derivált). A végeredmény: 

 -ig 1 legyen.
-ig 1 legyen. (F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy
(F)=c-e+l (ahol c a felületen lévő csúcsok, e az élek, l a lapok száma). Nevezzük ezt mondjuk Euler-karakterisztikának. Az Euler-féle poliédertétel nyílván azt jelenti, hogy 
