|
| [1297] lorantfy | 2006-07-05 23:23:32 |
 Szia Suhanc!
Kösz a megoldást! Valóban az ismétlés nélküli és az ismétléses kombináció tipikus esetei ezek a példák, csak erre nem olyan könnyű rájönni.
Még a 233. feladat maradt állva, de Sirpi [1289] segítségével remélem erre is vállalkozik valaki!
|
| Előzmény: [1296] Suhanc, 2006-07-05 22:33:44 |
|
| [1296] Suhanc | 2006-07-05 22:33:44 |
 Kedves László!
Ha nem olvastam figyelmetlenül a hozzászólásokat, a 234.feladat még él. Egy lehetséges megoldás:
a)Tegyük fel, hogy valaki odaad nekünk 6 különböző számjegyet, azzal a kéréssel, csináljunk belőle az a)-nak megfelelő hatjegyű számot. Ekkor a legkisebb számjegyet írjuk előre, utána a második legkisebbet... azaz, e 6 számjegyből pontosan egy, a feladat feltételeinek megfelelő szám készíthető. Azt kell még eldöntenünk, hány ilyen számjegyhatos választható ki. A számjegyeknek a szigorú monotonitás miatt kell különbözőeknek lenniük, és 0 nem szerepelhet közöttük, hiszen azt csak a legelső helyre írhatnánk, de 0-val nem kezdünk számot. Így 9 számjegyből kell 6 különbözőt kiválasztanunk. Ez 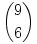 féleképp tehető meg. féleképp tehető meg.
b) A feladat az a)-hoz hasonló, de itt "csak" monotonitás az elvárt, így azonos számjegyek is lehetnek, ám 0 itt sem. Tehát itt 9 számjegyből ismétléssel kell kiválasztanunk 6-ot. Az ismert módon ez 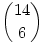 féleképp tehető meg. féleképp tehető meg.
|
| Előzmény: [1283] lorantfy, 2006-06-21 09:41:24 |
|
| [1295] Suhanc | 2006-07-05 19:47:19 |
 Kedves Tibi!
Egy lehetséges megoldás a feladatodra:
Írjuk az egyenlőtlenség jobb oldalán az 1-ek helyére a+b+c+d-t:
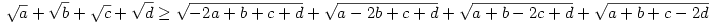
Legyen most
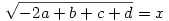
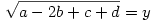
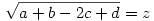
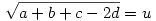
Ekkor:
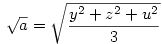
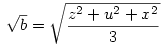
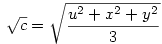
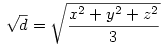
A bizonyítandó egyenlőtlenség ekkor:
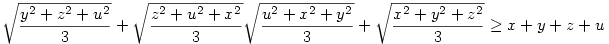
Nyilvánvaló, hogy x,y,z,u  0 . A bal oldalon a tagokat négyzetes-számtani közepekel becsülve épp a bizonyítandó állítást kapjuk. 0 . A bal oldalon a tagokat négyzetes-számtani közepekel becsülve épp a bizonyítandó állítást kapjuk.
Egyenlőség x=y=z=u esetén lehetséges, melyből a=b=c=d szükséges és elégséges feltétel levezethető.
|
| Előzmény: [1294] lorytibi, 2006-07-04 20:18:29 |
|
| [1294] lorytibi | 2006-07-04 20:18:29 |
 Sziasztok!
Matektáborban voltam a múlt héten és van egy példa, amit nem tudtunk megoldani:
236. feladat: Bbh., ha ![a,b,c,d \in \Big[0;\frac13 \Big]](keplet.cgi?k=D04D688A33348BD6) és a+b+c+d=1, akkor és a+b+c+d=1, akkor
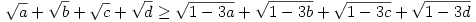
|
|
|
| [1292] lorytibi | 2006-06-24 16:50:54 |
 235.feladat megoldása: Egy konvex kilencszögnek 27 átlója van. Mivel nincs két párhuzamos átló, ezért ha az átlókat az egyik metszéspontba toljuk, akkor 54 félegyenes indul ki a pontból, 54 szöget alkotva. Így a szögek átlaga 360°/54, ami biztosan kisebb 7°, tehát biztosan van két olyan átló, melyek egyenesei 7°-nál kisebb szöget zárnak be.
|
| Előzmény: [1291] nadorp, 2006-06-23 08:34:47 |
|
| [1291] nadorp | 2006-06-23 08:34:47 |
 Egy kis ujjgyakorlat.
235.feladat Egy konvex kilencszögnek nincs két párhuzamos átlója. Bizonyítsuk be, hogy van olyan két átló, melyek egyenesei 7o-nál kisebb szöget zárnak be.
|
|
| [1290] Yegreg | 2006-06-21 23:17:56 |
 És így nyilván, ha n relatív prím 10-hez, akkor van csupa 1-esből álló többszörös. Lehet kicsit általánosítani:
pl.: milyen n számokra létezik n-nek olyan többszöröse, mely k-s számrendszerben csak m-es jegyeket tartalmaz? (0<m<k nyilván)
|
|
|
|
| [1287] lorantfy | 2006-06-21 14:26:28 |
 Kedves Jónás és Sirpi!
Kösz a megoldásokat! A 232-est kilőttétek. Végülis, ha valaki rátalál a 7 -re az már jó megoldás, de jobb a lánctörtes, én meg a skatulyásra gondoltam. -re az már jó megoldás, de jobb a lánctörtes, én meg a skatulyásra gondoltam.
|
| Előzmény: [1286] Sirpi, 2006-06-21 12:56:20 |
|
|
| [1285] jonas | 2006-06-21 12:32:05 |
 Amúgy az egysorost szinte szó szerint fel lehet olvasni:
| +/ |
Hány olyan dolog van, aminek |
| *./"1 |
minden |
| 2v\"1 |
két szomszédos része |
| ahol v =. <:/ |
helyesen rendezett, |
| (6$10)#: |
ha hat tizes számrendszerbeli számjegyre bontjuk |
| i.1e6 |
a számokat egymillióig? |
|
|
| Előzmény: [1284] jonas, 2006-06-21 12:24:22 |
|
| [1284] jonas | 2006-06-21 12:24:22 |
 232. feladatra: 7 =21.9911. Egyébként ez az egyetlen. Lánctörtté bontásból is megkapható (3/1, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532 stb az első közelítések), de úgy is, hogy mind a százat végigpróbáljuk. =21.9911. Egyébként ez az egyetlen. Lánctörtté bontásból is megkapható (3/1, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532 stb az első közelítések), de úgy is, hogy mind a százat végigpróbáljuk.
234. feladatra: Nem lövöm le a számokat, de a 31-es osztási maradékuk 24 (a szigorúan monoton esetben), ill 14 (a monoton esetben). Szintén meg lehet oldani okosan, vagy végigpróbálgatással.
Az ilyen próbálgatásokra, mint az előző kettő, elég hasznos a J programozási nyelv. Komoly programok írására nekem nem alkalmas, de az ilyen egyszerű matematikai számításokat sokkal könnyebben el lehet vele végezni, mint bármilyen más számológép jellegű interpreterrel. A 234. feladatot is két sorban meg lehet vele oldani. A megoldásom (MIME-Base64-enkódolva, mivel ebbe a fórumba nem lehet rendesen kódot beírni):
Ky8qLi8iMV0yPC9cIjEoNiQxMCkjOmkuMWU2CisvKi4vIjFdMjw6L1wiMSg2
JDEwKSM6aS4xZTY=
Ennek a kikódolását kell beilleszteni az interaktív interpreterbe, hogy megkapjuk a két eredményt.
|
| Előzmény: [1283] lorantfy, 2006-06-21 09:41:24 |
|
| [1283] lorantfy | 2006-06-21 09:41:24 |
 232. feladat: Bbh. a  ,2 ,2 ,3 ,3 ...100 ...100 számok között van olyan, amely egy egész számtól 0,01-nál kevesebbel tér el! számok között van olyan, amely egy egész számtól 0,01-nál kevesebbel tér el!
233. feladat: Bbh. minden n poz. egész számhoz létezik olyan k poz. egész szám, hogy az nk szorzat tízes számrendszerbeli alakja csak 1-es és 0 számjegyeket tartalmaz!
234. feladat: Hány olyan tízes számrendszerbeli hatjegyű szám van melynek számjegyei balról jobbra haladva,
a) szig. mon. növekednek?
b) mon. mövekednek?
|
|
|
| [1281] jonas | 2006-06-19 11:54:27 |
 Itt vannak a következő hasonló sorozatok (az összes 100000 alatti):
199 409 619 829 1039 1249 1459 1669 1879 2089
34913 37013 39113 41213 43313 45413 47513 49613 51713 53813
52879 53299 53719 54139 54559 54979 55399 55819 56239 56659
30427 35257 40087 44917 49747 54577 59407 64237 69067 73897
28549 36319 44089 51859 59629 67399 75169 82939 90709 98479
|
| Előzmény: [1280] jonas, 2006-06-19 11:51:51 |
|
| [1280] jonas | 2006-06-19 11:51:51 |
 Kipróbáltam, és 3000-ig csak ez az egy van. Mivel a különbség 210 többszöröse kell, hogy legyen, veszem az összes számtani sorozatot, aminek a differenciája 210 vagy pozitív többszöröse, prímszámtól indul, és a legnagyobb tagja 3000 alatt van. Ilyan sorozatból 186 van. Szűrve azokat, amelyeknek minden tagja prím, csak egy marad: 199 409 619 829 1039 1249 1459 1669 1879 2089.
|
| Előzmény: [1279] jonas, 2006-06-19 11:38:38 |
|
| [1279] jonas | 2006-06-19 11:38:38 |
 Feltételezem, hogy a konstans számtani sorozat ki van zárva.
A Szalay Számelmélet könyv az 1.5 fejezetben megadja a következő példát: 210k+199 ahol 0 k k 9. Könnyen ellenőrizhető, hogy ez valóban jó példa. Hogy több van-e, annak nem számoltam utána. 9. Könnyen ellenőrizhető, hogy ez valóban jó példa. Hogy több van-e, annak nem számoltam utána.
Segíthet, hogy a különbségnek biztosan oszthatónak kell lennie minden 10-nél kisebb vagy egyenlő prímszámmal, mert különben az adott prímszám valamelyik tagot biztosan osztja.
|
| Előzmény: [1278] lindus, 2006-06-19 11:08:11 |
|
| [1278] lindus | 2006-06-19 11:08:11 |
 Sziasztok! Tudnátok segíteni? :-)) A feladat: keresni kellene tíz 3000-nél kisebb prímszámot ami számtani sorozatot alkot. Valahol a neten nem tudtok prímszámok gyüjteményét? Köszi....
|
|
| [1277] Iván88 | 2006-06-15 20:51:26 |
 Ez nem annyira matekfeladat, de nem akartam csak ezért új témát indítani.
Lázasan keresek egy könyvet; ANDRÁSFAI BÉLA: ISMERKEDÉS A GRÁFELMÉLETTEL c. könyvét(nekem megvolt, de sajnos elvesztettem, és kéne egy ilyen) Azt szeretném kérdezni, hogy van e valakinek a birtokában ilyen, és ha igen, akkor -némi ellenérték fejében- odatudná adni? Vagy tudja valaki, hogy hol llehet kapni ilyet? Köszönettel: Gresits Iván
|
|
| [1276] epsilon | 2006-06-10 10:16:53 |
 Pontosítás: 0<a<=e helyett 1<a<=e kell!
|
|
| [1275] epsilon | 2006-06-10 10:14:46 |
 A feladat még annyiban általánosítható, hogy n>1 pozitív egész helyett x>0, továbbá 1 helyett b>0 tehető, és ekkor, ha a>e (a 2,71... Euler-féle állandó) akkor marad a két kifekezés közötti egyenlőtlenség, és megfordul, ha 0<a<=e. (Az egészset valójában függvénymonotonítással, a deriválttal könyű belátni).
|
|
| [1274] epsilon | 2006-06-09 08:53:43 |
 A feladatnak egy általánosítása az előző módszerrel is könnyűszerrel bizonyítható, de még egy másik ötlettel egyben általánosítva: ha a>1 és n>1 pozitív egész szám, akkor:
|
 |
|





 0 . A bal oldalon a tagokat négyzetes-számtani közepekel becsülve épp a bizonyítandó állítást kapjuk.
0 . A bal oldalon a tagokat négyzetes-számtani közepekel becsülve épp a bizonyítandó állítást kapjuk. 



 -re az már jó megoldás, de jobb a lánctörtes, én meg a skatulyásra gondoltam.
-re az már jó megoldás, de jobb a lánctörtes, én meg a skatulyásra gondoltam. k
k
