| [131] Gyuri | 2003-12-03 00:29:47 |
 31. feladat: rabok sapkai 2
Bizonyara ez is sokak altal ismert, de igencsak passzol ide.
A bortonorok unalmukban, vagy talan a kozelgo Karacsonyra valo tekintettel egy jatekot eszelnek ki az intezmenyben sinylodo 100 embertarsuk szamara. Igy hangzik a jatekra valo felhivas: Holnap sorba allitunk benneteket, mindenki csak az elotte allokat fogja latni. Mindenki kap a fejere egy-egy sapkat is, mely vagy feher vagy fekete lesz. Mindenki csak egyszer szolalhat meg, es csak e ket szin egyiket mondhatja. Ahanyan eltalajak a fejukon levo szint, szabadok. Mit javasoljunk a szerencsetleneknek, ha a biztosan megszabadulok szamat akarjuk maximalizalni?
Udv: Gyuri
|
|
| [130] Hajba Károly | 2003-12-03 00:07:57 |
 Kedves László!
Nem veszünk össze a 29-es számon, s hogy félreértés se essen belőle, gyorsan megoldom. :o)
a)
Ha (1) és (2) fehér sapkát viselt volna, (3) azonnal szólna: én fekete vagyok.
Mivel (3) nem szól azonnal, így (1) és (2) is tudja, hogy nem lehetnek mindketten fehérek. Mivel (2) látja a fehér sapkát, ő csak fekete lehet és a biztos információ tudatában szól: én fekete vagyok és szabad.
Ha (1) fekete lenne, (2) nem lenne biztos információ tudatában és nem szólna. Mivel mégis szólt és nem vitték vissza a cellába, (1) tudja, hogy ő fehér és szól: én fehér vagyok, de elkéstem.
Mivel (3) nemszólalásából csak (1) és (2) kapott számukra nem ismert információt, így szegény (3) hoppon maradt új információ terén. Az ő esélye 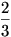 a feketére és a feketére és 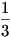 a fehérre. Így (3) nem tippel. a fehérre. Így (3) nem tippel.
b)
(1)-nek 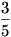 esélye van a fekete sapkára, így visszaviszik dupla büntetéssel. (2)-nek esélye van a fekete sapkára, így visszaviszik dupla büntetéssel. (2)-nek 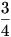 esélye van a feketére és kiszabadul. (3)-nak esélye van a feketére és kiszabadul. (3)-nak 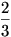 esélye van a fekete sapkára, de későn jutott szóhoz. esélye van a fekete sapkára, de későn jutott szóhoz.
Üdv: HK
|
| Előzmény: [128] lorantfy, 2003-12-02 21:42:13 |
|
| [129] lorantfy | 2003-12-02 22:50:07 |
 Kedves Károly!
Most veszem észre, hogy rosszul számoztam az előző feladatot és így „felülírtam” a Te példádat. Most beírok egy megoldást és majd egyezkedünk a 29-es számon.
Egy személynek 2 nagymamája, 2 nagyapja, 4 dédmamája és 4 dédapja van a családfán.
29.a) Nagymamáink dédapjai: 2 nagymamánknak összesen 8 dédapja van.
Dédmamáink nagyapjai: 4 dédmamánknak összesen 8 nagyapja van.
29.b) Összesen persze nem 16-an vannak, mert közöttük van 4 azonos személy.
A nagymamák édesanyjai dédmamák, így a nagymamák anyai ágon vett dédapjai egyben a dédmamák nagyapjai. Ők nagymamánként ketten vannak, összesen négyen.
Tehát a nagymamáink dédapjai és a dédmamáink nagyapjai összesen 12-en vannak
|
| Előzmény: [121] Hajba Károly, 2003-12-01 11:35:26 |
|
| [128] lorantfy | 2003-12-02 21:42:13 |
 Kedves Károly!
Nagyon tetszik a megoldás „előadása”. Én is be akartam írni, de így nem sikerült volna.
Mondok inkább egy másik feladatot, ami erről jutott eszembe:
29. feladat:
Karácsonykor a börtönigazgató, aki nagyon szereti a logikai feladatokat magához rendeli a három legdörzsöltebb rabot. Sorba állítja őket egymás után és mutat nekik 5 sapkát, 3 fekete színűt és 2 fehéret és ezt mondja nekik: - Most bekötöm a szemeteket és mindegyikőtök fejére felteszek egy sapkát az 5 közül. A maradék sapkákat elteszem, majd leveszem a kötést a szemetekről. Aki először megmondja milyen sapka van a saját fején, az kiszabadul. Aki viszont rosszat mondana, annak megduplázom a büntetését.
Kérdés: Mennyi az egyes rabok kiszabadulásának valószínűsége? Ha:
a): A rabok nagyon unják már a börtönt, így nem kockáztatják meg a dupla büntetést!
b): A rabok tippelnek, de csak akkor, ha 50 %-nál nagyobb ez esélye, hogy a tipp bejön. Itt a rabok a sorszámuk sorrendjében szólalhatnak meg. A rosszul tippelő rab visszamegy a cellájába, a másik kettő (a tippelés eredményét ismerve) tovább játszik.
(Az első rab nem látja a másik kettőt. A középső látja az első sapkáját. A hátsó látja mindkét előtte álló sapkáját. (A saját sapkáját egyik sem látja!)).
|
 |
| Előzmény: [127] Hajba Károly, 2003-12-02 01:19:59 |
|
| [127] Hajba Károly | 2003-12-02 01:19:59 |
 Kedves Gyuri!
Ez egy igazi érdekes matekfeladat, gratula! Legyen  , aki a szorzatot látja, és , aki a szorzatot látja, és  , aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk. , aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk.
1)
 : [Többféleképpen tudom a számot szorzattá bontani,] nem tudom. : [Többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom. 1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   2, 3, 4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom. 2, 3, 4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, továbbá : [Mivel nem tudja, továbbá   4; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom. 4; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, továbbá : [Mivel nem tudja, továbbá   5; s mivel 5; s mivel  =6 egyik tagjához tartozó összeget kizártuk,] tudom. =6 egyik tagjához tartozó összeget kizártuk,] tudom.
 : [Mivel tudja, : [Mivel tudja,  =6, s mivel =6, s mivel  =7,] tudom. =7,] tudom.
A=1, B=6
2)
 : [Többféleképpen tudom a számot összeggé bontani,] nem tudom. : [Többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   2, 3; többféleképpen tudom a számot szorzattá bontani,] nem tudom. 2, 3; többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   1 v. prím; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom. 1 v. prím; még mindig többféleképpen tudom a számot összeggé bontani,] nem tudom.
 : [Mivel nem tudja, továbbá : [Mivel nem tudja, továbbá   4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom. 4; még mindig többféleképpen tudom a számot szorzattá bontani,] nem tudom.
 : [Mivel nem tudja, : [Mivel nem tudja,   4, s mivel 4, s mivel  =5 egyik tagjához tartozó összeget kizártuk,] tudom. =5 egyik tagjához tartozó összeget kizártuk,] tudom.
 : [Mivel tudja, továbbá : [Mivel tudja, továbbá  =5; s mivel =5; s mivel  =6 egyik tagjához tartozó összeget kizártuk,] tudom. =6 egyik tagjához tartozó összeget kizártuk,] tudom.
A=2, B=3
Remélem, minden esetet figyelembe vettem, mivel nagyon leizzadtam. :o)
HK
|
| Előzmény: [123] Gyuri, 2003-12-01 14:32:15 |
|
|
| [125] jenei.attila | 2003-12-01 16:59:22 |
 Kedves László!
Csatlakozok Gyuri megjegyzéséhez, hozzátéve, hogy az egyenletrendszer szimmetriáját nyilván úgy értetted, hogy adott gyökök mellett ezek bizonyos permutációi is megoldást adnak. A feladatban jól látszik, hogy összesen három (az identitást is belevéve) megfelelő permutáció létezik. Ez azonban nem jelenti azt, hogy a gyökök egyenlők.
|
| Előzmény: [119] lorantfy, 2003-12-01 09:05:35 |
|
| [124] Gyuri | 2003-12-01 16:52:49 |
 28. feladat megoldasa
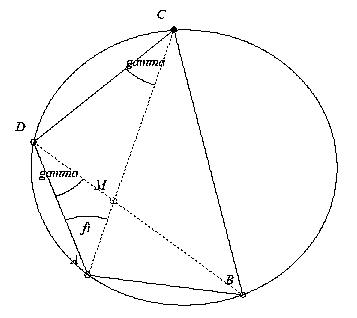
Tekintsuk a lenti abrat. Az AMB ill. az ACB  -ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD -ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD  -eket: -eket:
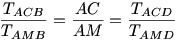
Az AB=AD=a jelolessel:
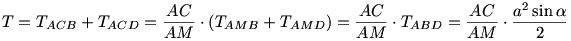
A 'gamma'-val jelolt szogek valoban egyenloek, hisz azonos hosszusagu hurokhoz tartozo keruleti szogek (megfelelo iven). Igy (az implikacio jele nem akar mukodni):
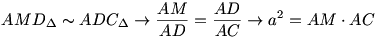
Az a2-re kapott erteket a T-re levezetett kifejezesbe irva a bizanyitando egyenloseget kapjuk.
|
 |
|
| [123] Gyuri | 2003-12-01 14:32:15 |
 Ha mar ugyis Erdekes matekfeladatok a topic, akkor talan megfelelo helyre irom le a kovetkezot.
30. feladat: Ket teljesen intelligens, es egymas eme tulajdonsagat ismero ember beszelgetnek. Egy harmadik szemely meg a tarsalgasuk elott elhelyezett ket cedulat a homlokukon. Mindket emberunk csak a masik fejen levo cedulat latja. A cedulak egyiken ket pozitiv egesz szam osszege, a masikan ugyanannak a ket szamnak a szorzata szerepel. Szerencsere annyit legalabb elarult nekik a harmadik szemely, hogy melyikuk fejen van az osszeg illetve a szorzat. Ezek utan a kovetkezokeppen tarsalognak.
-Nem tudom, mi a ket szam.
-Nem tudom, mi a ket szam.
-Nem tudom, mi a ket szam.
-Nem tudom, mi a ket szam.
-Mar tudom, mi a ket szam.
-Mar en is tudom, mi a ket szam.
Termeszetesen mas informacio nem jut el hozzajuk. Pl. nem allnak tukor elott, nem irjak le egymas szamait papirra, nem irnak emailt, stb.
Remelem mar mindenki tudja, mi a ket szam!
Udv: Gyuri
|
|
| [122] Gyuri | 2003-12-01 14:12:49 |
 Kedves Laszlo!
Ismet akadekoskodnek a 25. feladatra tett megjegyzese kapcsan. Az egyenletrendszer szimmetriaja meg nem biztositek a megoldas szimmetriajara. Legyen

ekkor az
f(x)=y,f(y)=z,f(z)=x
egyenletrendszernek megoldasa a (0,1,-1) szamharmas. De megoldas az
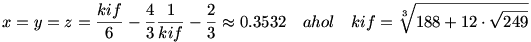
szamharmas is. Udv: Gyuri
|
| Előzmény: [119] lorantfy, 2003-12-01 09:05:35 |
|
| [121] Hajba Károly | 2003-12-01 11:35:26 |
 A következő feladaton csak annyit lehet gondolkodni, mint amennyi időt Örkény egyperceseire fordítunk. Ha valaki tovább gondokozik rajta, csal, mint Rodolfó a bűvész.
29. feladat: A) Kik vannak többen? Nagymamáink dédapjai vagy Dédmamáink nagyapjai? B) Hányan vannak összesen?
HK
|
|
| [120] nadorp | 2003-12-01 10:45:34 |
 Kedves László !
Vázolok egy megoldást a 24.b feladatra.
Legyen X=AB…BC=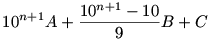 és és
Y=CB…BA=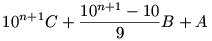
A 7-tel való oszthatóságot elég a 9X és 9Y számokra nézni. Felhasználva még azt, hogy 10 hatványai ugyanazt a maradékot adják 7-tel osztva, mint 3 hatványai, kapjuk:
7 | 2.3n+1A+3(3n-1)B+2C és 7 | 2.3n+1C+3(3n-1)B+2A
3 hatványai rendre a következő maradékokat adják 7-tel osztva: 3,2,6,4,5,1. Ezt felhasználva három esetet különböztetünk meg.
1.eset: n=6k alakú
Ekkor 7 | 3n-1 és 3n+1 7-es maradéka 3, ezért 7 | 6A+2C és 7 | 6C+2A teljesül. De ekkor véve a két szám összegét és különbségét: 7 | 4(A-C) és 7 | 8(A+C), azaz 7 | A-C és 7 | A+C. Ez csak úgy lehet, ha A és C közül az egyik 0, amit kizártunk. Ekkor tehát nincs megoldás.
2.eset: n=6k+5 alakú
Ekkor 3n 7-es maradéka 5 és 3n+1 7-es maradéka 1, ezért 7 | 2A+5B+2C vagy másképpen 7 | 2A+5B+2C-7B=2(A-B+C). Ez teljesül,ha például A=8 B=2 C=1.
3.eset: n 6k és n 6k és n 6k+5 alakú 6k+5 alakú
Mivel 7 | 9X-9Y, ezért 7 | 2(3n+1-1)(A-C) . Ez most csak úgy lehet ha 7 | A-C, azaz A=9 C=2 vagy A=8 C=1 ( vagy ha felcseréljük A és C szerepét, de az most mindegy). Látszik, hogy A C és n ismeretében B egyértelműen meghatározható mod 7. A számolást nem részletezve az alábbi két táblázatot kapjuk:
| n |
1 |
2 |
3 |
4 |
| A |
9 |
9 |
9 |
9 |
| C |
2 |
2 |
2 |
2 |
| B |
5 |
0 |
1 |
2 |
|
| n |
1 |
2 |
3 |
4 |
| A |
8 |
8 |
8 |
8 |
| C |
1 |
1 |
1 |
1 |
| B |
6 |
0 |
4 |
1 |
|
Látszik, hogy n=6k+4 esetén B megegyik A-val vagy C-vel, ami nem lehet. A feladatnak tehát n=6k vagy n=6k+4 esetén nincs megoldása, máskor mindig van.
|
| Előzmény: [110] lorantfy, 2003-11-29 00:33:28 |
|
| [119] lorantfy | 2003-12-01 09:05:35 |
 Kedves Gyuri!
Kösz a segítséget!
Ha nem tudunk a szám elejére 0-kat tenni, hát tegyünk a végére. Mig a TeX-el vacakoltam, elfelejtettem, hogy A tartalmazhat még páros kitevőjű prímtényezőket és ezzel "n" jegyűvé növelhető.
Mostmár mindegy. Lényeg az, hogy összejött a megoldás.
Ügyes a 25. feladatra adott megoldásod is. Én ott arra gondoltam, hogy mivel szimmetrikus az egyenletrendszer, a megoldás nyilván x=y=z=a. Így elegendő, ha megoldjuk a
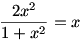
egyenletet. Amiből x(x-1)2=0 és így x=y=z=0 vagy x=y=z=1.
|
| Előzmény: [118] Gyuri, 2003-12-01 04:26:07 |
|
| [118] Gyuri | 2003-12-01 04:26:07 |
 Kedves Laszlo!
Bizonyara az ejszakazasnak tudhato be a tevesztese.
A 24.c feladathoz pont az 1. pelda szolgaltat egy megoldast:
A=(1011+1).11-2.102=82644628100.
Hasonloan megoldas meg: (1011+1).11-2.i2 a kovetkezokre: i=4,5,6,7,8,9
A teljes megoldast ilyen koran mar nincs erom leirni...
Udv: Gyuri
|
| Előzmény: [117] lorantfy, 2003-12-01 00:24:24 |
|
| [117] lorantfy | 2003-12-01 00:24:24 |
 Kedves Nádor P.!
Jó példát adtál. Remélem jó lesz a megoldás is!
Megoldás a 24.c feladatra: Eredeti szövege: Keressünk olyan A pozitív egész számot, melyre igaz, hogy önmaga után leírva még egyszer (pld A=12264 esetén 1226412264) a kapott szám négyzetszám.
Az A-ból képezett „duplázott” szám: AA=k2. Legyen A „n” jegyű szám a 10-es számrendszerben, ekkor
AA=10nA+A=(10n+1)A=k2
A (10n+1)A minden prímtényezője páros (második) hatványon van és (10n+1) A. A.
Ebből az következik, hogy 10n+1-nek tartalmaznia kell legalább egy prímtényezőt második hatványon: p12, a többi páratlan (1) kitevőjű prímtényezőt pedig az A szám is tartalmazza, igy lesz a szorzat négyzetszám. Gondolnunk kell arra is, hogy A szám n jegyű.
Gyakorlatilag: 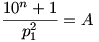 vagy 10n+1=p12A vagy 10n+1=p12A
Nézzük mi lehet ez a p1 prímtényező: 2 és 5 nyilván nem lehet, 3 és 9 nem lehet, mert a számjegyek összege 2.
Lehet 7 és 11. Többet nem is keresünk, ugyanis már ezek is túl nagyok.
Hiszen 10n+1-et 49-el vagy 121-el osztva, az A szám csak (n-1) illetve (n-2) jegyű lesz. Ami azt jelenti, hogy egy vagy két 0-t kéne elé írni, hogy „duplázáskor” a négyzetszám létrejöjjön. Ezt a feladat szövege nem engedi meg.
Így NINCS ilyen A szám!
Érthetőbbé válik a dolog, ha megnézünk egy-két példát, amikor a 0 számjegy segítségével teljesül a feltétel.
1.példa:
1011+1=112 23 4093 8779  A=23 4093 8779 A=23 4093 8779
Szorzatuk:
112 232 40932 87792
négyzetszám. A=826446281 - 9 jegyű szám, igy a szorzat: 82644628100826446281 – négyzetszám.
2.példa:
1021+1=72 11 13 127 2689 459691 909091
A=11 13 127 2689 459691 909091
Szorzatuk:
72 112 132 1272 26892 4596912 9090912
A=20408163265306122449 – 20 jegyű szám, kell elé egy 0-számjegy:
A négyzetszám: 20408163265306122449020408163265306122449
|
| Előzmény: [108] nadorp, 2003-11-28 12:24:24 |
|
| [116] Gyuri | 2003-12-01 00:12:04 |
 Kedves Zoli!
A 25. feladat megoldasa:
ha valamelyik valtozo 0, akkor a tobbi is az. tehat ha valamelyik nem 0, akkor a tobbi sem lehet az. ekkor nyilvan mindegyik pozitiv kell legyen. az egyenletek osszeszorzasabol:
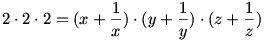
de ez csak x=y=z=1 eseten lehet, hisz a>0 eseten 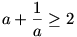 es egyenloseg csak a=1 eseten all fenn. es egyenloseg csak a=1 eseten all fenn.
igy pontosan ket megoldas van.
udv: Gyuri
|
| Előzmény: [111] SchZol, 2003-11-29 21:44:23 |
|
| [115] Hajba Károly | 2003-11-30 01:41:05 |
 Kedves Attila!
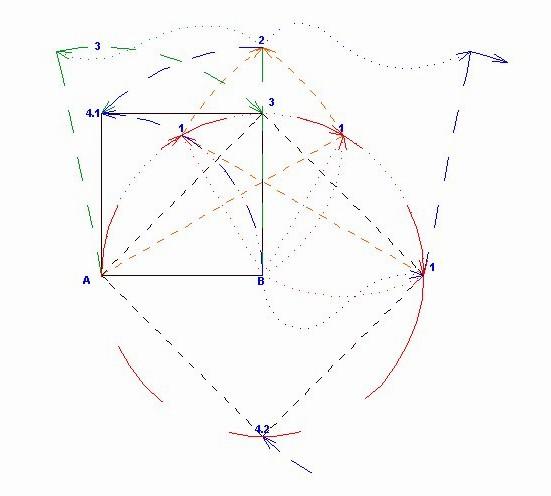
Abban igazad van, hogy mind 20. mind a 21. feladat megoldása a 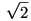 szerkesztése, de a két feladat végeredménye más. Nevezhetjük édestestvéreknek is. Az alábbi ábra mutatja a különbséget és egyben a szerkesztés egyszerűségét is. Nem kell invertálni sem. szerkesztése, de a két feladat végeredménye más. Nevezhetjük édestestvéreknek is. Az alábbi ábra mutatja a különbséget és egyben a szerkesztés egyszerűségét is. Nem kell invertálni sem.
HK
|
 |
| Előzmény: [93] jenei.attila, 2003-11-19 13:00:17 |
|
| [114] SchZol | 2003-11-29 22:07:26 |
 28.feladat: (A verseny 4. feladata)
Az ABCD húrnégyszögben AB=AD és az A csúcsnál lévő belső szög  . Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor . Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor
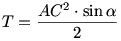
|
|
| [113] SchZol | 2003-11-29 21:55:34 |
 27.feladat: (A verseny 3. feladata)
Az egész együtthatós ax2+bx+c=0 másodfokú egyenletnek két különböző gyöke van a (0;1) nyílt intervallumban. Bizonyítsa be, hogy akkor |a| 5 5
|
|
| [112] SchZol | 2003-11-29 21:46:42 |
 26.feladat (A verseny 2. feladata)
Legfeljebb hány részre oszthatja fel a síkot, a sík egy rögzített pontján áthaladó k darab kör és n darab egyenes, ha k és n pozitív egész szám? Határozza meg a részek maximális számát megadó R(k;n) függvényt!
|
|
| [111] SchZol | 2003-11-29 21:44:23 |
 November 28-án és 29-én került megrendezésre Zalaegerszegen az Izsák Imre Gyula komplex verseny. Íme a matematika példák a versenyről:
25.feladat: (A verseny 1. feladata)
Oldja meg az alábbi egyenletrendszert a valós számhármasok halmazán:
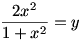
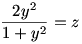
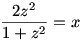
|
|
| [110] lorantfy | 2003-11-29 00:33:28 |
 Kedves Nádor P. és Károly!
Köszönet a megoldásokért! Természetesen A=0, C=0 nem megengedett, mint az az ilyen feladatoknál lenni szokott. Gyakorlatilag megvan a megoldás - persze nem ártana ha valaki szépen összefoglalná. Külön köszönet a 24.c-ért. Én úgy gondoltam a további általánosítást, hogy a "tengelyesen szimmetrikus" számok 7-tel való oszthatóságát kellene vizsgálni, csak még nem volt időm rá.
|
| Előzmény: [108] nadorp, 2003-11-28 12:24:24 |
|
| [109] Hajba Károly | 2003-11-28 13:14:36 |
 Kedves László!
A 24/a feladattal foglalkoztam egy kicsit, s mivel találtam rá példát, így a válasz: lehetséges (pl.: 168 - 861). Ha ragaszkodunk a háromjegyű számhoz, akkor |A-C|=7, tehát a számokpárok 1 és 8-cal ill. 2 és 9-cel kezdődhetnek.
(1) ABC -> 100*A+10*B+C=7*N
(2) CBA -> 100*C+10*B-C=7*M
(2)-(1) 99*(A-C)=7*(M-N)
Mivel 99 nem osztható 7-tel, továbbá M-N oszthatósága jelen esetben közömbös, így A-C mindenképpen osztható 7-tel. Ebből az is következik, hogy M-N osztható 99-cel.
Más a helyzet a 24/b feladattal. Ha a fenti levezetést minden n-re elvégezzük, találunk 7-tel osztható első számot pl.: 9009. Ekkor egyéb vizsgálatok is szükségesek, de most nincs időm rá.
HK
Ui.: A CBA egyes kis- és középboltok egyfajta országos tömörülése, felénk is van(/volt?).
|
| Előzmény: [107] lorantfy, 2003-11-28 00:45:42 |
|
| [108] nadorp | 2003-11-28 12:24:24 |
 Kedves László !
Gondolom, a 24.b feladatban a kérdést úgy értetted, hogy bármely n-re léteznek-e megfelelő A,B,C számjegyek. Én arra jutottam, hogy ha megengeded az A=0 vagy C=0 eseteket, akkor csak n=6k+4 esetén nincs megoldás, ha nem, akkor n=6k és n=6k+4 esetén nincsenek megfelelő számok. A megoldás leírásával még várnék. Viszont csatlakoznék egy hasonló feladattal:
24.c feladat: Keressünk olyan A pozitív egész számot, melyre igaz, hogy önmaga után leírva még egyszer (pld A=12264 esetén 1226412264) a kapott szám négyzetszám.
|
| Előzmény: [107] lorantfy, 2003-11-28 00:45:42 |
|
| [107] lorantfy | 2003-11-28 00:45:42 |
 24.a feladat: Legyenek ABC és CBA tizes számrendszerbeli számok, ahol A,B,C különböző számjegyeket jelölnek. Lehetséges-e, hogy mindkét szám osztható 7-tel?
24.b feladat: Legyenek ABB...BBC és CBB...BBA tizes számrendszerbeli számok, ahol "A" és "C" számjegyek között n darab "B" számjegy áll és A,B,C különböző számjegyeket jelölnek. Lehetséges-e, hogy bármely n-re mindkét szám osztható 7-tel?
Megjegyzés1: Sajnos felülvonást nem tudok húzni, ha valaki tud, kérem írja be a TeX témába!
Megjegyzés2: Mifelénk az ABC áruházakból CBA-k lesznek. Erről jutott eszembe ez a feladat.:-)
|
|






 , aki a szorzatot látja, és
, aki a szorzatot látja, és  , aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk.
, aki az összeget látja. S úgy tűnik, a végeredmény attól függ, ki kezdte a párbeszédet, mivel erről nincs infónk.  1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom.
1 v. prím; többféleképpen tudom a számot összeggé bontani,] nem tudom. 
 -ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD
-ek B-hez tartozo magassaga ill. alapegyenese kozos. Hasonloan szemlelve az AMD es ACD 
 A.
A.  A=23 4093 8779
A=23 4093 8779 

 . Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor
. Bizonyítsa be, hogy ha a húrnégyszög terültetét T jelöli, akkor