|
|
| [1513] jenei.attila | 2006-11-15 19:27:32 |
 A feladat megtalálható Lovász László Kombinatorikai problémák és feladatok c. könyvében. Itt a megoldást az ún. inverzió vektorok használatával adják meg. Egy n-ed rendű p permutáció inverzió vektora egy n elemű t vektor (tömb), amelynek j-edik eleme azt adja meg, hogy a permutációban hány előző elem kisebb, mint a j-edik elem: tj=|1<=i<j:p(i)>p(j)|, vagyis rögzített j mellet a kisebb indexekkel képezhető inverziók számát. Világos, hogy 0<=tj<=j-1, és a t elemeinek összege éppen a p inverzióinak számát adja. Fordítva is igaz: egy feltételeknek megfelelő t vektor egyértelműen meghatározza a p permutációt (ez is egy érdekes kis feladat). Ezért a k=t1,+t2+...+tn egyenlet feltételnek megfelelő (0<=tj<=j-1) megoldásait kell összeszámolni, vagyis k hányféleképpen írható fel ilyen módon n db. szám összegeként. Ennek az ún. partíciós problémának a megoldását adja a Nadorp által felírt polinom k-ad fokú tagjának együtthatója.
Erre a megoldásra gondoltál?
|
| Előzmény: [1511] Cckek, 2006-11-14 19:03:42 |
|
| [1512] nadorp | 2006-11-15 17:03:41 |
 Félek tőle, hogy erre nincs zárt formula. Ha tévedtem, akkor annál jobb. Az az erős sejtésem ( bár ez is kétséges, úgyhogy ne dobáljatok meg kővel), hogy ha a keresett számot I(n,k)-val jelöljük, akkor az
fn(x)=(1+x)(1+x+x2)...(1+x+...xn-1) polinomban xk együtthatója éppen I(n,k)
|
| Előzmény: [1511] Cckek, 2006-11-14 19:03:42 |
|
| [1511] Cckek | 2006-11-14 19:03:42 |
 Jó, részemről befejezve felejtsük el:)) Itt van egy megint csak érdekes feladat:)) Hány n-edrendű permutáció inverzióinak a száma k???
|
|
| [1510] jenei.attila | 2006-11-14 16:29:21 |
 Egyáltalán nem akartalak megsérteni, szerintem nem is volt rá okod, hogy megsértődj. A véleményemet pedig hadd mondjam már el, én teljesen jószándékúan kérdeztem, hogy mi a feladatban az érdekesség, trükk. Most, hogy már megvilágítottad a feladat hátterét, valóban érdekesebbnek találom, bár még mindíg kicsit "megcsinált" ízű. Egyébként engedd meg, hogy azzal a feladattal foglalkozzak, amelyik nekem tetszik, a versengéssel kapcsolatban meg nem értem mire gondolsz.
|
| Előzmény: [1509] Cckek, 2006-11-14 15:49:20 |
|
| [1509] Cckek | 2006-11-14 15:49:20 |
 Kedves Attila. Eddig mintha starpás és mesterkélt lett volna. hmm:) Amúgy ez csak egy feladat, kitűztem mert reméltem, hogy van akinek örömet okoz a megoldása. Ha neked nem, hát akkor ne foglalkozz vele, ez itt nem verseny, és remélem még csak versengés sem.
|
| Előzmény: [1504] jenei.attila, 2006-11-14 11:32:30 |
|
|
| [1507] jenei.attila | 2006-11-14 12:25:38 |
 Lehet, hogy erre gondolt, de ez szerintem kb. ugyanaz mint a stieltjes integrál, csak nem nevezzük nevén. Egyébként gondolom Te már előttem felismerted az integrál közelítő összeget. Te nem Stieltjes integrálra gondoltál?
|
| Előzmény: [1506] nadorp, 2006-11-14 12:19:34 |
|
| [1506] nadorp | 2006-11-14 12:19:34 |
 Szerintem Cckek arra gondol, hogy kár belekeverni a példába a Stieltjes-integrált, mert ha az eredeti szummában észrevesszük a 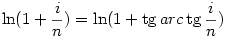 nyilvánvaló összefüggést, akkor mezei Riemann közelítő összeget kapunk, és azonnal adódik a nálam az x=tg y helyettesítés után kapott integrál. nyilvánvaló összefüggést, akkor mezei Riemann közelítő összeget kapunk, és azonnal adódik a nálam az x=tg y helyettesítés után kapott integrál.
|
| Előzmény: [1505] Sirpi, 2006-11-14 11:40:26 |
|
|
| [1504] jenei.attila | 2006-11-14 11:32:30 |
 Kedves Cckek!
Először is maradjunk annyiban, tényleg érdekes a feladatot, csak kicsit másra számítottam. Másrészt nem egészen értem, mit is nem ismertünk fel? Azt, hogy Riemann-Stieltjes integrál közelítő összeg, észrevettük. Nadorp pedig megoldotta az integrálást, vagyis a feladat ezzel megoldódott.
|
| Előzmény: [1498] Cckek, 2006-11-13 18:16:57 |
|
|
|
|
| [1500] Cckek | 2006-11-13 18:37:41 |
 Amúgy a feladat főleg középiskolásoknak szól, itt csak azárt tűztem ki, mert már megjelent egy Erdély-i matematikai folyóiratban a MATLAP-ban, és nagyon kevés helyes megoldás érkezett:))
|
| Előzmény: [1499] Cckek, 2006-11-13 18:25:05 |
|
| [1499] Cckek | 2006-11-13 18:25:05 |
 Ami mellesleg egy jólismert cseles integrál :) az 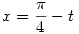 helyetesítéssel kiszámítható, és kitűnő példa olyan függvény integráljának a kiszámítására amelyenk nem ismerjük a primitív függvényét:)) helyetesítéssel kiszámítható, és kitűnő példa olyan függvény integráljának a kiszámítására amelyenk nem ismerjük a primitív függvényét:))
|
| Előzmény: [1498] Cckek, 2006-11-13 18:16:57 |
|
| [1498] Cckek | 2006-11-13 18:16:57 |
 Nos a feladat két okból is nagyon érdekes:)) Először mert az én szerzeményem:)), másodszor mert senki sem ismerte fel még - és ezt komolyan mondom-a nagyrabecsült jelenlévők közül sem hogy ez valójában egy Riemann összeg, mégpedig az
![f:[0,\frac{\pi}{4}]\to R, f(x)=ln(1+tgx)](keplet.cgi?k=E93A7EC15B68CCE4)
függvény es a
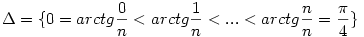 felosztáshoz rendelt Riemann integrálösszeg.Tehát egyenlő a felosztáshoz rendelt Riemann integrálösszeg.Tehát egyenlő a 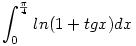 integrállal. integrállal.
|
| Előzmény: [1496] jenei.attila, 2006-11-13 13:54:16 |
|
|
| [1496] jenei.attila | 2006-11-13 13:54:16 |
 Szép megoldás, de most már kíváncsi lennék, Cckek szerint mitől is olyan érdekes ez a feladat. Nekem inkább kissé mesterkéltnek és "strapásnak" tűnik, hacsak nincs rá egy ettől különböző igazán szellemes megoldás.
|
| Előzmény: [1495] nadorp, 2006-11-13 13:31:54 |
|
|
|
|
|
|





