| [1540] Cckek | 2006-11-25 23:02:45 |
 Oldjuk meg az egész számok halmazán a következő egyenletet: 2m-1=xn
|
|
| [1539] jenei.attila | 2006-11-23 20:55:29 |
 Valóban, ez esetben a hányados tényleg 2, azonban a lényegen mit sem változtat. Egyébként ez az eset is benne van az előző hozzászólásomban, l=0-val. Az ez előtti megjegyzésem szerint, minden páratlan számra igaz, hogy a  (n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz. (n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz.
|
| Előzmény: [1538] S.Ákos, 2006-11-23 20:09:58 |
|
|
|
| [1536] jenei.attila | 2006-11-23 12:01:16 |
 Sőt. A páratlan számokhoz relatív prímek száma páros, vagyis nem lehet osztója a páratlan számnak. A páratlan számok reciprok összege pedig divergál. Szerintem kérdezzük meg Ákost, pontosam mire gondolt. Ákos! A kérdés adott: légyszíves pontosítsd a feladatot. Köszi.
|
| Előzmény: [1535] jenei.attila, 2006-11-23 11:24:47 |
|
| [1535] jenei.attila | 2006-11-23 11:24:47 |
 Én sem egészen értem a feladatot, de ha azon számok reciprok összegéről van szó, amelyeknek a náluk kisebb relatív prímek száma nem osztója, akkor a páratlan prímekre ez biztos igaz. Ezek reciprok összege, pedig valóban divergens, és következik belőle, hogy a szóban forgó számok reciprok összege is divergens. A prímekre vonatkozóan a bizonyítás nem túl könnyű, és lehet, hogy az Ákos által megfogalmazott gyengébb állítás bizonyítása könnyebb. Szerintem ez lehet a feladat.
|
| Előzmény: [1534] Lóczi Lajos, 2006-11-23 10:15:36 |
|
|
|
|
| [1531] Sirpi | 2006-11-22 22:53:47 |
 Lehet hogy rosszul gondolom, de én az állítást úgy értelmeztem, hogy azon egészek reciprokösszege, melyekre teljesül, hogy nem osztja őket a nála kisebb relatív prímek száma, végtelen.
|
| Előzmény: [1529] Lóczi Lajos, 2006-11-22 22:26:15 |
|
|
| [1529] Lóczi Lajos | 2006-11-22 22:26:15 |
 Csak 4 dolgot nem értek:
1. mi a különbség hi és Hi között
2. mit jelöl a  függvény függvény
3. mit jelöl a kapcsoszárójel
4. mire vonatkozik a limesz, ugyanis a szummában nincs már szabad változó
(Jobban érteném hi jelentését, ha látnám az első pár tagját.)
|
| Előzmény: [1528] S.Ákos, 2006-11-22 20:00:39 |
|
|
|
|
|
|
|
|
| [1521] Lóczi Lajos | 2006-11-19 17:44:40 |
 Oldjuk meg a valós számok halmazán a
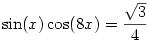
trigonometrikus egyenletet.
|
|
| [1520] Cckek | 2006-11-18 11:59:12 |
 Még valami. Az vajon eldönthető-e, hogy egy k inverzióval rendelkező n-edrendű permutáció hányféle képpen bontható fel transzpozíciók szorzatára? Én ezzel probálkoztam, persze nem jutottam sehova.:)
|
|
| [1519] Cckek | 2006-11-18 11:51:16 |
 Nagyon érdekes okfejtés. Az nyílvánvaló, már csak az inverziók számolási módszeréből is, hogy a t1+t2+...+tn-1=k összeg összes lehetséges képzésének a száma adja meg az n-edrendű k inverzióval rendelkező permutációk számát, hiszen ha a permutáció alsó sorában 1 előtt t1, 1-nél nagyobb, 2 előtt t2, 2-nél nagyobb,.. (n-1) előtt tn-1, (n-1)-nél nagyobb elem van akkor a permutáció inverzióinak a száma t1+t2+...+tn-1. Az is látható, hogy 0 t1 t1 (n-1), 0 (n-1), 0 t2 t2 (n-2),...,0 (n-2),...,0 tn-1 tn-1 1 Tehát, a problémát, kitűnően letárgyáltátok, itt valóban nem beszélhetünk zárt alakról, annyit még hozzátennék, hogy amennyiben Skn-el jelöljük a k inverzióval rendelkező n-edrendű permutációk számát úgy fennáll : 1 Tehát, a problémát, kitűnően letárgyáltátok, itt valóban nem beszélhetünk zárt alakról, annyit még hozzátennék, hogy amennyiben Skn-el jelöljük a k inverzióval rendelkező n-edrendű permutációk számát úgy fennáll :
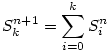
Attila is említett egy rekurziót. Az hogy néz ki?
|
| Előzmény: [1518] nadorp, 2006-11-18 10:22:10 |
|
| [1518] nadorp | 2006-11-18 10:22:10 |
 Megpróbálom vázolni a gondolatmenetemet. Jelölje az n-edrendű k inverziót tartalmazó permutációk számát I(n,k) és legyen p(n,k) egy ilyen permutáció. Ekkor ha az n+1 elemet a permutáció végére tesszük, akkor egy p(n+1,k) permutációt kapunk. Ha az n+1-et eggyel balra tolva a n-dik helyre tesszük, akkor egy p(n+1,k+1) permutációt kapunk stb. ha az n+1 az első helyen van, akkor egy p(n+1,k+n) permutációt kapunk. Foglaljuk be ezt az alábbi táblázatba, ahol a k-dik oszlopban a p(n,k)-ból kapható permutációk találhatóak.
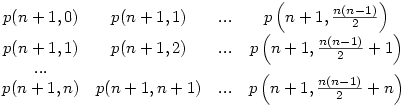
Tekintsük még a következő hasonló táblázatot
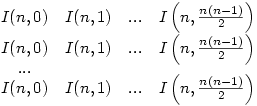
Nyilvánvaló, hogy I(n+1,k) úgy kapható meg, hogy ahol az első táblázatban p(n+1,k) van, összeadjuk a második táblázatban az ezeken a helyeken szerplő I(n,...) értékeket.Tehát
I(n+1,0)=I(n,0)
I(n+1,1)=I(n,0)+I(n,1)
I(n+1,2)=I(n,0)+I(n,1)+I(n,2) stb..
Ezek az összegek éppen balról jobbra haladva a "balról jobbra fel átlókon" levő elemek összege. Ha most fn(x) az I(n,k) sorozat (n fix) generátor függvénye, azaz
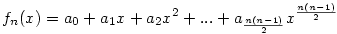 , ahol ak=I(n,k), akkor , ahol ak=I(n,k), akkor
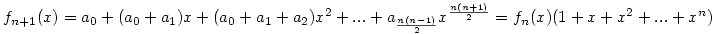
|
| Előzmény: [1516] jenei.attila, 2006-11-16 15:44:31 |
|
| [1517] jenei.attila | 2006-11-16 15:50:44 |
 Egyébként (mint azóta utána néztem), D.E. Knuth: A számítógépes programozás művészete c. könyv harmadik kötete (Rendezések és keresések) is részletesen foglalkozik a problémával. Ott egy érdekes rekurziót is megad. A könyvet nagyon ajánlom mindenkinek.
|
| Előzmény: [1516] jenei.attila, 2006-11-16 15:44:31 |
|
|




 (n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz.
(n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz.


 t1
t1