|
|
| [1551] Hajba Károly | 2006-11-29 00:49:24 |
 Rendezzük az egyenletet:
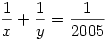
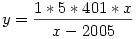
Ahhoz, hogy y egész lehessen, a nevező értékének a számláló valamely részszorzatával kell egyenlőségben lennie. Ez 7 megoldást ad, melyből 3-3 'szimmetrikus'.

|
| Előzmény: [1550] Csimby, 2006-11-28 23:01:50 |
|
| [1550] Csimby | 2006-11-28 23:01:50 |
 241.feladat
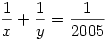
Keressük a pozitív egész megoldásokat. (Lehet, hogy már volt, ez esetben sorry)
|
|
|
| [1548] Cckek | 2006-11-26 15:40:18 |
 Most már egyszerű bebizonyítani azt is,hogy ha: 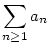 konvergens akkor konvergens akkor
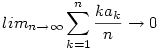 . .
Gondolkozzunk a következő határértéken:

|
|
|
|
|
| [1544] ScarMan | 2006-11-26 13:41:17 |
 Szerintem ebben az esetben a határérték csak 0 lehet.
Ha an-nek végtelen sok pozitív és negatív tagja van, akkor ez nan-re is igaz, de ekkor a két részsorozat közös határértéke csak a 0 lehet.
Ha valamelyik előjelű tagból csak véges sok van, akkor azokat hagyjuk el. Ha most csak negatív tagjaink maradtak, akkor szorozzuk az egészet -1-gyel. Most csak pozitív tagjanik vannak. Itt találunk egy szig. mon. csökkenően 0-hoz tartó részsorozatot, ez legyen aN. Nyilván 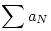 is konvergens, mert pozitív tagokat hagytunk el. Ekkor a Cauchy-féle ekvikonvergencia tétel miatt is konvergens, mert pozitív tagokat hagytunk el. Ekkor a Cauchy-féle ekvikonvergencia tétel miatt 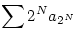 sor is konvergens, ezért az általános tag 0-hoz tart. Ez NaN-nek részsorozata, ami viszont nan-nek részsorozata, tehát nan-nek 0 torlódási pontja. sor is konvergens, ezért az általános tag 0-hoz tart. Ez NaN-nek részsorozata, ami viszont nan-nek részsorozata, tehát nan-nek 0 torlódási pontja.
|
| Előzmény: [1543] Cckek, 2006-11-26 12:12:20 |
|
|
|
| [1541] Cckek | 2006-11-26 11:52:55 |
 Adjunk páldát olyan an sorozatra, melyre 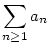 konvergens, de nan határértéke nem 0. konvergens, de nan határértéke nem 0.
|
|
| [1540] Cckek | 2006-11-25 23:02:45 |
 Oldjuk meg az egész számok halmazán a következő egyenletet: 2m-1=xn
|
|
| [1539] jenei.attila | 2006-11-23 20:55:29 |
 Valóban, ez esetben a hányados tényleg 2, azonban a lényegen mit sem változtat. Egyébként ez az eset is benne van az előző hozzászólásomban, l=0-val. Az ez előtti megjegyzésem szerint, minden páratlan számra igaz, hogy a  (n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz. (n) nem osztója n-nek, vagyis elég csak a páratlan számok reciprok összegéről belátni, hogy divergens. Ez pedig közismert. A legutóbbi megjegyzésem már egy erősebb állítást tartalmaz.
|
| Előzmény: [1538] S.Ákos, 2006-11-23 20:09:58 |
|
|
|
| [1536] jenei.attila | 2006-11-23 12:01:16 |
 Sőt. A páratlan számokhoz relatív prímek száma páros, vagyis nem lehet osztója a páratlan számnak. A páratlan számok reciprok összege pedig divergál. Szerintem kérdezzük meg Ákost, pontosam mire gondolt. Ákos! A kérdés adott: légyszíves pontosítsd a feladatot. Köszi.
|
| Előzmény: [1535] jenei.attila, 2006-11-23 11:24:47 |
|
| [1535] jenei.attila | 2006-11-23 11:24:47 |
 Én sem egészen értem a feladatot, de ha azon számok reciprok összegéről van szó, amelyeknek a náluk kisebb relatív prímek száma nem osztója, akkor a páratlan prímekre ez biztos igaz. Ezek reciprok összege, pedig valóban divergens, és következik belőle, hogy a szóban forgó számok reciprok összege is divergens. A prímekre vonatkozóan a bizonyítás nem túl könnyű, és lehet, hogy az Ákos által megfogalmazott gyengébb állítás bizonyítása könnyebb. Szerintem ez lehet a feladat.
|
| Előzmény: [1534] Lóczi Lajos, 2006-11-23 10:15:36 |
|
|
|
|
| [1531] Sirpi | 2006-11-22 22:53:47 |
 Lehet hogy rosszul gondolom, de én az állítást úgy értelmeztem, hogy azon egészek reciprokösszege, melyekre teljesül, hogy nem osztja őket a nála kisebb relatív prímek száma, végtelen.
|
| Előzmény: [1529] Lóczi Lajos, 2006-11-22 22:26:15 |
|
|
| [1529] Lóczi Lajos | 2006-11-22 22:26:15 |
 Csak 4 dolgot nem értek:
1. mi a különbség hi és Hi között
2. mit jelöl a  függvény függvény
3. mit jelöl a kapcsoszárójel
4. mire vonatkozik a limesz, ugyanis a szummában nincs már szabad változó
(Jobban érteném hi jelentését, ha látnám az első pár tagját.)
|
| Előzmény: [1528] S.Ákos, 2006-11-22 20:00:39 |
|




 =
= =0
=0  1
1  multiplikativitását
multiplikativitását 






