|
| [1563] rizsesz | 2006-11-30 17:53:35 |
 pontosan 10. ugye egy lámpát pontosan annyiszor vált át, ahány osztója van. két érdekes állapot van, a lekapcsolt, illetve a felkapcsolt villany. a felkapcsolthoz páratlan sok, a másikhoz páros sok váltás kell. így azok maradnak égve, amelyeknek páratlan sok osztója van, ezek a négyzetszámok, amelyekből 10 darab van (1, 4, 9...100).
|
|
| [1562] nervus | 2006-11-30 17:10:55 |
 Jah, maga a kérdés az az, hogy a végére hány lámpa marad égve? Előre is köszi:)
|
|
| [1561] nervus | 2006-11-30 16:56:31 |
 Üdv! Tudnátok segíteni 1 feladatban? Már órák óta gondolkozom rajta, de nem jöttem rá :( Egy üres, 100 szobás szállodában unatkozik a portás:) Elindul, és felkapcsol minden villanyt. Aztán visszafordul, és lekapcsol minden 2. lámpát. Majd újra elindul (3. kör) és minden 3. lámpát átvált (ha le van kapcsolva, felkapcsolja, ha fel, lekapcsolja). Ahanyadik kört teszi meg (vagyis csak 100 lehet), annyiadik szobának a lámpáját változtatja meg. (10 kör, minden 10. lámpa.. stb) Aki tudja, help légyszi:S
|
|
| [1560] jenei.attila | 2006-11-30 14:56:23 |
 Közben látom te is megelőztél a feltöltéssel, én is az ábrádhoz hasonló háromdxögre gondoltam. Csak nem vetted figyelembe a másik esetet, amikor x>y. Én kitartok az 1/4 mellett.
|
| Előzmény: [1568] Ali, 2006-11-30 14:53:10 |
|
| [1559] jenei.attila | 2006-11-30 14:53:57 |
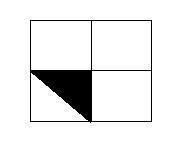
 Látom közben neked is ez jött ki, ez biztató. Egyébként én az x,y síkbeli koordináta rendszer (0,0), (1,0), (1,1), (0,1) egységnégyzetében veszek fel egy pontot (egyenletes eloszlás szerinti valószínűséggel), amelynek x ill. y koordinátája megadja a [0,1] intervallum egy felosztását. Az x, y-x, 1-y (ha x<=y) szakaszokból pontosan akkor szerkeszthető háromszög, ha mindegyik hossza 1/2-nél kissebb. A koordinátarendszerben ábrázolva azt jelenti, hogy a kivélasztott pont az x=1/2, y=1/2, y=x+1/2 egyenesek által határolt háromszögbe esik. Ennek területe 1/8. Amikor x>y, hasonlóan egy 1/8 területű háromszög lesz a megfelelő tartomány. Tehát a keresett valószínűség 1/4.
|
| Előzmény: [1557] Sirpi, 2006-11-30 14:27:02 |
|
|
|
|
|
|
| [1554] lorantfy | 2006-11-30 10:35:07 |
 300. feladat. Egységnyi szakaszt véletlenszerűen 3 részre vágunk szét. Mekkora a valószinüsége, hogy a három részből háromszög szerkeszhető? (TK. példa)
|
|
|
|
| [1551] Hajba Károly | 2006-11-29 00:49:24 |
 Rendezzük az egyenletet:
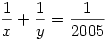
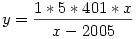
Ahhoz, hogy y egész lehessen, a nevező értékének a számláló valamely részszorzatával kell egyenlőségben lennie. Ez 7 megoldást ad, melyből 3-3 'szimmetrikus'.

|
| Előzmény: [1550] Csimby, 2006-11-28 23:01:50 |
|
| [1550] Csimby | 2006-11-28 23:01:50 |
 241.feladat
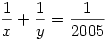
Keressük a pozitív egész megoldásokat. (Lehet, hogy már volt, ez esetben sorry)
|
|
|
| [1548] Cckek | 2006-11-26 15:40:18 |
 Most már egyszerű bebizonyítani azt is,hogy ha: 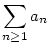 konvergens akkor konvergens akkor
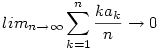 . .
Gondolkozzunk a következő határértéken:

|
|
|
|
|
| [1544] ScarMan | 2006-11-26 13:41:17 |
 Szerintem ebben az esetben a határérték csak 0 lehet.
Ha an-nek végtelen sok pozitív és negatív tagja van, akkor ez nan-re is igaz, de ekkor a két részsorozat közös határértéke csak a 0 lehet.
Ha valamelyik előjelű tagból csak véges sok van, akkor azokat hagyjuk el. Ha most csak negatív tagjaink maradtak, akkor szorozzuk az egészet -1-gyel. Most csak pozitív tagjanik vannak. Itt találunk egy szig. mon. csökkenően 0-hoz tartó részsorozatot, ez legyen aN. Nyilván 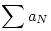 is konvergens, mert pozitív tagokat hagytunk el. Ekkor a Cauchy-féle ekvikonvergencia tétel miatt is konvergens, mert pozitív tagokat hagytunk el. Ekkor a Cauchy-féle ekvikonvergencia tétel miatt 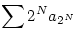 sor is konvergens, ezért az általános tag 0-hoz tart. Ez NaN-nek részsorozata, ami viszont nan-nek részsorozata, tehát nan-nek 0 torlódási pontja. sor is konvergens, ezért az általános tag 0-hoz tart. Ez NaN-nek részsorozata, ami viszont nan-nek részsorozata, tehát nan-nek 0 torlódási pontja.
|
| Előzmény: [1543] Cckek, 2006-11-26 12:12:20 |
|
|
|
| [1541] Cckek | 2006-11-26 11:52:55 |
 Adjunk páldát olyan an sorozatra, melyre 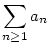 konvergens, de nan határértéke nem 0. konvergens, de nan határértéke nem 0.
|
|






 =
= =0
=0  1
1  multiplikativitását
multiplikativitását 




