|
| [1666] Python | 2007-01-01 15:29:09 |
 304. feladat
a)Végződhet-e egy kettőhatvány 3 egyforma számjegyre? (10-es számrendszer)
b)Végződhet-e egy kettőhatvány 4 egyforma számjegyre? (10-es számrendszer)
|
|
| [1665] Lóczi Lajos | 2006-12-31 14:00:09 |
 Számunkra már több, mint egy éve nyitott az alábbi ártatlannak tűnő kérdés: oldjuk meg a valós számok halmazán a
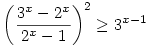
egyenlőtlenséget. Az eredményt persze tudjuk, csak a bizonyítást nem. Hátha valaki talál egy ügyes utat...
|
|
|
|
| [1662] Cckek | 2006-12-30 17:53:39 |
 Jólismert egyenlőtlenségek a G<L<A ahol
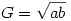 , ,
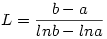 , ,
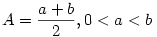 . .
Tud rájuk valaki egy egyszerű bizonyítást?
|
|
| [1661] HoA | 2006-12-29 16:40:53 |
 A képlet bizonyítása: Rakjunk le egy sorba s + n - 1 ( 222 + 4 - 1 = 225 ) fehér korongot. Közülük n-1 (3) tetszőlegeset takarjunk le egy-egy fekete koronggal. Minden ilyen lefedés a le nem takart s (222) korongot n (4) csoportra bontja, melyek közt 0 elemszámúak is lehetnek. Feleltessük meg, mondjuk balról jobbra az egyes csoportok elemszámát az ai (x,y,z,t) változóknak, ekkor egyenletünk egy megoldását kapjuk. Így kölcsönösen egyértelmű leképezést kapunk a lefedések és a megoldások között, tehát megoldás is ponosan annyi van, mint lefedés. Ezek száma pedig a képlet szerinti.
|
| Előzmény: [1660] Cckek, 2006-12-29 10:33:28 |
|
|
|
|
| [1657] Cckek | 2006-12-28 15:06:49 |
 Hány megoldása van a természetes számok halmazában az x+y+z+t=222 egyenletnek?
|
|
| [1656] HoA | 2006-12-27 13:24:26 |
 Mivel eddig senki sem szólt hozzá, leírok egy megoldást.
Racionáls a,b 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 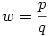 , , 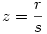 , ahol p,q,r,s egészek. , ahol p,q,r,s egészek. 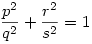 ; p2s2+r2q2=q2s2 Legyen q és s legnagyobb közös osztója n, q=tn, s=un, ahol t és u relatív prímek. ; p2s2+r2q2=q2s2 Legyen q és s legnagyobb közös osztója n, q=tn, s=un, ahol t és u relatív prímek.
p2u2n2+r2t2n2=t2u2n4 ; p2u2+r2t2=t2u2n2 A baloldalon t és u relatív prím volta miatt p2 osztható t2 -tel és r2 osztható u2 -tel. Legyen p=kt, r=mu. k2t2u2+m2u2t2=t2u2n2
k2+m2=n2
Vagyis tetszőleges k,m,n pithagoraszi számhármashoz kapunk megoldást. Visszafelé haladva tetszőleges relatív prím t-t és u-t véve 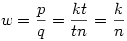 , , 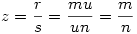 , , 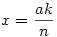 , , 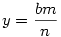
Az ellipszis racionális koordinátájú pontjai tehát a 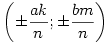 pontnégyesek, ahol a és b az ellipszis tengelyei, k,m,n pithagoraszi egészek, ahol a nemnulla hármasokon kívül 1;0;1 és 0;1;1 is megengedett. Könnyen belátható, hogy ha k,m,n primitív pithagoraszi számhármas, akkor minden pontot csak egyszer kapunk meg. pontnégyesek, ahol a és b az ellipszis tengelyei, k,m,n pithagoraszi egészek, ahol a nemnulla hármasokon kívül 1;0;1 és 0;1;1 is megengedett. Könnyen belátható, hogy ha k,m,n primitív pithagoraszi számhármas, akkor minden pontot csak egyszer kapunk meg.
|
| Előzmény: [1625] Cckek, 2006-12-15 14:58:40 |
|
|
|
| [1653] Hephon | 2006-12-25 16:17:19 |
 Minden üveg sorszáma elfér 10 számjegyen binárisan (<1024). Minden bináris helyiérték 1-1 halálraitélthez tartozik. Minden borral megitatja azokat az embereket, ahol ez a helyiérték 1, tehát az 1. borbol csak az első szolga, a 100. borbol(64+32+4) tehát a 3. 5. 6. halálraitéltek isznak. 30. nap után az összes halottbol kiszámítha, hogy melyik bor volt a mérgező.
|
| Előzmény: [1652] Cckek, 2006-12-25 15:55:58 |
|
| [1652] Cckek | 2006-12-25 15:55:58 |
 Kellemes ünnepeket mindenkinek. És... a következő kis feladatot: Egy császár 1000 üveg borából 1 mérgezett. A császár kiadja a nagyvezérnek a parancsot, 40 nap alatt állapítsa meg melyik üveg mérgezett. Ehez kap 10 halálraítéltet akikkel a borokat kostoltathatja. A méreg 30 nap mulva hat. Hogyan jár el a nagyvezér?
|
|
|
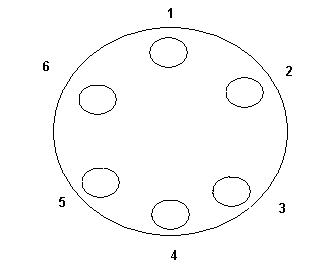
| [1650] Iván88 | 2006-12-21 20:34:16 |
 Mivel a rendszer nem engedi feltölteni a 343 bájtos ábrámat (ami jóval a maximum alatt van) a kitöltetlen ábrádon fogok magyarázni. 4 különböző eset van a kézbedugásra:
3 szomszédos állásba (612)
2 szomszédos állásba, (124 ill. 614-ezek forgatással nyilván nem vihetők át egymásba)
0 szomszédos állásba (246)
Az össze további eset ezek közül valamelyiknek az elforgatottja.
A kapcsolók állása nyilván csak goldolatban van megszámozva, különben nem feladat. Ezzel a 4 félével, ha nincs szerencsénk, akkor kijöhet, hogy csak az 1246 kapcsolókhoz nyúlunk hozzá.
Tehát, ha a 3-as, és az 5-ös kapcsoló különböző állású, akkor elvileg az is előfordulhat, hogy sose nyúlunk hozzájun, és az ajtó is zárva maradhat az idők végezetéig.
Tehát áltaéános algoritmus nem létezik.
|
| Előzmény: [1649] magusocska, 2006-12-21 19:00:59 |
|
| [1649] magusocska | 2006-12-21 19:00:59 |
 Eddig jutottam:
Jelöljük a kapcsoló két állását 1-gyel és 2-vel!
Jelöljük a kapcsolókat 1-6, a felsőtől az óramutató járásával megegyezően.
[Ekkor az első kapcsoló jelölése legyen 1(1) vagy 1(2) attól függően, hogyan áll a kapcsoló 1 vagy 2 állásban, bizonytalan helyzetben 1 (1/2).]
Minden továbblépés előtt feltételezzük, hogy nem nyílik ki.
[Szerencsés esetben persze bármikor kinyílhat, akár induláskor is :*-) ]
1. Fogjunk meg három egymás melletti kapcsolót, és állítsuk mindhármat 2-re, ha nem az volt! [1(2),2(2),3(2) kapcsolóállás jön létre]
2.A pörgetés után fogjunk meg három nem egymás mellettit, és állítsuk 2-re, ha nem az volt!
A lehetséges esetek:
hely----Biztos--------------------bizonytalan
1,3,5--1(2),2(2),3(2),5(2)--------4(1/2),6(1/2)
2,4,6--1(2),2(2),3(2),4(2),6(2)---5(1/2)
Tehát két pörgetés után mindkét esetben legalább egy bizonytalan helyem van. Innentől én is bizonytalan vagyok.
Mivel a pörgetés véletlenszerű kezdőpontú felállásokat hoz, elvben bármeddig pörgethetek, nézhetem, hogy van-e átállítandó (ha 1 akkor átállítom), de mi garantálja, hogy a három kezem közül valamelyik alá kerül a hátralévő (1 vagy 2) a maradék 3 pörgés alatt?
Nem látom értelmét annak sem, hogy az 1,2,3 és a 2,4,6 után egy újabb lépésvariációt vezessek be (mondjuk 1,2,4).
Ötlet?
|
 |
| Előzmény: [1647] magusocska, 2006-12-21 10:52:17 |
|
|
| [1647] magusocska | 2006-12-21 10:52:17 |
 Csernobili probléma néven a 81.-eshez hasonlót adtak fel a lányomnak az iskolába, de 6 lyuk és 3 kéz (sic!) esetén. Ez lehet 81/a vagy valami újabb, de a lényeg, hogy van-e ötletetekt ötlépéses megoldásra, vagy annak cáfolatára.
|
|
|
| [1645] JBence | 2006-12-20 22:24:24 |
 Van egy jó kis feladatom, lehet hogy a logikához kellett volna írni de mindegy: Van egy kétkarú mérlegünk és 12 golyónk. A golyók közül egynek más a tömege mint a másik tizenegyé, de nem tudjuk hogy nehezebb vagy könnyebb. Állapítsuk meg 3 mérésből hogy melyik a rossz golyó és hogy könnyebb e vagy nehezebb. Sok sikert :)
|
|
|
|








 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen
0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 





