| [1693] Lóczi Lajos | 2007-01-07 02:55:59 |
 Nyilván azzal kell kezdeni a bizonyítást, hogy a b sorozat bemegy a [-3 ,3 ,3 ] intervallumba. ] intervallumba.
"Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2-nál nagyobb értékhez nem tud konvergálni." felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2-nál nagyobb értékhez nem tud konvergálni."
De ha nem menne be, miért maradna 3 felett? Miért ne ugrálhatna (pozitív és negatív értékekre) és főleg, miért kellene, hogy monoton legyen a b sorozat? felett? Miért ne ugrálhatna (pozitív és negatív értékekre) és főleg, miért kellene, hogy monoton legyen a b sorozat?
|
| Előzmény: [1688] Sirpi, 2007-01-04 23:47:54 |
|
|
| [1691] nadorp | 2007-01-06 12:56:32 |
 Legyen bn=an+2an+1. Ekkor
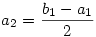
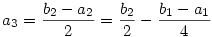
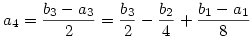
...
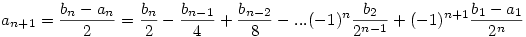 . .
Mivel 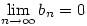 , ezért n>N esetén |bn|< , ezért n>N esetén |bn|< , azaz , azaz
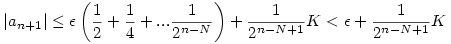 , ahol K a |b1-a1|,|b2|,|b3|... egy közös felső korlátja. ( Ez létezik, mert bn konvergens). Innen már látszik, hogy , ahol K a |b1-a1|,|b2|,|b3|... egy közös felső korlátja. ( Ez létezik, mert bn konvergens). Innen már látszik, hogy 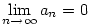
|
| Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16 |
|
|
|
| [1688] Sirpi | 2007-01-04 23:47:54 |
 Igaznak tűnik :-)
Tegyük fel, hogy an nem azonosan 0 egy adott indextől kezdve, és teljesül rá a feltétel. Cseréljük ki an-et egy bn sorozatra úgy, hogy bn=an, ha n páros, és bn=-an, ha n páratlan. Ekkor a feltétel ekvivalens bn/2-bn+1 konvergenciájával (ezzel egyszerűbb talán dolgozni, mert nem "oszcillál").
Legyen  >0. Ekkor a konvergencia miatt van olyan N, hogy minden n>N-re |bn/2-bn+1|< >0. Ekkor a konvergencia miatt van olyan N, hogy minden n>N-re |bn/2-bn+1|< . .
Mivel bn nem azonosan nulla valamilyen indextől, ezért van olyan m>N, amire bm 0 (feltehetjük, hogy pozitív, különben a bn sorozat helyett vegyük az ellentettjét). Ekkor bm/2- 0 (feltehetjük, hogy pozitív, különben a bn sorozat helyett vegyük az ellentettjét). Ekkor bm/2-  bm+1 bm+1 bm/2+ bm/2+ , vagyis (és ez a lényeg) a sorozot bm-től kezdve előbb-utóbb bemegy a [-3 , vagyis (és ez a lényeg) a sorozot bm-től kezdve előbb-utóbb bemegy a [-3 ;3 ;3 ] intervallumba, és onnan már nem is tud kijönni, így 3 ] intervallumba, és onnan már nem is tud kijönni, így 3 -hoz van megfelelő N' korlát. -hoz van megfelelő N' korlát.
Az, hogy ha bemegy, akkor nem tud kijönni, triviális, hiszen 0/2-  bn+1 bn+1 3/2 3/2 + + , azaz a következő elem abszolútértéke 5/2 , azaz a következő elem abszolútértéke 5/2 lesz maximum. Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 lesz maximum. Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2 -nál nagyobb értékhez nem tud konvergálni. -nál nagyobb értékhez nem tud konvergálni.
Tudom, ez így kicsit kusza, meg hosszú volt, de már kezd késő lenni. Nem tudom, van-e sokkal egyszerűbb(en leírható) megoldás.
|
| Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16 |
|
| [1687] Lóczi Lajos | 2007-01-04 22:25:16 |
 Bizonyítsuk be vagy cáfoljuk meg az alábbi állítást:
"Ha an egy olyan korlátos valós számsorozat, amelyre an+2an+1 nullához tart, akkor an konvergens" (és ekkor persze maga is nullsorozat).
|
|
|
|
|
|
|
|
|
|
|
|
| [1675] Mumin | 2007-01-01 20:10:32 |
 Hány SET-kártyát lehet legfeljebb kirakni az asztalra, hogy ne kiálthasson senki Set!-et?
Aki egyszerűnek találja, ne lője le.
|
|
|
| [1673] S.Ákos | 2007-01-01 19:11:48 |
 Maradékvizsgálat nélkül: Mivel a 0001;0002;0004;0008;0016 végződések nem felelnek meg, így az utolsó négy számjegyből alkotott szám osztható 16-tal és 1111-gyel, de ezeknek a közös többszörösei 0;17776;... így csak a 0000 jöhet szóba, de ez lehetetlen.
|
| Előzmény: [1671] jonas, 2007-01-01 17:32:26 |
|
|
| [1671] jonas | 2007-01-01 17:32:26 |
 (a) 239=549755813888
(b) Ehhez elég a 2-hatványok 10000-es maradékát megvizsgálni. Ez persze ciklikus, hiszen 2504 24 24 16mod 10000. A maradékok 2503-ig sorban könnyen kiszámolhatóak (nem másolom ide az összeset): 16mod 10000. A maradékok 2503-ig sorban könnyen kiszámolhatóak (nem másolom ide az összeset):
0001 0002 0004 0008 0016 0032 0064 0128 0256 0512 1024 2048 4096 8192 6384 2768 5536 1072 2144 4288 8576 7152 4304 8608 7216 4432 8864 7728 ... 8752 7504 5008
Ezek között pedig nincs 1111-gyel osztható.
|
| Előzmény: [1666] Python, 2007-01-01 15:29:09 |
|
|
| [1669] Lóczi Lajos | 2007-01-01 17:21:13 |
 a.) Az első 1600 kitevő átvizsgálása az alábbi eredményt adja: 2n pontosan akkor végződik 3 egyforma számjegyre, ha n az alábbi:
n=39,139,239,339,439,.... Ekkor amúgy mindig 888-ra végződik 2n.
b.) A számítógép 85 másodperc gondolkodás után nem tudott olyan 2-hatványt mondani, ami 4 egyforma számjegyre végződne. Az átvizsgált n kitevők tartománya: n=1-től egészen n=107-ig.
|
| Előzmény: [1666] Python, 2007-01-01 15:29:09 |
|
|



 ,3
,3
 , azaz
, azaz 
 0, ahol m>N, ahol N az
0, ahol m>N, ahol N az  0 és így an
0 és így an bm+1
bm+1
 36-tól működik (a 36 valójában csak az egyik irányú egyenlőtlenséghez kell, a másik n
36-tól működik (a 36 valójában csak az egyik irányú egyenlőtlenséghez kell, a másik n



 24
24