| [1706] psbalint | 2007-01-09 15:38:27 |
 Üdvözlök mindenkit! Egy feladatot szeretnék elmondani, remélem még nem volt, ha volt, elnézést. Nagyon egyszerűnek tűnik mégsem boldogulok vele...
Egy kör alakú kert sugara r, a körvonal egy pontjához belülről hozzákötünk egy kecskét egy kötéllel. Milyen hosszú legyen a kötél, hogy a kecske a kör területének felét tudja lelegelni?
|
|
|
|
| [1703] Cckek | 2007-01-08 22:22:19 |
 Ugyan már máshol is kitűztem, de nem érkezett megoldás rá, remélem itt együttesen megoldjuk: Oldjuk meg a következő funkcionálegyenletet
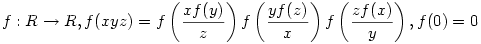 . .
|
|
| [1702] magusocska | 2007-01-08 19:33:53 |
 Egy QBASIC program 2.5 mp alatt kihozta, hogy 48 megoldás van.
A progi lényegében kipróbálta az oszhatósági szabályokat a fokozatosan növelt helyiértékszámú számokra.
Más, "elegánsabb" módszer nem lenne?
|
| Előzmény: [1697] magusocska, 2007-01-08 08:03:44 |
|
| [1701] bgy67 | 2007-01-08 17:49:27 |
 A következő problémám lenne, segítsen, aki tud!
12k+4 embert akarok 4-személyes asztalokhoz leültetni (römi-verseny) 4k+1 fordulóban úgy, hogy mindenki mindenkivel pontosan egyszer játsszon.
Egy órát kerestem google-val, de nem találtam táblázatot, csak azt a tételt, hogy ez mindig megoldható.
16 személyre meg is csináltam, egyszerűen mindig a legkisebb lehetséges sorszámú személyt ültettem le sorban és kijött, lehet hogy ez mindig működne, de programozni annyira nem tudok, hogy megcsináljam, kézzel meg hosszú. "Szép" mintát meg nem találtam, amit általánosítani lehetne.
Aki találkozott a problémával (gráfelmélet, véges testek??), és tud sorsolást leglább 28 és 40 főre, pls szóljon.
|
|
| [1700] magusocska | 2007-01-08 09:52:47 |
 Teljesen igazad van - elnézést kérek [ vadidegenül szorri :-)) ]
Csak magyarázatképpen említem meg, hogy
- túlságosan hozzá vagyok (gyunk) szokva az intelligens ellenőrzőrendszerekhez (nincs aláhúzás? akkor mehet)
- egy sort írtam le, a többi másoltam, és csak a számokat javítottam át, a toldalékokat nem
- a gyors kommunikációs kényszer (sms, email,chat) miatt egyre kevesebb jelentőséget tulajdonítunk (és sajnos ezek szerint -tok) a helyesírási konvencióknak
- és Proszékyék még nem publikálták a KÖMAL fórumra is alkalmazható ellenőrző rutincsomagjukat :-)
|
| Előzmény: [1699] BohnerGéza, 2007-01-08 09:02:58 |
|
| [1699] BohnerGéza | 2007-01-08 09:02:58 |
 Nagyon örvendetes, ha valaki tisztában van idegen szavak jelentésével. ( politikai publicitás, korifeus, kontextus, konvenció )
De jó lett volna az alapvető magyar szabályokat is betartani az előző hozzászólásban! ( Teljes hasonulás. )
kilenccel 9-cel nyolccal 8-cal ...
a legcsúnyább a 2-el, a 2-vel helyett!
Sajnos rengeteg helyen látni rosszul írva ezeket a sajtóban!
|
| Előzmény: [1698] magusocska, 2007-01-08 08:20:32 |
|
| [1698] magusocska | 2007-01-08 08:20:32 |
 Érdekes is, matematika is, de kérdés, hogy feladat-e, mindenesetre túl vagyok rajta.
Peano politikai publicitásáról hallottatok-e? (Összerugtam a port a lányom matektanárjával - így derült ki az ellentmondás.)
A természetes számok Peano féle meghatározása tartalmazta a nullát, az én egyetemi jegyzeteimben a természetes számok pozitív egészként szerepeltek, ma ismét az eredeti halmaz a hivatalos. A Lomonoszov korifeusaival lehet kapcsolatban az ügylet...
Tehát a kérdés (feladat): a magyar matematikaoktatásban mely években tanították a természetes számok halmazát az eredeti Peano-axiómától eltérően?
Megjegyzés:
A Wikipédia a következőt írja a "Természetes számok"-nál :
Vigyázat! Tekintve, hogy egyes matematikai tárgyú könyvek a természetes számok közé sorolják a nullát, mások nem, így minden esetben figyelmet kell fordítanunk arra, hogy utánanézzünk, az adott kontextusban a szerzők melyik konvenciót alkalmazzák.
|
|
| [1697] magusocska | 2007-01-08 08:03:44 |
 Mellyek az a 9 jegyű számok, amire igazak az alábbiak:
a 9 jegyű szám osztható 9-el,
ha elhagyjuk az utolsó jegyét, akkor az így kapott 8 jegyű szám osztható 8-al,
ha elhagyjuk az utolsó jegyét, akkor az így kapott 7 jegyű szám osztható 7-el,
. . .
ha elhagyjuk az utolsó jegyét, akkor az így kapott 2 jegyű szám osztható 2-el.
Elég könnyű legalább egyet találni (pl. 13694729) a jegyenkénti szabályalkalmazással, de az összes megtalálására a brutal force-n kívül van -e módszer?
|
|
|
| [1695] Sirpi | 2007-01-07 07:11:10 |
 Igaz, hogy már elhangzott egy sokkal frappánsabb megoldás (grat érte), de azért ha már kérdés, válaszolok:
Mivel |bn/2-bn+1|< minden n>N-re a folytonosság miatt, ezért bn/2- minden n>N-re a folytonosság miatt, ezért bn/2-  bn+1 bn+1 bn/2+ bn/2+ . Vagyis ha bn . Vagyis ha bn 3 3 , akkor (3/2-1) , akkor (3/2-1)  bn+1, tehát nem válthat előjelet (a bal oldali egyenlőtlenséget felhasználva), másrészt bn+1 bn+1, tehát nem válthat előjelet (a bal oldali egyenlőtlenséget felhasználva), másrészt bn+1 bn/2+ bn/2+  bn/2+bn/3 bn/2+bn/3 bn, tehát a sorozat monoton is. bn, tehát a sorozat monoton is.
Azt hittem, hogy ezek teljesen nyilvánvalónak látszanak az egyenlőtlenségből, azért nem részleteztem a dolgot ennyire.
Ha bn<0, akkor ugyanez elmondható, csak akkor a sorozat alulról, szintén monoton módon megy be a [-3 ;3 ;3 ] intervallumba. ] intervallumba.
|
| Előzmény: [1693] Lóczi Lajos, 2007-01-07 02:55:59 |
|
| [1694] Lóczi Lajos | 2007-01-07 03:23:19 |
 Köszönöm a megoldásokat, az állítás igazsága viszont azt jelenti, hogy most van egy sokkal kevesebb számolást igénylő megoldásunk az [1681]-es hozzászólás feladatára, az ugyanis alig igényel számolást belátni, hogy
un=2n-4/3+an
alakú, ahol an+2an+1 nullához tart és korlátos, tehát most már valóban tudjuk, hogy maga an is nullához tart, ez pedig elég ahhoz, hogy a -19/12-et kihozzuk.
|
| Előzmény: [1692] nadorp, 2007-01-07 00:32:48 |
|
| [1693] Lóczi Lajos | 2007-01-07 02:55:59 |
 Nyilván azzal kell kezdeni a bizonyítást, hogy a b sorozat bemegy a [-3 ,3 ,3 ] intervallumba. ] intervallumba.
"Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2-nál nagyobb értékhez nem tud konvergálni." felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2-nál nagyobb értékhez nem tud konvergálni."
De ha nem menne be, miért maradna 3 felett? Miért ne ugrálhatna (pozitív és negatív értékekre) és főleg, miért kellene, hogy monoton legyen a b sorozat? felett? Miért ne ugrálhatna (pozitív és negatív értékekre) és főleg, miért kellene, hogy monoton legyen a b sorozat?
|
| Előzmény: [1688] Sirpi, 2007-01-04 23:47:54 |
|
|
| [1691] nadorp | 2007-01-06 12:56:32 |
 Legyen bn=an+2an+1. Ekkor
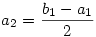
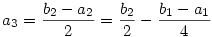
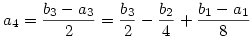
...
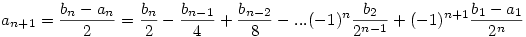 . .
Mivel 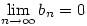 , ezért n>N esetén |bn|< , ezért n>N esetén |bn|< , azaz , azaz
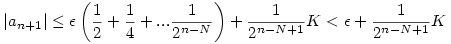 , ahol K a |b1-a1|,|b2|,|b3|... egy közös felső korlátja. ( Ez létezik, mert bn konvergens). Innen már látszik, hogy , ahol K a |b1-a1|,|b2|,|b3|... egy közös felső korlátja. ( Ez létezik, mert bn konvergens). Innen már látszik, hogy 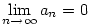
|
| Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16 |
|
|
|
| [1688] Sirpi | 2007-01-04 23:47:54 |
 Igaznak tűnik :-)
Tegyük fel, hogy an nem azonosan 0 egy adott indextől kezdve, és teljesül rá a feltétel. Cseréljük ki an-et egy bn sorozatra úgy, hogy bn=an, ha n páros, és bn=-an, ha n páratlan. Ekkor a feltétel ekvivalens bn/2-bn+1 konvergenciájával (ezzel egyszerűbb talán dolgozni, mert nem "oszcillál").
Legyen  >0. Ekkor a konvergencia miatt van olyan N, hogy minden n>N-re |bn/2-bn+1|< >0. Ekkor a konvergencia miatt van olyan N, hogy minden n>N-re |bn/2-bn+1|< . .
Mivel bn nem azonosan nulla valamilyen indextől, ezért van olyan m>N, amire bm 0 (feltehetjük, hogy pozitív, különben a bn sorozat helyett vegyük az ellentettjét). Ekkor bm/2- 0 (feltehetjük, hogy pozitív, különben a bn sorozat helyett vegyük az ellentettjét). Ekkor bm/2-  bm+1 bm+1 bm/2+ bm/2+ , vagyis (és ez a lényeg) a sorozot bm-től kezdve előbb-utóbb bemegy a [-3 , vagyis (és ez a lényeg) a sorozot bm-től kezdve előbb-utóbb bemegy a [-3 ;3 ;3 ] intervallumba, és onnan már nem is tud kijönni, így 3 ] intervallumba, és onnan már nem is tud kijönni, így 3 -hoz van megfelelő N' korlát. -hoz van megfelelő N' korlát.
Az, hogy ha bemegy, akkor nem tud kijönni, triviális, hiszen 0/2-  bn+1 bn+1 3/2 3/2 + + , azaz a következő elem abszolútértéke 5/2 , azaz a következő elem abszolútértéke 5/2 lesz maximum. Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 lesz maximum. Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2 -nál nagyobb értékhez nem tud konvergálni. -nál nagyobb értékhez nem tud konvergálni.
Tudom, ez így kicsit kusza, meg hosszú volt, de már kezd késő lenni. Nem tudom, van-e sokkal egyszerűbb(en leírható) megoldás.
|
| Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16 |
|
| [1687] Lóczi Lajos | 2007-01-04 22:25:16 |
 Bizonyítsuk be vagy cáfoljuk meg az alábbi állítást:
"Ha an egy olyan korlátos valós számsorozat, amelyre an+2an+1 nullához tart, akkor an konvergens" (és ekkor persze maga is nullsorozat).
|
|
|
|
|
|
|




 0 és f(x)=-1,x
0 és f(x)=-1,x




 minden n>N-re a folytonosság miatt, ezért bn/2-
minden n>N-re a folytonosság miatt, ezért bn/2- bn+1
bn+1 3
3 , azaz
, azaz  0 és így an
0 és így an