|
| [1742] Roberto85 | 2007-01-14 19:41:10 |
 Látom én h szépen kiszámoltátok őket, nagyon köszönöm is... csak hát kicsit kuszán vannak a feladatok...
de pl ezt a szinuszosat meg a 3szögeset fullra nem értem... szval én már a kezdésnél csak lesek, azt se tudom h melyik feladat hol kezdődik :( pedig nem vagyok segg hülye matekból csak hát nekem ezek már nehéz feladatok amúgy tényleg nagyon köszi
|
|
| [1741] Sirpi | 2007-01-14 17:56:02 |
 Szerintem játsszuk azt, hogy írd le, hogy Te melyik lépéseket nem érted, és azt majd elmagyarázzuk. De miután ilyen szépen ki lett fejtve minden feladat megoldása, tényleg nem baj, ha egy kicsit Te is dolgozol :-) Szóval várjuk a konkrét kérdéseidet.
|
| Előzmény: [1740] Roberto85, 2007-01-14 17:10:34 |
|
| [1740] Roberto85 | 2007-01-14 17:10:34 |
 bocsi de tényleg nem értem, mert elég összevissza vannak a feladatok... és ha valamit rosszul írok le akkor levágják h nem én csináltam! Meg amúgy is bele szokott kérezni, szval nagyon megköszönném ha írnál mellé egy kis magyarázó szöveget
|
|
| [1739] Roberto85 | 2007-01-13 21:45:48 |
 húúúha nekem itt nagyon összekeveredtek a dolgok h melyik melyik feladat :D megtudnád tenni h mind a 3 feladatot leírod egyszerre? :D
és a sin-os cos-os, és ezt a 3szögeset elmagyaráznád? mert ha belekérdez elég hülyén veszi ki magát h nem tudom :)
eddigiekért is nagyon köszi :)
|
|
|
| [1737] S.Ákos | 2007-01-13 19:16:02 |
 2. A térfogat:
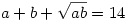
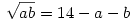
ab=196+a2+b2-28(a+b)+2ab
-ab=196+a2+b2-28(a+b)
ezt (1)-hez adva:
a2+b2=280+a2+b2-28(a+b)
a+b=10
innét 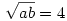
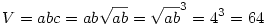
(a téglaest élei 2,4,8 egységnyiek, ezt az ab=16 a+b=10 egyenletrendszer megoldásával nyerhetjük)
|
| Előzmény: [1735] S.Ákos, 2007-01-13 14:12:07 |
|
|
| [1735] S.Ákos | 2007-01-13 14:12:07 |
 Ennyire jutottam eddig:
1. L melyik oldallal szembeni szöget jelöli?
2. Legyenek a téglatest élei a, b, c, és legyen 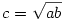 ! Ekkor felírható: ! Ekkor felírható:
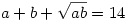
vagyis
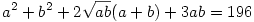
ebből kivonva (1)-et
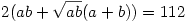
-Ennyi a téglatest felszíne.
3. Ismeretes, hogy cos2x+sin2x=1, így az egyenlet sin2x=y helyettesítéssel 4y+41-y=4alakba írható, innét: 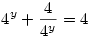 . Most legyen 4y=z, így az egyenlet . Most legyen 4y=z, így az egyenlet
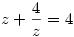
alakot ölt. Ennek megoldása az z=2, így
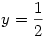
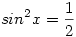
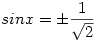
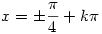
|
| Előzmény: [1734] Roberto85, 2007-01-13 11:06:32 |
|
| [1734] Roberto85 | 2007-01-13 11:06:32 |
 hello kaptam pár feladatot matekórán ha segítenétek megoldani őket nagyon megköszönném. Előre is köszi /sűrgős lenne/
Bizonyítsd be, hogy ha egy háromszögben L= 120 fok, akkor c(a2-c2)=b(a2-b2)
Egy téglatest egy csúcsból kiinduló éleinek összege 14, négyzetük összege 84. Egyik él mértani közepe a másik kettőnek. Mekkora a téglatest felszíne és térfogata?
|
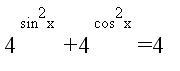 |
|
| [1733] Cckek | 2007-01-13 00:52:24 |
 Áltlánosítok mert két számra megoldottam. Tehát azt a legkissebb k-t keressük, hogy mindig kiválasztható legyen közüle p szám,(p adott) úgy hogy ezek közé elhelyezhetőek legyenek a + illetve - műveletek úgy hogy az eredmény osztható legyen n-nel.
|
| Előzmény: [1732] Cckek, 2007-01-13 00:07:19 |
|
| [1732] Cckek | 2007-01-13 00:07:19 |
 Nos jó... Akkor egy kis matematika. Ismert dolog, hogy 5 természetes szám közül mindig kiválasztható 2 úgy, hogy a különbségük, vagy összegük osztható legyen 7-tel. Akkor általánosítsuk ezt. Adott n esetén, határozzuk meg azt a k-t, hogy k szám közül mindig kiválasztható legyen 2 melynek a különbsége vagy összege osztható legyen n-el. Pl n=9-re k=6. Ez nagyon érdekes, mert k nyilván függ n-től, de kérdés hogy megadható-e zárt formában?
|
|
| [1731] rizsesz | 2007-01-12 19:09:42 |
 Nem tudom, hogy miért baj az, ha valaki felnéz valakire, és miért kell ezt nyalizásnak minősíteni. Attól még, hogy itt egyenlő félként, mindenki matematikával foglalkozik, még megadhatjuk egymásnak azt a jogot, hogy emberként viselkedünk egymással, és ha valaki segít nekünk, és veszi a fáradtságot, és pl. javaslatot tesz valamire, vagy neadjisten, még azt is megmondja, hogy hogyan kell valamit TeXben megírni, akkor azt nem kioktatásnak vesszük. Már ha ez lehetséges.
|
| Előzmény: [1730] Cckek, 2007-01-12 16:59:57 |
|
| [1730] Cckek | 2007-01-12 16:59:57 |
 Ugyan nem fogom már a topic témáját megváltoztatni, de azt már hadd döntsem én le, hogy kire nézek fel:)). Amúgy privátba nyalizz ez a topic itt a matematikáról szól, vagy legalábbis azt hittem eddig.
|
| Előzmény: [1728] nooby, 2007-01-12 14:25:42 |
|
| [1729] HoA | 2007-01-12 16:15:36 |
 Akkor konkrétan:
Állítás: Ha 2x-1 osztója 2p-1 -nek, akkor x megfelel.
Ebből az is következik, hogy
a) a legkisebb x>1 -et a legkisebb 2x-1 > 1 alakú osztóból kapjuk - és mind ilyen alakú.
b) Minden p-hez van x - ha kisebb nem, akkor p maga.
Bizonyítandó az Állítás és esetleg a fordítottja is.
|
| Előzmény: [1728] nooby, 2007-01-12 14:25:42 |
|
| [1728] nooby | 2007-01-12 14:25:42 |
 Cckek: Szerintem Sirpi nem kiosztani akart, csak jelezte, hogy szebben is beírhatnám a feladatot. Véleményem szerintem jogos volt. Egyébként meg mindkettőnknek van oka felnézni Rá ;) (Nézd meg az infot Róla, ha másképp vélekedsz!)
HoA: Ezt a 2p-1 osztóit kereső megoldást én is megtaláltam, azért tettem fel a kérdést, mert reméltem, hogy Ti tudtok rá valami mást mondani. Egyébként gratulálok!
U.i.: Sirpit már csak azért is meg kell védenem, mert én is majdnem ott fogok (remélhetőleg) diplomát szerezni, ahol Ő :)
|
| Előzmény: [1725] Cckek, 2007-01-12 13:12:23 |
|
| [1726] Sirpi | 2007-01-12 13:28:54 |
 Bocs, ha kioktatásnak érezted, igazából csak azért írtam le, hátha többen látják, hogy nem ördöngösség ez, és bátran lehet használni. Szebb is lesz a végeredmény, meg az illető is nagyobb lelki nyugalommal posztolhat tudván, hogy nem értik félre.
Bocs, ha kioktatónak tűntem, nem fogok ilyen hsz-t gyakran hegeszteni...
|
| Előzmény: [1725] Cckek, 2007-01-12 13:12:23 |
|
| [1725] Cckek | 2007-01-12 13:12:23 |
 Még jó, hogy ez a forum arról szól, hogy a matematikában érdekeltek, egyenrangú félként megbeszéljenek, megvitassanak dolgokat, esetleg segítsenek egymásnak bizonyos problémák megoldásában, és nem arról, hogy hogyan kell mindenkit kioktatni!:))
|
| Előzmény: [1727] Sirpi, 2007-01-12 10:53:42 |
|
| [1727] Sirpi | 2007-01-12 10:53:42 |
 Ajánlom figyelmedbe (és mindenki más figyelmébe is) a fórumhoz készített TeX-tanfolyamot-ot.
a b: $a \neq b$ b: $a \neq b$
a b: $a \equiv b$ b: $a \equiv b$
És amit még furán szoktak használni (*-gal):
a.b: $a \cdot b$
Szerintem nagyon hamar bele lehet szokni a dologba. Szóval az eredeti feltétel így néz ki TeX-ben:
p 2x2mod 4x-2, x 2x2mod 4x-2, x 1 1
$p \equiv 2x^2 \mod 4x-2$, $x \neq 1$
|
| Előzmény: [1721] nooby, 2007-01-11 18:25:31 |
|
| [1724] HoA | 2007-01-12 09:00:02 |
 Azt hiszem megvan a megoldás. Nem akarom ellőni, ezért egyelőre csak ennyit : Keressetek öszefüggést 2p-1 legkisebb valódi osztója és a p-hez található legkisebb x > 1 között.
|
| Előzmény: [1723] nooby, 2007-01-11 20:57:44 |
|
| [1723] nooby | 2007-01-11 20:57:44 |
 Nézzük a p=8 esetet. Ekkor szerintem az x=2 a legkisebb, mivel: 8 kongruens 8 (mod 4*2-2), de ha kipróbáltok más p-ket, akkor látszik, hogy változó, hogy mi lesz az optimális x értéke. Ha gondoljátok írhatok még néhány (p, x) párt...
|
| Előzmény: [1722] jenei.attila, 2007-01-11 20:37:24 |
|
|
| [1721] nooby | 2007-01-11 18:25:31 |
 Nos, jutott valaki tovább esetleg? Egyébként az, hogy valaki nem vette észre, hogy az egyet nem tekinti a feladat megoldásnak, az valószínű az én hibám, mert én nem tudok ilyen matematikai kifejezéseket írni, mint nemegyenlő, kongruens... ezért inkább máshogy próbálom ezeket olvasható formába önteni.
Különben a feladat megoldásának nem muszáj egy zárt képletnek lennie. Elég az, ha egy (asszimptotikusan) jobb algoritmust mond valaki ennél: for(int i=2; (...); i++) . Remélem, sokat segítettem ;)
|
| Előzmény: [1720] HoA, 2007-01-11 17:16:36 |
|
|
|





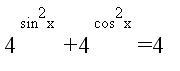


 b: $a \neq b$
b: $a \neq b$  b: $a \equiv b$
b: $a \equiv b$