| [1768] Roberto85 | 2007-01-17 13:07:10 |
 2. feladat Az alábbi négy kártyát látjuk, [1] [2] [3] [4] Mindegyik kártya mindkét oldalán 1-1 számjegy áll az 1-2-3-4 közül. LEgkevesebb hány kártyát kell megfordítani h eldöntsük: igaz e mind1ik kártyáára a következő állítás: Ha a kártya egyik oldalán 2es áll akkor a másik oldalán 4es?
|
|
| [1767] Roberto85 | 2007-01-17 13:04:11 |
 1feladat a, Van egymás mellett 5 ház, mind az 5 különböző színű b, A házakban egy egy személy lakik, mind különböző nemzetiségű c, MIndegyik fogyaszt valamilyen italt, dohányárút és tart valamilyen álatot. d, Egyikük sem fgyaszt ugyanolyan italt, szív ugyanolyan cigit, és tart ugyanolyan állatot.
Egyéb információk: 1. Brit piros házban lakik 2, svéd kutyát tart. 3. Dán teát iszik 4. fehér ház balján a zld ház van. 5, a zöld házban kávét fogyasztanak. 6. Az a személy aki Pall mallt szív, madarakat tart. 7. sárga ház lakója Dunhillt szív 8. Középső házban lakó tejet iszik 9. norvég az első házban lakik. 10.a Blendet szívó szomszédjában lakó macskát tart. 11. A blue mastert szívó ember sörözik 12.A lovakat tartó szomszédjábanlakó Dunhillt szív. 13. A német Prince-t szív 14. A norvég a kék ház szomszédja 15A blendet szívó ember szomszédjban vizet isznak
|
|
| [1766] Sirpi | 2007-01-17 07:56:06 |
 Ha jól értem, mivel kötött a menetrend, ezért tesszük fel, hogy az [a,b] intervallum fix. Viszont akkor az egyszerűség kedvéért legyen [a,b]=[0,1], a két város távolsága s, a vonat maximális gyorsulása pedig L (tehát [0,1]-en |f'(x)| L). L).
Nézzük meg, hogy maximálisan mekkora utat tud a vonat megtenni az adott idő alatt. Nyilvánvalóan az a legjobb stratégia, ha azonnal maximális gyorsításra kapcsol félútig, majd onnan maximális lassulásba kezd az út végéig. Az ehhez tartozó sebességgrafikon egy olyan egyenlő szárú háromszög két szára lesz, aminek a magassága L/2. És azért nyilvánvaló, hogy az ehhez tartozó út a maximális, mert az alatta lévő terület adja meg a megtett utat, és az összes többi stratégia grafikonja bele kell, hogy essen ebbe az egyenlő szárú háromszögbe.
A háromszög területe L/4, így rögtön adódik feltételként, hogy L 4s kell ahhoz, hogy a feladat megoldható legyen. 4s kell ahhoz, hogy a feladat megoldható legyen.
* * *
Most toljunk a háromszög felső csúcsától kezdve lefelé egy vízszintes egyenest. Ez elmetszi a két szárat, és a felső kis háromszöget figyelmen kívül hagyva egy egyenlő szárú trapézt kapunk a víszintes egyenes minden helyzete esetén. Állítsuk be úgy a felső egyenest, hogy a trapéz területe éppen s legyen. Megintcsak könnyen látható, hogy ez az optimális stratégia ahhoz, hogy a vonat maximális sebessége minimális legyen. Ugyanis tegyük fel, hogy van egy ennél is jobb. Ekkor ennek grafikonja végig a konstruált trapéz alatt kell, hogy haladjon - egyenlőség persze megengedett (a szárak fölé nem tud menni, mert akkor L-nél jobban gyorsulna, a felső vízszintes szakasz fölé megintcsak, mert akkor a maximális sebessége lenne nagyobb, mint a konstruált esetben). Viszont ekkor a görbe alatti terület kisebb kell legyen, mint a trapézé, vagyis a vonat nem éri el a célállomást, ami ellentmondás.
A max. sebesség minimuma könnyen ki is számolható: tegyük fel, hogy a vonat x idő után kezd állandó sebességgel haladni (és ekkor nyilván 1-x-nél kezd lassítani). A megtett út ilyenkor: L/4-(1-2x)2.L/4=s, vagyis 4x-4x2=4s/L, tehát x2-x+s/L=0. Innen
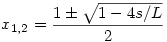
Ebből a kisebbre van szükségünk, a nagyobbik pont azt adja meg, hogy mikor kell lassítanunk.
* * *
A másik eset az, amikor a maximális sebesség maximalizálására törekszünk. Ekkor vegyük azt a stratégiát, amikor 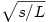 ideig maximálisan gyorsítunk, majd ugyanennyi idő alatt megállunk. ideig maximálisan gyorsítunk, majd ugyanennyi idő alatt megállunk. 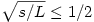 a feltételek szerint, tehát ez egy megvalósítható stratégia. Ilyenkor a megtett út a feltételek szerint, tehát ez egy megvalósítható stratégia. Ilyenkor a megtett út 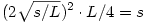 . Minden más stratégia viszont, aminél a maximális sebesség nagyobb, mint jelen esetben, szükségképpen több utat jelent, hiszen ha a(z egyik) maximális sebességű pontból L és -L meredekségű félegyeneseket húzunk lefelé, akkor az teljes egészében az eredeti út görbéje alatt kell hogy elhelyezkedjen a maximális gyorsulás miatt, és a félegyenesek által kifeszített háromszög is nagyobb területű lesz, mint s (a háromszög nagyobb magassága miatt), ami ellentmondás. Vagyis megkaptuk a maximális sebesség maximumát is. . Minden más stratégia viszont, aminél a maximális sebesség nagyobb, mint jelen esetben, szükségképpen több utat jelent, hiszen ha a(z egyik) maximális sebességű pontból L és -L meredekségű félegyeneseket húzunk lefelé, akkor az teljes egészében az eredeti út görbéje alatt kell hogy elhelyezkedjen a maximális gyorsulás miatt, és a félegyenesek által kifeszített háromszög is nagyobb területű lesz, mint s (a háromszög nagyobb magassága miatt), ami ellentmondás. Vagyis megkaptuk a maximális sebesség maximumát is.
Ha gond lenne az, hogy a vonat előbb ér az állomásra, mint kellene neki, akkor megtehetjük, hogy a konstruált háromszög területét nagyon picit csökkentjük, és a lassítási ág legvégén nagyon lassan gurulva tesszük meg az út utolsó 1 cm-ét (de ez már csak finomkodás).
* * *
Végeredmény:
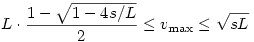
|
| Előzmény: [1764] Lóczi Lajos, 2007-01-17 01:52:30 |
|
| [1765] Lóczi Lajos | 2007-01-17 02:34:28 |
 Kicsit pontosabban megfogalmazva, a kérdést úgy akarom feltenni tehát, hogy mi lehet a maximális sebesség minimuma, illetve maximuma a megengedett sebességfüggvények halmazán. Tehát ez egy feltételes minimax és "maximax" feladat.
|
| Előzmény: [1764] Lóczi Lajos, 2007-01-17 01:52:30 |
|
| [1764] Lóczi Lajos | 2007-01-17 01:52:30 |
 Egy utazásom alkalmával jutott eszembe ez a teljesen gyakorlati kérdés -- számomra nagyon nehéznek tűnik, leginkább variációszámítás-ízű. Ezért nyugodtan tegyünk mindenféle egyszerűsítő feltevéseket, hogy bármiféle eredményt kapjunk. Tehát:
Adott két város, köztük egyenes vonalú pályán egy vonat fut. A két végállomáson a vonat sebessége persze nulla, menet közben a gyorsulás és lassulás természetesen korlátozott. A két város távolsága adott, a távolság megtételéhez szükséges idő szintúgy. A kérdés az, hogy mi lehet a vonat maximális sebessége, illetve ennek alsó/felső becslése.
Vegyünk fel adatokat tetszés szerint, hogy érdekes feladatokat kapjunk, mindenféle részeredményre kíváncsi vagyok.
Egy lehetséges modell a következő: adott egy f:[a,b] R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n. R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n.
|
|
| [1763] rizsesz | 2007-01-16 23:03:25 |
 Szóval nekem az lenne a kérdésem Roberto, hogy ezek a feladatok mihez segítenek hozzá, mármint ha megoldod őket, és beadod? Ismered azt, akinek odaadod?
|
|
| [1762] rizsesz | 2007-01-16 22:59:41 |
 Azért ha az egyenlet-rendezés nem megy, az azért elég aggasztó, nem? Mármint így mi értelme van a feladatok megoldását megadni?(moderáljatok engem!).
|
|
| [1761] Lacczyka | 2007-01-16 22:08:03 |
 Szerintem olvasd át S. Ákos [1737]-ben leírt megoldását. Ebben a végén kijönnek az oldalak, és ebből már nem gond sem a felszín, sem a térfogat kiszámítása. A másik megoldás (az csak a felszínre volt) a Te szempontodból nem lényeges. Viszont ha valamit nem értessz ebből a megoldásból [1737], akkor kérdezz rá konkrétan, sorra pontosan.
Lacczyka
|
| Előzmény: [1760] Roberto85, 2007-01-16 19:27:31 |
|
|
| [1759] Roberto85 | 2007-01-16 17:17:48 |
 még lenne egy kérdés, h amikor ki kell vonni az a2+b2+ab=84et, máskor meg hozzáadni, na ez miért kell?
|
|
| [1758] Csimby | 2007-01-16 16:59:09 |
 Nézheted fentről le is, no: c(a2-c2)=b(a2-b2) - ezt akarjuk bizonyítani. Most a2 - helyére beírjuk b2+bc+c2-t mindkét oldalon, (koszinusz tételből tudjuk hogy ezt megtehetjük) így ezt kapjuk: c(b2+bc+c2-c2)=b(b2+bc+c2-b2) Itt most egyszerűsítesz a zárójeleken belül, marad: c(b2+bc)=b(bc+c2) Kiemelsz baloldalból b-t, jobb oldalból c-t és ami marad: bc(b+c)=bc(b+c) Ami pedig nyilván igaz, így a bizonyítandó állítás is igaz volt, hiszen végig ekvivalens átalakításokat végeztünk.
|
| Előzmény: [1738] S.Ákos, 2007-01-13 19:23:33 |
|
| [1757] Roberto85 | 2007-01-16 16:44:24 |
 hát nézem visszafele, dehát nemértem ezt azért tényleg jó lenne ha elmagyaráznátok mindent lépésről lépésre...
|
|
|
| [1755] Csimby | 2007-01-16 16:25:42 |
 [1738]-nél alulról indulj ki és úgy következnek egymás utána a lépések felfelé, míg végül megkapjuk a bizonyítandó állítást. Utolsó lépésben felhasználjuk a2=b2+bc+c2-et is.
|
| Előzmény: [1753] Roberto85, 2007-01-16 15:55:26 |
|
|
| [1753] Roberto85 | 2007-01-16 15:55:26 |
 Felírva a koszinusz-tételt az a oldalra kapjuk, hogy
a2=b2+bc+c2 és ezutánni részt nem értem h jön ide, hogy c(a2-c2)=b(a2-b2) meg hogy ezután még ebből hogy lesz c(b2+bc+c2-c2)=b(b2+bc+c2-b2) azet a két lépést mondjátok el, azután nem zaklatlak benneteket :)
|
|
|
| [1751] Roberto85 | 2007-01-16 14:09:14 |
 amúgy vannak még feladataim :) 1. Egy gömb felületén véletlenszerűen választunk 3 pontot, mennyi a valószínűsége, h a választott pontok egy félgömbön lesznek?
2. Létezhet e olyan test, melynek oldalnézete négyzet, elölnézete háromszög, felülnézete kör :)
3. Körülbelül hány tonna követ használtak fel a Kheposz piramis építői (a mészkő sűrűsége 2,7 tonna köbméterenként) Kheposz fáraó 23 évig uralkodott. Hány köbméter követ kellett megmozgatniuk naponta, ha feltételezzük h 23évig épült? csak ennyi van megadva :S
|
|
|
|
| [1748] Roberto85 | 2007-01-16 12:26:35 |
 de pl a cosinus és sinusos fealdatnál amikor 4 az alapja. na szval annak a végén a megoldásnak van bent valami k betű az ott mi lenne? mert nekem a kerület ugrik be így elsőre...
|
|
| [1747] Roberto85 | 2007-01-15 19:29:07 |
 tenném én fel, de hát nem látom gybe a feladatokat...
|
|
| [1746] Sirpi | 2007-01-15 18:41:15 |
 Na, végre egy konkrét kérdés :-)
A koszinusz-tétel szerint minden háromszögben a2=b2+c2-2bccos  . És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-) . És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-)
|
| Előzmény: [1745] Roberto85, 2007-01-15 17:25:22 |
|
| [1745] Roberto85 | 2007-01-15 17:25:22 |
 meg hát főleg az lenne a kérdés h amikor bizsonyítani kell a 3szögesnél hova lett a 120fok?
|
|
|




 L).
L).  4s kell ahhoz, hogy a feladat megoldható legyen.
4s kell ahhoz, hogy a feladat megoldható legyen. 
 R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n.
R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n.
 szerint periodikus, így ha találunk egy megoldást, akkor ahhoz 2
szerint periodikus, így ha találunk egy megoldást, akkor ahhoz 2 . És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-)
. És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-)