| [1817] tomii282 | 2007-01-26 20:36:12 |
 A termeszetes szamok halmazan ertelmezett f fuggvenyre teljesul a kovetkezo feltetel: f(1)+2f(2)+...+nf(n)=[n(negyzeten)*(n+1)]/2*f(n),barmely n>=1 eseten, ha f(1)=2006,szamitsuk ki az f(2006) erteket
|
|
| [1823] Lacczyka | 2007-01-26 20:33:19 |
 A kalózos feladat más.
Van 10 kalózunk, akik szereztek száz aranyat, és egy sajátos osztozkodási eljárással osztják szét. sorba állítják magukat elvetemülség alapján, és a legelvetemültebb kalóz tesz egy osztozkodási ajánlatot: megmondja, hogy ki mennyit kap a 100 aranyból. Ezek után a kalózok szavaznak, és ha megvan az 50% (nem kell +1) akkor elfogadák, és úgy lesz. Ha nem fogadják el, akkor tengerbe dobják az illetőt, és a második legelvetemültebb tehet javaslatot, és így tovább. A kalózok döntési elvei: 1)leginkább életben akarnak maradni. 2) pénzéhesek, vagyis úgy döntenek, ahogy több arany üti a markukat. 3) vérszomjasak: ha nem származik hátrányuk egy társuk halálából, akkor automatikusan nem szavazzák meg a javaslatát. Kérdés: hány aranyat tud megtartani magának a legelvetemültebb rabló? Egyáltalán, életben maradhat? A feladat megítélésem szerint nagyon jó... ha nem ismerted, akkor határozottan ajánlom figyelmedbe :)
Üdv: Lacczyka
|
|
|
| [1815] HoA | 2007-01-26 14:39:32 |
 Osztozkodásból a "három rabló osztozik egy halom aranyporon" ismerős, ahol
- az arany tetszőleges finomsággal osztható
- mérleg nincs
- az igazságosság mércéje a kitűzésben meg van adva: a két rablóra működő egyik felez - másik választ elv
Ha ez a kalózos más, például 100 diszkrét aranyérméről van szó - akkor kérem a szövegét vagy elérhetőségét.
|
| Előzmény: [1814] Lacczyka, 2007-01-25 21:54:42 |
|
| [1814] Lacczyka | 2007-01-25 21:54:42 |
 Hálás köszönet a feladatért! Én az oroszlános feladaton kívül csak a "kalózok osztozkodnak a 100 aranyon" feladatot ismertem, és úgy éreztem, hogy ebben a témakörben fejlesztésre szorul a "feladat-táram". Mégegyszer köszi mindenkinek!
Üdv: Lacczyka
|
| Előzmény: [1813] rizsesz, 2007-01-25 18:39:31 |
|
| [1813] rizsesz | 2007-01-25 18:39:31 |
 Lacinak:
http://www.diag.hu/fel.php?id=177
|
|
| [1812] Lacczyka | 2007-01-25 15:46:51 |
 Az említett feladatot nem ismerem, légyszi tedd fel ide, vagy küldd el mailben (lacczyka@freemail.hu). Előre is köszi szépen :)
|
|
|
| [1810] jonas | 2007-01-25 11:30:16 |
 Pontosan.
Továbbá van a csalfa nőknek egy változata gőzmozdonnyal, és egy sapkákkal. A sapkás változatot valamelyik Smullyan könyv is említi.
|
| Előzmény: [1809] HoA, 2007-01-25 10:29:44 |
|
|
|
| [1807] rizsesz | 2007-01-24 20:25:05 |
 Azt érdemes végiggondolni, hogy mi a helyzet akkor ha páros, vagy ha páratlan sok oroszlán van. Igazából ki kell találni, hogy 2 oroszlánnál mi van, és akkor ebből hogyan következtethető ki a 3 oroszlán helyzete, stb.
|
|
| [1806] Lacczyka | 2007-01-24 18:51:15 |
 Üdv!
Igazából segítséget szeretnék kérni. Még régen találkoztam ezzel a feladattal:
Egy szigeten él 23 oroszlán. Ezek az oroszlánok teljesen civilizáltak (egymást "élve" nem eszik meg), okosak (képesek elvont gondolkodásra), és nemutolsósorban nagyon éhesek, lévén hogy a szigeten rajtuk kívül nincsen semmi.
Néhány galád kutató kísérleti jelleggel elhelyez a sziget közepén egy adag mérgezett húst (a galád kutatók a feladat szempontjából nem ehetőek), és várják, hogy az oroszlánok megeszik-e. A méreg hatása az, hogy amelyik oroszlán megeszi, az elalszik, de nem hal éhen. Ha viszont elaludt, akkor inenstől kezdve őt is megehetik az oroszlántársai, ebben az esetben azonban az az oroszlán, aki megeszi őt, szintén elalszik. Röviden: ha egy oroszlán megeszi a mérgezett húst, akkor életben marad, viszont mostantól mérgezett húsként funkcionál.
Az oroszlánok okosak, tudják, hogy a hús mérgezett, és a következő elvek alapján döntenek: 1, semmilyen körülmények között nem akarnak megevődni, vagyis inkább éhenhalnak, minthogy valaki őket netán elfogyassza. 2, életben akarnak maradni, vagyis ha nem fenyeget veszély, akkor megeszik a húst, és elalszanak.
Mit fog tenni az az oroszlán, amelyik először ér oda a húshoz: megeszi-e, vagy sem?
A feladat nem túl nehéz. Igazából hasonló típusú feladatokat szeretnék gyűjteni. Hogyha van valakinek olyan feladata, ami ehhez megoldásában, vagy gondolkodásmódjában hasonlít, akkor az legyen szives elküldeni nekem.
Előre is köszi: Lacczyka
|
|
|
| [1804] sakkmath | 2007-01-22 11:22:22 |
 A komoly problémák után kikapcsolódásként következzék egy könnyedebb, humoros feladat, amely Áprilisi fejtörő címmel a KöMaL 1980/4. számában jelent meg Csirmaz Lászlótól.
|
 |
|
|
| [1802] epsilon | 2007-01-21 09:08:31 |
 Köszi Mindenkinek! Alaposan kimerítettétek a témát! ;-) Cchek: a két szöget x illetve y-ra nevezve, mindkét oldalt 4-gyel szorozva, a sin2x=2sinx×cosx alapján, nullára rendezve, két négyzetösszek különbsége szorzatra bomlik és ez a 2 eset áll elő: sin2x=-2ctgy illetve sin2x=2ctgy és most a sin2x-et a tangens felesképletekkel kifejezzük sin2x=2t/(1+t×t) ahol t=tgx és így t-ben másodfokú egyenlet lesz, szerinted ez az út nem járható?
|
|
| [1801] Lóczi Lajos | 2007-01-20 23:54:31 |
 A számítógép szépen végignézte az összes esetet, és persze megtalálta a (100,0,0,0,0,0), (50,50,50,50,0,0) optimumokat (és csak ezeket találta).
|
| Előzmény: [1799] HoA, 2007-01-20 19:43:10 |
|
| [1800] Lóczi Lajos | 2007-01-20 21:32:49 |
 Ó, persze, a nemnegativitási feltételeket kihagytam. Köszönöm, hogy rámutattál.
(Az zavarhatott meg, hogy egyenlőtlenséggel megadott feltételek esetén a multiplikátoroknak maguknak is nemnegatívnak kell lenniük, de ez még nem mond semmit a változókról...)
|
| Előzmény: [1799] HoA, 2007-01-20 19:43:10 |
|
| [1799] HoA | 2007-01-20 19:43:10 |
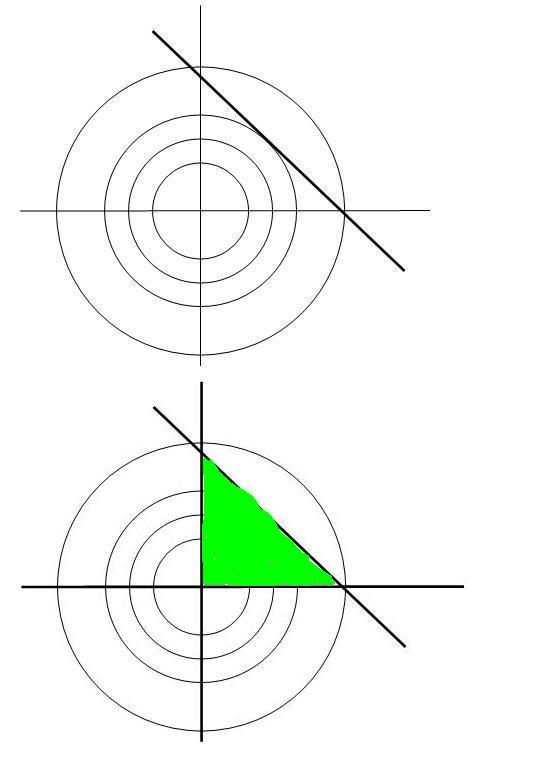
 A megfigyelt jelenség már akkor is előjön, ha csak az első feltételt vesszük. Legyen tehát
L(x,y, ):=x2+y2+ ):=x2+y2+ (100-x-y) (100-x-y)
Az első két parciális deriváltból itt is kijön x=y. Ábrázoljuk az f(x,y)=x2+y2 függvényt az xy síkban szintvonalakkal: ezek nyilván origó középppontú koncentrikus körök. A vizsgált tartomány az x+y=100 egyenes által határolt félsík. f(x,y) a tartományban és a határán is tetszőleges nagy értéket felvehet, maximuma nincs. Az egyenes x=0 vagy y=0 értékkel jellemzett pontja, amelyekből az y=100 ill. x=100 érték adódna, semmilyen különleges szerepet nem játszik. Nem is csoda, hiszen nemcsak x és y nagyságviszonyát, hanem az x 0 , y 0 , y 0 feltételeket sem vettük figyelembe. Ha megtesszük, a Lagrange függvény így alakul: 0 feltételeket sem vettük figyelembe. Ha megtesszük, a Lagrange függvény így alakul:
L(x,y, 1, 1, 2, 2, 3):=x2+y2+ 3):=x2+y2+ 1(100-x-y)+ 1(100-x-y)+ 2(x-0)+ 2(x-0)+ 3(y-0) 3(y-0)
A megoldandó egyenletrendszerben a 0-t adó szorzatoknál 0 tényezőül {100-x-y=0; 2=0;y=0} -t választva x = 100, {100-x-y=0;x=0; 2=0;y=0} -t választva x = 100, {100-x-y=0;x=0; 3=0} -ból y = 100 adódik. A { 3=0} -ból y = 100 adódik. A { 1=0;x=0;y=0} választás a megengedett 1=0;x=0;y=0} választás a megengedett  alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y 100 és z+t+u+w 100 és z+t+u+w 100 mellett a w 100 mellett a w 0 , u 0 , u w , t w , t u, ... , x u, ... , x y feltételeket is figyelembe kell venni. Ezzel egyúttal a változók nemnegatív voltát is biztosítjuk. A 8 db 0 szorzat 0 tényezőinek megválasztásánál - 28 eset - anélkül, hogy mind a 256 kombinációt végignéznénk, csak rámutatunk, hogy a { w=0; u=w ; t=u; z=t ; y =z ; x+y = 100 } választás adja az x=100,y=z=t=u=w=0 megoldást, míg a { w=0; u=w ; z=t ; y =z ; x+y = 100 ; z+t+u+w = 100 } kombináció az x=y=z=t=50,u=w=0 eredményt. y feltételeket is figyelembe kell venni. Ezzel egyúttal a változók nemnegatív voltát is biztosítjuk. A 8 db 0 szorzat 0 tényezőinek megválasztásánál - 28 eset - anélkül, hogy mind a 256 kombinációt végignéznénk, csak rámutatunk, hogy a { w=0; u=w ; t=u; z=t ; y =z ; x+y = 100 } választás adja az x=100,y=z=t=u=w=0 megoldást, míg a { w=0; u=w ; z=t ; y =z ; x+y = 100 ; z+t+u+w = 100 } kombináció az x=y=z=t=50,u=w=0 eredményt.
|
 |
| Előzmény: [1791] Lóczi Lajos, 2007-01-19 01:16:58 |
|
|
| [1797] HoA | 2007-01-19 23:04:07 |
 A módszer az alábbi általánosításig biztosan működik:
- a két csoportban szereplő számok darabszáma ( most 2, ill. 4 ) legyen k ill. m.
- a csoportok elemeinek összege ( most 100,100) ne legyen nagyobb, mint A ill. B
Tehát legyen k+m számunk, x1,...,xk+m , ahol
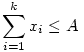 | (2) |
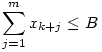 | (3) |
Mekkora 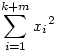 maximuma? maximuma?
Az összeget rögzített xk (az első csoport legkisebb eleme, az eddigi y) mellett vizsgáljuk. (1) -ből és (2) -ből 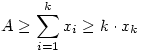 , , 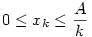 ( Ez egyben válasz Epsilon kérdésére: A=100 és k=2 esetére 0 ( Ez egyben válasz Epsilon kérdésére: A=100 és k=2 esetére 0 x2=y x2=y 50 ) Az [1795]-beli indokláshoz hasonlóan belátható, hogy az első csoport négyzetösszege akkor a legnagyobb, ha x2=x3=...=xk x1=A-(k-1).xk Példa: ha k=4,x4=4,A=22 , akkor { 10;4;4;4 } négyzetösszege nagyobb, mint pl. { 7;6;5;4 } -é. A második csoportra igaz az [1795]-beli szabály: ameddig lehet xk+j=xk egy szám pedig B és az eddigiek összegének különbsége: xk+1=xk+2=...=xk+d=xk,xk+d+1=B-d.xk Az [1795]-beli szakaszhatárok most a 50 ) Az [1795]-beli indokláshoz hasonlóan belátható, hogy az első csoport négyzetösszege akkor a legnagyobb, ha x2=x3=...=xk x1=A-(k-1).xk Példa: ha k=4,x4=4,A=22 , akkor { 10;4;4;4 } négyzetösszege nagyobb, mint pl. { 7;6;5;4 } -é. A második csoportra igaz az [1795]-beli szabály: ameddig lehet xk+j=xk egy szám pedig B és az eddigiek összegének különbsége: xk+1=xk+2=...=xk+d=xk,xk+d+1=B-d.xk Az [1795]-beli szakaszhatárok most a 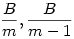 ... értékek. Vegyük észre, hogy ... értékek. Vegyük észre, hogy 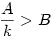 esetén xk>B is előfordulhat, tehát maga B is lehet szakaszhatár. Ekkor a második csoport első eleme B, a többi 0. Másrészt ha esetén xk>B is előfordulhat, tehát maga B is lehet szakaszhatár. Ekkor a második csoport első eleme B, a többi 0. Másrészt ha 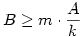 akkor a második csoportba mindig "belefér" m darab xk érték, tehát görbénk csak egyetlen parabolaívből áll. Függvénygörbénk - a maximális négyzetösszeg xk tól függése - vizsgálatát másokra hagyom. akkor a második csoportba mindig "belefér" m darab xk érték, tehát görbénk csak egyetlen parabolaívből áll. Függvénygörbénk - a maximális négyzetösszeg xk tól függése - vizsgálatát másokra hagyom.
|
| Előzmény: [1796] epsilon, 2007-01-19 17:09:25 |
|
| [1796] epsilon | 2007-01-19 17:09:25 |
 Helló HoA! Valóban elemi, logikus, szép. Van néhány kérdöjelem, amit magamban kellene tisztáznom: Az y nem több mint 50 az indulásból feltehető? Továbbá ha általánosítani kellene, a 100 helyett pl. 2a lenne, na meg a tagok száma 6 helyett n, akkor az általad jelzett 3 intervallumba sorolás az y-ra vonatkozóan hogyan alakulna, mindegyiket külön-külön elemezni kellene, vagy belátható-e elég könnyen, hogy a sok lokális maximumból melyik is a globális maximum? Én ezeken tűnődöm, ha vannak megjegyzéseid, szívesen veszem, és kösz, a megoldásodban volt jó pár mentő ötlet! Üdv: epsilon
|
|
| [1795] HoA | 2007-01-19 11:20:58 |
 Egy elemi eszközöket használó megoldás lépései:
Bontsuk a négyzetösszeget két részre, legyen az első tag x2+y2 , a második z2+t2+u2+w2 . Vizsgáljuk a maximumot rögzített y mellett (0 y y 50). Az első tag nyilván akkor a legnagyobb, ha x = 100 - y. A második tagban keressük négy 0 és y közötti z,t,u,w szám maximális négyzetösszegét, ahol z+t+u+w<=100 . 50). Az első tag nyilván akkor a legnagyobb, ha x = 100 - y. A második tagban keressük négy 0 és y közötti z,t,u,w szám maximális négyzetösszegét, ahol z+t+u+w<=100 .
1) Belátható, hogy ha z+t+u+w<100 és nem mindegyik = y, akkor az y-nál kisebb számok növelésével a négyzetösszeg nő.
2) Belátható, hogy rögzített z+t+u+w mellett a négyzetösszeg nő, ha egy nagyobb számot növelünk és egy kisebbet csökkentünk: Szabatosan : Ha z>t d>0, akkor (z+d)2+(t-d)2>z2+t2 d>0, akkor (z+d)2+(t-d)2>z2+t2
1) -ből és 2) -ből következik, hogy a második tag akkor a legnagyobb, ha z,t,u,w ameddig csak lehet = y , egy szám pedig a többiek 100-ból vett maradéka. Vagyis a második tag szerkezete függ y-tól. Szabatosan: Ha 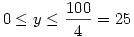 , akkor a második tag maximuma 4y2 , a két tag összege , akkor a második tag maximuma 4y2 , a két tag összege
. Ha 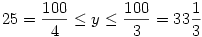 , akkor a második tag maximuma 3y2+(100-3y)2 , a két tag összege , akkor a második tag maximuma 3y2+(100-3y)2 , a két tag összege
| (100-y)2+4y2+(100-3y)2 | (2) |
. Végül ha 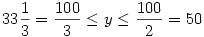 , akkor a második tag maximuma 2y2+(100-2y)2 , a két tag összege , akkor a második tag maximuma 2y2+(100-2y)2 , a két tag összege
| (100-y)2+3y2+(100-2y)2 | (3) |
A négyzetösszeg maximumot y függvényében ábrázolva tehát egy három, egymáshoz csatlakozó, alulról konvex parabolaívből álló görbét kapunk. A teljes y tartományra a maximumot ezért csak a széleken és a csatlakozási pontokban kell vizsgálni. természetesen a már ismert eredményt kapjuk: A maximum 10000, amit az x=100, y=z=t=u=w=0 és az x=y=z=t=50, u=w=0 értékrendszerek adnak.
|
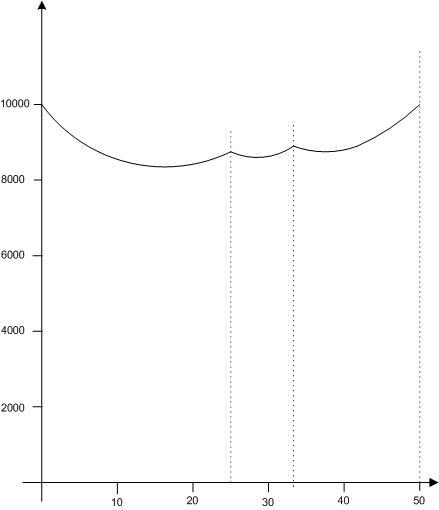 |
| Előzmény: [1792] epsilon, 2007-01-19 07:16:56 |
|
| [1794] epsilon | 2007-01-19 11:16:20 |
 Szerintem nem, mert ennél nem használtuk fel a betűk közötti rendezési sorrendet, és ha annélkül kijönne, akkor...nem stimmel mert a feltételek nélkül más értékekre nagyobb lehet a maximum. Vagyis akár rendezett sorrenddel, akár annélkül, nem jöhet ki ugyanaz.
|
|










 ):=x2+y2+
):=x2+y2+ 0 , y
0 , y alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y
alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y 100 és z+t+u+w
100 és z+t+u+w
 ,tg
,tg
 Q.
Q. 