| [18] Kós Géza | 2003-11-05 11:36:33 |
 Azt javaslom, hogy a megoldásokat is ide írjuk, ne tördeljük szét a témát többfelé. Én az emberevős feladatra kaptam egy megoldást e-mailben, mindjárt ide másolom.
|
|
| [17] lorantfy | 2003-11-05 10:21:31 |
 Segítség a biliárdgolyós feladathoz: 3 csoportra osztjuk a 12 golyót. Összemérjük az első két csoportot. Ha egyenlő akkor innen már 2 méréssel a könnyű a dolgunk, ha felhasználjuk, hogy az első 8 golyó biztosan "jó". Ha az első mérésnél nem egyenlő a két csoport akkor figyelembe véve, hogy a mérleg merre billent le egy különleges mérést kell összeállítanunk, ahol a mérleg kibillenésének irányából is információkat tudunk szerezni. Na erre kell neked rájönni!
|
|
| [16] SchZol | 2003-11-04 20:14:40 |
 Sziasztok!
Én már megoldottam a billiárdgolyós példát, pont ma jött meg Lórántfytól a könyv, amit felajánlott. Szívesen leírom a megoldásom, ha kell.
Üdv,
Zoli
|
|
|
| [14] Frenky | 2003-11-04 17:18:34 |
 Üdv! JAJJ ez a billiárdgolyós példa.... érmével ismerem de végülis teljesen mindegy vagy egy hétig gondolkoztam rajta de nem sikerült.... mondjuk helyenként már elég sokáig eljutottam, sőt azt hittem sikerült, de aztán persze nem... na ennek egyszer beírhatnánk a megoldását...:-) mert az életben rá nem jövök...
|
|
|
| [12] Kós Géza | 2003-11-04 14:53:11 |
 Szia Laci,
Jó kérdés. :-)
Szerintem nem mindegy, hogy ismered a feladatot és a megoldást, vagy te találod meg. Ha te oldod meg elsőnek, és beírod a megoldást, az egyfajta dicsőség, de az is igaz, hogy nem mindig jó túl hamar lelőni a megoldást. Ha viszont ismered és úgy lövöd le, akkor...
Talán úgy kellene felfogni, mintha egy asztaltársaságban ülnénk egy pofa sökóla mellett :-). Ott sem mindig jó azonnal bedobni a megoldást, hagyni kell a többieket is gonsolkodni.
Ha viszont egy feladatot régóta nem oldottak meg, akkor lehet kérni, hogy valaki, aki ismeri, írja le. Én már régóta várom, hogy a 4. feladatot megoldja valaki, mert van egy kicsit nehezebb változata is, amit szeretnék majd feladni.
Üdv.
Géza
|
| Előzmény: [11] enel, 2003-11-04 14:32:31 |
|
| [11] enel | 2003-11-04 14:32:31 |
 Sziasztok! Nekem egy régi problémám, hogy ha egy feladatnak tudom a megoldását (mindegy, hogy most oldottam meg vagy korábban) akkor mikor "illik" (ha egyáltalán illik) beírni egy fórumra. Utálom, ha hamar megmondják a megoldást, Magam szeretem megoldani a fejtöro"ket, feladványokat. Ez annyira így van, hogy ha egy vicc kérdéssel indul, akkor arra is próbálok "megfelelni". Mesélek egy példát: Két függvény sétál a sivatagban. Odaugrik a rablófüggvény és rájuk ordít. "Adjátok ide az értékkészleteiteket, mert különben lederivállak benneteket!" Erre az egyik függvény elkezd kuncogni. Miért?
|
|
| [10] Mate | 2003-11-04 13:05:56 |
 Sziasztok! Úgy látom, ma gyereknap van, úgyhogy ha valaki megcsinálja a novemberi számban kitűzendő elektrosztatika-feladatomat integrálszámítás nélkül, vendégem egy somlói galuskára, és megkapja a Rácz Béla által felajánlott tábla csokit (ugyanis a Tom and Jerry példát úgysem oldja meg senki...)Vigh Máté:))
|
|
| [9] Rácz Béla | 2003-11-04 00:33:05 |
 Jó, én pedig felajánlok minimum 1 tábla csokit annak, aki elsőként megoldja Kós Géza: Tom és Jerry c. feladatkölteményét (Kömal 2003/5.) - Természetesen csak akkor, ha nem maga Géza az illető.
|
|
|
|
| [6] SchZol | 2003-11-01 22:12:06 |
 5.feladat:
Adott 100 láda mindegyikben 1000db 2grammos 1 forintos, kivéve egyett amiben 1grammosak az 1 forintosok. Legkevesebb hány mérésből tudjuk eldönteni melyik ládában vannak a selejtes egy forintosok, ha minden láda ugyanúgy néz ki, és csak egy egykarú mérlegünk van.
Szívesen fogadom a megoldásokat emailben.
Zoli
|
|
| [5] lorantfy | 2003-10-31 23:34:57 |
 4.feladat: Van 12 db biliárdgolyó mindegyik ugyanolyan színű és formájú csak az egyiknek a súlya eltér a másiktól. Azt nem lehet tudni hogy könnyebb vagy nehezebb. A feladat a következő: Hogyan tudod megállapítani biztosan hogy melyik a kakukktojás, ha van egy kétkarú mérleged és csak 3-szor mérhetsz vele? Az első e-miles megoldónak Gazsó Zoltán: "Visual" Adatbázis kezelők objektum-orientált programozása c. könyvét tudom felajánlani vagy egy tábla csokit.
|
|
| [4] Lóczi Lajos | 2003-10-31 20:12:50 |
 Kedves Sirpi,
nem tudom, hogy eldöntöttétek-e már, ebbe a rovatba várjunk-e megoldásokat (vagy csak bizonyos idő után), esetleg nyissunk egy új témát külön a megoldásoknak, hogy ne lőjük le a poént...szóval ha van elképzelés erről bárki részéről, írja meg.
Lajos
|
| Előzmény: [1] Sirpi, 2003-10-30 10:07:33 |
|
| [3] Kós Géza | 2003-10-30 11:08:09 |
 3. feladat. Az Óperenciás tenger közepén áll az Emberevők Szigete. Ez a sziget kör alakú, s partja mentén pontosan 26 falu található, lakosaik pogányok. A falvak nevei sorra az angol ábécé 26 betűjével kezdődnek (ciklikus sorrendben). A szigetet történelme folyamán pontosan 26 angol hittérítő kereste fel, ezek nevei is az angol ábécé különböző betűivel kezdődtek. Minden hittérítő először abba a faluba ment, amely nevének kezdőbetűje az ő neve kezdőbetűjével megegyezett. A szigeten egyszerre több hittérítő is tartózkodhatott, de egy faluban egyszerre csak egy. Ha egy hittérítő olyan faluba ért, amelynek lakosai éppen pogány hiten voltak, akkor megtérítette őket, és tovább ment a tengerpart mentén a következő faluba úgy, hogy a tenger jobb kéz felől essen. Ha viszont megtérített faluba ért, akkor a falu lakosai visszatértek a pogánysághoz és felfalták a szerencsétlent.
A hittérítők sorsa nem kétséges, de vajon milyen hiten vannak a falvak a hittérítők működése után?
(A feladat a KöMaL 1983. áprilisi számában jelent meg.)
|
|
| [2] Fálesz Mihály | 2003-10-30 10:22:23 |
 Javaslom, hogy számozzuk a feladatokat, ahogyan az két azonos nevű uralkodótól (vagy éppen világháborútól) kezdve szokás. :-)
Szóval, hátha valaki nem ismeri ezt a több, mint száz éves feladatot, amely a nagy Samuel Lloydtól származik.
2. feladat. A képen 9 pont látható; egy négzet csúcsai, középpontja és oldalfelező pontjai. Rajzoljunk olyan folytonos töröttvonalat, amely csupán 4 (négy), egymáshoz csatlakozó szakaszból áll, és mindegyik ponton átmegy.
(Nem csalás, nem ámítás, ilyen töröttvonal tényleg létezik!)
|
 |
|
| [1] Sirpi | 2003-10-30 10:07:33 |
 Ha valakinek van valami jó matekpéldája, amit érdemesnek tart a többiekkel megosztani, akkor ide bátran beírhatja. Aktív KöMaL feladatokat légyszi ne irjatok be! Következzen elsőnek egy saját feladatom, azért is, hogy a TeX-et gyakoroljam: Biz. be: 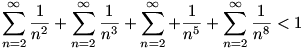
Sirpi |
|












