| [1893] Cckek | 2007-02-14 19:51:20 |
 Ez a feladat túl szép ahoz, hogy megoldatlanul maradjon:
a1 (0,1) Ha ak (0,1) Ha ak (0,1) akkor ak+1=ak2(ak-1)+1, de -1<ak-1<0 tehát 1-ak2<ak2(ak-1)+1<1 az-az ak+1 (0,1) akkor ak+1=ak2(ak-1)+1, de -1<ak-1<0 tehát 1-ak2<ak2(ak-1)+1<1 az-az ak+1 (0,1). A matematikai indukció elve szerint an (0,1). A matematikai indukció elve szerint an (0,1), (0,1), n n N. N.
an+1-an=an3-an2-an+1=(an-1)2(an+1)>0 tehát an növekvő. Legyen an határértéke l. Ekkor l=l3-l2+1,l [0,1] tehát l=1. Tehát létezik egy bn csökkenő sorozat, bn [0,1] tehát l=1. Tehát létezik egy bn csökkenő sorozat, bn 0 úgy hogy an=1-bn. Írhatjuk: 0 úgy hogy an=1-bn. Írhatjuk:
1-bn+1=(1-bn)3-(1-bn)2+1 bn+1=bn(1-bn)2 ezért bn+1=bn(1-bn)2 ezért
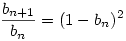
ahonnan tagonként felírva majd összeszorozva kapjuk, hogy
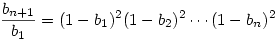 ahonnan ahonnan 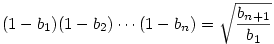 . .
Tehát
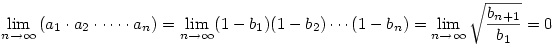
|
| Előzmény: [1890] Cckek, 2007-02-10 12:44:33 |
|
| [1892] jonas | 2007-02-12 18:03:59 |
 A feladatot nem találtam meg, de az állítást a Járai-könyvben igen (162. oldal).
Ez azt állítja, hogy a racionális számok halmaza nem áll elő megszámlálhatóan sok nyílt halmaz metszeteként.
|
| Előzmény: [1854] jonas, 2007-01-31 15:08:11 |
|
| [1891] HoA | 2007-02-10 16:32:44 |
 Mint matektanárunk szokta mondani, az eredmény közlése nem egyenlő a feladat megoldásával. Ha valakinek kell egy kis segítség az ilyen típusú feladatok megoldásához, hát lássuk: 1. megközelítés. Ki mond igazat?
I: Az első ajtó mond igazat -> a nyeremény a 2. mögött van -> a 2. is igazat mond -> ellentmondás azzal, hogy csak egy mond igazat
II: a második ajtó mond igazat -> mivel csak egy ajtó mond igazat, az 1. ajtó hazudik -> a 3. is igazat mond -> ellentmondás azzal, hogy csak egy mond igazat
III. a harmadik ajtó mond igazat -> mivel csak egy ajtó mond igazat, az 2. ajtó hazudik -> a nyeremény a 3. mögött van -> az 1. hazudik -> JÓ MEGOLDÁS
2. megközelítés: Hol a nyeremény?
I: Az első ajtó mögött -> 1. hazudik, 2. igazat mond, 3. igazat mond -> két igazmodó: ellentmondás
II: A második ajtó mögött -> 1. igazat mond, 2. igazat mond -> két igazmodó: ellentmondás
III: A harmadik ajtó mögött -> 1. hazudik, 2. hazudik, 3. igazat mond -> JÓ MEGOLDÁS
|
| Előzmény: [1889] Anum, 2007-02-10 11:00:54 |
|
| [1890] Cckek | 2007-02-10 12:44:33 |
 Az 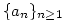 sorozat a következőképpen adott: sorozat a következőképpen adott:
a1 (0,1), an+1=an3-an2+1. (0,1), an+1=an3-an2+1.
Számítsuk ki a következő határértéket:
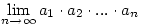 . .
|
|
|
| [1888] tim20 | 2007-02-10 10:28:37 |
 Sziasztok!
3 ajtó közül az egyik mögött nyeremény rejtőzik. Ám az ajtók közül csak az egyik mond igazat. Melyik ajtó mögött találod a nyerményed? 1.ajtó: "A 2-es mögött van." 2.ajtó: "Nem a 3-as mögött van." 3.ajtó: "Az 1-es hazudik!"
Lehetőségek:
1. ajtó 2. ajtó 3. ajtó nem lehet meghatározni, hogy melyik mögött van egyik mögött sincs
|
|
| [1887] Cckek | 2007-02-06 17:33:44 |
 Valóban szép interpolációs polinom, akkor az ajánlom szerkesszük meg trigonometrikus interpolaciós polinomját is, úgy hogy 1,2,3,...,8 helyeken a polinom ezeket az értékeket vegye fel:)
|
| Előzmény: [1886] HoA, 2007-02-06 16:48:13 |
|
| [1886] HoA | 2007-02-06 16:48:13 |
 Igazán díjazom a humorotokat, de azért ne hülyítsük az ifjúságot! LócziLajos rámutatott, hogy tetszőleges y1,y2,...,yk racionális értékekhez megadható olyan, legfeljebb k-1 -edfokú racionális együtthatós polinom, mely az 1,2, ... , k helyeken éppen az adott értékeket veszi fel ( vagy máshol, ld. második példa ) Ekkor persze mondhatjuk, hogy megvan a "szabály" , a sorozat folytatása a polinom következő egész helyeken felvett értéke.
Bohner Géza ötlete még keményebb, tkp. azt mondja, bármi megfelel, aminek az eleje megegyezik a megadottakkal. Mondjuk az adott számok Hófehérke és a hét törpe születésnapjának "nap" részei, és a következő szám a királyfi szülinapjának "nap"-ja. (Hogy ezeket honnan tudjuk, az más kérdés :-))
Félretéve a tréfát, nem mindig olyan egyértelmű rájönni az "igazi" szabályra, vagyis arra, amire a feladat kitűzője gondolt. Nekem már jött ki IQ-teszt -szerű feladatokban más "következő száma a sorozatnak" mint ami a megoldások között szerepelt, pedig igyekeztem a feladatkitűzők matematikai szintjére "emelkedni".
|
| Előzmény: [1884] BohnerGéza, 2007-02-06 12:42:04 |
|
|
| [1884] BohnerGéza | 2007-02-06 12:42:04 |
 Még az előző hozzászólásénál is egyszerűbb szabály!
Legyen a sorozat első nyolc tagja 1,4,9,7,7,9,13,10, majd a többi tetszőleges, például 77, 77, 77, ...
Azért a feladat feladója valószínűleg Cckek [1881]-ben adott válaszára gondolt!
|
| Előzmény: [1878] tim20, 2007-02-06 10:15:01 |
|
| [1883] Lóczi Lajos | 2007-02-06 12:12:31 |
 Inkább nekem higgyél! "Négyzetszámok", meg "számjegyek összege" ... brrr, de bonyolult. Vegyük csak az egyszerű racionális számokat és a polinomokat, hiszen már az ókoriak is...
1. Nézzük a
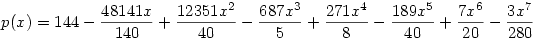
polinomot. Itt p(1)=1,p(2)=4,p(3)=9,...,p(8)=10. A 9. tag tehát -99 lesz, mert p(9)=-99.
Csak ez a megoldás lehet jó! Kipróbáltam ugyanis: vettem egy másik polinomot, mondjuk:
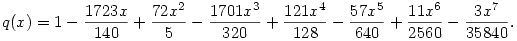
Nocsak! Páros helyeken tökéletes az egyezés: q(0)=1,q(2)=4,q(4)=9,...,q(14)=10. Mivel 14+2=16 és q(16)=-99, a sorozat 9. helyén álló szám tényleg a -99.
:-)
|
| Előzmény: [1878] tim20, 2007-02-06 10:15:01 |
|
|
|
|
| [1879] Sirpi | 2007-02-06 10:46:11 |
 ...9, 1, 4, 9, 16, 16, 9, 13, 19, 9, 10, 4, 9...
Egyelőre nem lőném le, annyi segítség, hogy az elejéből látszik, hogy a négyzetszámokhoz van köze a dolognak.
|
| Előzmény: [1878] tim20, 2007-02-06 10:15:01 |
|
| [1878] tim20 | 2007-02-06 10:15:01 |
 Sziasztok!
Találtam egy feladványt, de nem jövök rá a logikájára, pedig biztosan egyszerű. Szerintetek mi lesz a következő szám ebben a számsorban: 1,4,9,7,7,9,13,10, ?
Ugye valaki tud segíteni?
|
|
|
| [1876] Lóczi Lajos | 2007-02-06 02:52:19 |
 Ez a feladat nem más, mint apró általánosítása annak a jól ismert elemi állításnak, hogy egy konvergens sorozat limesze azonos a sorozatból képezett számtaniközép-sorozat limeszével.
Jelölje xn limeszét X, Y jelentése hasonló. Jelölje K a két sorozat abszolútértékének egy közös felső korlátját.
Nyilván azt kell igazolni, hogy
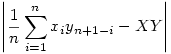
nullsorozat. De ezt -- az AB-CD=A(B-D)+D(A-C) összefüggés figyelembe vételével -- nyilván felülről becsülhetjük az alábbival:
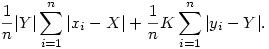
A befejezéshez elég megmutatni, hogy ezek nullsorozatok. Nyilván elég azt belátni, hogy ha xn X, akkor X, akkor 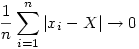 . .
Rögzítsünk egy  >0 számot, és legyen N( >0 számot, és legyen N( ) az a küszöbindex, melyre minden n>N( ) az a küszöbindex, melyre minden n>N( ) esetén |xn-X|< ) esetén |xn-X|< . Legyen n>N( . Legyen n>N( ). Ekkor ). Ekkor
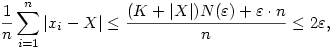
ha n elég nagy.
|
| Előzmény: [1874] Cckek, 2007-02-05 17:27:15 |
|
| [1875] pogre | 2007-02-05 17:41:49 |
 nah én tök béna vok a matekhoz tehát ne nevessetek ki a feladatommal!!! A sugarak intenzitása exponenciálisan csökken anyagokba való behatoláskor! 6mm mélységben az intenzitás az eredeti 10 százalékára csökken csökken!
a) Írj fel formulát az intenzitás csökkenésére b)mekkora lesz az intenzitás 2mm mélységben
|
|
|
|
| [1872] Cckek | 2007-02-05 16:59:26 |
 Találkoztam egy nagyon érdekes feladattal, persze nem tudom megoldani:(
Legyenek xn, yn konvergens sorozatok. Bizonyítsuk be, hogy
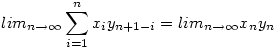
|
|
| [1871] Mhari | 2007-02-05 15:44:28 |
 Sziasztok!
Köszönöm Nektek - Lóczi Lajos és Cckek - a gyors megoldást,tetszik mindkettőtöké, de a lelkivilágomhoz mégis Cckek-é áll közelebb, az olyan "hagyományos", rendezgetős, számolgatós. Én próbálkoztam mindennel, ami a fejemből kifért, de erre az egyszerű dologra nem is mertem gondolni, hogy a 4xy így bontsam fel. Hát hiába, aki tud, az tud. Üdv: Attila
|
|
| [1870] Cckek | 2007-02-05 05:10:02 |
 A legegyszerűbb talán ha a baloldali kifejezést tényezőkre bontjuk:
3x2+4xy+y2=3x2+3xy+xy+y2=3x(x+y)+y(x+y)=(3x+y)(x+y).
Mivel p prímszám ezért csak a következőképpen írható fel egész számok szorzataként:
1.p, p.1, (-1).(-p), (-p).(-1).
Tehát négy egyenletrendszert kell megoldanunk:
3x+y=1,x+y=p vagy 3x+y=p,x+y=1, 3x+y=-1,x+y=-p vagy 3x+y=-p,x+y=-1, ahonnan kapjuk a megoldáspárokat:
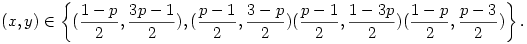
|
| Előzmény: [1867] Mhari, 2007-02-04 20:28:38 |
|
| [1869] Lóczi Lajos | 2007-02-04 21:17:47 |
 A megoldás:
Fejezzük ki a 3x2+4xy+y2=p egyenletből y-t a másodfokú egyenlet megoldóképletével. A gyökjel alatt x2+p áll, melynek nyilván teljes négyzetnek kell lennie, tehát valamely t egész számmal x2+p=t2. Itt p-re rendezve és faktorizálva kapjuk, hogy
1. t-x=1 és t+x=p
vagy
2. t-x=-1 és t+x=-p
3. t-x=p és t+x=1
4. t-x=-p és t+x=-1, amivel megoldottuk a kérdést.
|
| Előzmény: [1868] Lóczi Lajos, 2007-02-04 20:58:25 |
|



 (0,1) Ha ak
(0,1) Ha ak n
n 0 úgy hogy an=1-bn. Írhatjuk:
0 úgy hogy an=1-bn. Írhatjuk:  bn+1=bn(1-bn)2 ezért
bn+1=bn(1-bn)2 ezért 




 (a)-val az "a" szám utolsó,
(a)-val az "a" szám utolsó,  (a)-val az "a" szám utolsó elötti számjegyét. Akkor
(a)-val az "a" szám utolsó elötti számjegyét. Akkor 
 >0 számot, és legyen N(
>0 számot, és legyen N( 1, akkor jobb oldal 1, a bal pedig
1, akkor jobb oldal 1, a bal pedig  .
.