|
| [1943] Csimby | 2007-03-11 13:39:10 |
 309.feladat Van e olyan valós szám amelynek bármely egész számrendszerben felírt alakjában minden számjegy szerepel legalább egyszer.
310.feladat Igaz-e, hogy additív halmazfüggvények szorzata is additív?
Amúgy nincs kedvetek visszatérni a feladatok sorszámozásához? Szerintem az olyan jól bejött eddig...
|
|
|
| [1941] Lóczi Lajos | 2007-03-10 18:10:09 |
 Elképzelhető, hogy mi nem tudjuk megoldani a feladatot, mert nehéz; azért írtam be csak, mert meglepően egyszerű s szép a végeredménye. Inkább sejtsük meg numerikusan, vagy keressük meg az interneten az értékét, illetve, hogy ki az, aki rátalált erre a formulára. (Bár azt is el tudom képzelni, hogy igazából nem is számít, hogy pontosan prímekről van benne szó, és esetleg elég lenne egy alsó/felső becslés az n-edik prímszámra, és abból is ugyanaz az érték jönne ki?)
|
| Előzmény: [1940] Cckek, 2007-03-10 17:25:37 |
|
|
| [1939] Lóczi Lajos | 2007-03-09 23:53:09 |
 Jelölje pn az n-edik prímszámot.
Határozzuk meg a 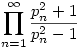 végtelen szorzat értékét. végtelen szorzat értékét.
|
|
|
|
|
|
|
| [1933] Doom | 2007-03-06 07:29:59 |
 Legutóbb rossz helyre tettem, remélem itt már jó...
Egy 'a' oldalú szabályos háromszög minden csúcsában 1-1 kutya áll (A, B és C), majd egyszerre elkezdenek futni egymás felé azonos sebességgel: A B felé, B C felé és C pedig A irányában. Mennyi idő múlva találkoznak?
Segítségként egy "sejtés": egy furcsa "spirál-alakot" megtéve a háromszög középpontjában fognak találkozni, mégpedig egyszerre.
|
|
| [1932] Cckek | 2007-03-01 23:37:51 |
 Így sem érthető teljesen, és nem is tudom, hogyan lehetne ezt helyesen megfogalmazni, de abban az esetben ha n=ab, amit egy egyenlőtlenség helytelen alkalmazásával kapunk!!
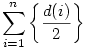 , jön ki, ahol {x} az x , jön ki, ahol {x} az x R törtrészét jelöli. Erre gondoltál?? R törtrészét jelöli. Erre gondoltál??
|
| Előzmény: [1930] S.Ákos, 2007-02-28 16:02:40 |
|
|
| [1930] S.Ákos | 2007-02-28 16:02:40 |
 Elnézést kérek az érthetelenségért és a lassú reagálásért
1) n Z+ Z+
2) az ai-k [a,b] intervallum beli valós számok, és föggetlenül választásuktól reciprokösszegük is [a,b]-beli valós szám lesz
3) ha n db valós számot választasz ki, lehetséges, hogy lesz több olyan [a,b] intervallum, amelyre teljesül 2),  (n) ezek számát jelöli egy adott n-hez (n) ezek számát jelöli egy adott n-hez
És a feladat helyesen: Határozzuk meg ![\sum_{i=1}^n\varepsilon(i)-\bigg[\frac{d(i)}2\bigg]](keplet.cgi?k=F5E4CF8B69D417E5) pontos értékét!-Remélem, így érthetőbb pontos értékét!-Remélem, így érthetőbb
|
| Előzmény: [1922] jenei.attila, 2007-02-26 20:16:10 |
|
|
|
|
|
| [1925] nadorp | 2007-02-26 21:39:15 |
 Szia Cckek !
Kicsit gyorsan reagáltál :-), de azért egy heurisztikát én is vázolnék ( nem bizonyítás, de szerintem befejezhető, a Te megoldásod viszont teljesen korrekt)
Legyen 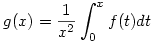 (x>0). Ekkor (x>0). Ekkor
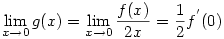 . Tehát . Tehát
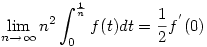 . A kérdéses szumma éppen a balodalnak egy integrálközelítő összege. . A kérdéses szumma éppen a balodalnak egy integrálközelítő összege.
|
| Előzmény: [1923] Cckek, 2007-02-26 20:25:22 |
|
|
|
| [1922] jenei.attila | 2007-02-26 20:16:10 |
 Ákos ne haragudj, de ez teljesen értelmetlen amit írsz. Próbáld meg légyszíves világosabban megfogalmazni. Pl. Mi az n, mi köze a reciprok összegnek az az ai-khez rendelt valós számokhoz (talán az ai-k maguk [a,b] intervallumbeli valós számok? Egyáltalán mik az ai-k)és mit jelent a "jelölje az n-hez tartozó intervallumok számát  (n)" mondat? (n)" mondat?
|
| Előzmény: [1918] S.Ákos, 2007-02-25 19:24:35 |
|
|
|









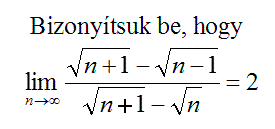

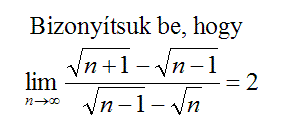

 R törtrészét jelöli. Erre gondoltál??
R törtrészét jelöli. Erre gondoltál?? (n) ezek számát jelöli egy adott n-hez
(n) ezek számát jelöli egy adott n-hez